吸力錨基礎在黏土中的貫入特性
周 密,周樹津,張文耀,薛孌鸞
吸力錨基礎在黏土中的貫入特性
周 密1,2,周樹津1,2,張文耀3,薛孌鸞1,2
(華南理工大學1. 亞熱帶建筑科學國家重點實驗室 / 2. 華南巖土研究院,廣東 廣州 510640;3. 廣州打撈局,廣東 廣州 510260)
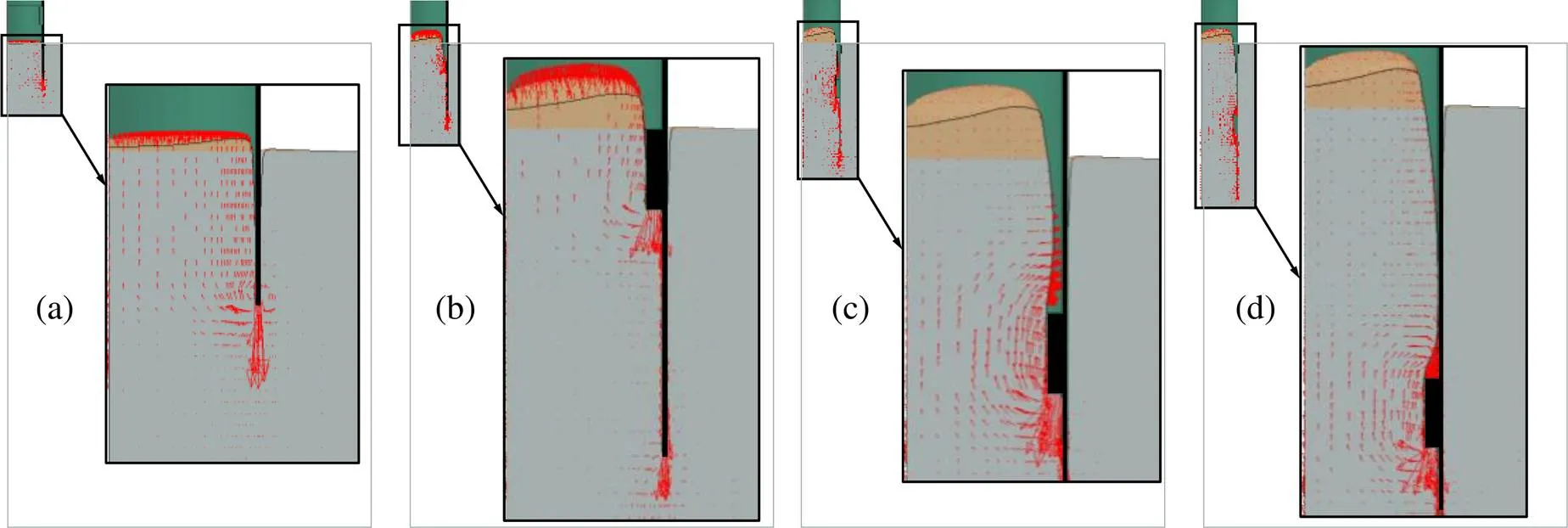
【】研究帶有局部加勁肋的吸力錨基礎在黏土中的貫入特性。利用大變形有限元中的耦合歐拉-拉格朗日(CEL)方法,研究土體硬化軟化效應、加勁肋的尺寸以及土體的參數對吸力錨貫入土體失效機理的影響。對大量數值仿真結果進行統計,獲得在海洋地基中吸力錨基礎沉樁時的土體流動特性,在加勁肋進入土體之后,加勁肋底部受擠壓的土體繞過加勁肋垂直向上流到表面。隨著貫入深度增加,加勁肋上方的土體的開始回流進空腔內(r),底部土體也繞過加勁肋發生旋轉回流。當上部土體完全回流后,在回流的土體表面到原來的地表之間形成一定高度的空腔(c)。定量化評估了局部加勁肋對錨基礎貫入時的土體流動機制的影響,得到加勁肋上部土體旋轉回流高度和完全回流時形成的空腔高度的計算公式,據此能夠準確了解其貫入機理。
吸力錨;沉樁貫入;CEL;土體流動
由于近海空間資源有限,海洋產業逐漸從近海向深水和超深水海域發展[1]。海上風電以及石油平臺的基礎結構形式伴隨水深變化,從固定式支撐結構到漂浮式支撐結構演變。吸力錨基礎,亦稱作吸力桶、沉箱基礎,是一種上部封閉、底端開口的鋼筒結構。與傳統樁基礎相比,吸力錨基礎的豎向、水平向承載力更大,有著更強的抗傾覆能力,能承受較大的上升系泊載荷[2]。吸力錨外壁殼體中包含有板眼部分,系泊鏈附著在板眼上。由于吸力錨基礎的筒壁很薄(直徑與厚度的比值在60到200之間)[3],在上拔的錨固力作用下可能發生局部變形破壞。為避免吸力錨在較大系泊荷載下應力集中導致基礎失效,常在板眼處局部加厚筒壁[4]。根據Randolph等[5]的研究,為優化錨固系泊力,系泊鏈的附著點通常位于總樁長的50% ~ 70%的深度。
在實際工程中,加勁肋常見形式包括沿內壁間隔布置的水平環向加勁肋[5-7],板眼局部增厚環向加勁肋[8-9],板眼處設置加強板(橫向支撐板)[10-11],以及用于重力式基礎平臺的豎向T型加勁肋[12]等。對于帶有水平環向加勁肋的吸力錨,在加勁肋接觸到土體時,樁內土體是否會回流以及何時回流,對于貫入阻力和土塞高度的預測都有很大影響。為研究加勁肋對吸力錨貫入特性的影響,國內外學者開展許多研究,主要是通過離心機試驗[4,13-15]和數值計算[16-17]。Hossain等[4]對兩塊帶加勁肋的板進行離心機試驗,板的一側緊靠透明玻璃箱,采用粒子圖像測速(PIV)技術對位移矢量進行量化,可直觀揭示加勁肋周圍土體的流動形態。Wang等[17]和Zhou等[16]利用網格重劃分和插值技術(RITSS)進行大變形有限元數值模擬,研究加勁肋沉箱基礎的貫入特性。
本研究通過大變形有限元耦合歐拉-拉格朗日(CEL)方法模擬吸力錨靜壓貫入的施工過程,分析吸力錨基礎板眼局部增厚(單個環向加勁肋)對貫入特性的影響。在大變形有限元分析基礎上,對不同加勁肋尺寸、貫入深度、黏土抗剪強度以及應變軟化參數進行參數分析,闡述吸力錨貫入過程的土體流動機理以及它的近似表達式,以期為工程實踐提供理論基礎。
1 數值模型
1.1 CEL方法
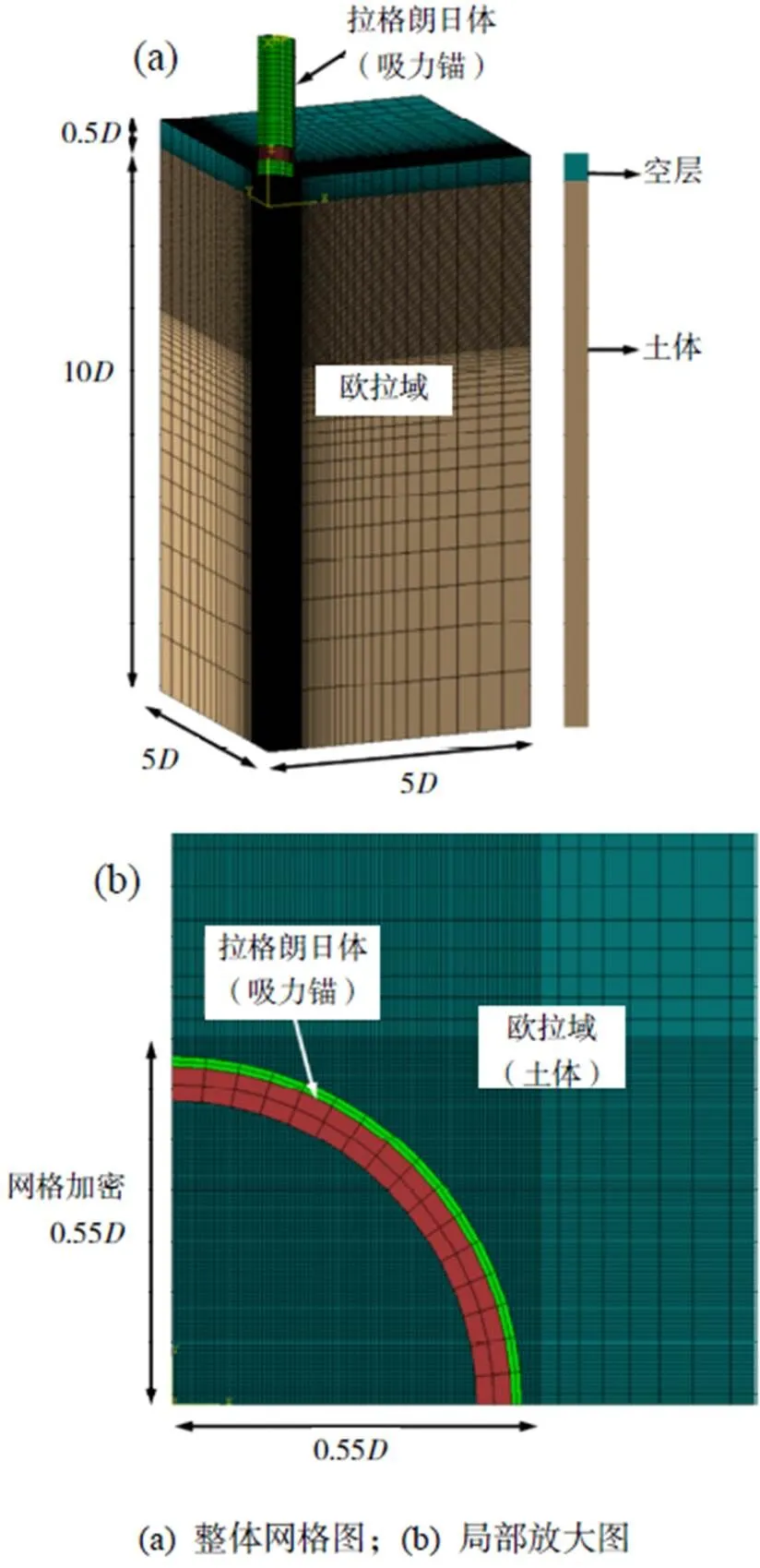
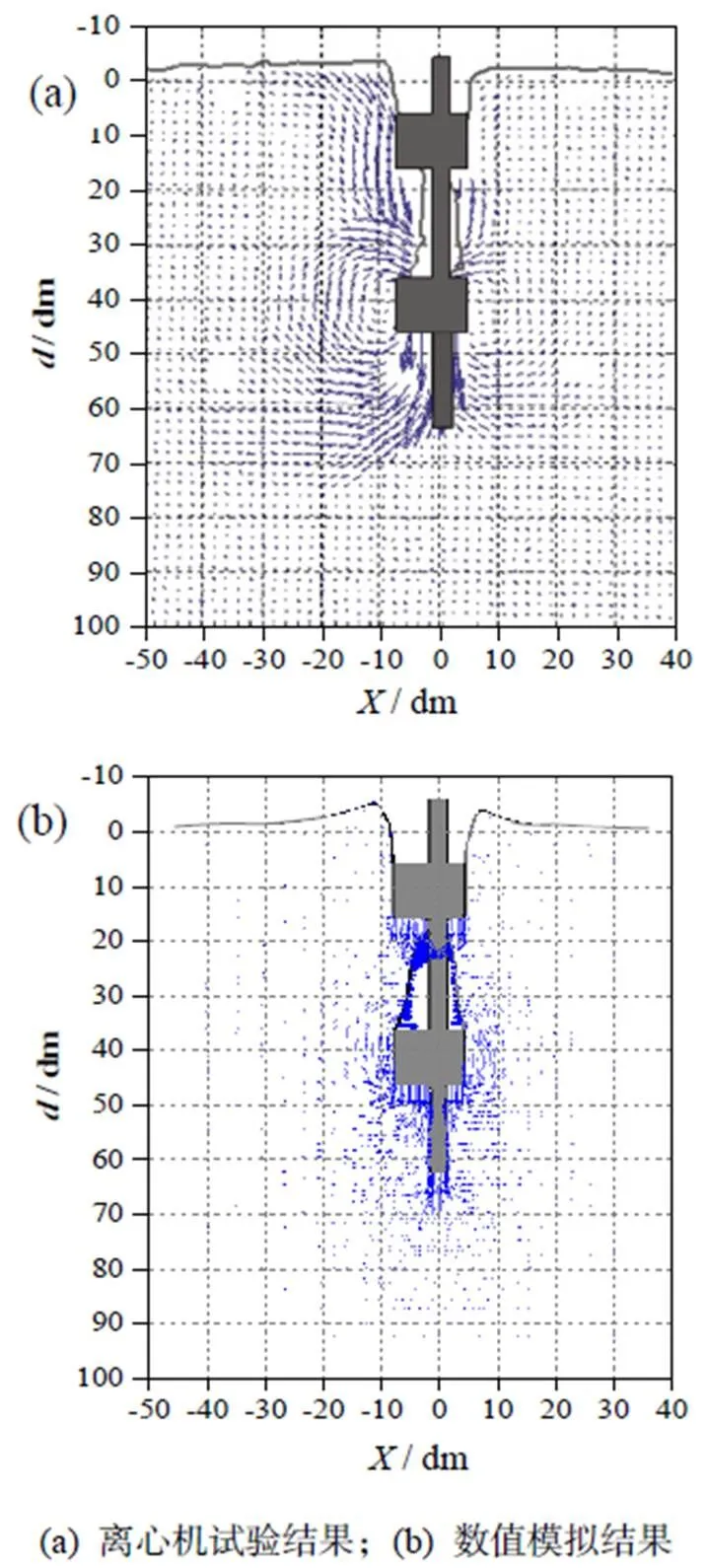
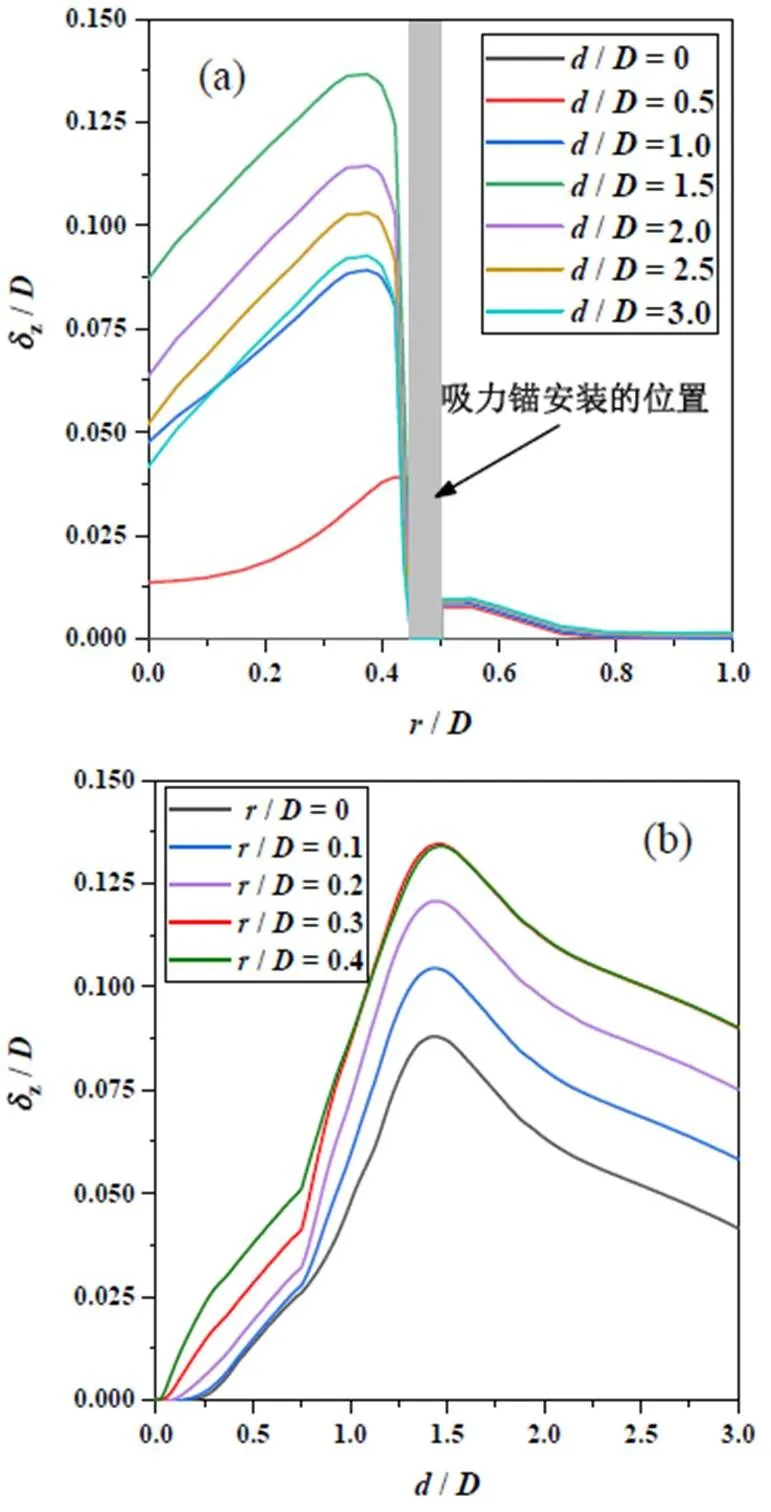
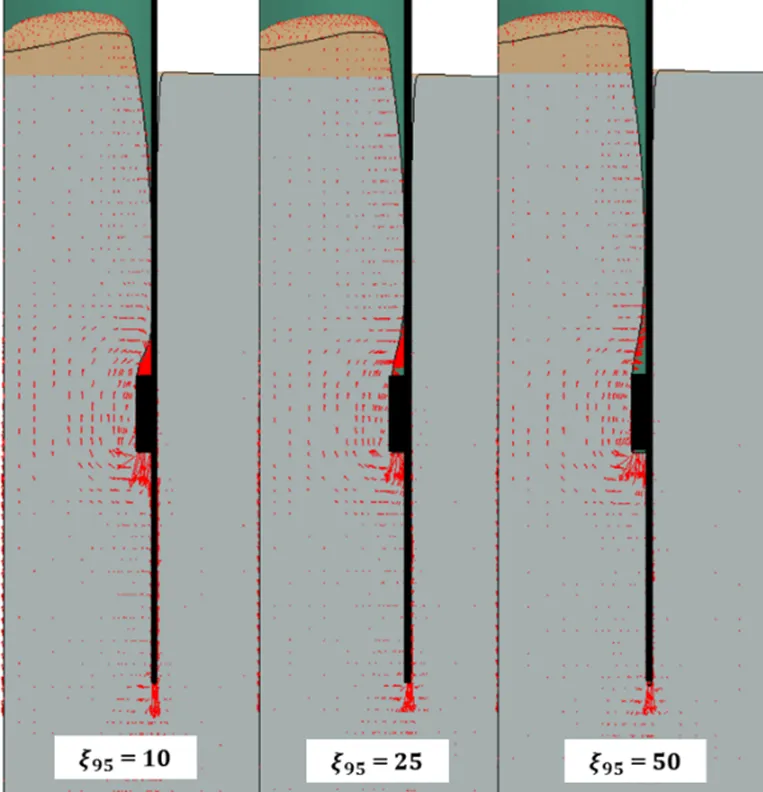
在數值軟件Abaqus/Explicit[18]中使用耦合歐拉-拉格朗日(CEL)方法,基于顯式積分進行大變形有限元分析。在有限元模型中,吸力錨基礎定義為拉格朗日體,土體定義為歐拉體,通過計算每個單元中的歐拉體積分數(E),可以跟蹤歐拉材料(土體)在流過固定歐拉網格時的情況。歐拉單元可以完全被材料填充(E= 1),部分填充(0 在吸力錨貫入黏土過程中,高應變率會引起周圍土體剪切強度增大(稱為土體率效應),同時,土體擾動(即應變軟化)會導致土體抗剪強度降低。Einav等[19]提出應變軟化模型可有效考慮黏土的不排水剪切強度的演化,該模型服從Tresca準則,同時能夠考慮應變率和應變軟化的影響,表達式為 其中,Δ1和Δ3分別為增量Δ間的最大和最小主應變。為當前累積的絕對塑性剪切應變,可按式(3)計算 這種考慮土體軟化和率效應模型已普遍應用于海洋工程問題的數值模擬中[21-23,25]。本研究的數值模型使用Abaqus/Explicit中的用戶子程序VUSDFLD,實現在吸力錨基礎貫入過程中考慮土體軟化和率效應。首先,通過VUFIELD設置一個與網格坐標關聯的場變量,使抗剪強度隨深度變化,作為下一步計算的初始狀態變量。在子程序VUSDFLD中,通過調用應用程序VGETVRM和VSPRINC得到塑性剪切應變分量,計算塑性應變分量的增量以及最大、最小主應變增量,根據式(2)和(3)計算剪切應變速率和累積的絕對塑性剪切應變,然后按式(1)更新土體的剪切強度。 圖1 吸力錨貫入黏土示意 在有限元分析中,為減少計算時間,只對吸力錨基礎和土體取1/4模型進行模擬,長度和寬度為5,深度為10,以避免邊界效應的影響。在樁基礎貫入過程中,在地表上方預留度為0.5的空層,便于考慮土體的隆起(圖2)。土體四周采用法向速度為零的約束條件,底部邊界固定所有方向的速度為零。吸力錨采用帶有8節點拉格朗日單元(C3D8R),而土體的歐拉域是由8節點歐拉單元(EC3D8R)組成。采用基于庫侖摩擦定律的通用接觸算法模擬樁與周圍土體的接觸,罰函數中摩擦系數c取值一般在0.10 ~ 0.42之間[26-28],本研究的有限元模型采用摩擦系數c= 0.20。 土體采用不排水條件下基于Tresca屈服準則的軟土彈塑性本構模型,泊松比= 0.49,模量比/u= 500(為楊氏模量),摩擦角和膨脹角== 0。 地應力平衡通過0= 1(0為側向土壓力系數)施加預應力場與土體自重平衡。在初始地應力平衡步驟后,將吸力錨以恒定速度貫入土中。在顯式動態分析中,貫入速度對計算時間和結果的準確性有很大影響。通過對速度敏感性分析,當吸力錨模擬貫入速度為0.1 m/s,該速度大于實際貫入速度,但是通過參數分析證明該速度不影響計算精度,進而可提高計算效率和獲得較高精度。 圖2 有限元模型 圖3 模型驗證(土體流動機制) 以上模型驗證,表明本研究采用的大變形有限元方法在捕捉土體流動機理和預測貫入阻力的有效性和準確性。 圖4 模型驗證(貫入阻力) (a) 不同位置處的土體隆起;(b) 不同貫入深度的土體隆起 3.2.2 相對延展性系數95的影響 為研究相對延展性系數95對貫入特性的影響,選取相對延展性系數95= 10、25、50等三種情況,具體數值結果見圖7(/= 2)。從圖中可見,相對延展性系數95對土體流動有一定影響。95值不同,在加勁肋上部土體完全回流后,樁內土體表面隆起高度與形態亦不相同。95越大,土體回流越慢,回流后形成的空腔高度越大,這與Hossain等[30]在研究土體應變軟化對紡錘形基礎貫入過程中土體流動的影響規律一致。 d/D = 2 d / D = 1.5 對于非均質軟土,其不排水剪切強度一般隨著土體深度的增加而線性增加。本研究選用Tresca本構模型來對飽和軟黏土進行模擬,土體不排水剪切強度隨深度的線性變化率常用取值范圍為0.5 ~ 2[3,16]。為研究土體抗剪強度對吸力錨貫入特性的影響,本研究選擇三種不同抗剪強度的土體,包括軟弱黏土u0= 1 + 0.5,一般強度黏土u0= 5 +,硬黏土u0= 10 + 2。由圖9可見,土體強度越大,樁芯土和樁底下部土體都受到影響。這是因為土體強度越大,發生剪切破壞時調動的土體越多,流動范圍越大。在貫入深度為/= 1.5時,加勁肋已完全進入土體。當土體剪切強度較低時(u0= 1 + 0.5),樁內土體在加勁肋進入土體時馬上回流,在加勁肋上方土體和樁內壁之間不會形成空腔。當土體泥面剪切強度較高時(u0= 10 + 2),加勁肋上方土體和樁內壁形成空腔,該處的土不會回流到加勁肋和內壁之間的縫隙中,而是垂直向上流到表面。從圖9中可見,當土體強度較大,加勁肋上方土體不回流時,樁芯土的隆起高度要比剪切強度低的土回流時大得多。在貫入深度為/= 2.5時,泥面強度較低的土(u0= 1 + 0.5)完全回流,而當土體剪切強度較高時(u0= 10 + 2),加勁肋底部土體繞加勁肋回流進加勁肋上方間隙,在加勁肋的上表面和樁內壁之間形成一個三角形的空隙。 (a) d / D = 1.5;(b) d / D = 2.5 為研究加勁肋幾何尺寸對吸力錨貫入特性的影響,選取加勁肋高度= 0.5、1.0、2.0 m,加勁肋寬度= 0.1、0.2、0.3 m。圖10(a)顯示,加勁肋高度不同,加勁肋上方土體回流形態基本沒有差別,但是加勁肋下方土體發生旋轉回流的距離不同。加勁肋寬度對吸力錨貫入的土體流動形態的影響見圖10(b),加勁肋寬度越大,樁進入土體的體積越大,樁內因受擠壓而隆起的土體越多;同時,加勁肋寬度越大,加勁肋上部土體越容易發生回流。圖10(b)顯示,當加勁肋寬度較小時(= 0.1 m),加勁肋底部受擠壓的土體主要是向下運動;當加勁肋的寬度較大時(= 0.3 m),加勁肋底部土體受到擠壓,靠近裙壁一側的土體向下運動,遠離裙壁一側的土體繞過加勁肋發生旋轉回流。加勁肋寬度越大,底部受擠壓的土體越多,發生旋轉回流的現象越明顯。 圖10 加勁肋的幾何尺寸對貫入特性的影響 帶單個加勁肋的吸力錨在貫入黏土過程中的土體流動機制見圖11,在加勁肋進入土體后,加勁肋上方土體和內壁之間形成空腔,加勁肋底部受擠壓的土體繞過加勁肋垂直向上流到表面。加勁肋上部土體能保持垂直的最大高度為r(也稱為旋轉回流高度)。隨著貫入深度增加,加勁肋上方土體開始回流進空腔內,底部土體也繞過加勁肋發生旋轉回流。當達到一定深度,上部土體完全回流,在回流土體的表面到原來的地表之間存在一定的高度差,用c表示。 圖11 土體流動機制 有限元計算結果與公式擬合結果對比(圖12),可看到結果基本吻合。 (a) 旋轉回流高度Hr;(b) 完全回流后形成的空腔高度Hc 為研究帶加勁肋的吸力錨基礎貫入海洋黏土過程中土體流動機制,本研究運用耦合歐拉-拉格朗日(CEL)方法模擬吸力錨貫入飽和黏土的過程,分析基礎板眼局部增厚(單個環向加勁肋)對貫入特性的影響,考慮不同加勁肋尺寸、貫入深度、黏土抗剪強度以及應變軟化參數四個影響因素,得出以下結論: 1)加勁肋對吸力錨土體流動機制存在較大影響,貫入前期會在加勁肋上方形成空腔,空腔高度主要受歸一化土體強度影響。 2)土體軟化-硬化參數對土體流動機制存在一定的影響,95越大,土體回流的越慢,回流后形成的空腔高度越大。土體的靈敏度t越大,土體能夠保持垂直的高度越小,越容易發生回流。 3)加勁肋的幾何尺寸對土體流動機制有較大影響。加勁肋尺寸越大,樁內的擠土效應越明顯,土體隆起高度越大。加勁肋的高度對旋轉回流高度以及完全回流后的空腔高度沒有影響,加勁肋的寬度越大,越容易發生回流。 4)擬合出加勁肋上部土體旋轉回流高度和完全回流時形成的空腔高度的計算公式,據此能夠準確了解其貫入機理。 [1] 袁劍平, 毛鴻飛, 潘新祥, 等. 海上浮式風機研究現狀展望——基于南海海域[J]. 廣東海洋大學學報, 2020, 40(5): 133-138. [2] RANDOLPH M F, GAUDIN C, GOURVENEC S M, et al. Recent advances in offshore geotechnics for deep water oil and gas developments[J]. Ocean Engineering, 2011, 38(7): 818-834. [3] CHEN W, RANDOLPH M F. External radial stress changes and axial capacity for suction caissons in soft clay[J]. Géotechnique, 2007, 57(6): 499-511. [4] HOSSAIN M S, LEHANE B M, HU Y, et al. Soil flow mechanisms around and between stiffeners of caissons during installation in clay[J]. Canadian Geotechnical Journal, 2012, 49(4): 442-459. [5] RANDOLPH M F, O'NEILL M P, STEWART D P, et al. Performance of suction anchors in fine-grained calcareous soils[C]// Offshore Technology Conference. Houston, USA, 1998:OTC-8831-MS[2021-06-08]. https://doi.org/10.4043/8831-MS. [6] COLLIAT J L, DENDANI H. Girassol: geotechnical design analyses and installation of the suction anchors[C]// Proceedings of International Conference of Offshore Site Investigation and Geotechnics: Diversity and Sustainability. London, UK, 2002: SUT-OSIG-02-107. https://onepetro.org/SUTOSIG/proceedings-abstract/OSIG02/All-OSIG02/SUT-OSIG-02-107/3220. [7] COLLIAT J L, BOISARD P, GRAMET J C, et al. Design and installation of suction anchor piles at a soft clay site in the gulf of Guinea[C]// Offshore Technology Conference. Houston, USA, 1996: OTC-8150-MS[2021-06-08]. https://doi.org/10.4043/8150-MS. [8] DENDANI H, COLLIAT J L. Girassol: design analysis and installation of the suction anchors[C]// Offshore Technology Conference. Houston, USA, 2002:OTC-14209-MS[2021-06-08]. https://doi.org/10.4043/14209-MS. [9] NEWLIN J A. Suction anchor piles for the Na kika FDS mooring system part 2: installation performance[C]//Inter-national Symposium on Deepwater Mooring Systems. Houston, USA: American Society of Civil Engineers, 2003: 55-75[2021-06-08]. https://doi.org/10.1061/40701(2003)4. [10] COTTRILLl A. Taut legs tested in rig role[J]. Offshore Engineer, 1996, 21(11): 15-17. [11] ERBRICH C, HEFER P. Installation of thesuction piles - A case history[C]// Offshore Technology Conference. Houston, USA, 2002: OTC-14240-MS [2021-06-08]. https://doi.org/10.4043/14240-MS. [12] WATSON P G, HUMPHESON C. Foundation design and installation of the yolla a platform[C]// Proceedings of the 6th International Offshore Site Investigation and Geotechnics Conference: Confronting New Challenges and Sharing Knowledge. London, UK, 2007: 399-412. https://onepetro.org/SUTOSIG/proceedings-abstract/OSIG07/All-OSIG07/SUT-OSIG-07-399/3280. [13] GAUDIN C, O’LOUGHLIN C, HOSSAIN M, et al. Installation of suction caissons in Gulf of Guinea clay[C]// ICPMG2014 - Physical Modelling in Geotechnics. Los Angeles, USA: CRC Press, 2013: 493-499.[2021-06-08]. https://doi.org/10.1201/b16200-67. [14] HOUSE A R, RANDOLPH M F. Installation and pull-out capacity of stiffened suction caissons in cohesive sediments[C]// Proceedings of the International Offshore and Polar Engineering Conference. Stavanger, Norway, 2001: 574-580[2021-06-08]. https://onepetro.org/ISOPEIOPEC/proceedings-abstract/ISOPE01/All-ISOPE01/ISOPE-I-01-212/7963. [15] WESTGATE Z J, TAPPER L, LEHANE B M, et al. Modelling the installation of stiffened caissons in overconsolidated clay[C]//Proceedings of ASME 2009 28th International Conference on Ocean, Offshore and Arctic Engineering, Honolulu, USA, 2009: 119-126[2021-06-08]. https://doi.org/10.1115/OMAE2009-79125. [16] ZHOU M, HOSSAIN M S, HU Y X, et al. Installation of stiffened caissons in nonhomogeneous clays[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2016, 142(2): 04015079. [17] WANG Q, ZHOU X W, ZHOU M, et al. Investigation on the behavior of stiffened caisson installation in uniform clay from large deformation modeling[J]. International Journal of Geomechanics, 2020, 20(9): 04020149. [18] Dassault Systèmes. Abaqus analysis user’s manual[M]. Providence, USA: Dassault Systèmes Simulia Corp., 2016. [19] EINAV I, RANDOLPH M F. Combining upper bound and strain path methods for evaluating penetration resistance[J]. International Journal for Numerical Methods in Engineering, 2005, 63(14): 1991-2016. [20] LUNNE T, BERRE T, ANDERSEN K H, et al. Effects of sample disturbance and consolidation procedures on measured shear strength of soft marine Norwegian clays[J]. Canadian Geotechnical Journal, 2006, 43(7): 726-750. [21] XIAO Z, LU Y M, WANG Y Z, et al. Investigation into the influence of caisson installation process on its capacities in clay[J]. Applied Ocean Research, 2020, 104: 102370. [22] KIM Y H, HOSSAIN M S, WANG D, et al. Numerical investigation of dynamic installation ofanchors in clay[J]. Ocean Engineering, 2015, 108: 820-832. [23] LIU H X, XU K, ZHAO Y B. Numerical investigation on the penetration of gravity installed anchors by a coupled Eulerian-Lagrangian approach[J]. Applied Ocean Research, 2016, 60: 94-108. [24] CHATTERJEE S, MANA D S K, GOURVENEC S, et al. Large-deformation numerical modeling of short-term compression and uplift capacity of offshore shallow foundations[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2014, 140(3): 04013021. [25] ZHOU H, RANDOLPH M F. Resistance of full-flow penetrometers in rate-dependent and strain-softening clay[J]. Géotechnique, 2009, 59(2): 79-86. [26] WANG Y, ZHU X Y, LV Y, et al. Large deformation finite element analysis of the installation of suction caisson in clay[J]. Marine Georesources and Geotechnology, 2018, 36(8): 883-894. [27] CHEN F Q, LIN Y J, DONG Y Z, et al. Numerical investigations of soil plugging effect inside large-diameter, open-ended wind turbine monopiles driven by vibratory hammers[J]. Marine Georesources and Geotechnology, 2020, 38(1): 83-96. [28] 呂陽, 王胤, 楊慶. 吸力式筒形基礎沉貫過程的大變形有限元模擬[J]. 巖土力學, 2015, 36(12): 3615-3624. [29] 盧玉敏. 桶形基礎貫入過程及桶壁貫入效應對基礎穩定性的影響研究[D]. 天津: 天津大學, 2018. [30] HOSSAIN M S, RANDOLPH M F. Effect of strain rate and strain softening on the penetration resistance of spudcan foundations on clay[J]. International Journal of Geomechanics, 2009, 9(3): 122-132. Installation of Suction Caissons in Non-homogeneous Clay ZHOU Mi1,2, ZHOU Shu-jin1,2, ZHANG Wen-yao3, XUE Luan-luan1,2 (1./ 2.,,510640,; 3.,510260,) 【】This study investigated the penetration behavior of stiffened caisson in non-homogeneous clay. 【】Large deformation finite element (LDFE) analysis with the coupled Eulerian-Lagrange (CEL) method was employed to study the effect of stiffener on the soil flow mechanisms. A systematic parametric study was performed to explore the effect of the penetration depth, strain rate and softening parameters, stiffener geometry and soil parameters on the penetration behavior of caisson. 【】 Based on the CEL results, the stiffener has a significant effect on the soil flow mechanisms. At the initial penetration, the soil around the stiffener flows upward to the soil surface. For further penetration, a rotational flow mechanism around the stiffener is developed, with the deformed soil starting to flow back into the gap. Eventually the gap is fully filled, leading to a cavity between the soil surface and the inner skirt. 【】A new soil flow mechanism of stiffened caisson penetration is proposed which quantify the effect of stiffener. The two formulas for predicting the rotational height and critical height have been concluded, which can guide engineers to estimate the failure mechanism of caisson installation. suction caisson; penetration; CEL; soil flow mechanism TS214.2 A 1673-9159(2021)06-0108-10 10.3969/j.issn.1673-9159.2021.06.013 周密,周樹津,張文耀,等. 吸力錨基礎在黏土中的貫入特性[J]. 廣東海洋大學學報,2021,41(6):108-117. 2021-06-08 廣東省基礎與應用基礎研究基金(2021A1515010828) 周密(1983―),男,博士,副教授,主要從事海洋巖土研究。E-mail: zhoumi@scut.edu.com 張文耀(1985―),男,碩士,工程師,主要從事船舶與海洋工程、海上風電前沿施工。E-mail: zwy0401@sina.com1.2 土體軟化和率效應模型

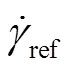


1.3 幾何參數
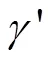
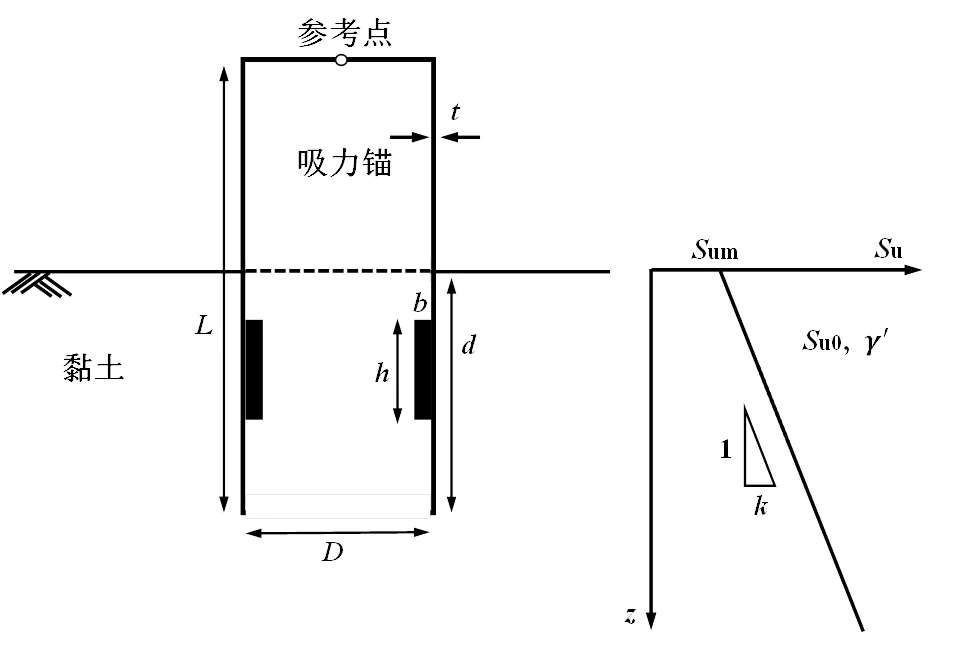
1.4 有限元模型
2 模型驗證
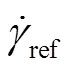
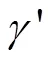

3 結果與分析
3.1 不同貫入深度下的土體流動機制
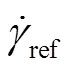
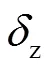
3.2 土體軟化和率效應參數對貫入特性的影響

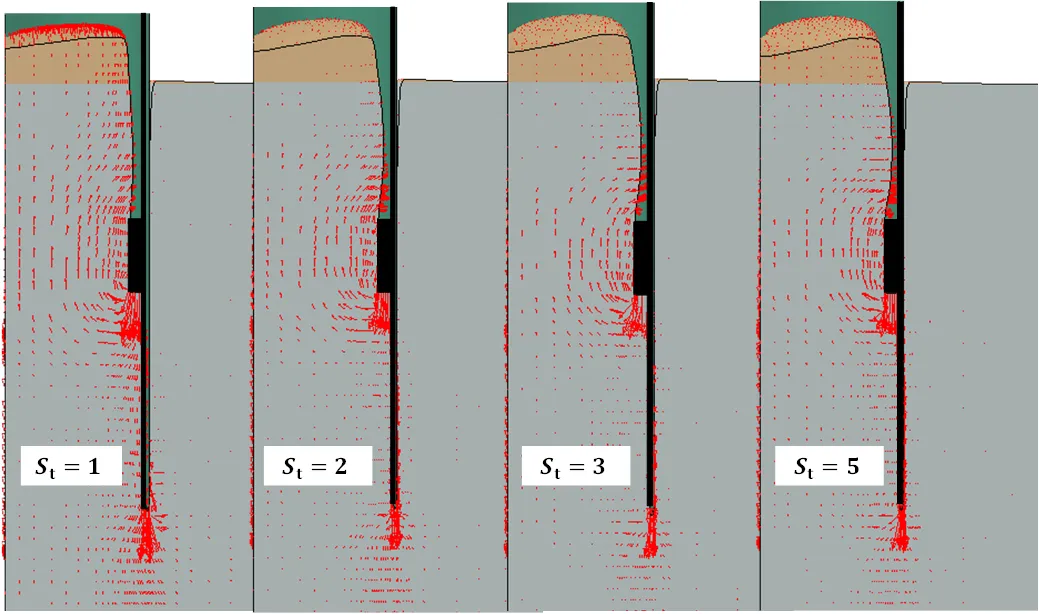
3.3 土體抗剪強度對貫入特性的影響

3.4 加勁肋幾何尺寸對貫入特性的影響

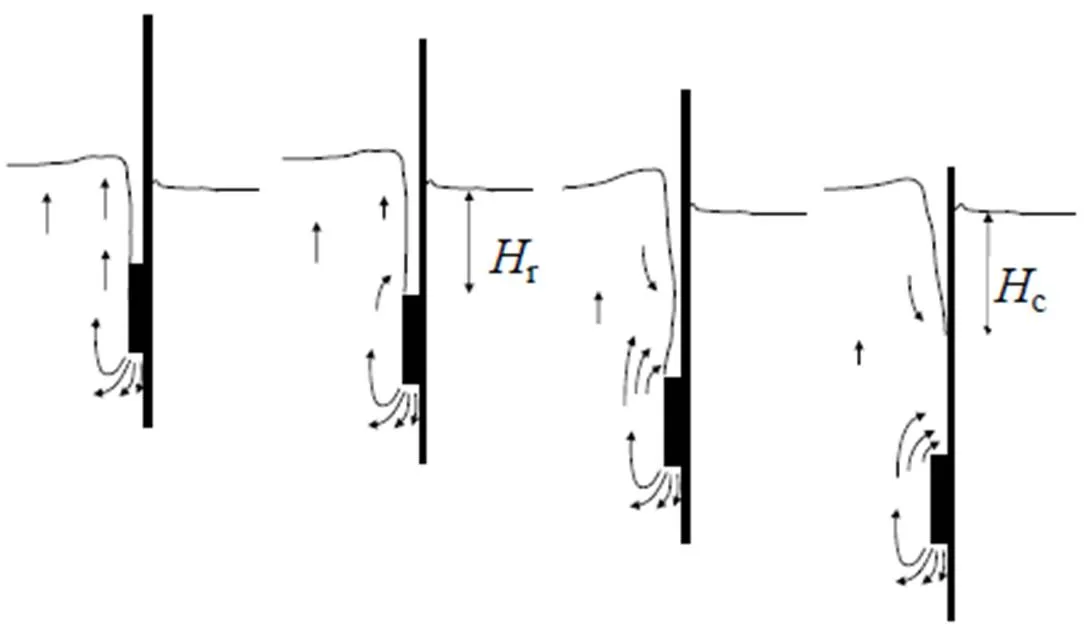
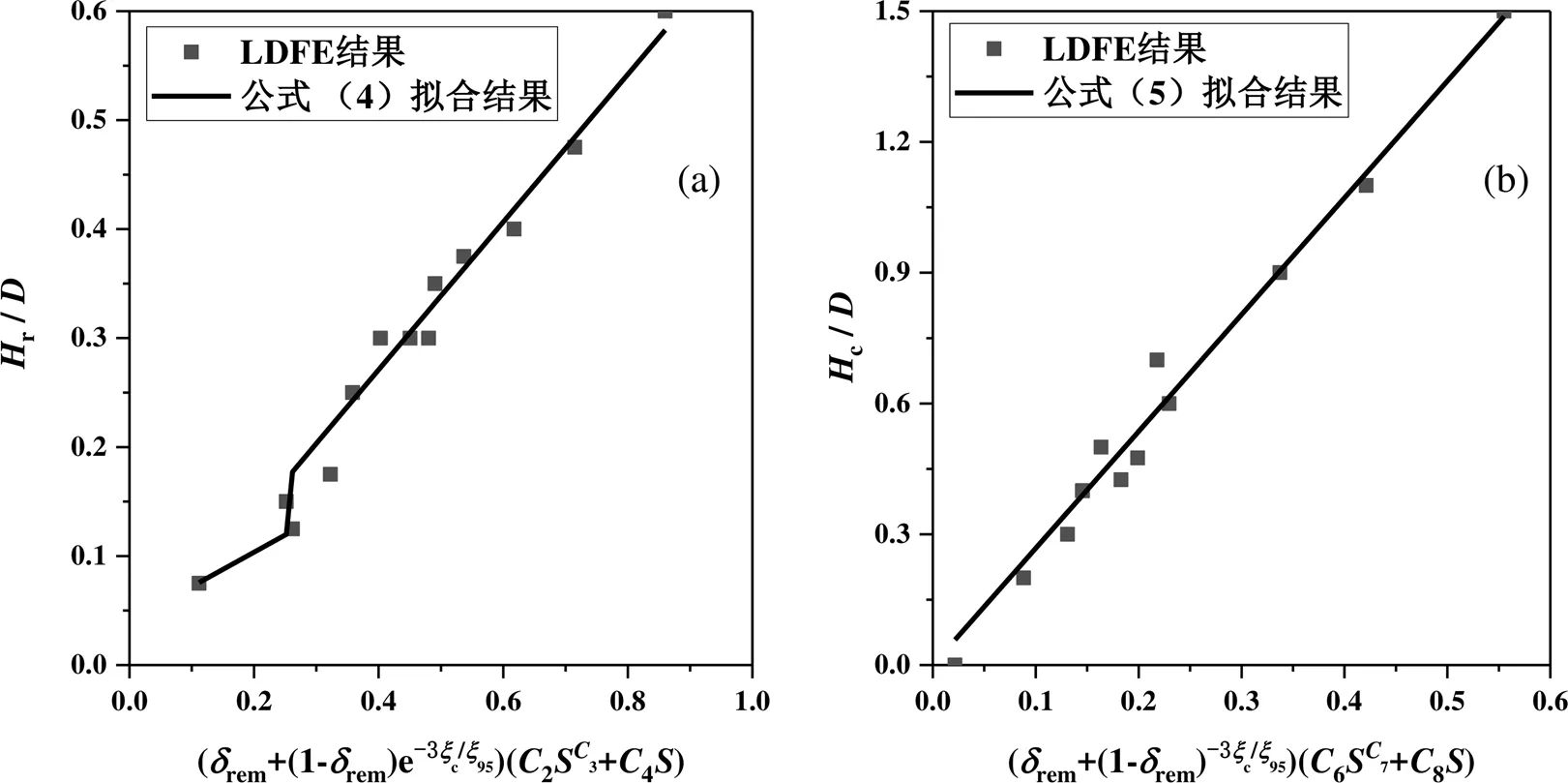
3.5 帶加勁肋吸力錨在貫入過程中的土體回流空腔高度
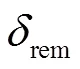
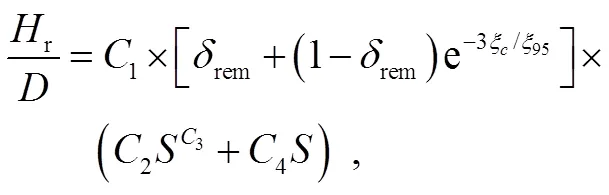
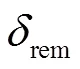
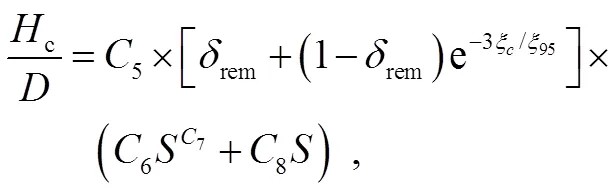
4 結論

