公路隧道中鋼拱架與鋼格柵支護效果對比分析

■夏承明

（三明莆炎高速公路有限責任公司，三明 365000）

鋼架結構是隧道新奧法施工中必不可少的支護結構， 既是臨時支撐也是永久支護結構的一部分，其主要作用是在噴射混凝土未達到設計強度之前或不能及時進行噴混凝土支護位置預先承擔圍巖壓力和約束變形， 提高初期支護系統的抗力，確保洞內施工安全；同時在后期支護中成為永久支護系統的一部分，有利于洞身結構穩定。 鋼架安裝施工快捷，能夠控制圍巖變形，后與錨桿、鋼筋網、噴射混凝土共同作用，協調變形，從而提高初期支護全過程的強度和剛度， 保證隧道開挖的安全性，因此在軟弱破碎圍巖開挖中得到廣泛運用。

鋼架結構主要包括鋼拱架和鋼格柵，但在規范[1]中未對鋼拱架和鋼格柵進行區別， 統稱鋼支撐，但兩者結構形式與工程表現中存在一定的差異，支護效果各有優勢。 相對而言，鋼拱架的剛度較鋼格柵的剛度要大，造價相對也會高。 因此設計施工中，在IV 級圍巖中多采用鋼格柵， 而在V 級圍巖中多采用鋼拱架。

對鋼拱架和鋼格柵各自的力學承載性能，已經有不少研究成果。 對于兩者支護效果的對比分析，也有一些研究成果。 曲海峰等[2]研究了鋼拱架支護形式下的初始釋放荷載規律，其次分析兩種支護結構承載力隨時間的變化規律, 結合實測荷載釋放規律，給出了二者的選擇條件。 但工程中考慮圍巖的流變特征，在技術上存在一定難度，影響了結論的實際應用推廣。 宋元平等[3]把鋼格柵看成鋼筋混凝土結構，經過對比發現鋼筋格柵具備非常優秀的綜合性能,施工方便、經濟,與噴射混凝土結合更好,初期支護質量更能保證等方面的優點, 認為隧道初支應優先選擇采用鋼筋格柵。 王任國等[4]從圍巖變形曲線及支護特征曲線進行研究，認為鋼拱架的剛度大于鋼格柵，所以更有利于協調圍巖變形。

為進一步分析二者的支護效果及經濟技術比，本研究通過有限元計算，首先對鋼拱架和剛格柵分別在相同截面積下的支護效果進行了對比，然后進一步對鋼拱架在局部脫空的支護性能進行研究，為兩種支護形式的方案比選提供參考。

1 有限元模型的建立

1.1 隧道的有限元模型

以莆炎高速公路典型雙車道隧道深埋段的Ⅴ級圍巖的典型斷面為研究對象，建立有限元計算模型，依據荷載結構法進行數值模擬計算。 隧道采用上下臺階法進行分部開挖，跨徑10.74 m，上臺階高度5.37 m。 由于只分析軟弱圍巖段開挖初期的支護效果， 故模擬開挖上臺階階段支護結構的應力應變情況，力學模型示意圖見圖1。 沿隧道縱向取單位長度進行模擬計算，噴射混凝土、鋼拱架、鋼格柵均采用1D 梁單元模擬。 混凝土厚度取30 cm， 彈性模量23 GPa。 采用彈性抗力系數K=200 MPa/m 的徑向彈簧模擬地層反力， 由于土體抗拉強度較小，彈簧考慮僅受壓，兩個拱腳處設置鉸接。 根據規范計算深埋隧道松散荷載垂直均布壓力及水平均布壓力。

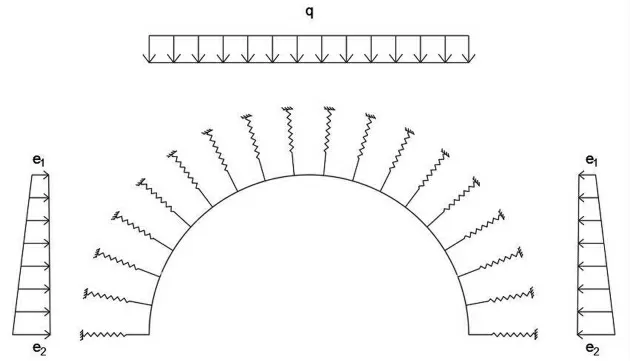
圖1 力學模型示意圖

隧道斷面的計算參數圍巖級別S 為IV、隧道寬度B 為10.74 m、 圍巖重度γ 為22.5 kN·m-3、i 為0.1、ω 為1.57、h 為11.33 m,， 計算豎向荷載q 為254.93 kN/m2，水平向荷載e1為127.46 kN/m2，e2為172.17 kN/m2。 在有限元模型中的計算荷載分布見圖2。

圖2 有限元模型計算荷載分布

1.2 鋼拱架和鋼格柵的計算模型

按設計資料，取鋼拱架模型取結構參數為h 為200 mm、翼緣b 為200、t 為8 mm，單位長度理論質量49.9 kg/m。在同質量情況下設計鋼格柵截面形式和尺寸，采用的鋼格柵布置4 根主筋Υ25，兩根輔筋φ14，鋼筋排布按照剛度最大原則。 兩種鋼架的斷面形式見圖3。 鋼架間距都取0.7 m，根據等效剛度換算法計算兩種模型的剛度， 換算公式為E1I1+E2I2=E1I3，計算得到的結果見表1。

表1 鋼拱架與鋼格柵剛度對比

圖3 兩種鋼架斷面形式

式中E1為混凝土彈模,E2為鋼材彈模,I1為計算模型混凝土慣性矩;I2為鋼架虛線軸慣性矩;I3為等效后的慣性矩;E1I3為等效混凝土的剛度。 取E1=23 GPa；E2=210 GPa[5]。

2 結果與分析

2.1 相同鋼材質量時支護效果對比

由上述計算結果可知，相同質量、相同間距的鋼架時，鋼拱架的剛度大于鋼格柵的剛度。 在荷載作用相同的情況下，根據應力應變關系可知，鋼格柵對應的隧道拱頂沉降在理論上應當大于鋼拱架對應的隧道拱頂下沉。 有限元定量計算結果進一步證實了以上分析。 分別取拱頂沉降和最大水平位移進行比較(表2)，其位移云圖見圖4。 從計算結果可知，鋼格柵支護的拱頂沉降為6.81 mm，鋼拱架支護下為6.24 mm，兩者相差8.4%；鋼格柵支護下圍巖最大水平變形為0.18 mm， 鋼拱架支護下圍巖最大水平變形為0.14 mm，兩者相差22.2%。兩者對比結果表明，在相同的鋼材質量及相同間距下，對于相同圍巖條件，鋼拱架對圍巖變形的控制效果稍優于鋼格柵，但相差不大。

圖4 兩種鋼架主要位移云圖

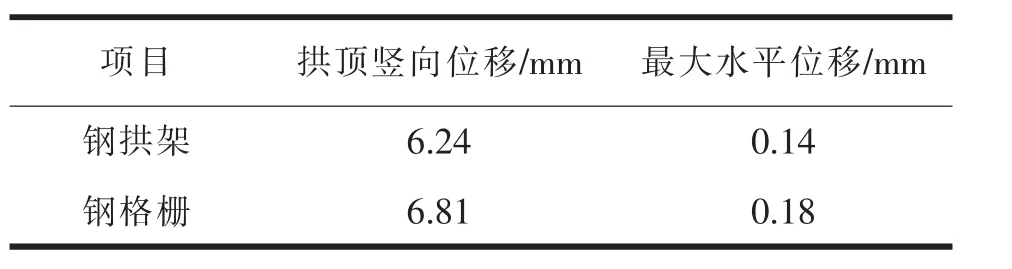
表2 鋼拱架和鋼格柵位移對比

2.2 鋼拱架存在脫空時效果對比

在隧道現場施工中，特別在V 級圍巖中，理想的光面爆破效果相對較難實現，存在大量各種程度的超挖或欠挖現象；即便經過初噴，也很難保證隧道輪廓的平滑； 加之鋼拱架有相對較寬的翼板，鋼拱架翼板和圍巖之間無法緊密接觸；如果噴射不到位會造成混凝土不夠密實， 甚至造成脫空現象，未能與噴射混凝土形成完整的整體，從而成為結構薄弱點，導致整個支護體系的承載能力降低。 而鋼格柵由于其結構特點，噴射混凝土容易穿過鋼筋間的空隙，與圍巖緊密貼合，通常情況下不會出現上述混凝土噴射不密實而導致的脫空現象。

因此，在計算鋼拱架支護的力學效應時，應該進行合理的支護效果折算， 來考慮現場施工中脫空現象造成的影響。 在有限元計算中模擬脫空時，認為該位置不承受圍巖壓力， 按脫空部位長度占拱的周長比例，將脫空部分荷載轉移到其他部位。為簡便起見，取拱頂、拱腰3 處長度各為20 cm 的脫空作為典型工況， 計算分析有脫空時鋼拱架的變形情況。

通過有限元模擬計算，考慮脫空時鋼拱架的位移云圖見圖5，與2.1 節位移結果對比見表3。可知，有脫空時鋼拱架對應的拱頂下沉為8.37 mm， 大于鋼格柵的拱頂下沉6.81 mm， 二者相差約23%；鋼拱架最大水平位移為0.2 mm，大于鋼格柵的水平位移0.18 mm，兩者相差約10%。 上述對比結果表明，當噴射混凝土貼合不緊密造成鋼拱架背后脫空時，其變形量比貼合緊密時顯著增大，且明顯大于鋼格柵的變形量。

圖5 脫空后的鋼拱架主要位移云圖

表3 鋼拱架(有脫空)和鋼格柵位移對比

3 結論

從以上計算對比分析，可以得出以下結論：（1）在鋼材質量相同的條件下， 鋼拱架剛度大于鋼格柵，相應的鋼拱架初支的變形量也小于鋼格柵初支，豎向變形相差8.4%， 兩者相差不顯著； 水平變形相差22.2%， 但在理論條件下絕對值只差只有0.04 mm。（2）考慮鋼拱架背后局部脫空的情形，在拱頂、拱腰各有20 cm 脫空時，鋼拱架初支的變形明顯大于鋼格柵的變形， 特別是豎向變形明顯大于鋼格柵，理論條件下絕對值相差1.44 mm， 差值比例達23%；水平變形值也大于鋼格柵10%。 可見，相同用鋼質量時，鋼拱架的支護效果稍優于鋼格柵；但如果考慮到工程實際，鋼格柵構件間空隙大，噴射混凝土方便，不易造成空洞現象，支護效果明顯優于鋼拱架，反而是更優的選擇。 本研究未考慮鋼格柵的加工費用及時間成本，在實際應用中，可結合現場實際情況綜合考慮。