沖擊荷載作用下非貫通節理巖體細觀破壞模式研究*

董 平，劉婷婷，李新平，丁鹿陽，王 剛

( 武漢理工大學 a.土木工程與建筑學院； b.道路橋梁與結構工程湖北省重點實驗室；c.三亞科教創新園，武漢 430070)

節理作為一種重要地質結構面，將極大影響巖體強度，并且使巖體表現出明顯的不均勻性、 各向異性及不連續性等特征。在外部荷載作用下，諸如工程爆破、盾構施工以及地震等動力作用時，將涉及節理巖體內部應力重分布、應力波透反射及應變率效應等諸多問題，因此節理巖體特性研究具有重要的理論研究意義及工程應用價值。

近年來國內外學者對節理巖體動力響應問題展開了相應研究，如Wu等基于SHPB試驗，研究了動載作用下節理巖體與應力波的相互作用，分析了節理巖體的破壞模式并得到了透射系數的衰減規律[1,2]。馬芹永等探討了軟弱貫通節理砂巖的動態力學特性，發現動態抗壓強度隨節理傾角的增加呈先減小后增大的趨勢，同時，節理試件塑性特征降低，脆性特征增強[3]。薄英鋆等研究了高地應力下節理巖體的破壞模式及動力響應特征，表明相比準靜態計算，動力計算模式下巖體破壞范圍和程度均顯著增大，節理面兩側巖體破壞程度差異顯著[4]。趙怡晴等采用顆粒流軟件研究了加卸載條件下非貫通節理巖體的破壞特性，表明三軸壓縮模擬中，巖橋的破壞以剪切裂紋為主；非線性加載卸圍壓模擬中，巖橋中拉伸裂紋與剪切裂紋分布均勻；卸荷過程中，節理面的剪應力最小[5]。張雨霏等采用改進的SHPB研究了粗糙節理巖體的動態損傷特征，發現節理面的損傷削弱了應力波的透射能力，沖擊荷載作用下節理巖體的損傷主要表現在節理面損傷[6]。Huang等研究了充填厚度對透射系數的影響，發現充填厚度越大，透射系數則越小，同時拉伸應力波不能通過充填節理，反而會將充填節理層撕裂，從而削弱了應力波在充填節理中的多重反射[7]。Dai等對含有初始缺陷的巴西圓盤進行SHPB試驗，得到了加載率與I型斷裂韌度間的關系[8,9]。Li等通過離散元軟件UDEC研究了波在多節理巖體中傳播的規律，認為波傳播取決于巖石節理的力學特性和幾何分布特征[10]。王奇智等對平行雙節理試件進行霍普金森壓桿實驗，研究發現隨著節理傾角從0°至90°變化，試件的動態強度呈現出先增大后減小再增大的變化趨勢[11]。Zou等通過試驗總結了巖石試件在動荷載作用下，裂紋起裂及擴展規律，通過比較節理裂隙的擴展情況，發現動態荷載作用下巖石試件的強度和應變都比在靜荷載作用下大[12,13]。

相關成果對節理巖體力學特性認識及巖體工程發展具有重要意義，但總體而言，節理巖體動力響應研究相對較少，同時，節理巖體破壞實際是能量驅動下細觀構造劣化的過程[14,15]，而目前研究中對細觀響應的分析較為少見，因此，采用離散元軟件PFC2D建立非貫通節理巖體的SHPB沖擊數值仿真模型，從應力波傳播特性、能量轉化、細觀結構劣化特征等多個角度對不同節理角度、貫通率等工況進行數值仿真研究。

1 基于PFC顆粒流的非貫通節理巖體的動態細觀特性數值模型及驗證

1.1 數值模型及參數標定

本次模型的壓桿在滿足應力波測量的基礎上，將入射桿、透射桿長設為2.0 m，直徑設為0.05 m，試件尺寸設計為50 mm×50 mm(寬×高)，為改善應力波傳播能力，降低試樣端部的彌散效應，將入射桿、透射桿顆粒設置為規則排列顆粒，數值模型如圖1所示。

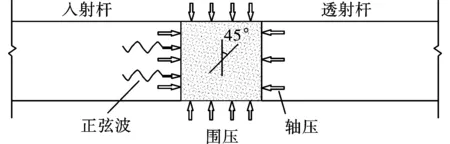
圖 1 SHPB數值模型Fig. 1 SHPB numerical model

顆粒流模型采用線性平行接觸模型(Linearpbond)[16]，通過離散裂隙網格(DFN)圖像反應巖石裂紋演化特征，當顆粒(組)實體與周邊粘結破壞，出現分割裂紋后產生碎塊(Fragment)，即表征巖石破壞產生的碎塊(碎屑)，從而較好反應了巖石類材料的損傷破壞特征。試件中預制的節理采用光滑節理模型(Smooth-joint)[17]，類似形成一系列均勻分布在圓柱截面上的彈簧，很好模擬了一定張開度的節理特性。

為達到模擬初始靜載圍壓效果，采用循環語句生成規則排布的pebble集合體，形成側向clump加載板，通過clump側向板及沖擊壓桿端部直接施加指定力的方式施加初始圍壓(地應力)，進一步通過在入射桿端部施加正弦應力波的方式完成深部節理巖體沖擊仿真過程。試驗中，分別于入射桿和透射桿布置測量圓，用以監測應力、應變等參數。

采用RTX-100巖石三軸儀進行單軸壓縮試驗并對巖石顆粒流模型進行校驗、修正，采用“試湊法”不斷調整模型細觀力學參數[18]，最終獲取花崗巖細觀參數(如表1、表2)。圖2為室內單軸壓縮試驗及相應顆粒流數值模擬應力-應變曲線，兩者較為契合，同時數值試驗中試樣的破壞形態圖與花崗巖試樣破壞形態相似，宏觀力學參數接近，從而驗證了所創建顆粒流模型的可靠性。

表 1 花崗巖模擬試件細觀參數Table 1 Mesoscopic parameters of granite simulated specimens

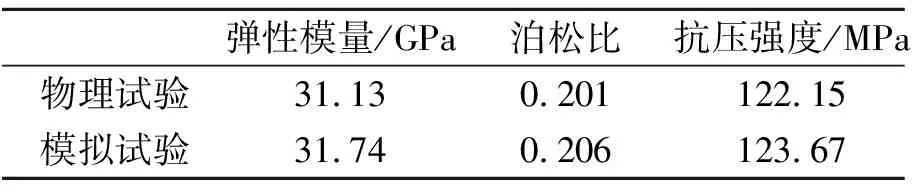
表 2 宏觀力學參數Table 2 Macroscopic mechanical parameters

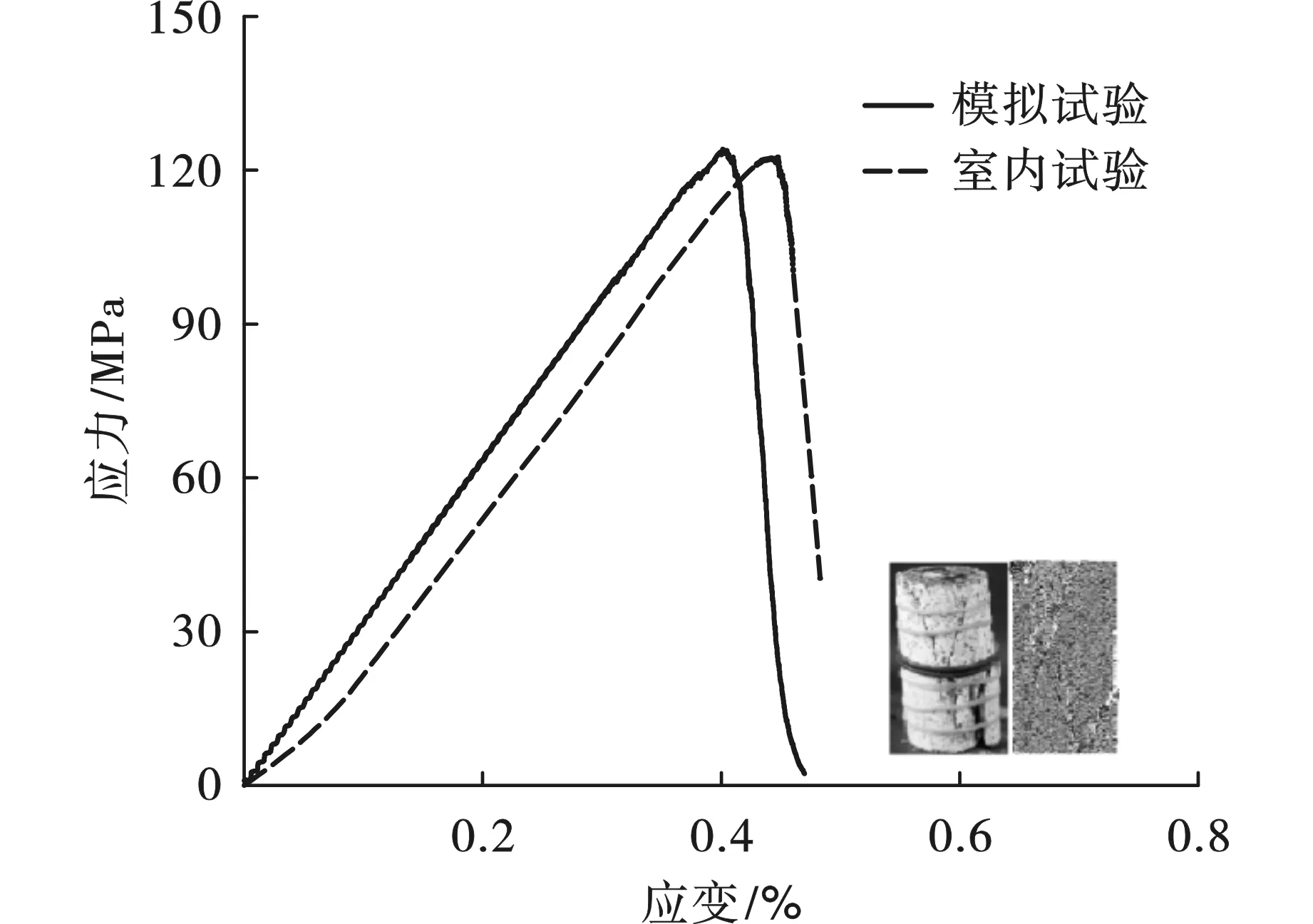
圖 2 應力-應變曲線對比圖Fig. 2 Stress-strain curve comparison graphic

1.2 節理模型及參數

試驗模擬地下100 m應力狀態，考慮自重作用，設置初始圍壓為2.60 MPa，此時假定側壓力系數為1。利用Smooth joint接觸模型改變預置節理處顆粒的粘結方式。為全面了解非貫通節理巖體的動態響應特征，結合模型尺寸設計了系列Ⅰ(節理長度因素)：節理傾角為45°，長度分別為15、20、25、30、35 mm五種不同長度節理試件；系列Ⅱ(節理傾角因素)：節理長度為25 mm，15°、30°、45°、60°與75°五種不同傾角節理試件(見表3)。

表 3 節理試件模擬方案設計Table 3 Simulation scheme design of jointed rock mass

備注：定義水平面為施加沖擊荷載方向，節理傾角為節理面與豎直面夾角。

2 非貫通節理巖體的動態變形特性與細觀破壞模式分析

2.1 節理角度對變形特性和破壞模式的影響

圖3給出了5種不同節理傾角的節理巖體動態應力-應變曲線。從圖上看出全應力-應變曲線總體可分為彈性階段、屈服階段和峰后破壞階段。在彈性階段，應力與應變基本成線性關系，服從胡克定律，表現為彈性特征；在屈服階段，試樣內部損傷加劇，巖石試件局部發生屈服破壞，應力-應變曲線偏離直線，表現出塑性發展特征；在破壞階段，試件內的應力達到其極限承載能力，試件失穩破壞。

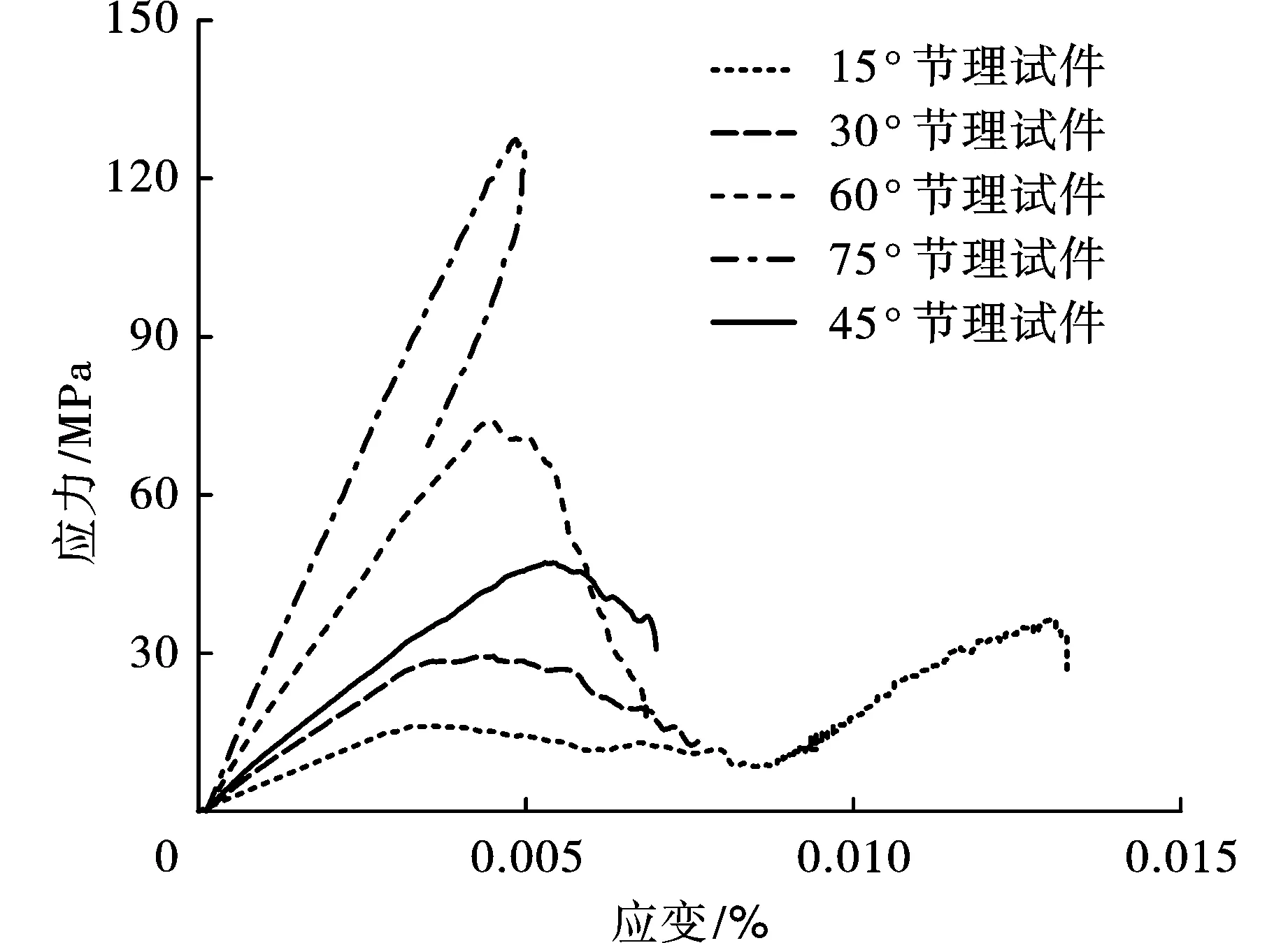
圖 3 不同節理傾角試件應力-應變曲線Fig. 3 Stress-strain curve of specimens with different joint dip angles

節理試樣動彈性模量隨著傾角增加呈增大趨勢，依次為4.4 GPa、8.1 GPa、9.5 GPa、17.6 GPa、27.4 GPa，且動彈性模量差別明顯，最大動彈性模量與最小動彈性模量之間相差可達5倍。其中，對于15°、30°、45°、60°傾角節理試件，當加載臨近峰值強度約80%后，試件進入屈服階段，表現出一定塑性特征；試件進入峰后階段后，變形隨著應力降低而增長，應力-應變曲線呈“開口型”特征。對于75°節理試件，表現出較強的抵抗彈性變形能力，其峰后出現明顯的回彈現象，應力-應變曲線呈“閉口型”，即表明巖石試件仍保持較好的完整性，承載力較大。

不同傾角節理試件動態抗壓強度如圖4所示，當節理傾角由15°增加到75°，節理試件的強度分別為36.5、29.3、47.1、74.2、126.9 MPa，呈近似“V”字型先減小后增大的變化特征。通過應力應變曲線可知，動態荷載作用下，15°節理試件的抗壓強度迅速下降，但由于試件在節理的軸向范圍內，最大程度的保留了完整性，因此，隨著應變的增加，試件能承受更高的軸向應力，并且該殘余強度高于30°節理試件，因而出現曲線“異常”。隨著節理傾角增加，節理對巖石強度弱化能力逐漸降低，試件壓縮強度趨于增大，當節理傾角為75°時，其強度可達126.9 MPa，約為完整試件強度的93.2%。

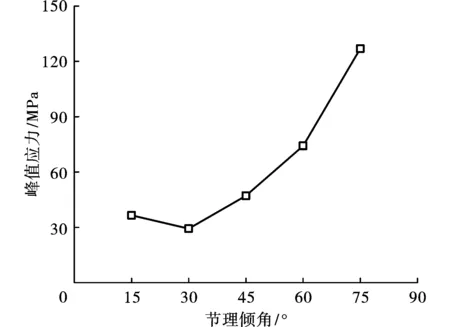
圖 4 峰值應力與傾角關系Fig. 4 Peak stress with different joint dip angles

圖5為不同傾角預制節理巖體受到沖擊荷載作用的破壞過程。當節理傾角小于等于60°時，預制裂紋明顯影響巖石裂紋分布及破壞形態。在360 μs時，節理尖端出現應力集中，并超過臨界應力，造成尖端萌生一定數量裂紋，此時裂紋類型主要為翼裂紋，與最大主應力呈一定角度。當380 μs時，沖擊荷載增大，反翼裂紋與遠場共面裂紋幾乎同時出現并不斷凝聚、擴展，形成局部宏觀裂紋，此時裂紋向最大主應力方向偏轉延伸。當約430 μs時，荷載臨近峰值應力，試件內部裂紋迅速凝聚、擴展，并與預制節理相貫通，發生失穩破壞。對于75°節理試件，預制節理對裂紋擴展影響相對較小，在加載初期，試樣內部不同部位的微缺陷隨機被激活并發展，隨著應力的進一步增加，裂紋出現自相似擴展，且更多的微裂紋被不斷激活，出現宏觀的裂紋交叉并產生局部碎塊、碎屑。由于荷載并未超過試件承載極限，所以裂紋未得以進一步發展，試件仍保持一定完好性。試件最終破壞形態如圖6所示。

不同節理傾角下裂紋信息匯總如圖7所示。隨節理傾角增大，裂紋總數分別為1975、2169、2253、1768、499個，呈先增大后減小的趨勢，這是裂紋擴展區域與巖體初始損傷綜合作用的結果。另外，巖石類材料微破裂可分為張拉裂紋和剪切裂紋，當法向應力超過法向黏結強度時，發生拉伸破壞，對應產生拉裂紋；當切向應力超過切向承載強度時，發生剪切破壞，對應產生剪裂紋，裂紋類型信息極大反應了巖石破壞的本質。這里定義試樣破壞時的剪切微裂紋占總微裂紋的比為剪切破壞比k，剪切破壞比越高表示斷裂過程中剪切破壞作用越明顯，反之表示拉伸破壞作用明顯，從而反映巖石破裂過程中的拉剪斷裂機制。當節理傾角從15°增加到75°，剪切破壞比k分別為0.43、0.40、0.38、0.44、0.49。

2.2 節理長度對變形特性和破壞模式的影響

圖8給出了5種節理長度巖體試件動態應力-應變曲線，隨著節理長度的增加，試件動彈性模量依次為21.6 GPa、14.1 GPa、9.8 GPa、6.7 GPa、5.4 GPa，呈逐漸減小趨勢，最大動彈性模量與最小動彈性模量之間相差可達3倍。其中，對于15 mm節理試件，應力應變曲線在峰后出現回彈現象，即表明巖石試件仍保持較好的完整性，具有一定承載力。當節理長度大于15 mm，試件出現應變軟化現象，應力隨著應變增加而減小，應力-應變曲線整體呈“開口型”特征。

不同長度節理試件動態抗壓強度如圖9所示，可知節理對巖體的強度弱化效應明顯。定義節理長度與試樣沿節理傾角方向總長度的比值為貫通度δ，則當δ由0.21增大到0.50，試件的強度分別為90.1、62.9、47.1、33、20.7 MPa，呈逐漸減小趨勢。節理長度差異表征了不同的巖石初始損傷，預制節理長度越大，試件完整性越差，造成初始損傷越大，如節理長度15 mm試件，其強度為完整試件的67%，較大程度上保留了試件抵抗荷載的能力，而對于節理長度35 mm試件，其強度僅為完整試件的15%，承載能力下降明顯。

根據圖10展示的不同長度預制節理巖體在受到沖擊荷載作用的破壞過程，節理傾角為45°，顯然，當應力波傳播至非貫通節理處時，節理尖端出現了應力集中，造成尖端萌生大量微裂紋，同時試樣內部不同部位出現少量隨機分布裂紋。當節理貫通度較小時(δ=0.21～0.35)，尖端裂紋主要為翼裂紋，與最大主應力呈一定夾角；而當節理貫通度較大時(δ=0.35～0.50)，除節理端部的翼型裂紋外，沿節理方向產生明顯的共面裂紋，并不斷向試件端部擴展。隨著沖擊荷載的增大，短節理試件中除翼型裂紋外，出現一定大量的反翼裂紋與遠場共面裂紋。當約430 μs時，試件內部裂紋迅速凝聚、擴展，短節理試件在反翼裂紋主導下貫通破壞，長節理試件在反翼裂紋和共面裂紋共同作用下，出現宏觀斷裂帶，試件最終破壞形態如圖11所示。

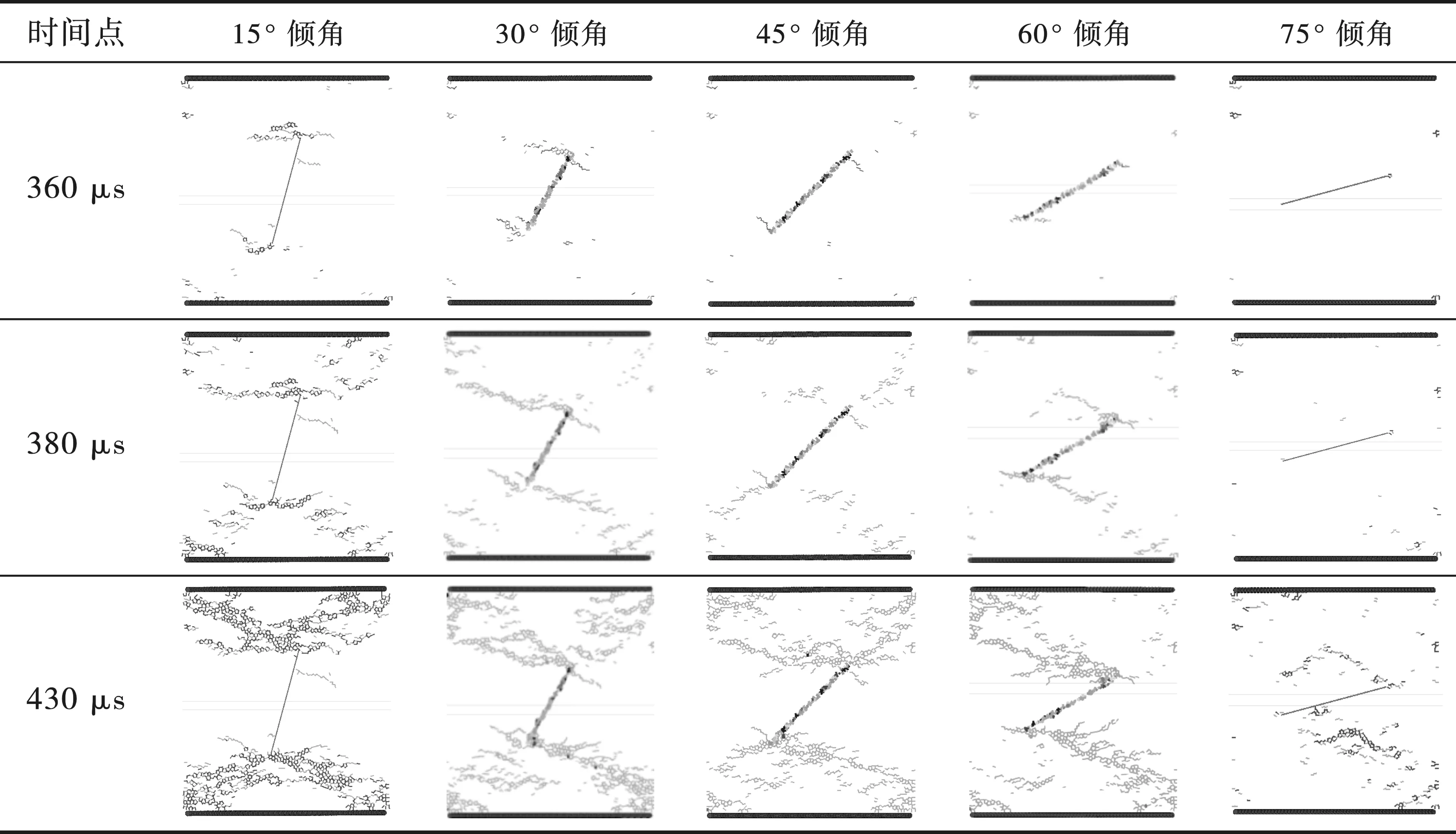
圖 5 不同節理傾角試件裂紋演化圖Fig. 5 Crack propagation of specimens with different joint dip angles

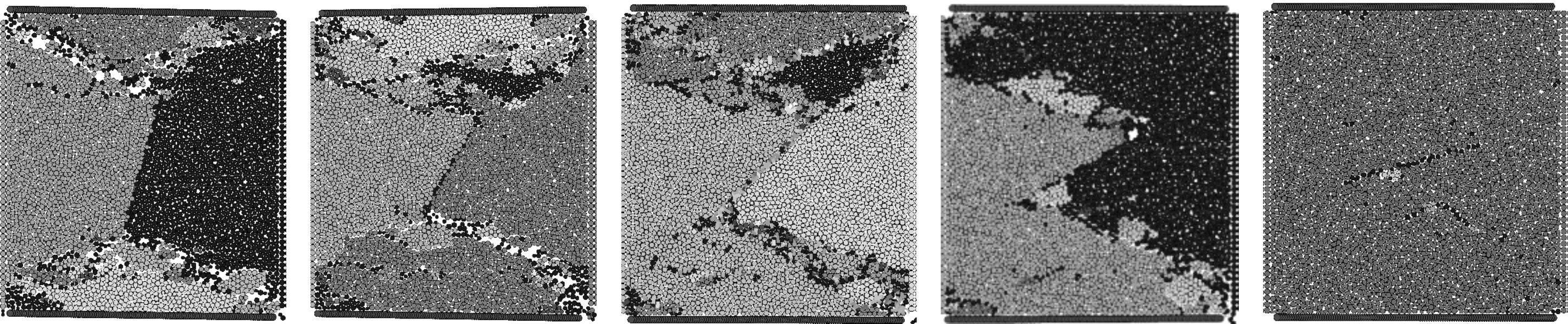
圖 6 不同節理傾角試件破壞形態圖(15°、30°、45°、60°、75°)Fig. 6 Destruction form of specimens with different joint dip angles(15°、30°、45°、60°、75°)

圖 7 生成裂紋數目與節理傾角關系Fig. 7 Change law of the number of cracks with different joint dip angles

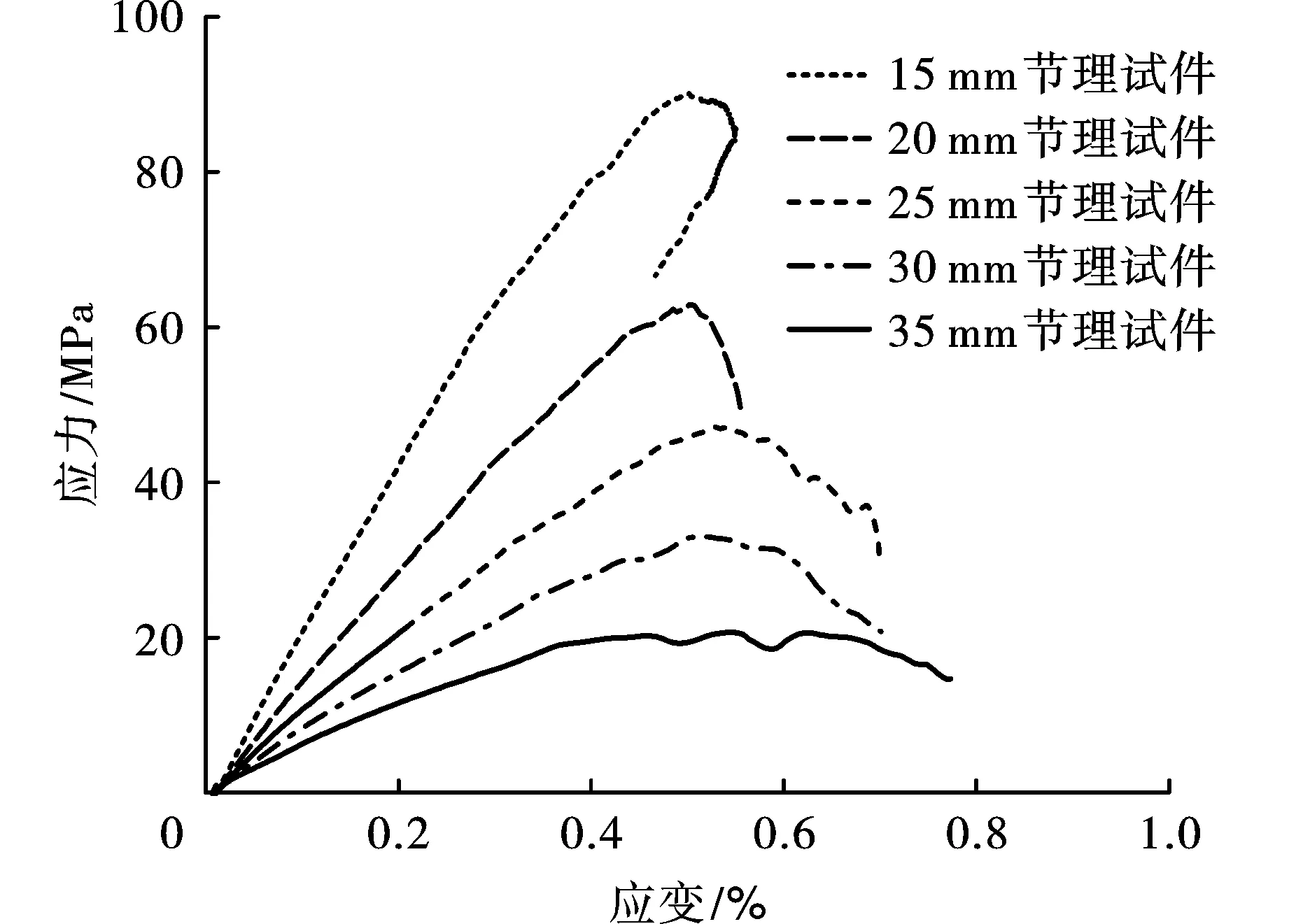
圖 8 不同節理長度試件應力-應變曲線Fig. 8 Stress-strain curve of specimens with different joint length

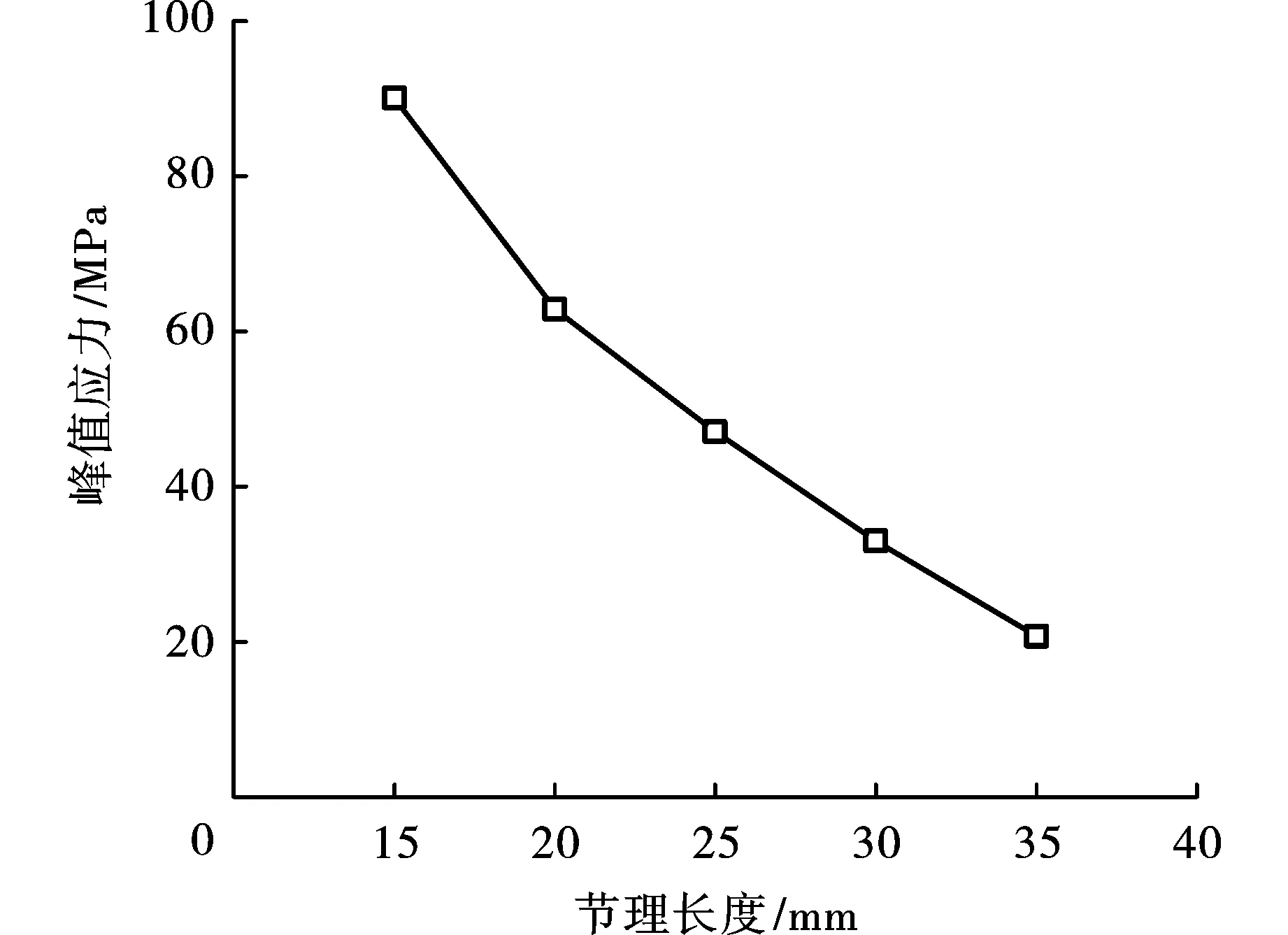
圖 9 動態峰值強度與節理長度關系Fig. 9 Peak stress with different joint length

圖12為裂紋信息匯總統計，隨節理長度增大，裂紋總數分別為1016、1894、2253、2305、1834個，呈先增大后減小的趨勢，其中，對于短節理試件(15～25 mm)，節理長度的增加，促使反翼裂紋大量增加，形成了更寬的破碎帶；當節理長度增加到一定程度，即本文的30～35 mm，共面裂紋產生的優勢主裂紋直接影響了試件裂紋擴展與破壞模式，反翼裂紋作用弱化，對于45°傾角節理試件，最終形成更為明顯的沿節理方向的對角破壞。當裂紋長度由從15 mm增加到35 mm時，剪切破壞比k分別為0.431、0.430、0.390、0.387、0.371，呈逐漸下降趨勢，即隨著節理長度增加，拉伸作用趨于明顯。

圖 10 不同節理長度試件裂紋演化圖Fig. 10 Crack propagation of specimens with different joint length

圖 11 不同節理長度試件破壞模式(15～35 mm)Fig. 11 Destruction form of specimens with different joint length (15～35 mm)

3 節理貫通度對應力波能量衰減規律的影響

為了研究節理的貫通度對應力波衰減規律的影響，定義參數透射系數T為透射波與入射波的波幅比值。25 mm節理試件的入射波、透射波、反射波隨時間的變化關系見圖13。不同貫通度下節理巖體的透射系數如圖14所示，隨著貫通度的增加，透射系數單調減小，應力波衰減明顯，再次說明了節理對巖體強度的弱化作用。

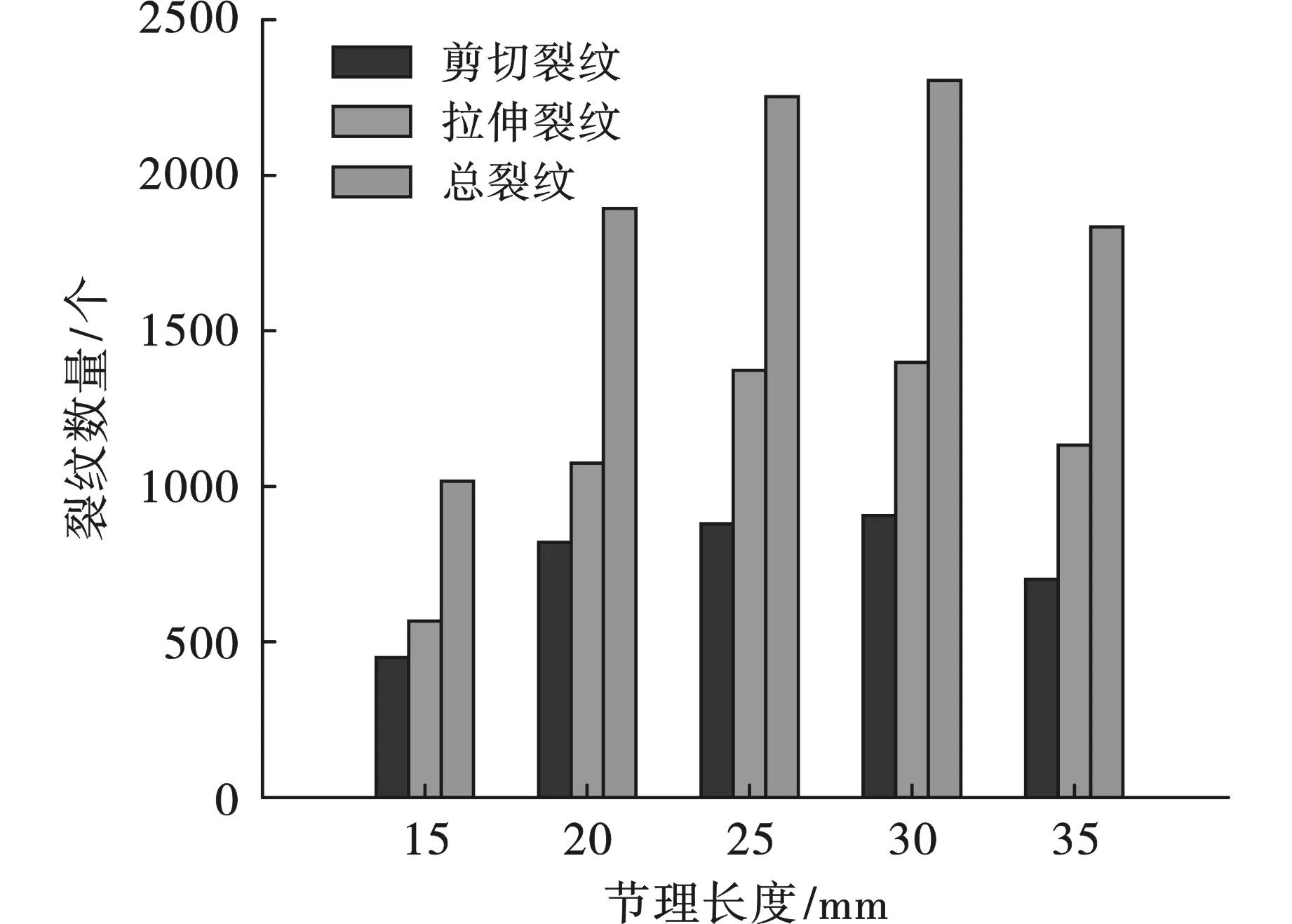
圖 12 裂紋生成數量與節理長度關系Fig. 12 Change law of the number of cracks with different joint length

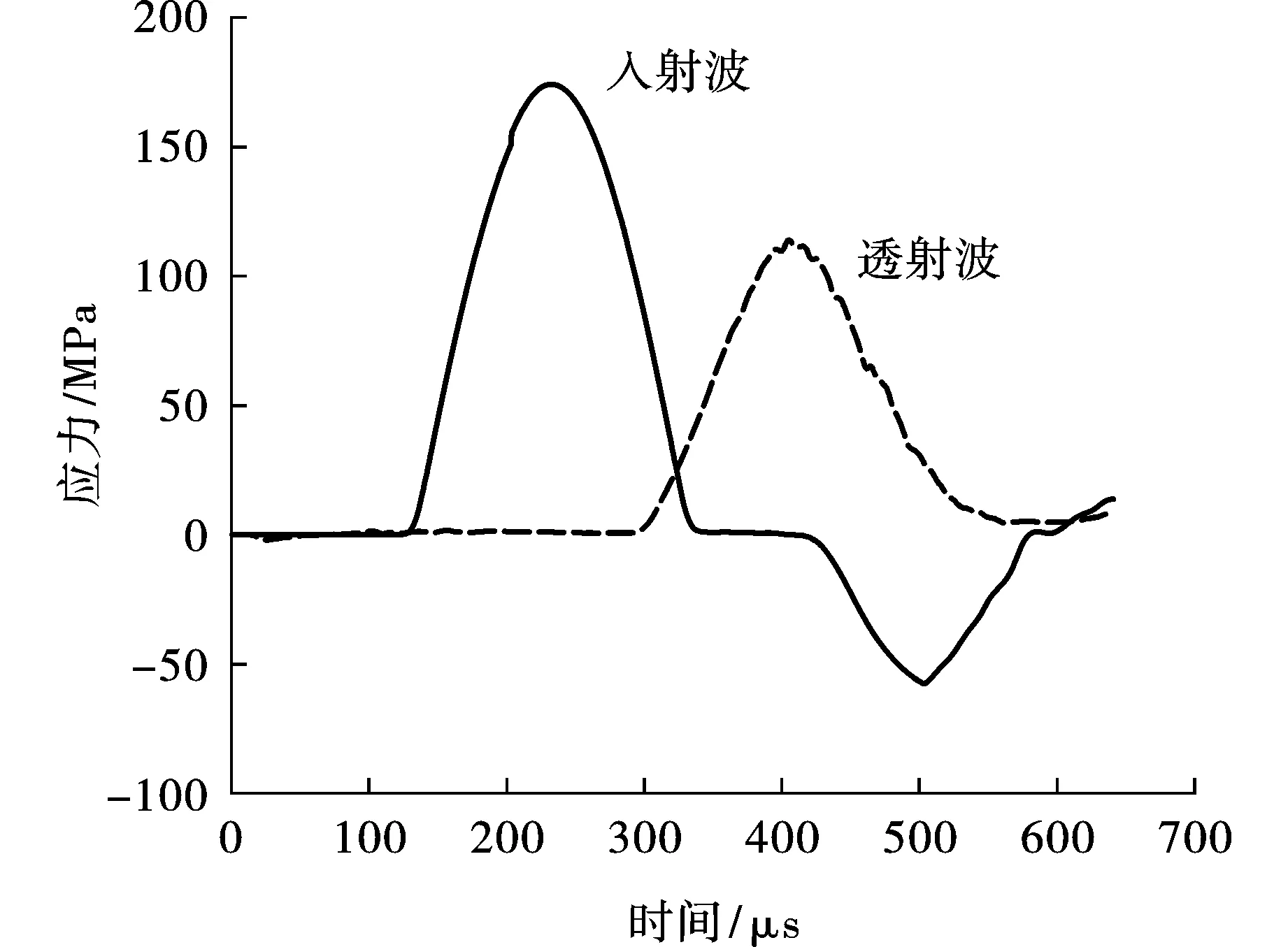
圖 13 25 mm節理試件入射波、透射波、 反射波應力-時間曲線Fig. 13 Stress-time curve of incident wave,transmitted wave and reflected wave of 25 mm joint specimen

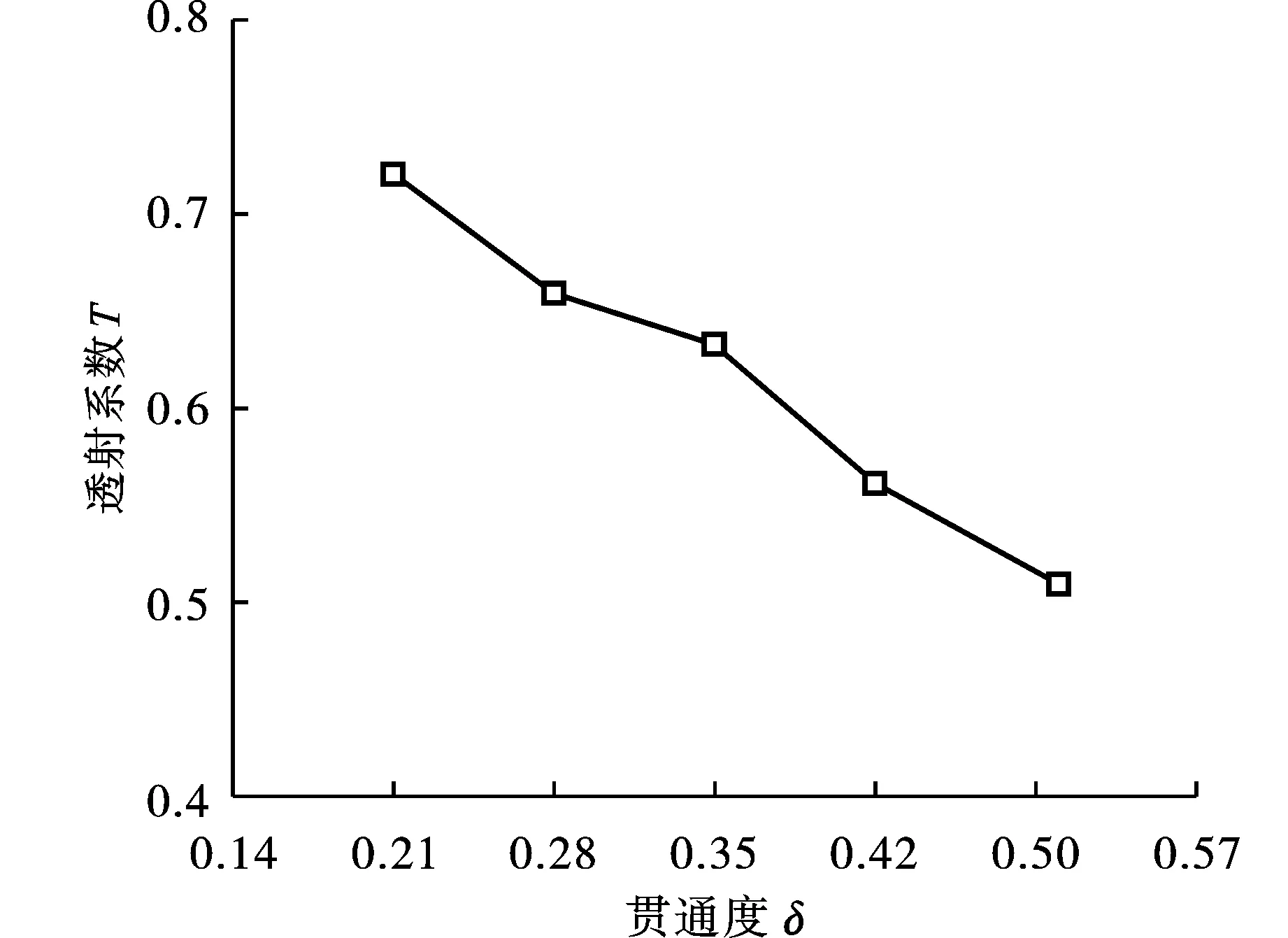
圖 14 透射系數與貫通度關系圖Fig. 14 Transmission coefficient with different joint continuity degree

巖石試件吸收了應力波能量，從而導致內部裂紋擴展貫通，因此對巖石試件在沖擊荷載下的能量耗散特征展開研究，將有助于揭示巖石破壞特征的本質[19]。當應力波傳播到非貫通節理巖體時，入射波EI能量主要會分散為三部分：繼續傳播的透射能ET；反射回去并可能產生拉應力的反射能ER；誘發微裂紋產生擴展甚至貫通的耗散能ED。其計算公式如下[20-22]

(1)

(2)

(3)

式中:A0、ρ0和C0分別為入射桿和透射桿的橫截面面積，初始密度以及彈性波縱波波速；εI(t1)、εR(t1)、εT(t1)分別為入射波，反射波與透射波的時程應變。

定義能量透射系數Te、能量反射系數Re以及能量耗散系數De分別為透射能、反射能及損耗能與入射能的比值。如圖15所示，隨著節理貫通度的增加，能量透射系數迅速減小，能量反射系數增加，能量耗散系數先增加然后趨于穩定，出現減小的趨勢。能量耗散變化規律與圖12中節理裂紋數量結果吻合，隨著節理貫通度的增加，微裂紋數量并不是一直增加，而是快速增加后，增加速度變緩，最后出現減少。因為節理貫通度增加后，節理更容易產生破壞，即新生微裂紋數量較小也可以導致貫通度較高的節理巖體產生破壞，從而導致應力波能量大量被反射，應力波衰減嚴重。

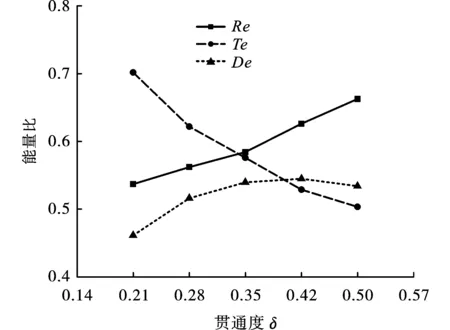
圖 15 各能量系數與貫通度關系圖Fig. 15 Energy ratio with different joint continuity degree

4 結論

采用顆粒流離散元程序(PFC2D)建立了分離式霍普金森壓桿(SHPB)數值模型，從細觀角度研究了含非貫通節理巖體的動態破壞特征及應力波傳播規律，主要結論如下：

(1)沖擊荷載作用下，試件破壞過程可分為彈性階段、屈服階段和峰后破壞階段，節理長度的增加或傾角的減小，均可促使試件應力-應變曲線特征由“閉合型”向“開口型”轉變。

(2)隨節理傾角從15°增加至75°，巖石動態抗壓強度呈現先減小后增大的近“V”字型變化趨勢，裂紋數量呈先增大后減小的變化規律；非貫通節理試件的破壞由剪切與拉伸共同作用導致，其中拉伸作用更加突出。

(3)隨著節理貫通度的增加，巖體初始損傷增大，試件動態抗壓強度逐漸降低。巖石破壞模式由反翼裂紋主導貫通破壞向反翼裂紋和共面裂紋共同破壞轉換。

(4)隨著節理貫通度的增加，能量透射系數減小，能量反射系數增加，能量耗散系數呈現出先增加后減小的變化規律。此外，應力波衰減隨著節理貫通度的增加而趨于明顯。