基于數據分布信息的相關濾波器算法研究

蔣琦，周剛

（四川大學錦江學院計算機學院，眉山 620860）

0 引言

圖像識別與檢測是計算機視覺的重點研究領域，相關濾波器算法因其簡單的實現方法和較優秀的實現效果成為該領域的研究熱點［1］。相關濾波器是利用圖像中目標之間的相關性進行判別，其中相關性指的是圖像信號的相似性，相關濾波器利用一定數量的訓練數據的相關性得到濾波模板，然后通過濾波模板判斷其他圖像中目標與模板的相似程度［2］。因此，相關濾波器最重要的研究內容就是如何得到濾波模板。眾多研究人員提出了大量算法，并取得了不錯的實驗效果。文獻［3］提出了無約束最優權衡綜合判別函數濾波器（unconstrained optimal trade-off synthetic discrimi?nant function，UOTSDF），通過平衡參數優化一個判別函數來得到濾波器。文獻［4］提出了最優權衡綜合判別函數濾波器（optimal trade-off synthetic discriminant function，OTSDF），這種濾波器在思想上與UOTSDF是一致的，不同之處在于有無約束條件。文獻［5］提出了平均合成精確濾波器（av?erage synthetic exact filter，ASEF），先求出單張圖像的弱濾波器，再集合多個弱濾波器求均值得到一個強濾波器；文獻［6］提出了最小輸出誤差平方和濾波器（minimum output sum of squared error，MOSSE），通過高斯函數產生峰值，最小化實際相關輸出與期望輸出誤差的平方和而得到濾波器。文獻［7］改變思路，將支持向量機［8］（support vector machine，SVM）的思想引入相關濾波器，在最大化響應峰值的同時最大化分類間隔，提出了最大間隔相關濾波器（maximum margin correlation filter，MMCF）。MMCF利用了SVM優秀的分類泛化性能，兼顧大間隔原理和最小化樣本均方誤差，使這種相關濾波器相比傳統的相關濾波器在性能上獲得了較大提升。

但是，MMCF在結合SVM的同時，并未考慮到SVM存在的問題。SVM在建立分類超平面時只利用了邊界上的樣本點，忽略了樣本的整體結構信息以及樣本之間的結構聯系，因此所得的超平面并不一定符合樣本實際結構信息，而MMCF也繼承了這個缺點。為了解決上述問題，本文提出兩種方法進行改進，兩種算法都是充分利用樣本數據的結構信息，提高所得訓練模板的識別和檢測效果。

1 相關工作

本節首先簡要介紹SVM，再對相關濾波器和MMCF進行簡要闡述。

1.1 支持向量機

SVM是一種經典的分類算法，在當今計算機視覺領域仍然發揮著重要的作用［9］。SVM提取訓練樣本的特征，在樣本特征空間尋找樣本點的最大間隔，通過建立分類超平面盡量分隔不同類別的樣本，以達到分類的目的。在實際訓練中，SVM的求解其實是使該超平面與任一樣本之間的最小L-2范數距離最大化。設有一數據集為U=則SVM的定義如下：

其中，w是分類超平面法向量，b為偏置量，ξ為松弛變量，T表示轉置，C為懲罰系數，y i為樣本標簽，x i是輸入數據x i的向量形式。SVM在眾多的分類應用中取得了不錯的效果，但仍然存在一些問題，并沒有考慮樣本的結構信息和內在聯系。

1.2 最大間隔相關濾波器

相關濾波器利用模板與目標的相關性進行判別，其主要研究問題為求解出濾波模板w。傳統的相關濾波器可以被看作為優化輸入圖像的理想期望相關輸出與訓練圖像和模板的相關輸出之間的歐式距離［10］。相關濾波器定義為：

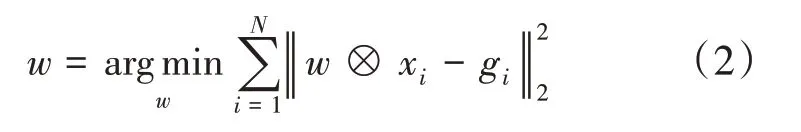
其中，?為互相關運算，g i為期望相關輸出，不同的相關濾波器算法所構建的g i并不相同。

大多數相關濾波器的改進思路都集中于g i的構建上，但改進效果都有一定局限性。文獻［7］將SVM的思想引入相關濾波器，提出了MMCF，進一步提升了相關濾波器的鑒別能力。MMCF的定義為：

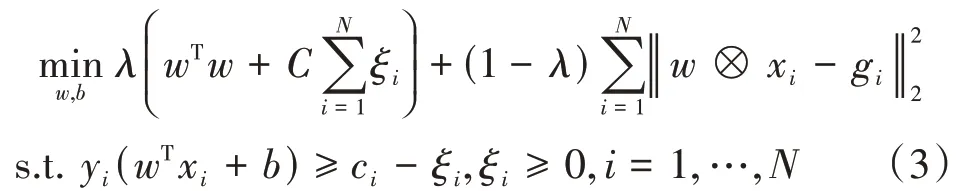
其中，w既是分類超平面法向量，也是濾波模板，λ為平衡系數，用于平衡支持向量部分和相關濾波部分的權重，c是一個與樣本有關的常量。MMCF利用SVM和相關濾波各自的優點，提升了相關濾波器的實驗效果。但同時也繼承了SVM的缺點，樣本的訓練并不充分。

2 算法原理

為了解決MMCF所存在的未利用樣本整體分布信息和樣本內部聯系的問題，本文提出了兩種方法，分別是基于最小類內方差和最小類局部保持方差的相關濾波器。

2.1 基于最小類內方差的相關濾波器

SVM在建立分類超平面時未考慮樣本整體信息，致使MMCF在訓練時同樣存在這個問題。針對SVM這一問題，文獻［11］提出了將Fisher線性判別的思想與SVM結合起來，提出了最小類內方差支持向量機（minimum class variance support vec?tor machine，MCVSVM）。設有一數據集為U={x i||i=1,…N}?Rd×N，且分別屬于兩類{A+,A-}，則MCVSVM的定義如下：

其中，S w為類內散度矩陣，其定義為：

其中，m A是A類樣本的均值。類內散度矩陣用于描述異類樣本的整體分布情況。因此，在加入S w之后，SVM所計算的最大距離由歐式距離變更為馬氏距離。

受MCVSVM的啟發，為了解決MMCF存在的問題，也可將類內散度矩陣引入MMCF，提出了最小類內方差相關濾波器（minimum class variance correlation filter，MCVCF），其定義如下：

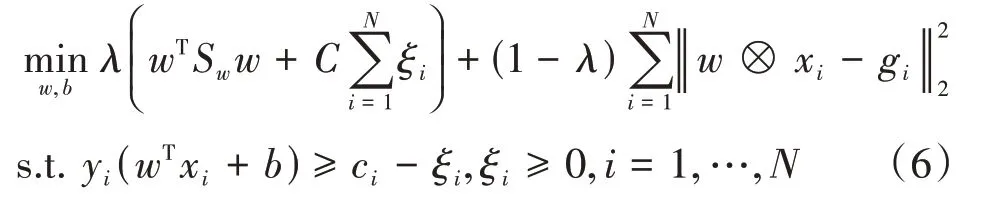
其中，MCVCF將類內散度矩陣加入到模型中，在訓練時充分利用每一類樣本的整體分布信息，能得到更加魯棒的濾波器。

但模型（6）并不能夠直接進行應用，還需要進行求解。且根據相關卷積定理［12］，相關濾波器的相關運算需通過傅里葉變換轉換到頻域中變換為相乘運算，能極大提高運算速度。因此，需先將模型（6）轉換到頻域中，再利用wolf對偶問題進行求解。

將模型轉換到頻域，由于MCVCF由兩部分構成，所以轉換過程可以分為兩個部分。首先對模型中的支持向量部分進行傅里葉變換，內積在變換過程中只是按1d的比例進行了縮放，d是樣本數據的維度則該部分變換之后如下：

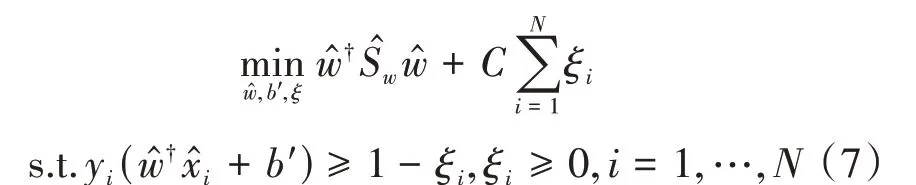
其 中，?是 頻 域 中 的w，b'=b×d，?=是頻域中A類的均值，?是頻域中的x，?表示共軛轉置。

相關濾波部分的轉換如下：

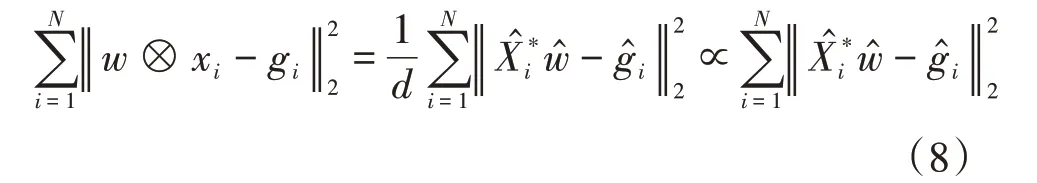
其中，是對角線元素為所有元素的對角矩陣，分別是x i、g i經過傅里葉變換轉換到頻域的數據。另外忽略掉1d，因為它是一個常數，對最終效果沒有影響。?可改寫為：

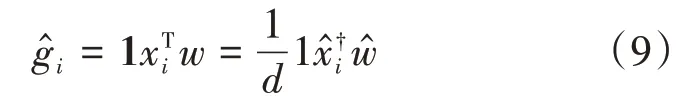
其中，1=[ 1…1]T，將式（9）代入式（8）：

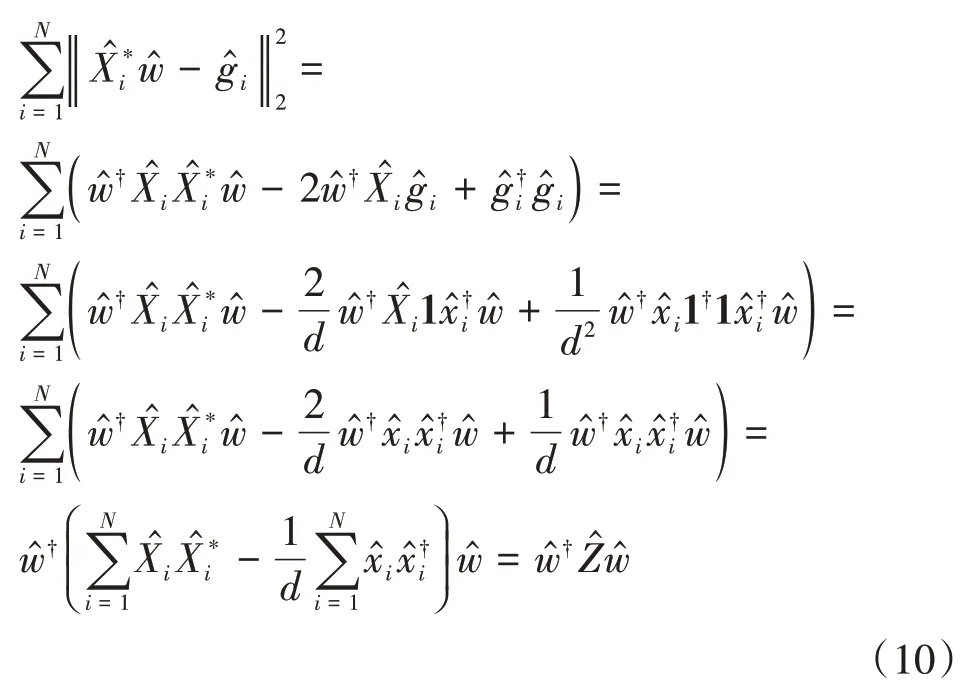
完成對兩個部分的傅里葉變換，合并成MCVCF的頻域形式：

可通過Lagrange對偶問題對式（11）進行求解，首先構造式（11）的Lagrange函數：

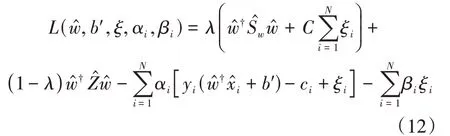
其中，αi、βi是Lagrange乘子，再對式（12）求偏導：

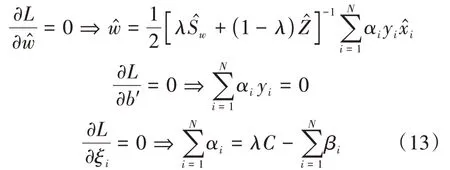
將式（13）的結果代入式（12），可得MCVCF的對偶問題：

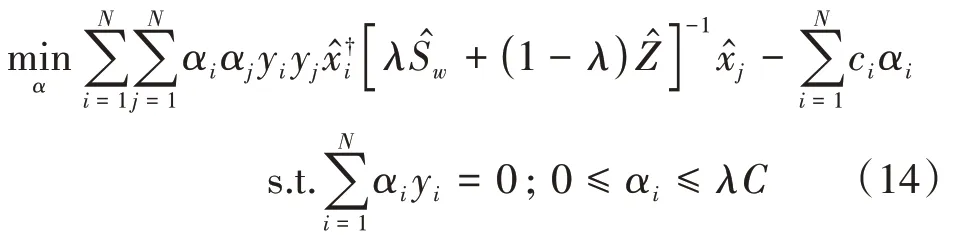
其中，α=[α1,…,αN]T。得到式（14）后，使用SMO算法進行求解，通過該算法求得Lagrange乘子向量α*，則可利用下式求解MCVCF在頻域中的濾波器向量?：

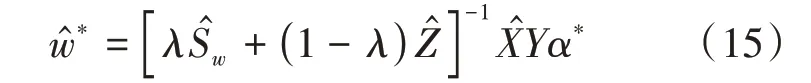
其中，Y是對角線元素為y i的對角矩陣。?是頻域中的濾波器向量，在實際應用中，還需要將其通過傅里葉逆變換轉換到空間域，并根據樣本數據大小轉換為相同尺寸的濾波模板矩陣W*，便可利用W*與待測試圖像進行互相關運算以求出相關性。

2.2 基于最小類局部保持方差的相關濾波器

在結合SVM的同時，MMCF同樣未考慮到樣本內部的結構信息。針對SVM這一事實，文獻［13］利用局部保持投影［14］的思想，提出了最小類局部保持方差支持向量機（minimum class locality preserving variance support vector machine，MCLPVSVM）。設有一數據集為U={x i|i=1,…,N}?Rd×N，則MCLPVSVM的 定 義如下：

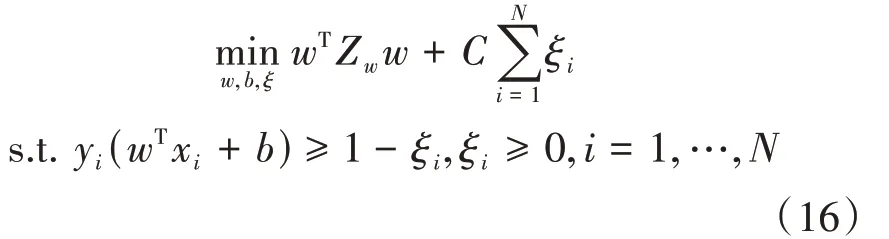
其中，Z w是局部保持散度矩陣，用于描述數據內部的結構信息。設有K=1,2兩類樣本數據，則Z w的定義如下：

其中，Z K是第K類數據的局部保持散度矩陣，其具體構造如下：

其中，X K是第K類數據的矩陣形式，D K是一個對角矩陣，其元素的定義是是W K矩陣的元素，W K是鄰接圖權重矩陣，設x Ki、x K j是第K類樣本的數據點，G是數據集U的鄰接圖，G用于表示數據局部流型結構，L=D-W是G的拉普拉斯矩陣。G共有N個節點（即數據點），如果節點i在節點j的k個最近鄰居中，則x Ki∈N K(x Kj)，以高斯核的形式構造權重矩陣W K，其元素的構造形式如下：

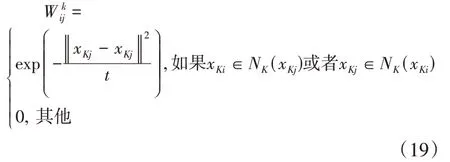
其中，t是高斯核函數參數。

MCLPVSVM較好地解決了SVM未考慮樣本內部結構的問題，因此，可將局部保持散度矩陣引入MMCF，提出最小類局部保持方差相關濾波器（minimum class locality preserving variance correla?tion filter，MCLPVCF），其定義如下：

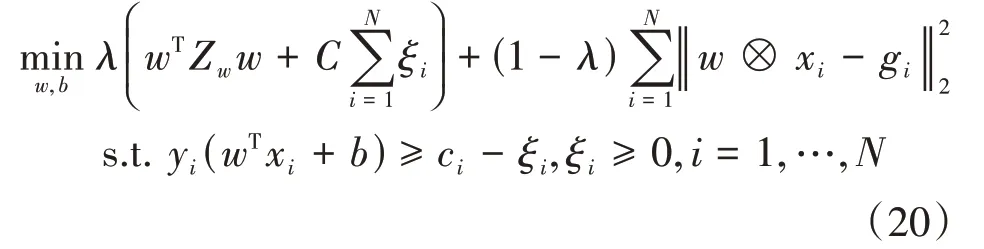
其中，Z w是局部保留散度矩陣，其定義與式（17）、（18）、（19）相同。

MCLPVCF的求解與MCVCF的求解過程基本一致，最終求解出的MCLPVCF的頻域濾波器向量是：

在實際應用中，仍需要將轉換到空間域中，得到空間域濾波器W*。

3 實驗及結果分析

為了驗證所提算法的有效性和參數對模型的影響，本節將進行仿真實驗，并在相同實驗條件下與MOSSE、OTSDF、MMCF、最大間隔矢量相關 濾 波 器［15］（maximum margin vector correlation fil?ter，MMVCF）、零混疊大間隔相關濾波器［16］（zero-aliasing maximum margin correlation filter，ZAMMCF）進行對比。所有實驗都是基于Intel i5處理器、16 GB內存、MATLAB R2020a的應用環境。

3.1 參數影響

為了討論參數對所提算法的影響，首先將進行手寫數字識別的實驗。本實驗采用的是MINIST標準手寫體數字數據集，這個數據集包含70000張手寫體數字。為了便于參數討論，從中隨機挑選1000張圖像進行實驗，其中800張作訓練集，200張作測試集。

MCVCF的參數主要有λ和C，表1給出了在不同的參數設置下MCVCF的識別率。從表1數據可以看出，λ和C的設置對識別率有一定的影響，總體來看，在λ=0.5和C=0.1左右識別率相對較高，在λ=0.7和C=1時識別率最高。

表1 不同參數下MCVCF的識別率（%）

MCLPVCF有k、λ、t和C四個參數，參數討論相較復雜，C對實驗結果的影響與MCVCF類似，因此本文只討論k、λ、t對MCLPVCF的影響。圖1給出了參數k、λ、t不同組合下的手寫數字識別的識別率。其中（a）是固定參數C=1、λ=0.6時的識別率，（b）是固定參數t=1、C=1時的識別率，（c）是固定參數k=30、C=1時的識別率。可以看出，三個參數對MCLPVCF的實驗結果有一定的影響，三個參數的共同點在于在數值偏小時識別率都較低，在增大到一定程度時識別率會趨于平穩。

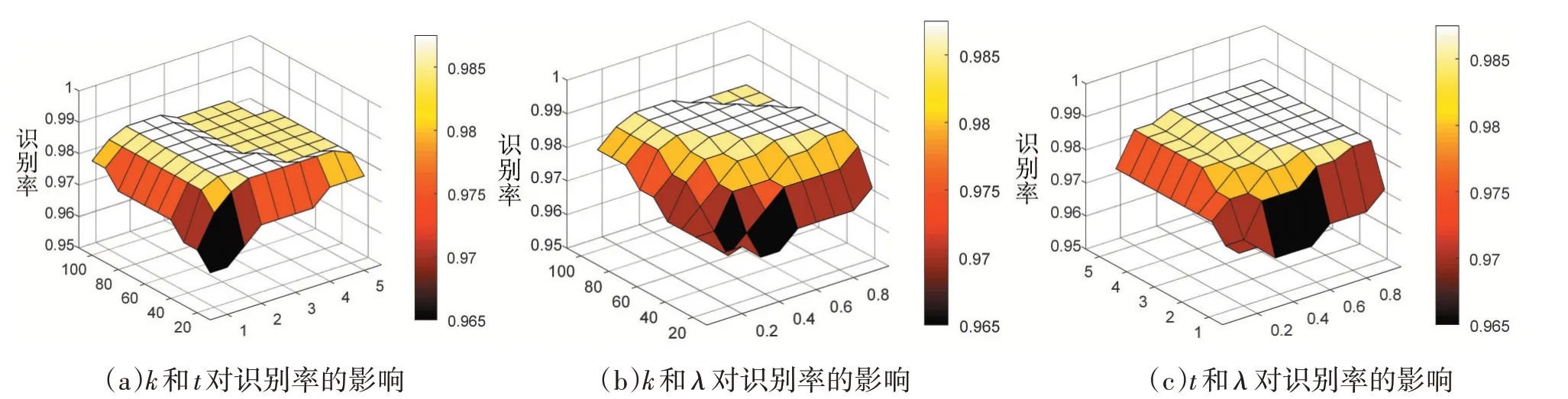
圖1 參數k、λ、t對MCLPVCF識別率的影響

3.2 檢測實驗

為了進一步驗證所提算法的有效性，本部分將進行人眼檢測實驗，并與其他相關濾波器算法作對比。此實驗采用的是Yale人臉數據集，此數據集包含15類的165張人臉圖像。從中選擇一部分人工標注剪切人眼作訓練集，再從另一部分隨機選擇15張圖像作測試集。本實驗MCVCF固定參數λ=0.6、C=1，MCLPVCF固定參數λ=0.6、C=1、k=5、t=1.5，MMCF、MMVCF和ZAMMCF固定參數λ=0.6、C=1，OTSDF固定參數λ=0.6。本實驗的評價指標是檢測準確率，所有算法所檢測出的人眼標注框與真實人眼標注框重合率大于0.3時認為檢測到了人眼，以檢測到的目標數與總體圖像數的比值作為檢測準確率。

如圖2是MCVCF和MCLPVCF的實驗效果圖，其中黑色虛線框為MCVCF標注的人眼位置，紅色實線框為MCLPVCF標注的人眼位置。

圖2 MCVCF、MCLPVCF人眼檢測效果

表2給出了所提算法與其他相關濾波器算法的實驗結果。能夠看出，MCVCF和MCLPVCF的檢測準確率相較所比較的大部分相關濾波器算法有所提升。

表2 不同濾波器的檢測準確率（%）

3.3 識別實驗

相關濾波器的另一個重要應用領域就是目標識別，因此本部分將進行一個物體識別和一個人臉識別實驗。具體實驗方法為：采用一對多的策略，選擇其中一類圖像為正類，其他類為負類，經過多次實驗求得平均識別率和標準差。

物體識別實驗采用的是COIL100物體數據集，這個數據集包含100類的7000張彩色圖像，所有圖像中的物體都進行了校準處理，并呈現出不同的角度。為了實驗的方便，將數據集中所有的圖像縮小為60×60大小，隨機選擇每類的［20，25，30，35，40，45］張圖像作訓練集，其他圖像作測試集，重復測試40次求得平均識別率。本實驗中，MCVCF固定參數λ=0.6、C=1，MCLPVCF固定參數λ=0.6、C=1、t=0.5，在訓練集圖像數目為20、30、35時k=3，其 余 情 況k=2，MMCF、MMVCF和ZAMMCF固定參數λ=0.6、C=1，OTSDF固定參數λ=0.6。

COIL100的實驗結果如表3所示，所提兩種算法的平均識別率相比其他算法都要更高，尤其相比MMCF，MCVCF能提高0.9%～1.4%，而MCLPVCF則能提高1.5%～5.6%。

表3 不同濾波器在COIL100數據集上的平均識別率及標準差（%）

人臉識別實驗采用的是AR人臉數據集，這個數據集包含120個人的3120張圖像。隨機選擇每類的［5，10，15，17，20］張圖像作訓練集，其他圖像作測試集，充分測試40次求得平均識別率。MCVCF固定參數λ=0.6、C=1，MCLPVCF固定參數λ=0.6、C=1，訓練集圖像個數為5時固定參數k=2，t=0.5，為10、15、17時k=3，t=1.5，為20時k=4，t=1，MMCF、MMVCF和ZAMMCF固定參數λ=0.6、C=1，OTSDF固定參數λ=0.6。

AR數據集的實驗結果如表4所示，可以看出，大部分情況下，所提兩種算法都取得了最優和次優的平均識別率，在訓練集圖像數目增多的情況下，這種優勢則更加明顯。

表4 不同濾波器在AR數據集上的平均識別率及標準差（%）

從上述所有實驗可以看出，無論是目標檢測還是目標識別實驗，MCVCF和MCLPVCF所取得的實驗結果都比其他濾波器尤其是MMCF要更優秀，這說明在增加了對樣本總體結構和內部結構信息的利用后，濾波器的構建和訓練得到了優化，具體應用效果得到了提升。

4 結語

本文提出了兩種基于數據分布信息的相關濾波器算法，所提算法可用于解決傳統相關濾波器尤其是MMCF樣本訓練不充分的問題。本文在詳細推導了算法模型和求解過程之后，進行了參數影響實驗、人眼檢測實驗、物體和人臉識別實驗，從實驗結果可以看出，所提算法的檢測準確率和平均識別率均取得了最優，證明了所提兩種算法增加樣本結構信息進行訓練的有效性。