受垂直激勵和水平約束的單擺系統亞諧共振分岔與混沌*

趙武 張鴻斌? 孫超凡 黃丹 范俊鍇

1) (河南理工大學機械與動力工程學院，焦作 454003)

2) (河南理工大學材料科學與工程學院，焦作 454003)

為解決一類典型工程擺的工作性能參數優選，抽象該類系統為“受垂直激勵和水平約束”的物理單擺模型.運用多尺度法解析系統的亞諧共振響應，明確了系統參數對幅值共振帶寬、多值性的作用規律.利用Melnikov 函數法，求解得到系統的同宿軌和Smale 意義上混沌的閾值條件.通過數值法解析系統單參分岔、最大Lyapunov 指數、雙參分岔及吸引域流形轉遷等動力特性，揭示了這類擺系統的亞諧共振分岔、周期吸引子倍增、周期與混沌吸引子共存等全局特性的運動規律，進一步明確了相關參數改變對系統運動形態轉化、能量分布與演變規律的作用機理，得到了相關參數對工程系統工作性能的影響和作用機制.研究結果對工程中該類典型物理系統的工作性能參數調整，及其對實際工況中系統的減振抑振提供了理論依據.

1 引言

不同于簡單的單擺，受垂直激勵和水平約束的單擺系統，是工程彈簧擺的典型物理抽象.單擺具有運動的等時性，起重機吊重系統[1，2]以及人體行走系統可簡化為單擺模型[3]，并且單擺原理應用于減振裝置也具有良好的效果[4，5].伽利略[6]和惠更斯[7]都是單擺研究的奠定者.單擺模型基礎上延伸出的彈簧擺、復擺、倒立擺等系統的物理特性，本質上往往不能簡單等同于單擺，所以得到學者們的廣泛研究[8-10]，對復雜擺系統的響應解析、穩定性、分岔和混沌的研究，也就成為擺類系統的研究重點[11-13].

蕭寒等[14]和張麗娟等[15]研究了一類外激勵作用下的彈簧擺系統的分岔和周期穩定性，明確了系統的擬周期環面破裂和陣發性進入混沌的路徑.Bek 等[16]解析出阻尼彈簧擺的二階近似非線性響應;Butikov 等[17]研究了一類具有黏性阻尼和干摩擦阻尼作用的彈簧擺，獲得了系統干摩擦阻尼確定的極限環及對稱的非黏性強迫振蕩的穩態周期性.Zhou 等[18]和Franco 等[19]研究倒立擺的亞諧分岔、混沌運動及平衡控制，獲得異宿軌臨界條件和系統參數的魯棒性.Najdecka 等[20]研究了參數激勵的雙擺動力特性，明確了同步與旋轉穩定性間的關系.

對實際應用中特定工程擺懸掛點的激勵響應的研究，也引發了學者的關注[21，22].Kholostova[23]研究了懸掛點受水平激勵的單擺，解析出系統周期運動中穩定性和不穩定周期運動的邊界條件;Jallouli 等[24]研究了諧波激勵和參數激勵作用的非線性擺的零吸引子孤子解轉換為周期穩定解的條件;Brzeski 等[25]研究了強迫Dufffing 振蕩擺的動力分岔、旋轉周期解及參數空間中的共存吸引子條件.

實際工程中的船用起吊機[26]、繩系航天器[27]及水下極端環境球形機器人重擺[28]，以及軋制工藝系統中工作輥偏心于支撐輥的軋制狀態，都可通過力學分析轉化為受垂直激勵和水平約束的單擺[29].可見，受垂直激勵和水平約束的擺系統是單擺物理模型的進一步延伸，工程應用廣泛.對此類問題的研究文獻較少，使用現有單擺物理系統的研究結論，無法明確對這類多參量作用下的工程彈簧擺的物理屬性及工作性能的優選評估.因此深入研究這類擺系統的基本物理問題和動力學機制是提升這類工程擺廣泛優化應用的關鍵.

本文較系統地研究了“受垂直激勵和水平約束的單擺系統”的基本物理問題.通過理論解析和數值計算，深入研究了該類典型工程擺系統的亞諧共振、幅頻特性、混沌、單參和雙參分岔及吸引域流形轉遷等特性，揭示了這類擺系統的工作參數變化誘發能量改變對系統動特性和工作性能的影響.

2 受垂直激勵和水平約束的單擺系統動力學方程

圖1 為受垂直激勵和水平約束的單擺模型.其中，x和y分別表示水平方向和垂直方向，o為懸掛點，擺球懸掛點受到垂直激勵y1(t)，擺球等效質量為m，不計懸掛點處質量，重力加速度為g，擺球與垂直方向夾角為u(t)，擺長為l.擺球在運動過程中受到水平方向的約束作用，表現為彈性回復力和阻尼力形式，其剛度系數和阻尼系數分別為k和c.

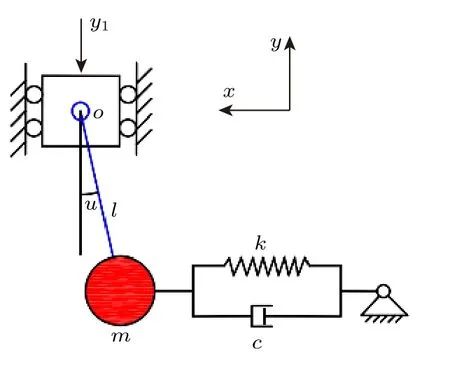
圖1 受垂直激勵和水平約束的單擺模型Fig.1.Simple pendulum model with vertical excitation and horizontal constraint.

擺球的水平位移xp和垂直位移yp可以表示為:xplsinu，ypy1－lcosu.擺球的水平速度和垂直速度可寫為:lu˙ cosu，+lu˙ sinu.取擺球懸掛點位置為重力零勢能位置，單擺系統動能為T，勢能為V，耗散能為D，圖1 所示的受垂直激勵和水平約束的單擺系統Lagrange 方程為

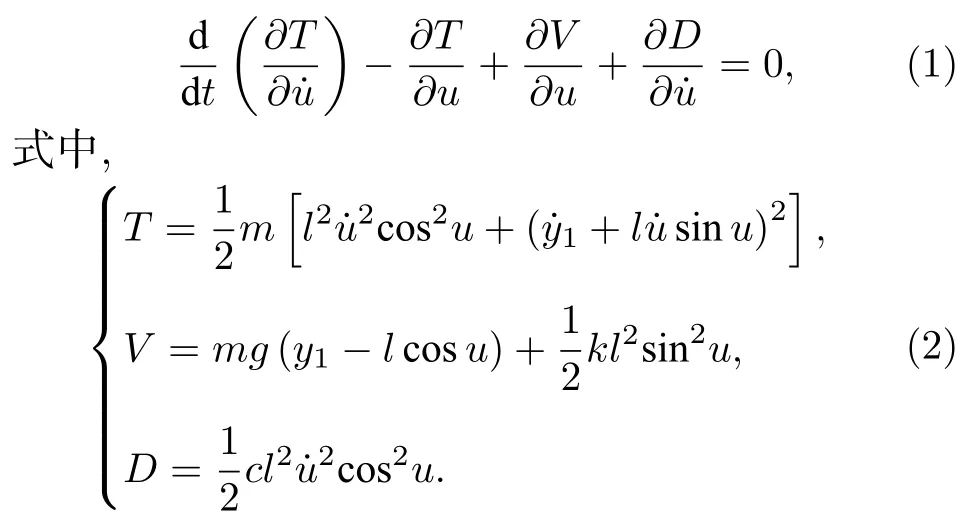
將(2)式代入(1)式，整理化簡，考慮擺角u較小時令 sinucosu ≈u，cos 2u ≈1，整理得到受垂直激勵和水平約束的單擺運動方程為

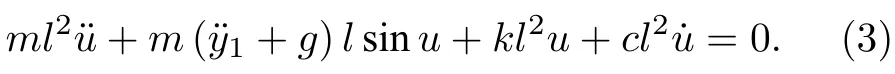
把水平剛度系數k進一步表達為非線性形式:

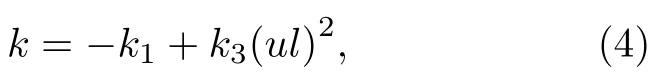
式中，k1，k3分別是一次方剛度和三次方剛度系數.

y方向垂直位移激勵型式為簡諧激勵，可表示為

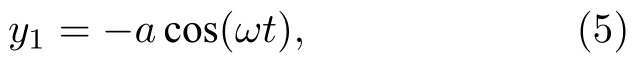
式中a，ω分別為垂直位移激勵幅值和激勵頻率.

把(4)式和(5)式代入(3)式，并進行無量綱化處理，令ω1=(k1/m)1/2，τ=ω1t，ωb=ω/ω1，u=x，整理得到

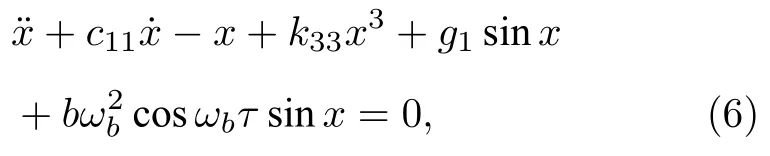
式中，c11c/(mω1)，k33ba/l，g1其中，c11為無量綱化后的阻尼系數，k33為無量綱化后的三次方剛度系數，b為無量綱化后的垂直位移激勵幅值，ωb為無量綱化后的垂直位移激勵頻率，即頻率比.(6)式是受垂直激勵和水平約束單擺的非線性系統動力學方程，是進一步分析其亞諧共振分岔和混沌行為的基礎.

3 受垂直激勵和水平約束的單擺系統的亞諧共振

受垂直激勵和水平約束的單擺系統，是工程彈簧擺的典型物理抽象.單擺懸掛點處垂直方向的位移激勵作為激勵源，會關聯水平約束擺的水平振動輸出，很多可以抽象成受垂直激勵和水平約束單擺的工程問題[30，31]，更多關注于系統中非線性共振，尤其是實際的亞諧共振導致多個響應諧波迭加引發的系統響應跳躍增減甚至混沌對實際系統工作性能的影響.

3.1 受垂直激勵和水平約束單擺系統的1/2 次亞諧共振響應

采用多尺度法[32]對系統求解.考慮到振動位移x為小量，令sinx≈x，引入小參數ε，(6)式可化為

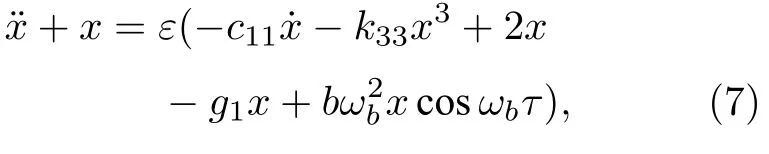
(7)式的一次近似解可記為

設置時間尺度為

時間微分為

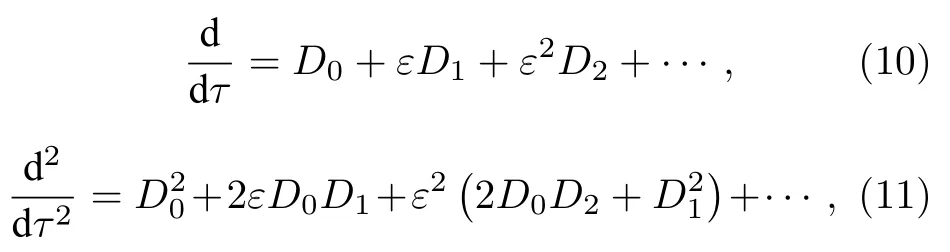
式中，Dn?/?Tn，n0， 1， 2，···.

將(8)—(11)式代入(7)式，比較ε同冪次系數，得到

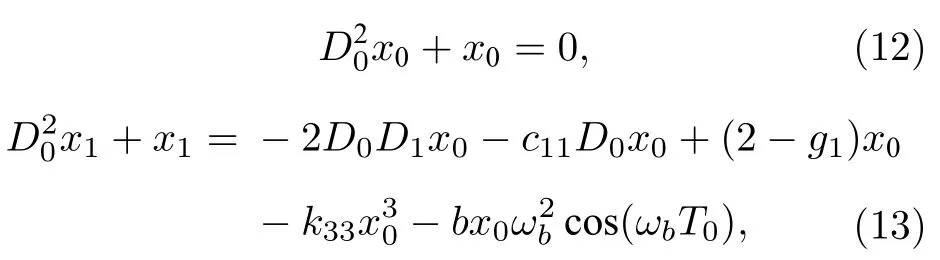
根據(12)式可得

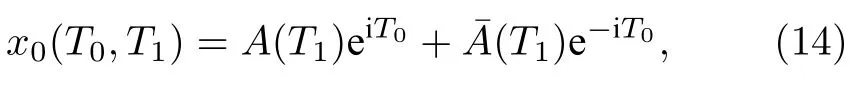
將(14)式代入(13)式得

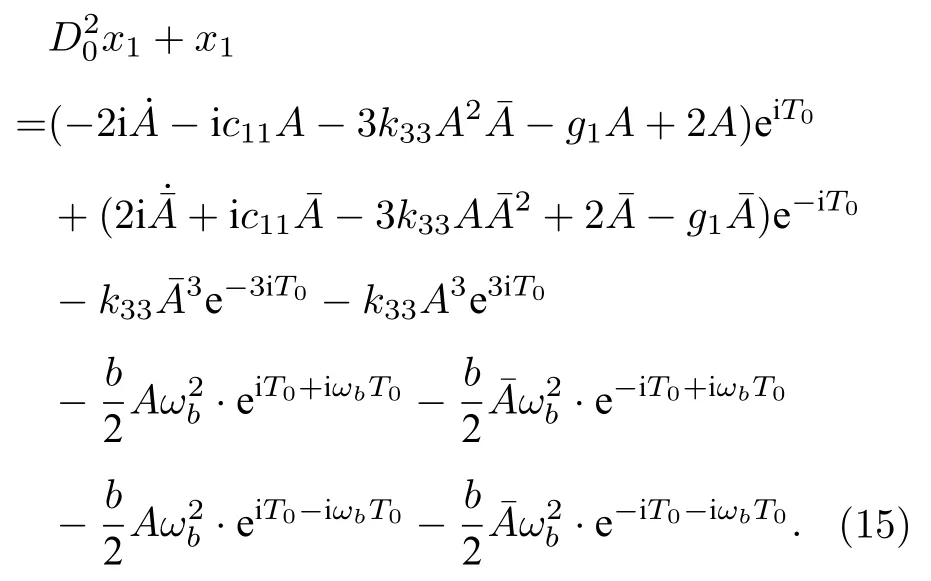
觀察(15)式，發現ωb≈ 2 時，系統會發生1/2 次亞諧共振.令:

式中，σ為調諧參數，與頻率有關.

將(16)式代入(15)式，消去久期項得

代入(17)式可得

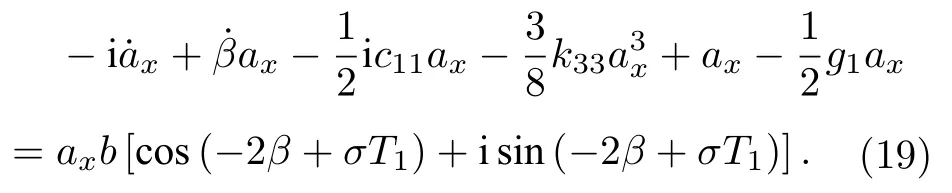
分開實部和虛部，令

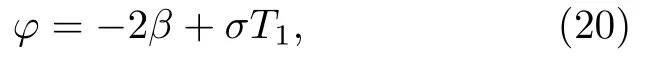
于是得到

在系統穩態工作時，令

可得

于是近似解為

將(24)式和(25)式左右兩邊平方相加，可得

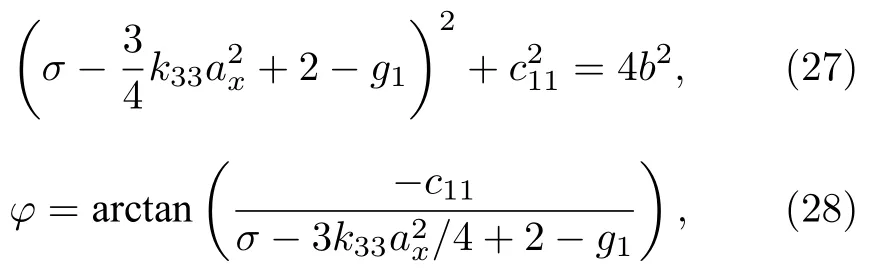
(27)式即為幅頻特性方程，(28)式為相頻特性方程.

通過數值解析，得到幅頻響應曲線.圖2 反映了b(激勵幅值a和擺長l)變化時，系統隨調諧值σ變化的幅頻響應.調諧值σ相同時，b增大，系統共振區帶寬增加;沿縱坐標方向共振曲線，左側幅值ax與b呈正相關，右側幅值ax與b呈負相關;沿橫坐標方向共振曲線，左側b與調諧值σ呈負相關，右側呈正相關.圖3 反映了k33取不同值時，系統隨調諧值σ變化的幅頻響應.調諧值σ相同時，隨k33增大，系統共振區帶寬減小;沿縱坐標方向，左右兩側的共振曲線幅值ax與k33呈負相關;沿橫坐標方向，在相同振幅值ax前提下，k33與調諧值σ呈正相關.圖4 反映了c11取不同值時，系統隨調諧值σ變化的幅頻響應曲線.在相同調諧值前σ提下，隨c11增大，系統共振區帶寬變窄;沿縱坐標方向共振曲線，左側ax與c11呈負相關，右側ax與c11呈正相關;沿橫坐標方向，在相同振幅值ax前提下，c11與調諧值σ在左側呈正相關，在右側呈負相關.

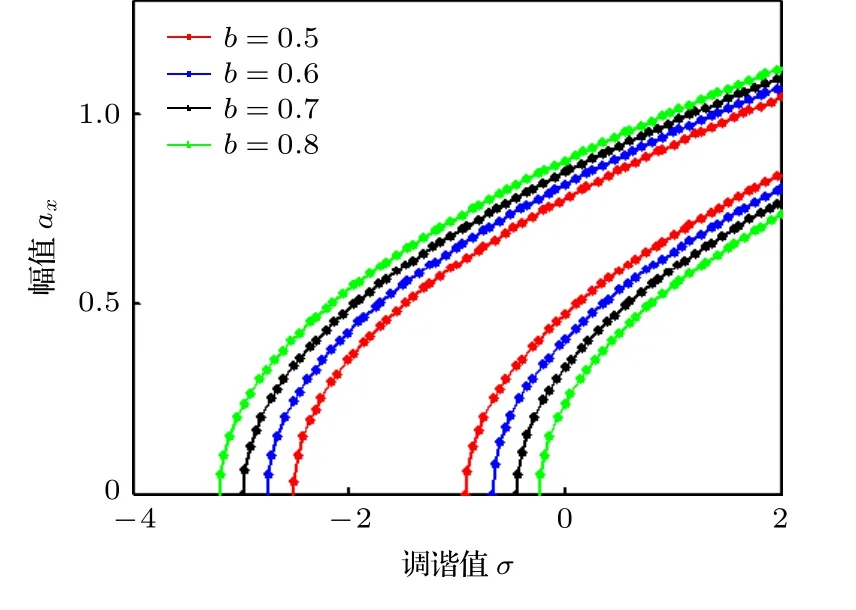
圖2 σ 變化下改變b 的幅頻響應曲線Fig.2.Amplitude-frequency response curves with different σ and b.

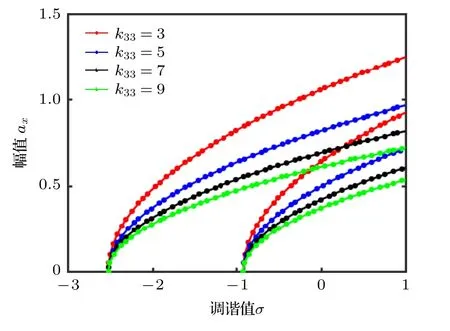
圖3 σ 變化下改變k33 的幅頻響應曲線Fig.3.Amplitude-frequency response curves with different σ and k33..

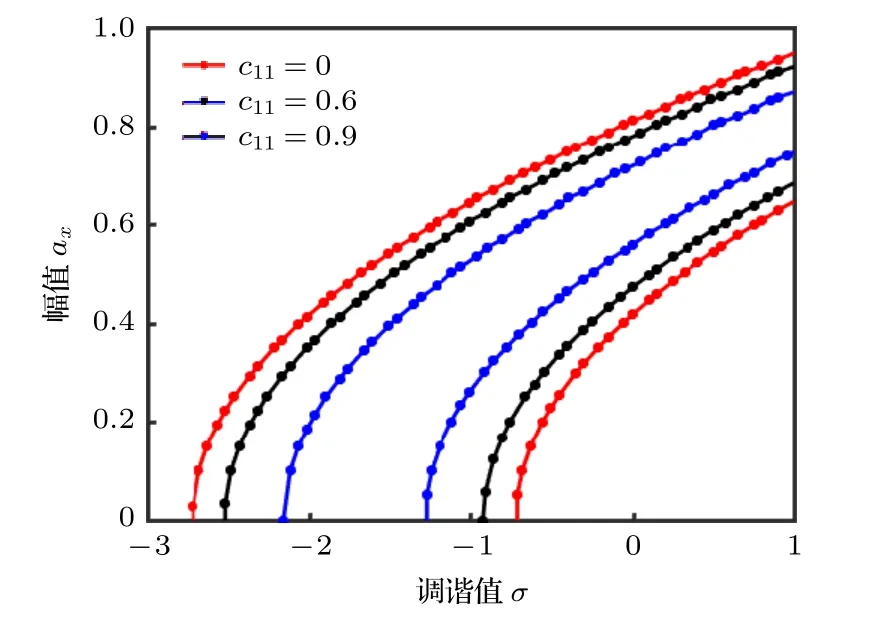
圖4 σ 變化下改變c11 的幅頻響應曲線Fig.4.Amplitude-frequency response curves with different σ and c11.

圖5 反映了調諧值σ變化時，系統隨c11變化的幅頻響應曲線.相同調諧值σ時，曲線關于c11=0對稱，隨調諧值σ絕對值增大，系統振動共振幅值減小;沿縱坐標方向共振曲線，ax與σ呈負相關;沿橫坐標方向，在相同振幅值ax前提下，c11與調諧值σ呈正相關;隨調諧值σ絕對值增大，系統振動共振區帶寬由封閉曲線轉化為開口的縮頸曲線，系統能耗的增大使共振幅值降低;且隨σ增大，振幅死亡的開口度增寬，有利于系統參數的優化閾調控.圖6 反映了調諧值σ取不同值時，系統隨k33變化的幅頻響應曲線.隨調諧值σ絕對值增大，共振區域向k33絕對值減小的方向移動;沿縱坐標方向共振曲線，左側ax與σ呈負相關，右側ax與σ呈正相關;沿橫坐標方向，在相同振幅值ax前提下，共振曲線左側k33與調諧值σ呈正相關，右側k33與調諧值σ呈負相關.

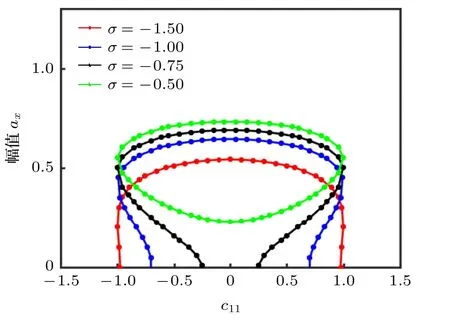
圖 5c11 變化下改變σ 的幅頻響應曲線Fig.5.Amplitude-frequency response curves with different c11 and σ.

圖6 k33 變化下改變σ 的幅頻響應曲線Fig.6.Amplitude-frequency response curves with different k33 and σ.

實際工程中受垂直位移激勵和水平約束的抽象單擺，往往在水平約束方向的小振幅輸出下，可獲得良好的工作性能.通過上述對系統的1/2 次亞諧共振幅頻特性分析，得到參數b，k33，c11以及調諧值σ對系統幅頻特性的影響規律.由b=a/l可知，增大垂直位移激勵幅值a或減小等效擺長l，將導致單擺系統共振區域帶寬增大、共振幅值增大;參數k33k3l2/，k33的大小和水平約束的三次方剛度成正比，增大三次方剛度能夠減小單擺亞諧共振振幅;參數c11c/(mw1)，c11的大小和水平約束的阻尼系數成正比，通過增大阻尼系數能夠使單擺亞諧共振區域變窄和共振幅值減小.實際工程擺中，涉及工作性能的結構參數可依據上述分析結果進行調整.

3.2 受垂直激勵和水平約束單擺系統的1/2 次亞諧共振的分岔結構

由奇異性理論定常解的局部穩定性分析，結合系統幅頻特性方程(27)得到

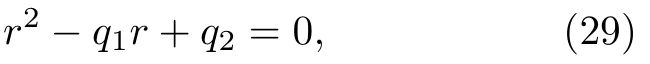
式中，

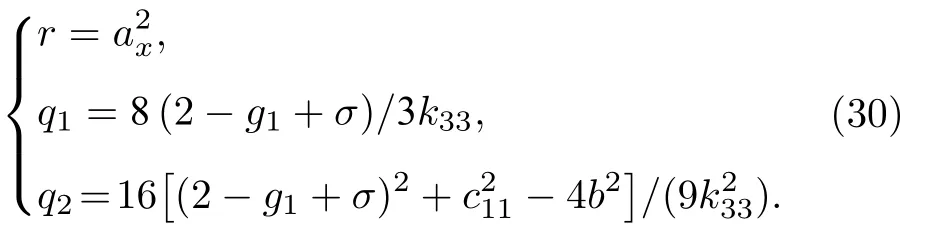
在(29)式中，令

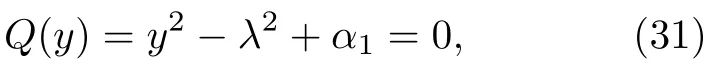
式中，y=r－q1/2，λ=q1/2，α1=q2.

a)分岔點集:

b)滯后點集:

c)雙極限點:

d)轉遷集:

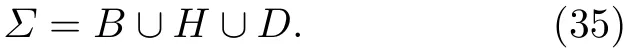
因此α1取不同值時，受垂直激勵和水平約束單擺系統1/2 次亞諧共振分岔拓撲結構如圖7 所示.當α1≥ 0 時，使α1發生變化的微小擾動都會使系統分岔結構發生變化，不利于單擺運動的穩定性;而當參數滿足α1＜ 0 時，系統分岔是持久的，利于保證單擺運動的穩定性.

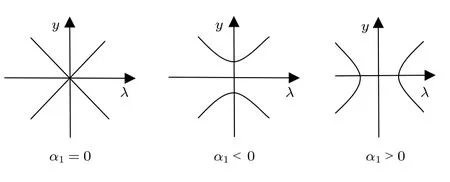
圖7 受垂直激勵和水平約束單擺系統1/2 次亞諧共振分岔拓撲結構Fig.7.Bifurcation topology of 1/2-order subharmonic resonance of a simple pendulum system with vertical excitation and horizontal constraint.

4 受垂直激勵和水平約束單擺系統的混沌分析

4.1 受垂直激勵和水平約束單擺系統的勢阱

運用Melnikov 方法，對受垂直激勵和水平約束的單擺非線性系統進行混沌運動分析與預測.令sinx ≈x，引入小參數δ，受垂直激勵和水平約束的單擺系統的運動方程(6)在δ=0 時的Hamilton系統為

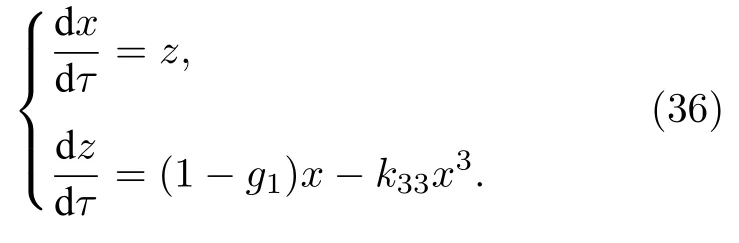
令dx/dτ=dz/dτ=0，當g1＜ 1，k33＞ 0 時，得到系統的3 個平衡點分別是

對平衡點O(0，0)，其特征值λ1和λ2是實數;對于平衡點A1和A2，其特征值λ1和λ2是共軛純虛根，所以平衡點O是不穩定的鞍點，而平衡點A1和A2是穩定的中心.令Hamilton 函數為H(x，z)，得到受垂直激勵和水平約束的單擺系統的Hamilton函數為

令其Hamilton 量為

《商標法》第十三條還規定：就相同或者類似商品申請注冊的商標是復制、摹仿或者翻譯他人未在中國注冊的馳名商標，容易導致混淆的，不予注冊并禁止使用。據此，江蘇諾法律師事務所律師樊國民認為相似商標在一定條件下存在侵權行為。他說：“行為人未經商標權人許可，在相同或類似商品上使用與其注冊商標相同或近似的商標，或者其他干涉、妨礙商標權人使用其注冊商標，損害商標權人合法權益的行為，即構成商標侵權。”

式中，h為常數.

由(38)式和(39)式，得到相軌線方程:

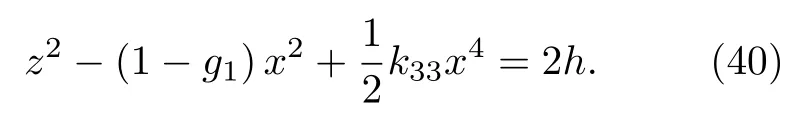
勢能函數U(x)可表示為

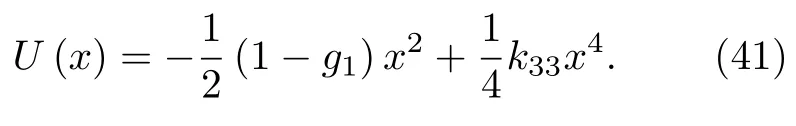
Hamilton 系統(38)的勢阱曲線和相軌線分別如圖8(a)和圖8(b)所示.圖8(a)中，對稱的雙勢阱W1和W2分別對應于穩定中心點，勢壘對應于不穩定鞍點.當把系統中的質點運動理解為孤立振子或振子群型式的運動時:一方面，對稱勢阱W1和W2之間的勢壘為系統穩定的周期運動提供了過渡平臺，當系統振子運動能量較小而不能穿越勢壘時，振子在W1或W2勢阱內做小幅值的穩定周期運動，對應于圖8(b)中的封閉橢圓相軌線，最后將穩定于中心點;另一方面，當系統振子獲得越過勢壘的足夠能量后，會在勢阱W1和W2之間大范圍運動，個別能量高的活躍振子在勢阱壁和勢壘平臺間發生碰撞、反彈、折回和沖擊，使系統運動復雜化，對應于圖8(b)中的O點或其他相軌線.系統能量變化，會引發系統運動相軌線的拓撲結構改變，系統的運動狀態隨之改變.圖8(a)中，隨擺長l增大，勢阱的開口寬度和深度都減小，說明系統的擺動運動能量更多的轉移到振動運動能量上，能量在運動形態間交換，在圖8(b)的局部放大結構圖8(c)中，擺長l增大時，系統從O點出發的相軌線會在不同擺長的運動路徑間發生躍遷和跌落的路徑轉遷，使得系統運動復雜化.這種受垂直激勵和水平約束的單擺系統，是工程彈簧擺的典型物理抽象.例如機構中的兩個彈性接觸輥在服役狀態下發生動態彈性形變，即1 個工作循環中，兩輥間的彈性形變(擺長)的動態連續變化引起的能量轉遷會使系統的運動路徑在不同的相軌線之間切換，使得系統運動復雜化.

圖8 (a)勢阱曲線;(b)，(c)相軌線及其局部放大圖Fig.8.(a) Potential well curve;(b)，(c) phase track and its enlarged view.

4.2 受垂直激勵和水平約束單擺系統的同宿軌與混沌預測

當h=0 時，可得(38)式同宿軌道為

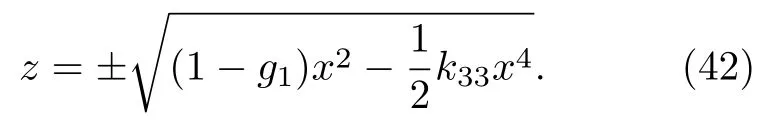
取τ=0，z=0 可解得

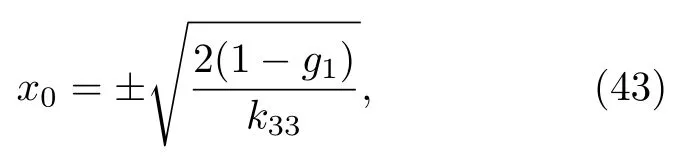
因dx/dτ=z，對(42)式積分并整理得

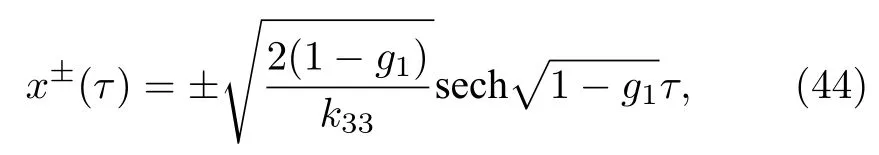
由此得系統的同宿軌道參數方程為

可把受垂直激勵和水平約束的單擺系統的Melnikov 函數表示為

利用(45)式可得

將(47)式代入系統Melnikov 函數(46)得到

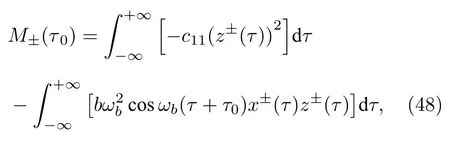
計算得到系統發生混沌運動的Melnikov 閾值為

由Melnikov 理論可知，當(49)式存在簡單零點時，系統(6)存在Smale 馬蹄意義上的混沌.因此系統在1/2 次亞諧共振情況下，當滿足

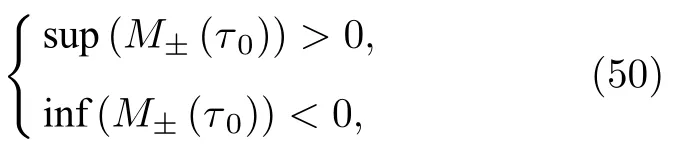
即:

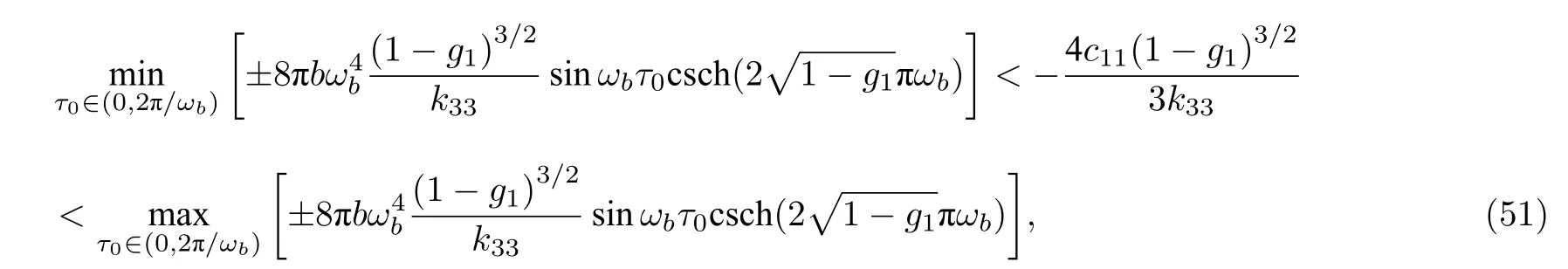
存在M±(τ0)0 且?M±(τ0)/?τ0/0，系統可發生Smale馬蹄意義的混沌.

圖9 直觀反映了系統發生混沌的臨界參量b，c11，ωb之間的制約關聯條件.曲面的上部空間參數組合引發系統混沌運動，當c11接近0.5 時，b值越大，越易引發系統混沌.根據Melnikov 函數預測條件，選取符合混沌臨界參數c11=0.5，k33=1.5，g1=0.8，b=0.6，ωb=2，計算單擺系統的混沌吸引子空間結構，如圖10 所示.圖10 中混沌吸引子呈現中心對稱分布，藍色與紅色分別代表單擺系統順時針和逆時針運動的混沌吸引子，運動過程中系統參數改變，導致系統能量的交替變化，使系統運動復雜化.圖11 對應系統擺長變化的分岔，隨擺長l增大，系統歷經二周期、單周期、二周期、四周期到混沌運動的演化過程.結合圖10 與圖11，系統在ωb=2 時的混沌吸引子是成對的兩個旋轉對稱分岔點的余維.

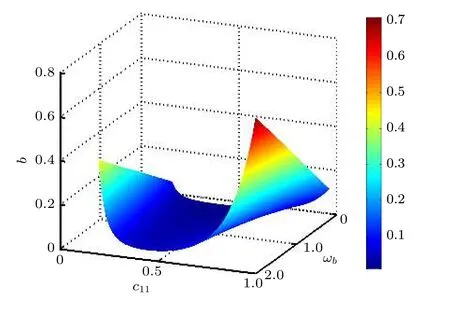
圖9 系統混沌運動的參數條件Fig.9.Parameter conditions for chaotic motion of the system.

圖10 單擺系統亞諧共振在ωb=2 時的混沌吸引子Fig.10.Chaotic attractor of simple pendulum system when ωb=2.

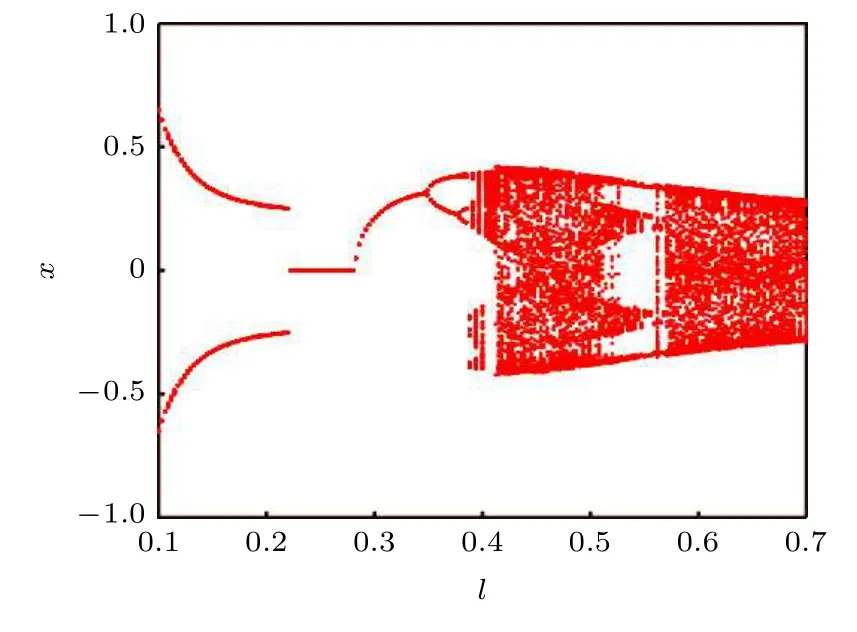
圖11 擺長l 變化下的分岔圖Fig.11.Bifurcation diagram with different l.

5 受垂直激勵和水平約束的單擺系統的亞諧共振仿真

對受垂直激勵和水平約束的單擺系統(6)進行數值仿真，如無特殊說明，參數如下:c11=0.618，k33=1.3，g1=0.28，b=0.48.通過仿真分岔、最大Lyapunov 指數和雙參耦合分岔等系統特性，研究單擺系統亞諧共振與混沌的演化機制.

5.1 受垂直激勵和水平約束單擺系統的亞諧共振分岔與混沌

5.1.1ωb對單擺系統分岔的影響

隨ωb變化的單擺系統的運動分岔及最大Lyapunov 指數如圖12(a)和圖12(b)所示.可見，隨ωb增大，單擺系統歷經“單周期-二周期-四周期-混沌-四周期-混沌-二周期-混沌-四周期-二周期-單周期”的系列復雜運動變化，且中間交替發生多次的倍周期分岔.

圖12 ωb 變化下的(a)分岔和(b)最大Lyapunov 指數Fig.12.(a) Bifurcation and (b) maximum Lyapunov exponent with different ωb.

ωb變化的相圖和時間歷程如圖13(a)—(f)所示.ωb=0.5，1.02，1.8 時，系統分別處于單周期、二周期、混沌運動狀態;且ωb=1.8 的時間歷程圖(圖14(a)—(c))顯示出系統運動中較明顯的交疊拍振共振行為，伴隨b(垂直位移激勵幅值或擺長)變化，系統能量也不斷交替改變，系統共振頻次和振幅帶寬都發生變化.比較圖13(d)—(f)發現，ωb變化改變了單擺的運動周期，其變化過程與系統動力學行為(圖13(a)—(c))相一致.

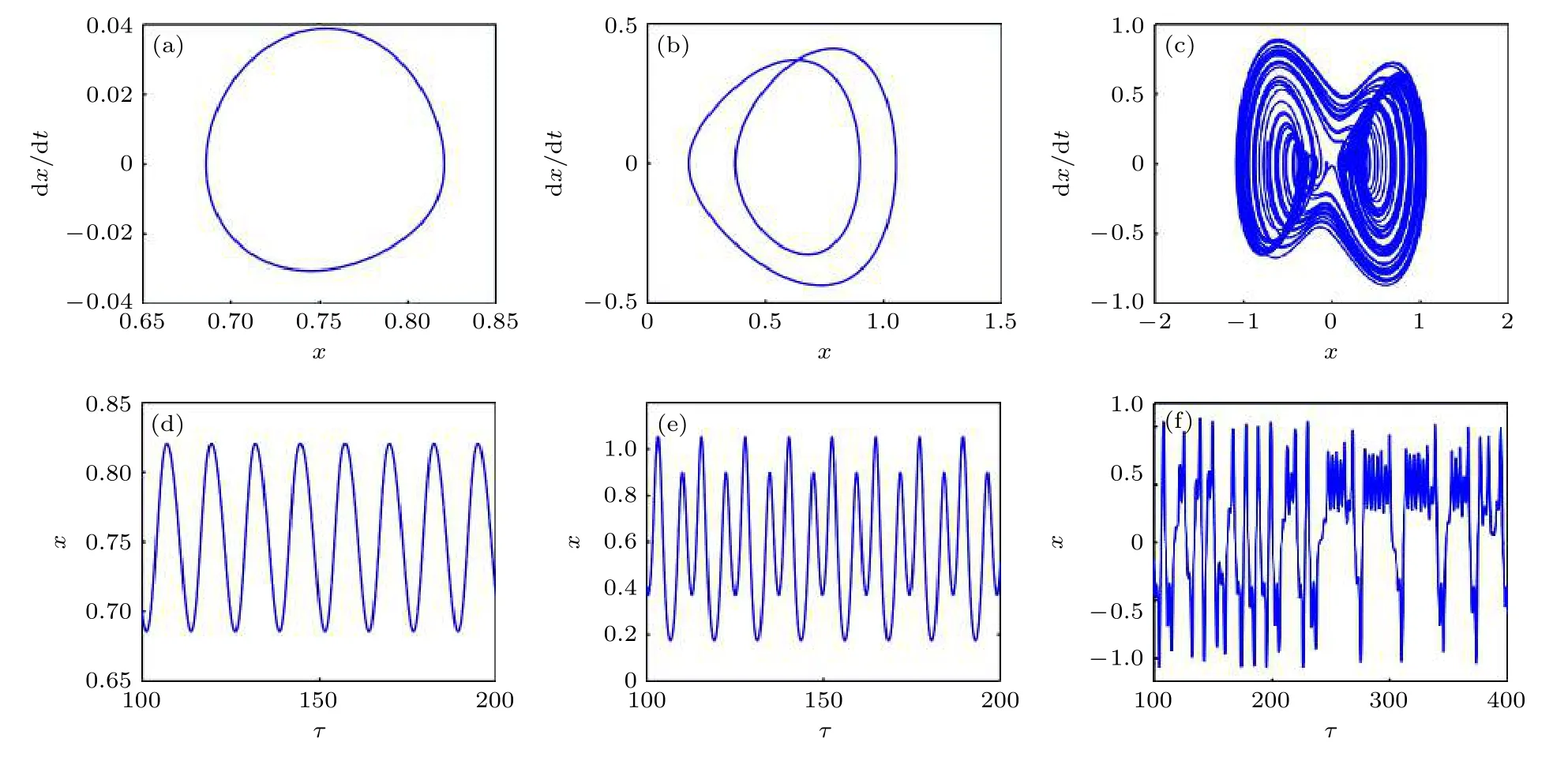
圖13 ωb 變化下的(a)-(c)相圖和(d)-(f)時間歷程圖 (a)，(d) ωb=0.5;(b)，(e) ωb=1.02;(c)，(f) ωb=1.8Fig.13.(a)-(c) Phase diagram and (d)-(f) time history diagram with different ωb :(a)，(d) ωb=0.5;(b)，(e) ωb=1.02;(c)，(f) ωb=1.8.

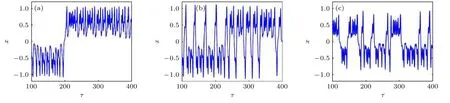
圖14 當ωb=1.8 時b 變化下的時間歷程圖 (a) b=0.28;(b) b=0.38;(c) b=0.58Fig.14.Time history diagram when b changes and ωb=1.8:(a) b=0.28;(b) b=0.38;(c) b=0.58.

5.1.2c11對單擺系統分岔的影響

隨c11變化的系統分岔和最大Lyapunov 指數如圖15(a)和圖15(b)所示.可見，隨水平約束阻尼系數c11增大，系統歷經“混沌-四周期-二周期-混沌-八周期-四周期-二周期-單周期”的系列復雜運動變化過程.

圖15 c11 變化下的(a)分岔和(b)最大Lyapunov 指數Fig.15.(a) Bifurcation and (b) maximum Lyapunov exponent with different c11.

c11變化的相圖和時間歷程如圖16(a)—(f)所示.其中圖16(a)—(f)中，c11=0.6，0.63，1.2 時，系統分別處于雙曲混沌、混沌、單周期運動狀態;c11=0.6，系統表現為左右兩中心的相軌跡被鞍點所吸引的雙曲混沌;c11=0.63，系統表現出對稱性降低，有序性增加的混沌態.隨c11繼續增大，系統由倒倍周期分岔發展為c11=1.2 的單周期運動.比較圖16(d)—(f)發現，c11變化改變了水平約束單擺系統的運動周期，其變化過程與系統動力學行為(圖16(a)—(c))相一致.

圖16 c11 變化下的(a)-(c)相圖和(d)-(f)時間歷程圖 (a)，(d) c11=0.6;(b)，(e) c11=0.63;(c)，(f) c11=1.2Fig.16.(a)-(c) Phase diagram and (d)-(f) time history diagram with different c11:(a)，(d) c11=0.6;(b)，(e) c11=0.63;(c)，(f) c11=1.2.

5.1.3g1對單擺系統分岔的影響

隨g1變化的系統分岔圖及最大Lyapunov 指數曲線如圖17(a)和圖17(b)所示.可見，隨g1增大，單擺系統歷經“混沌-四周期-二周期-單周期”的運動狀態改變.g1取不同值的相圖和時間歷程如圖18 所示.其中圖18(a)—(c)，隨系統歷經雙曲混沌、混沌、二周期等運動狀態的改變，這與圖18(d)—(f)中，g1變化引起的系統動力學行為相一致.

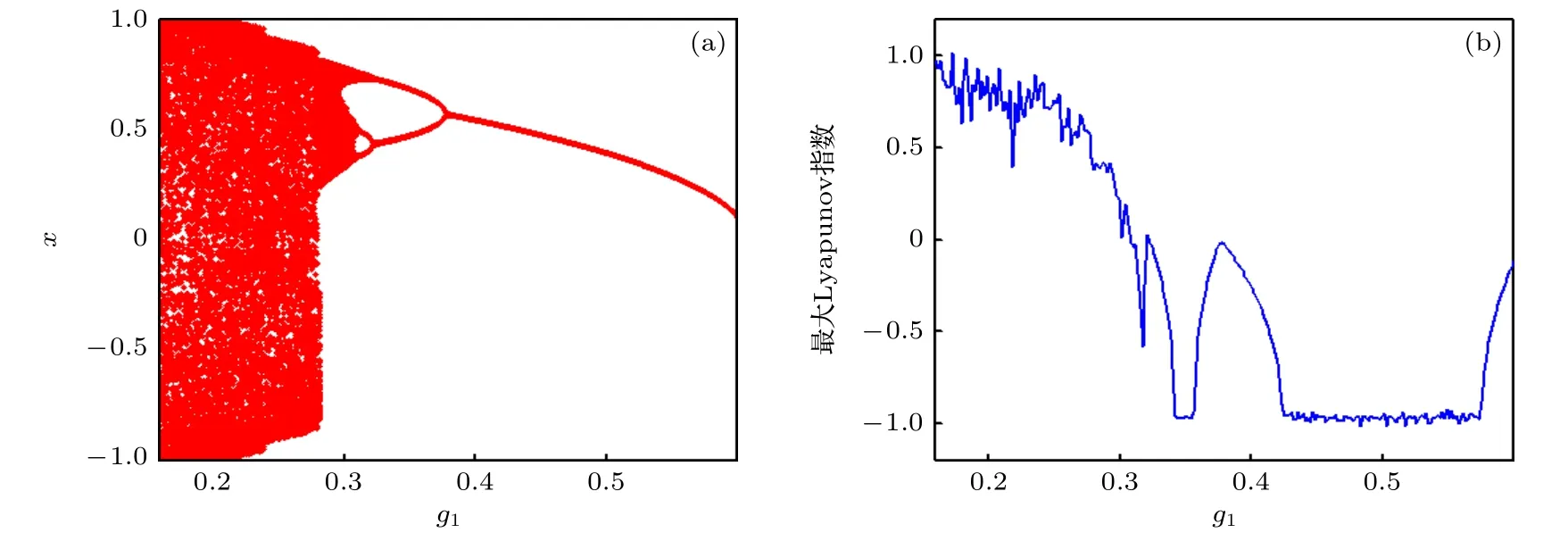
圖17 g1 變化下的(a)分岔和(b)最大Lyapunov 指數Fig.17.(a) Bifurcation and (b) maximum Lyapunov exponent with different g1.

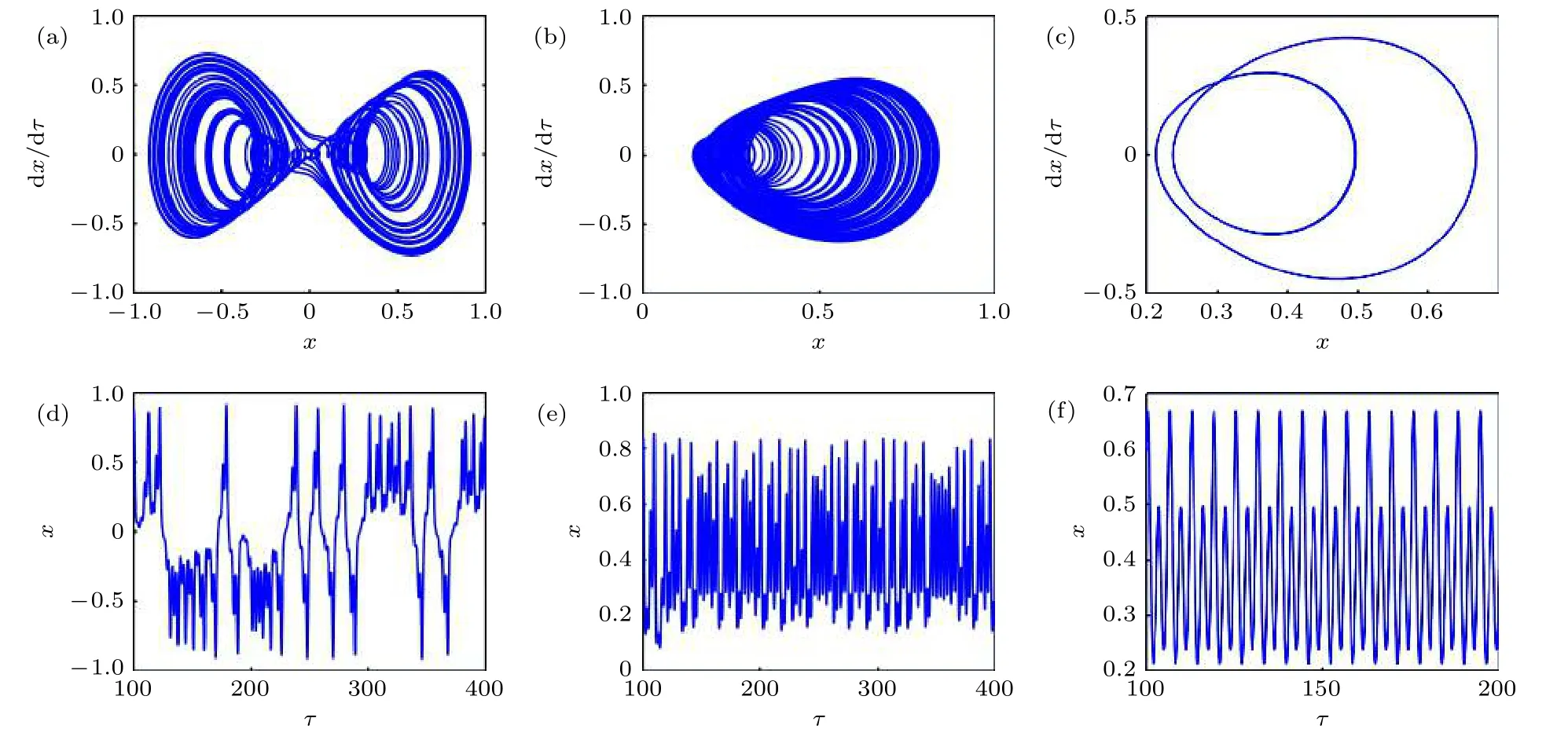
圖18 g1 變化下的(a)-(c)相圖和(d)-(f)時間歷程圖 (a)，(d) g1=0.27;(b)，(e) g1=0.28;(c)，(f) g1=0.36Fig.18.(a)-(c) Phase diagram and (d)-(f) time history diagram with different g1:(a)，(d) g1=0.27;(b)，(e) g1=0.28;(c)，(f) g1=0.36.

5.1.4k33對單擺系統分岔的影響

隨k33變化的系統分岔及最大Lyapunov 指數曲線如圖19(a)和圖19(b)所示.隨k33增大，系統歷經“單周期-二周期-四周期-八周期-混沌”系列運動狀態的改變過程.隨k33變化的相圖和時間歷程如圖20 所示.其中圖20(a)—(c)，k33=0.6，1.2，1.4 時，系統分別處于四周期、混沌、雙曲混沌運動.隨k33變化，單擺的周期性也發生改變如圖20(d)—(f)，其變化過程與系統動力學行為(圖20(a)—(c))相一致.

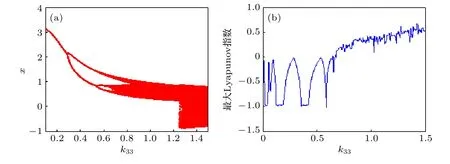
圖19 k33 變化下的(a)分岔和(b)最大Lyapunov 指數Fig.19.(a) Bifurcation and (b) maximum Lyapunov exponent with different k33..

圖20 k33 變化下的(a)-(c)相圖和(d)-(f)時間歷程圖 (a)，(d) k33=0.6;(b)，(e) k33=1.2;(c)，(f) k33=1.4Fig.20.(a)-(c) Phase diagram and (d)-(f) time history diagram with different k33:(a)，(d) k33=0.6;(b)，(e) k33=1.2;(c)，(f) k33=1.4.

5.1.5b對單擺系統分岔的影響

隨b變化單擺系統的運動分岔及最大Lyapu nov 指數如圖21(a)和圖21(b)所示.可見，隨b增加，單擺系統歷經“單周期-二周期-四周期-混沌-四周期-二周期-單周期”的系列復雜運動變化.

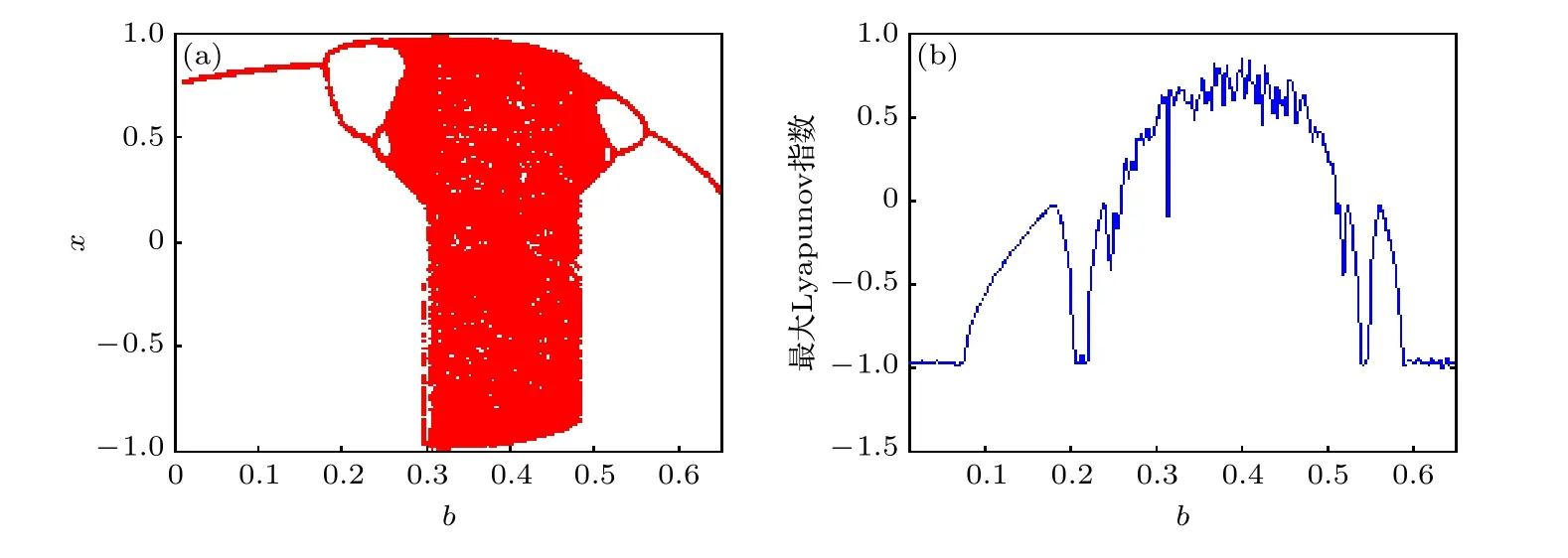
圖21 b 變化下的(a)分岔和(b)最大Lyapunov 指數Fig.21.(a) Bifurcation and (b) maximum Lyapunov exponent with different b.

b變化的相圖和時間歷程如圖22(a)—(f)所示.其中圖22(a)—(f)中，b=0.19，0.28，0.36 系統分別處于二周期、混沌、雙曲混沌的運動狀態.b=0.36 的時間歷程圖(圖23(a)—(c))顯示出系統運動中較明顯的交疊拍振共振行為，伴隨ωb變化，系統能量也不斷交替改變，系統共振頻次和振幅帶寬都發生變化.比較圖22(d)—(f)發現，b變化改變了單擺的運動周期，其變化過程與系統動力學行為(圖22(a)—(c))相一致.

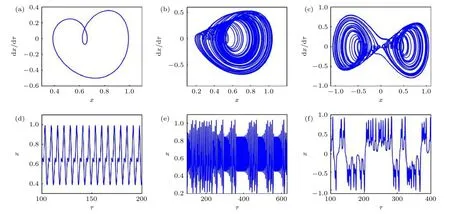
圖22 b 變化下的(a)-(c)相圖和(d)-(f)時間歷程圖 (a)，(d) b=0.19;(b)，(e) b=0.28;(c)，(f) b=0.36Fig.22.(a)-(c) Phase diagram and (d)-(f) time history diagram with different b:(a)，(d) b=0.19;(b)，(e) b=0.28;(c)，(f) b=0.36.

圖23 當b=0.36 時ωb 變化下的時間歷程圖 (a) ωb=1.3 (b) ωb=1.5;(c) ωb=1.7Fig.23.Time history diagram when ωb changes and b=0.36:(a) ωb=1.3;(b) ωb=1.5;(c) ωb=1.7.

5.2 受垂直激勵和水平約束單擺系統的亞諧共振雙參分析

通過分析方程(6)隨相關變量的雙參組合，研究受垂直激勵和水平約束的單擺系統在雙參量耦合變化下的動力行為演化，映射雙參域變化下的單擺系統分岔運動特性.

參數ωb耦合c11的系統運動特性如圖24(a)所示.在區域“Ch1”，“Ch2”和“Ch3”的組合取值，反映系統運動做混沌運動;其他區域組合取值，系統做周期運動.圖24(a)中，考慮參量的一維變化，沿“L1”路徑變化參數ωb，系統運動狀態變化過程與圖12 一致;沿著“L2”路徑變化參數c11，系統運動狀態變化過程與圖15 一致，這也在一定程度上佐證了單參數分岔對系統運動改變的結果.

參數c11耦合k33的系統運動特性如圖24(b)所示.區域“Ch3”組合取值會導致系統運動的不穩定性比區域“Ch1”，“Ch2”大;當c11，k33在“Ch1”，“Ch2”和“Ch3”區域邊緣組合取值時，會導致系統運動由混沌轉向周期運動.

參數k33耦合g1的系統運動特性如圖24(c)所示.區域“Ch1”內組合取值，最大Lyapunov 指數為正，系統做混沌運動.參數g1耦合參數b的系統運動特性如圖24(d)所示.區域“Ch1”內組合取值，系統最大Lyapunov 指數大于零，系統做混沌運動，當g1和b在其他區域內組合取值時，最大Lyapunov 指數為負，系統做周期運動.

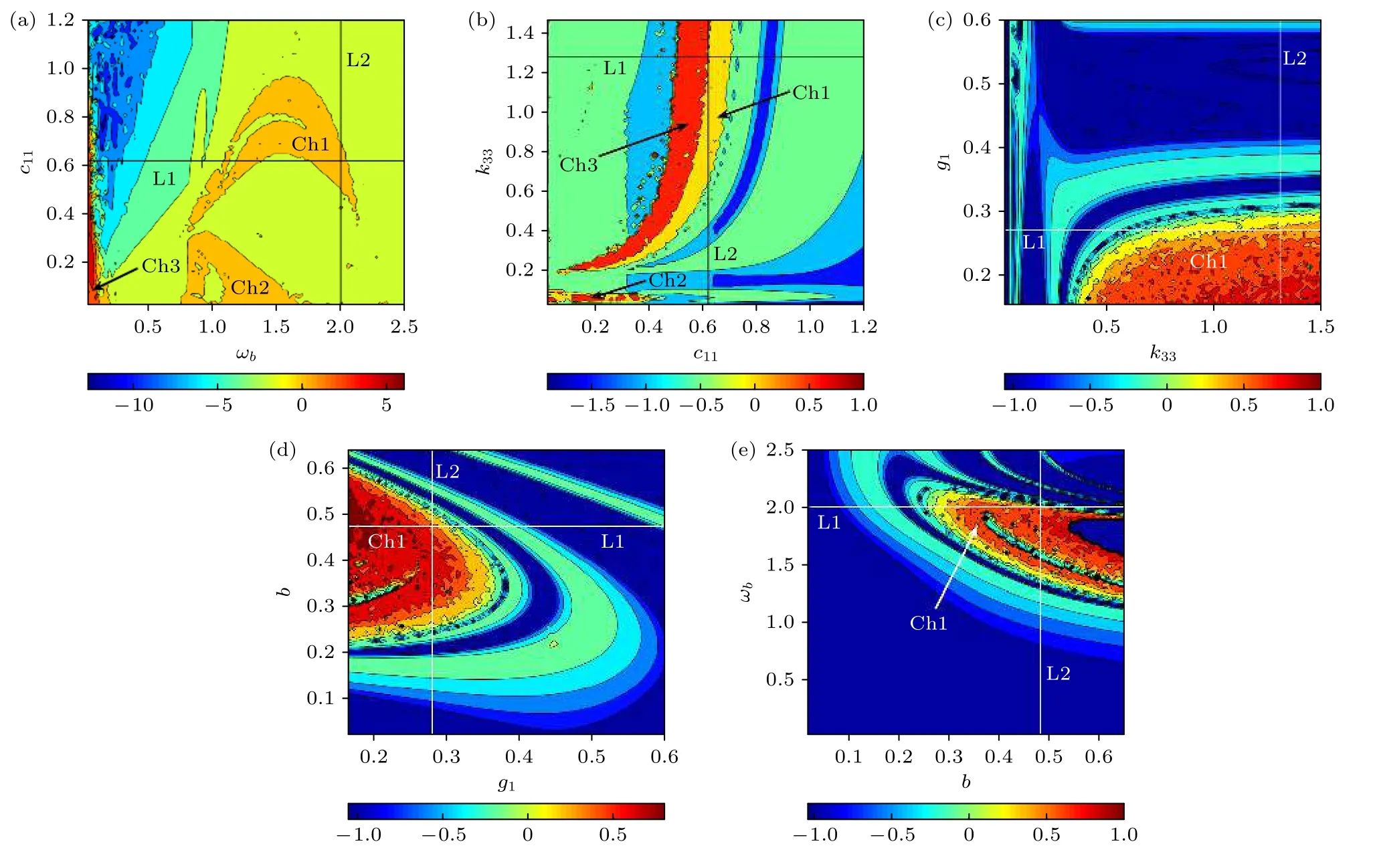
圖24 單擺非線性系統在雙參數域上的運動 (a) ωb-c11;(b) c11-k33;(c) k33-g1;(d) g1-b;(e) b-ωbFig.24.Motion of a simple pendulum nonlinear system in the bi-parameter domain:(a) ωb-c11;(b) c11-k33;(c) k33-g1;(d) g1-b;(e) b-ωb.

參數b耦合參數ωb組合的系統運動特性如圖24(e)所示.區域“Ch1”內組合取值，系統最大Lyapunov 指數為正，系統做混沌運動;當b和ωb的組合取值在“Ch1”區域邊界時，系統最大Lyapunov 指數在0 附近變動，系統發生混沌和周期運動的轉換.

上述對受垂直激勵和水平約束的單擺系統在雙參數域上的運動特性分析，明確了參數ωb，c11，k33，g1和b的組合取值對系統運動狀態的影響，系統發生周期運動與混沌運動的轉換邊界，系統最大Lyaounov 指數發生穿越0 的突變，系統動力特性也變得復雜.

6 受垂直激勵和水平約束單擺系統亞諧共振的吸引域

分析受垂直激勵和水平約束的單擺系統亞諧共振分岔與混沌等運動狀態轉換，能量變化是本質驅動內因.動力系統運動過程吸引子、吸引域的流形轉遷所表現出的能量演化機制，決定了系統的運動特性.

研究參數b改變對受垂直激勵和水平約束的單擺非線性系統的吸引子、吸引域的影響，揭示單擺系統運動過程中能量變化影響下的全局動力特性.參數b變化引發的單擺系統吸引子、吸引域的轉遷如圖25 所示.

b=0.11 的吸引域如圖25(a)所示.此時系統存在兩個周期吸引子，且每個吸引子所在的吸引域(藍色和綠色)邊界清晰，二者相互纏繞，系統處于穩定運動狀態;如圖25(b)所示，隨b增大至b=0.23 時，周期吸引子倍增，存在4 個周期吸引子，每兩個周期吸引子所在吸引域(藍色和綠色)邊界清晰，吸引域帶寬變窄，還有進一步稀疏的演化趨勢，這些都在一定程度上反映出b的改變會誘發單擺系統內部穩定域的變化.

b=0.32 的吸引域如圖25(c)所示.系統歷經倍周期分岔運動的極限位置到達邊界，系統的運動狀態發生激變，出現混沌吸引子，系統能量的改變導致單擺的運動失穩.如圖25(d)所示的b=0.35，系統內部繼續激變，混沌吸引子所在的吸引域區域減少，出現周期吸引子，并且兩個周期吸引子及其所在的吸引域中心對稱分布，反映出垂直激勵引發的能量改變激發出單擺系統的周期吸引子與混沌吸引子共存，系統所表現出的運動形式則取決于初始狀態.

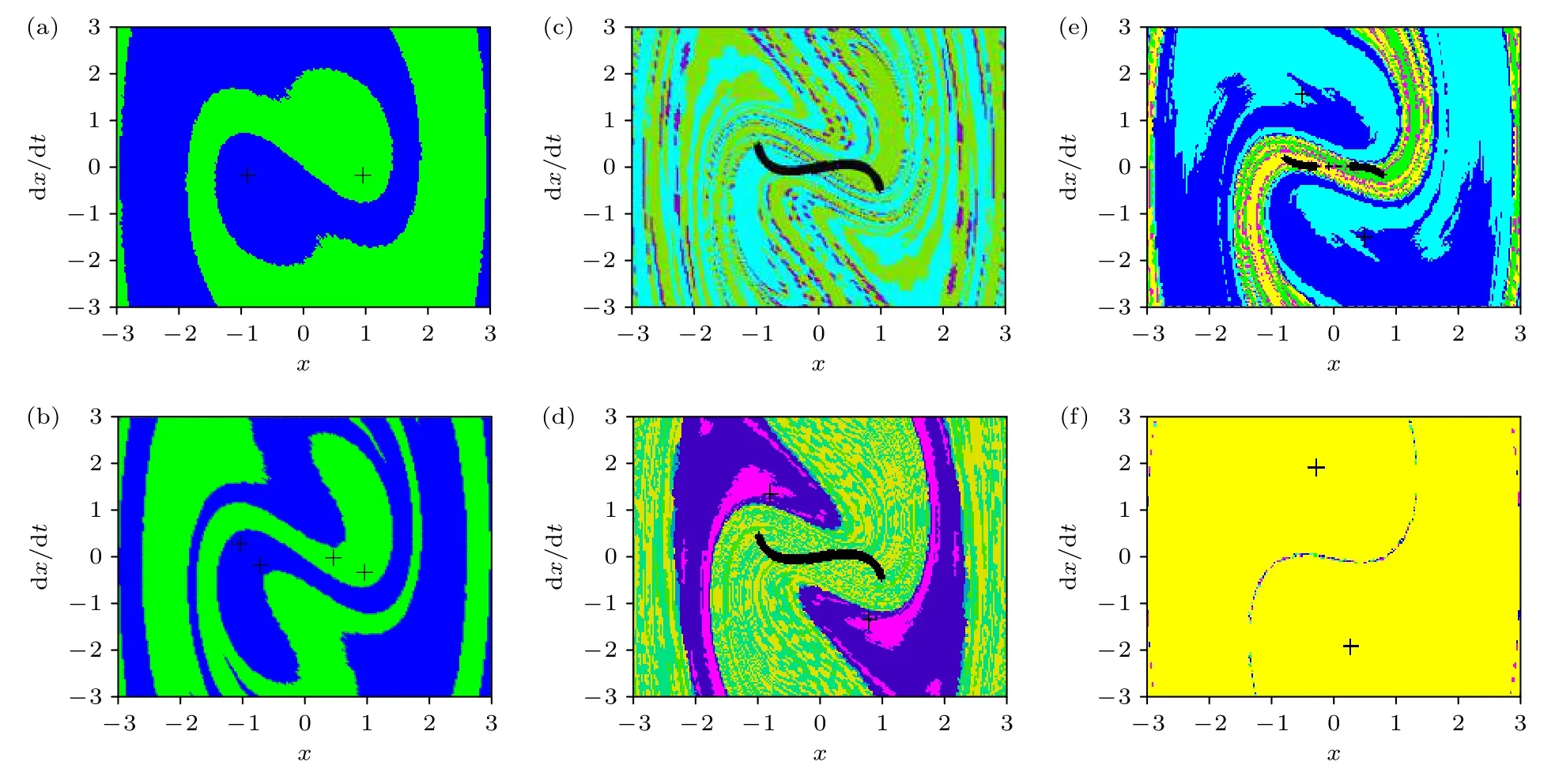
圖25 系統在參數b 變化時的吸引子、吸引域 (a) b=0.11;(b) b=0.23;(c) b=0.32;(d) b=0.35;(e) b=0.49;(f) b=0.81Fig.25.Attractor and attraction domain of the system when the parameter b changes:(a) b=0.11;(b) b=0.23;(c) b=0.32;(d) b=0.35;(e) b=0.49;(f) b=0.81.

b=0.49 的吸引域如圖25(e)所示.混沌吸引子分散，所在的吸引域變窄，密集程度降低，并且周期吸引子和混沌吸引子共存，兩個周期吸引子所在的吸引域面積增大，該條件下垂直激勵引發的能量變化激發出單擺系統的周期吸引子聚集，系統所表現出的運動形式依然與初始狀態密切相關.b=0.81 的吸引域如圖25(f)所示，系統存在兩個周期吸引子，且兩個周期吸引子所在的吸引域相互環繞，呈中心對稱分布，系統處于周期運動狀態，反映出垂直激勵所引起的能量變化引起單擺系統周期吸引子能量增大，系統主要表現為周期運動.

可見，參數b變化改變了系統中的能量分布，導致系統周期吸引子倍增，混沌吸引子出現，系統經歷倍周期分岔通向混沌;當系統在周期吸引子和混沌吸引子共存條件下，各自吸引域邊界會因系統能量變化，不斷發生邊界的侵蝕、融合的復雜過程.在混沌吸引子消失后，周期吸引子及其吸引域中心對稱分布，這都在一定程度上反映出單擺系統能量影響下的全局動力特性.

7 結論

受垂直激勵和水平約束的單擺系統，是工程彈簧擺的典型物理抽象.本文系統地研究了這類工程擺的物理特性，研究結果對實際工程應用中涉及工作性能的參數調整，奠定了理論依據.通過對該系統的亞諧共振分岔和混沌分析，結論如下:

1)增大水平約束阻尼系數和三次方剛度系數，有利于減小單擺系統共振幅值;增大水平約束阻尼系數可減小單擺系統共振區域帶寬;增大垂直位移激勵幅值將增大系統共振幅值、增加共振區域帶寬.

2)對該系統的單參分岔研究表明，垂直位移激勵幅值、激勵頻率、水平約束阻尼系數和三次方剛度系數等參數變化，都將導致系統運動特性的改變，這與傳統單擺中的阻尼對運動過程無影響結論不同.上述參量變化，本質上改變了系統中的能量分布，使得單擺系統發生倍周期分岔、倒倍周期分岔、周期運動和混沌運動等動力學行為.

3)對系統在不同參量條件下的相軌跡和時間歷程的分析，表明方程(6)中的g1相當于關聯了系統擺長和運動周期的耦合項，無論擺長還是運動周期使得系統能量降低，系統都會通過參數g1的耦合，使得能量發生轉換，維持系統振動.

4)對該系統的雙參數域分岔研究表明，通過合適選擇系統參數，可有效控制該系統的振動行為，并且通過參數的匹配優選能有效避免混沌的發生.進一步通過對系統吸引子、吸引域的分析，揭示了系統能量變化對運動形態的演化機理.

上述結論為受垂直激勵和水平約束的單擺模型的工程應用提供重要理論依據，同時對實際工況下的減振抑振提供了理論參考.