最優輸運無網格方法及其在液滴表面張力效應模擬中的應用
周浩 李毅 劉海 陳鴻 任磊生
(中國空氣動力研究與發展中心,超高速碰撞研究中心,綿陽 621000)
基于網格的數值方法(如有限元、有限體積、有限差分等)在大變形、不連續等問題中遇到挑戰,因此人們提出了多種無網格方法.最優輸運無網格方法是一種新型拉格朗日無網格方法,但是繼承了有限元方法在邊界表征、邊界處理等方面的優勢,在表面張力模擬中具有較大潛力.基于拉格朗日方程,通過將表面張力勢能加入拉格朗日函數,得到的表面張力廣義力精確地作用在流體表面,而且表面張力系數是唯一的輸入參數.給出了最優輸運無網格方法軸對稱離散格式.通過對二維/三維泊肅葉流、靜止和振動的液滴、液滴變形等典型問題的仿真分析,驗證了最優輸運無網格方法在表面張力問題模擬中的精度和收斂性.
1 引言
精確可靠的模擬表面張力對液滴變形與運動的影響在環境工程、微納米工程以及醫藥工程等領域有著十分重要的應用.采用基于網格的數值方法模擬此類問題往往需要復雜的界面追蹤算法,典型的如流體體積函數法[1,2]和水平集方法[3]等.因此,越來越多的研究者采用拉格朗日粒子類方法模擬表面張力相關現象,利用粒子本身實現對邊界的自動追蹤,極大地簡化了算法,其中最常用的數值方法是光滑粒子動力學(smoothed particle hydrodynamics,SPH)[4,5]方法.在SPH 方法中,主要有兩種方法來考慮表面張力的影響:粒子間相互作用力(inter-particle interaction force,IIF)方法[6-10]和連續力方法(continuum surface force,CSF)[11].IIF 方法來源于如下思想,即表面張力來自于液體表面分子之間和內部分子之間作用力的差異.受此啟發,在SPH 方法中,可以通過在宏觀粒子之間加入額外遠程吸引力和近程排斥力來近似模擬表面張力.這種方法簡單靈活,粒子之間的額外作用力形式非常多.這種方法的缺點是表面張力系數不是輸入參數,而是需要先模擬某個標準算例,然后測量與這種宏觀粒子之間吸引力等價的表面張力系數.此外,這種方法往往存在不收斂的問題.CSF方法通過給不同的流體賦以不同的色值(color)來區分不同的流體,利用不連續的色函數(color function)求解表面法向以及曲率來計表面張力,然后將只作用在表面的力轉換為連續的體積力.SPH方法中,界面法向向量及其曲率的計算誤差一般較大.無論哪種表面張力模擬方法,SPH 方法都存在如下固有缺點:1) SPH 形函數不能嚴格滿足1 階精度(特別是粒子分布不均勻或者自由界面處),導致收斂性不好,常常需要對形函數及其導數進行修正[12,13];2)形函數不滿足Kronecker delta 性質,因此位移邊界條件處理復雜,一般需要通過各種虛粒子處理邊界條件.因此,本文嘗試采用一種新型無網格方法模擬表面張力問題,即最優輸運無網格 (optimized transportation meshfree,OTM)方法[14].
OTM 方法采用粒子系統離散連續介質,利用局部最大熵(local maximum entropy,LME)[15-17]形函數構造連續場,并結合數學中的最優輸運理論計算系統的動能積分.相比于其他無網格方法,OTM 方法在精度、收斂性、邊界處理以及數學理論基礎上均具有優勢.OTM 方法具有無網格方法能夠處理大變形的優點,同時又繼承了有限元方法的部分優點,如形函數嚴格滿足一階精度、形函數在邊界處滿足弱Kronecker delta 性質等.當前,OTM 方法已經成功應用于金屬侵徹[18]、超高速碰撞[19-21]、裂紋擴展[22]以及熱傳導等問題[23],但是將其應用于表面張力模擬還未見文獻報道.
本文從拉格朗日方程出發,從能量的角度考慮表面張力的影響,即將表面能加入到拉格朗日函數中,得到的表面張力廣義力精確地作用在流體表面,而且表面張力系數是唯一的輸入參數.為了減少計算量,推導了軸對稱形式的OTM 離散格式,用于三維算例數值模擬,并給出了詳細的計算流程.通過模擬泊肅葉流并與解析解對比,驗證了本文基本離散格式和軸對稱處理的正確性.通過模擬靜止液滴,并與Young-Laplace 公式對比,驗證了表面張力處理的正確性.模擬了液滴的周期振蕩問題并與解析解對比,嚴格驗證了液滴中速度分布的空間收斂性.最后,模擬了液滴在重力、表面張力以及界面共同作用下的形變問題,考察了液滴中的壓力分布并與理論解對比,進一步驗證了本文OTM 離散格式.
2 OTM 方法
2.1 連續介質離散
OTM 方法中的連續介質離散介于拉格朗日有限元與SPH 方法之間.OTM 方法將有限元網格中每個小網格轉換為1 個粒子,位于小網格形心.對于三角形,形心為三條中線的交點.粒子存儲所有的物理量,與SPH 方法類似.同時,保留所有的網格節點,其中存儲了速度和位置,如圖1 所示.初始時刻,邊界上只有節點,且節點隨著流場運動.邊界節點很好地表征了連續介質的邊界位置,與拉格朗日有限元方法類似.此外,由于局部最大熵形函數滿足弱Kronecker delta 性質,邊界條件處理簡單.拋棄有限元方法中單元和節點之間的固定連接關系,而是采用近鄰粒子搜索方式動態確定,從而可以處理大變形,這與SPH 方法類似.
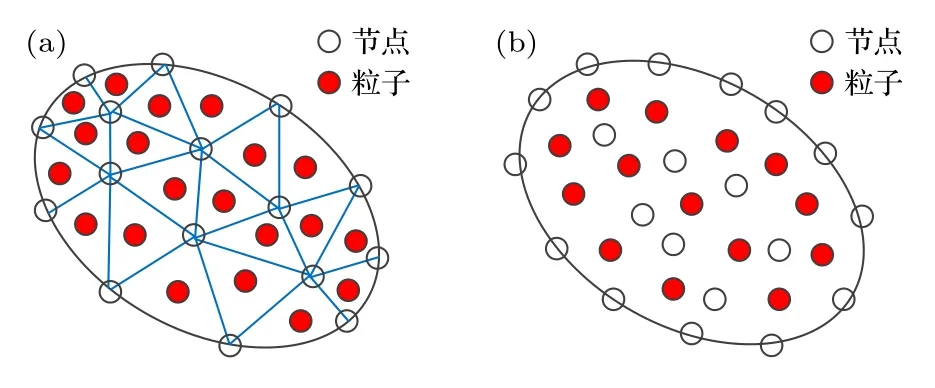
圖1 利用有限元網格將連續介質離散為粒子和節點(a)有限元網格;(b)用粒子與節點離散連續介質Fig.1.Continuum discretized by particles (red symbols)and nodes (white symbols) in the OTM method by means of finite element mesh:(a) Finite element mesh;(b) continuum discretized by particles and nodes.
2.2 LME 形函數
最優輸運無網格方法與更新拉格朗日有限元方法最大的1 個區別是采用LME 形函數,因此不需要網格,屬于無網格方法.給定1 個節點集xa(a1,2,···,n),每個節點的形函數記為Na(x) .利用形函數可以從離散數值插值出1 個連續場:
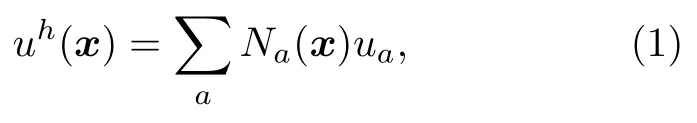
其中,uh(x)是插值出來的連續場,ua是物理量u在節點a處的值.在有限元和SPH 等方法中,形函數及其導數都具有簡單解析表達式,但是LME形函數沒有顯式的解析表達式,而是需要數值求解.
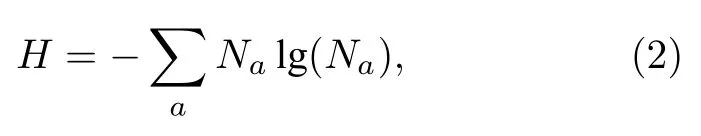
其中,由于x是固定值所以將其省略.為了減少計算量,形函數一般都是局域的,即當 |x-xa| 大于某一臨界值時,形函數Na(x) 為零.因此,可以定義如下形函數影響域平均大小:
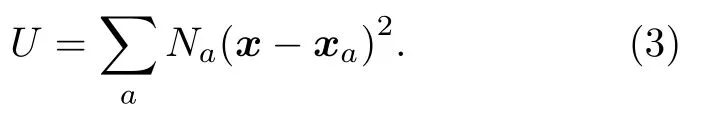
形函數影響域越大,計算量越大.LME 形函數的基本思路是讓形函數熵最大,同時影響域又盡量小,因此,構造了如下優化問題:

其中,β是1 個可調參數,用于調節兩個目標的權重.最后1 個約束條件表示形函數嚴格滿足一階精度.上述優化問題解的存在性、唯一性以及求解方法文獻[15-17]中有詳細論述,本文只給出最后結果.LME 形函數可以寫成如下形式:
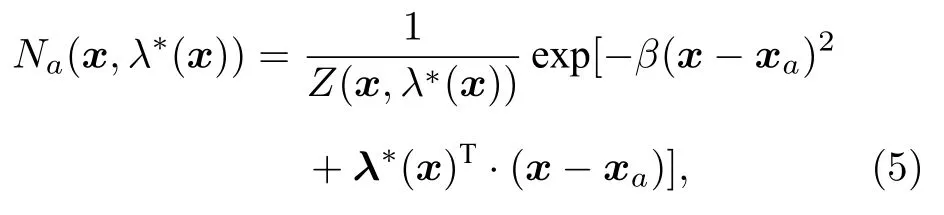
其中Z函數的定義為

λ*(x)是以下無約束優化問題的解:
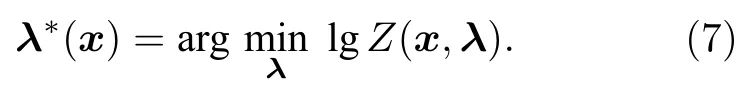
定義:
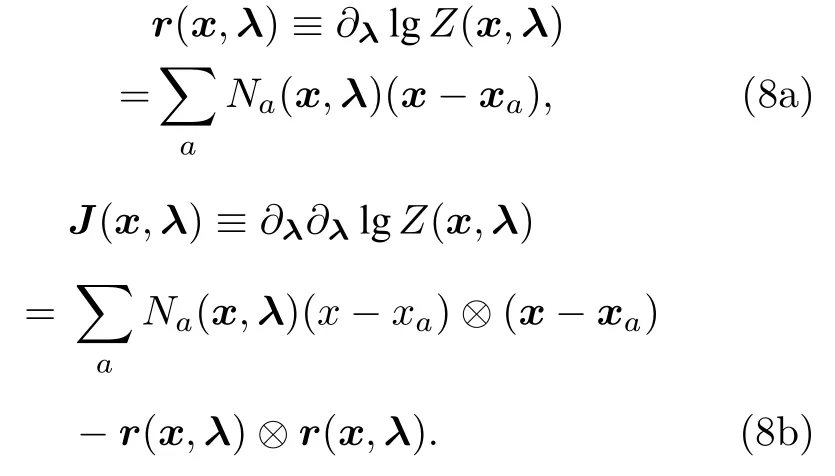
那么,可以采用如下迭代方法求解λ*(x) :
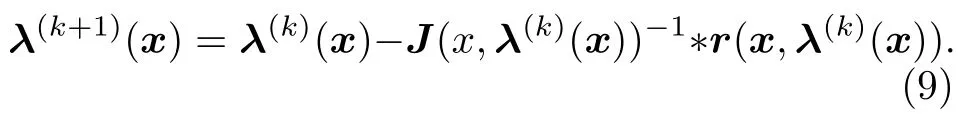
初始時刻,λ(0)一般取零.流場發生變化后,λ(0)一般取上1 個時刻的λ*.當β等于零時,得到的最大熵形函數是全局的,不適合數值計算.當β趨于無限大時,即不考慮熵最大,只要求形函數影響域最小,那么LME 形函數可以連續過渡到有限元線性形函數.LME 形函數具有以下特點:1)滿足一階精度;2)不依賴網格;3)邊界處滿足弱Kronecker delta 性質;4)形函數非負.
得到λ*(x) 與形函數后,形函數導數為
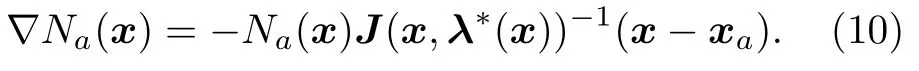
2.3 基本離散方程
首先考慮無黏、可壓縮以及等溫流體.當初始狀態已知,節點的位置描述了流場的形變的流動,實際上完全描述了流場,因此,節點的位置可以當成系統的廣義坐標.本文下標p表示粒子,用下標a,b,c表示節點.由于無黏,這是1 個保守系統,拉格朗日方程為

其中,E是系統動能,V 是系統勢能,fa是廣義節點力,va是節點速度,xa是節點位置,N是節點總數.系統動能和勢能為所有粒子動能和內能之和:
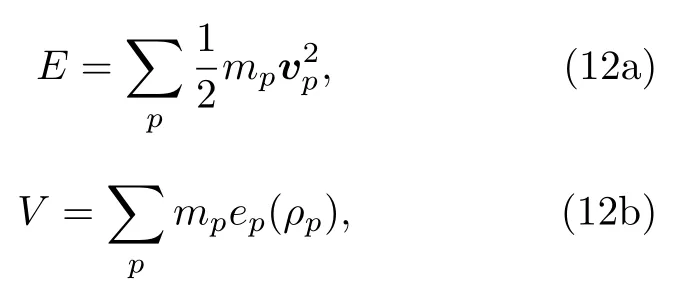
其中mp表示粒子質量,vp表示粒子速度,ep表示粒子單位質量內能,ρp表示粒子密度.
粒子內能和壓力的關系通過物態方程(equation of state,EOS)描述:
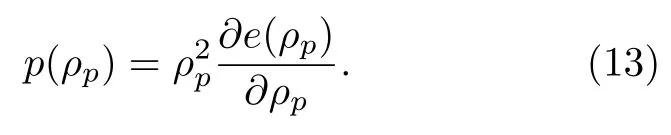
與有限元一樣,粒子位置和速度可以通過節點位置和速度插值得到:
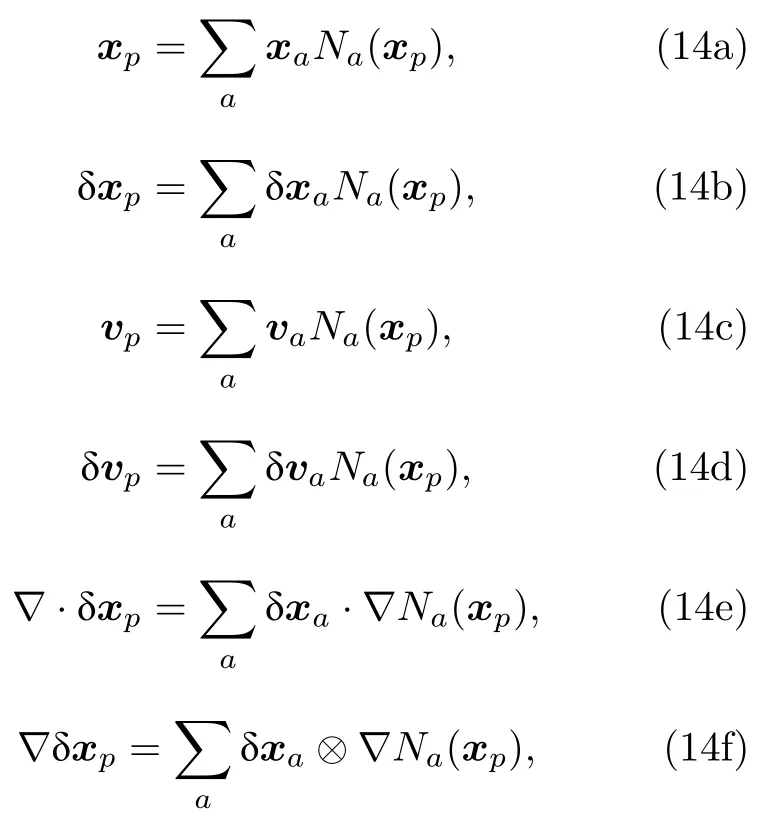
其中 δxp和 δxa分別為粒子和節點的虛位移,Na(xp)表示節點a處形函數在粒子p處的值,?Na(xp) 表示形函數梯度,求和是對粒子的所有近鄰節點.粒子密度變化和位置變化的關系由連續性條件給出:

將(14e)式代入(15)式,得到

利用求導鏈式規則,并且利用(13)式和(16)式,得到
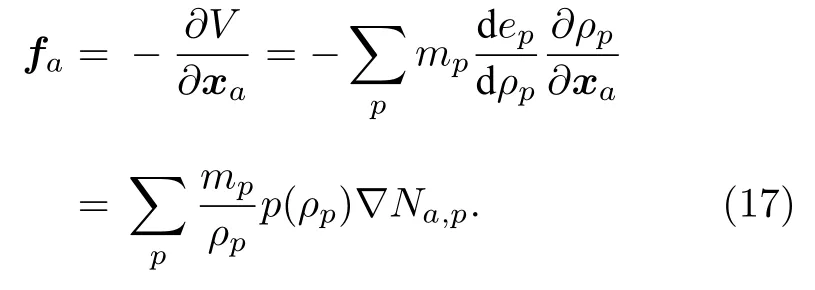
利用(12a)式、(14c)式和(14d)式得到

在(18)式中交換求和順序,拉格朗日方程變成:

其中,M為相容質量矩陣
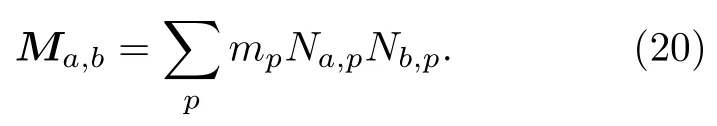
(19)式與更新拉格朗日有限元格式有兩點區別:1)有限元格式中的單元積分對應了OTM 中的粒子積分;2)有限元中使用基于網格的形函數,而OTM 方法中使用無網格的局部最大熵形函數.注意到局部最大熵形函數可以連續過渡到有限元線性形函數,因此,OTM 方法可以看成是一種特殊的單點積分拉格朗日有限元方法.
在有限元中方法,為避免矩陣求逆,常常將相容質量矩陣按行求和,得到集中質量矩陣,大大減少了計算量和存儲量,OTM 方法中同樣如此.利用形函數的單位分解性質,可以將粒子的質量分配給其相鄰的節點,得到如下節點質量定義:

注意到粒子質量和局部最大熵形函數都是嚴格大于零的,因此,節點質量也是嚴格大于零的.這樣連續介質既可以看成是粒子系統,也可以看成是節點系統.很明顯,這兩種系統的總質量和總動量都是嚴格相等的.
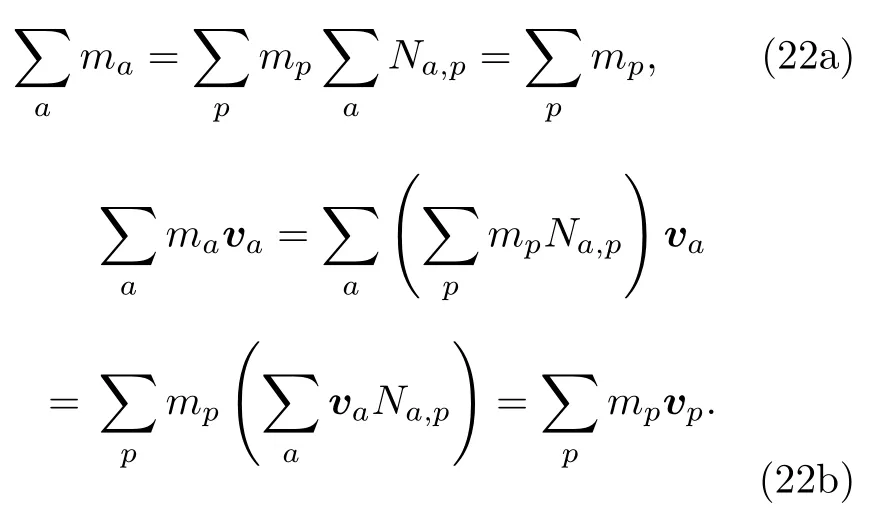
系統的總勢能通過粒子系統計算.系統的總動能既可以通過粒子系統計算,也可以通過節點系統近似計算:
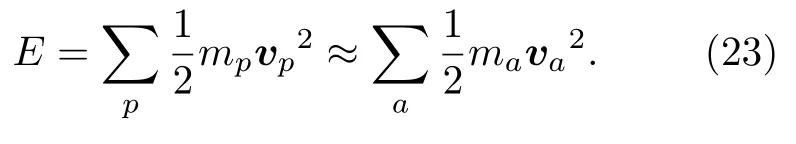
將(23)式代入(11)式,得到如下離散方程:

從(20)式和(21)式可知,節點質量剛好就是相容質量矩陣按行求和.利用節點廣義力和節點質量可以更新節點的速度和位置:
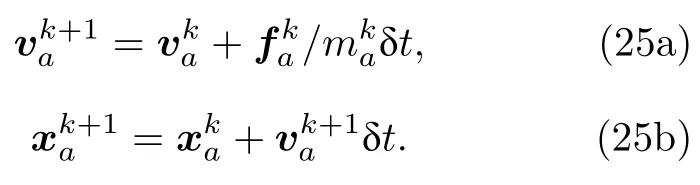
用(25b)式更新節點位置后,粒子位置根據(14a)式更新.注意到節點位置變化代表了流場的形變,因此兩個相鄰時刻的連續映射φ:xk →xk+1可以通過更新的節點位置插值得到
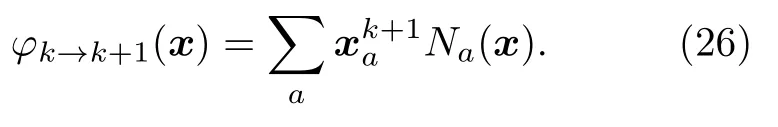
上述映射的梯度即為變形梯度張量:
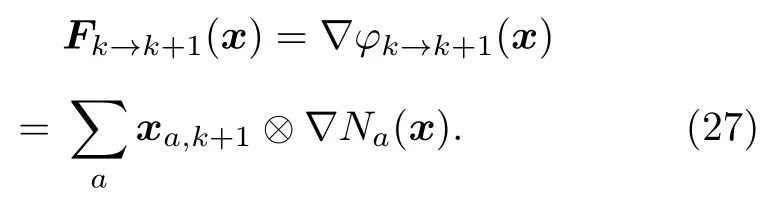
變形梯度張量的行列式在粒子位置處的值表征了粒子的密度變化
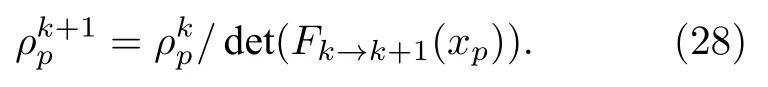
(28)式可以用于更新粒子密度.粒子密度更新后,根據物態方程更新粒子壓力.
2.3.1 流體黏性的處理
以上推導沒有考慮黏性,因而是保守系統.處理非保守力的基本想法將其看成外力,然后利用虛功原理推導對應的廣義力.假設fp是作用在粒子p上的外力,那么此力的虛功為

由虛位移的獨立性,得到相應的廣義力為
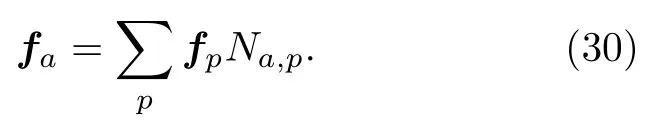
例如,作用在1個粒子上的重力fpmpg.根據(30)式得到廣義力考慮到重力實際上是保守力,因此也可以將重力勢能加入拉格朗日函數中,得到重力對應的廣義力.簡單計算可以證明兩者是一致的.
材料的很多行為(如彈塑性,黏彈性等)都可以統一用1 個應力張量描述,而應力張量的影響也可以看成外力,如下式中的動量守恒方程:
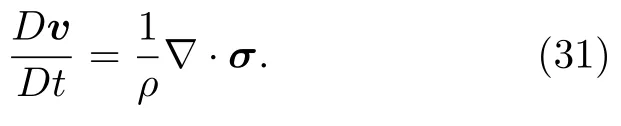
應力張量散度的物理意義為單位體積受到的力,因此,應力張量虛功為
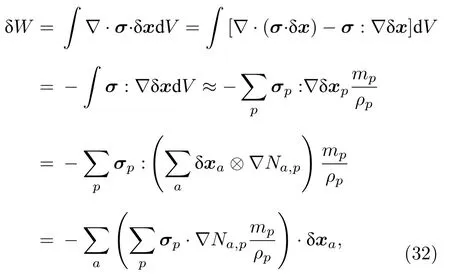
其中用到了高斯積分公式,并且假設了邊界上虛位移或者應力張量為零,這在固壁邊界以及自由表面邊界上都成立.同理,得到廣義力為

如果只考慮牛頓流體的黏性,那么黏性應力張量為

其中μ為黏性系數.
同理,(31)式也能通過勢能和拉格朗日方程得到.從(33)式可以看到,1 個粒子在無限短時間內受到的力只和應力張量本身有關,而和應力應變關系無關.因此,可以臨時假設1 個線性應力應變關系,從而得到簡單的彈性勢能.對彈性勢能求變分,就得到了相應的廣義力,詳細證明見附錄A.兩種方法的結果是一致的.
2.3.2 表面張力處理
考慮二維情況,液體邊界被邊界節點表征,如圖2 所示.
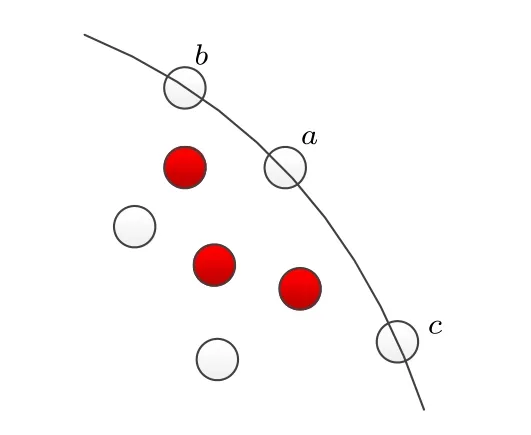
圖2 二維條件下的邊界節點(白點)Fig.2.Boundary nodes (white symbols) in two-dimensional coordinate.
表面勢能正比于表面積:
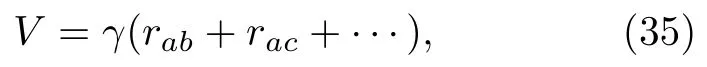
其中rab|xa-xb| ,rac|xa-xc| 為節點之間的間距.γ是表面張力系數.對(35)式求變分,得到廣義力
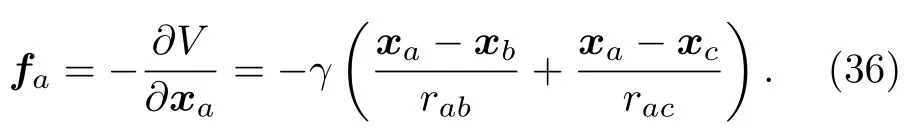
可以看到,(36)式非常簡潔,可以解釋為節點a同時受到兩個相鄰節點b和c的吸引力,吸引力大小剛好等于表面張力系數.(36)式中沒有可調參數,表面張力系數是唯一的輸入參數.此外,表面張力對應的廣義力只作用在表面節點上,即精確的作用在流體表面.
2.3.3 軸對稱處理
記(r,θ,h)為柱坐標系,并且假設環向沒有位移,而且所有物理量都和環向坐標無關,即 δuθ0,?/?θ0.定義:

那么,(11)—(14)式依然成立.速度矢量散度在柱坐標下的表達式為
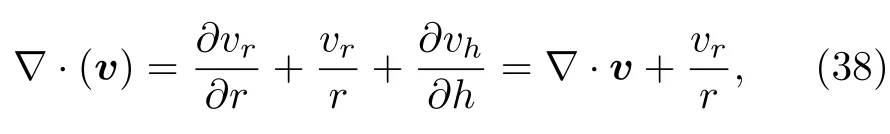
因此,粒子密度變化和粒子位置變化關系式(15)需要修改為
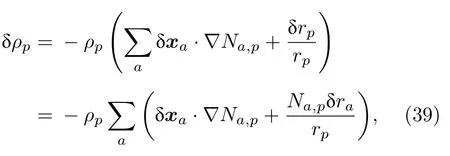
于是

其中nr是徑向單位向量.于是,軸對稱條件下的廣義力為
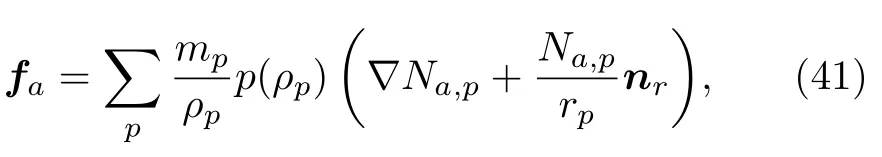
(18)—(26)式仍然成立.注意(27)式中的變形梯度張量的行列式表征的是粒子在(r,h)平面上的面積的變化:

因此,可以先更新粒子在(r,h)平面上的面積Sk+1,然后再更新密度:
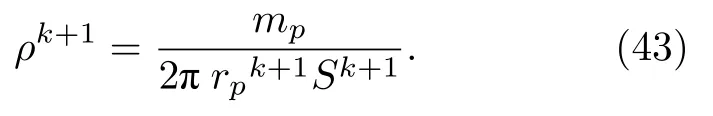
很明顯,外力對應的廣義力(30)式仍然成立.黏性力對應的廣義力也仍然成立,詳細證明見附錄B.
三維軸對稱條件下,表面勢能為
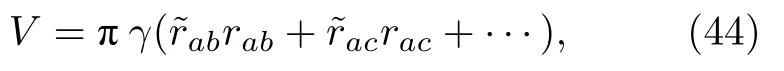

式中,前兩項為節點b和節點c對節點a的吸引力,后兩項為對稱軸對邊界節點的吸引力.可見,笛卡爾坐標系下的OTM 計算格式只需要經過微小改動,就能計算三維軸對稱問題.
2.4 OTM 方法詳細步驟
笛卡爾坐標系下,采用OTM 方法模擬表面張力的詳細步驟總結如下.
1)初始化:給定節點的位置和速度,給定粒子的位置和其他物理量.
2)近鄰粒子搜索:找到所有粒子-節點對.
3)對于所有粒子-節點對,計算形函數Na,p和形函數導數?Na,p.
4)計算節點質量、粒子速度梯度、黏性應力張量和廣義節點力:
5)更新節點速度和位置:
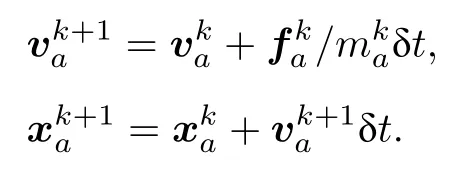
6)根據邊界條件調整節點位置,然后更新粒子位置:
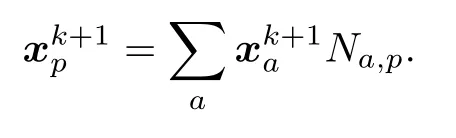
7)計算變形梯度張量并更新粒子密度和壓力:

8)完成1 個時間步長,回到步驟2).
3 典型算例
所有的初始化借助于有限元網格.網格節點變成節點,網格形心放置粒子,粒子體積即為網格大小.物態方程如下:
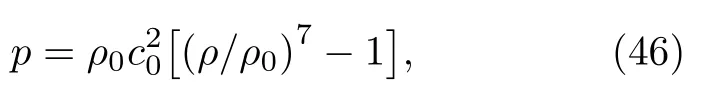
其中,ρ0表示材料初始密度,ρ表示當前密度,c0表示聲速,p表示壓力.
3.1 泊肅葉流
兩塊無限長的二維平板中間充滿了靜止液體,液體在平行于平板方向的體積力作用下開始運動,稱之為泊肅葉(Poiseuille)流.如果是無限長的三維圓管,那么稱之為Hagen-Poiseuille 流.對于二維泊肅葉,參數和文獻[24]一樣,解析解見文獻[24].將平板距離變成圓管半徑,即為Hagen-Poiseuille流,解析解見文獻[25].OTM 模擬結果見圖3.

圖3 速度分布的OTM 模擬與解析解對比 (a) 二維泊肅葉流;(b) 三維軸對稱泊肅葉流Fig.3.Comparison of OTM (symbols) and analytic solutions (solid curves) for velocity profile:(a) Two-dimensional Poiseuilleflow;(b) axisymmetric Hagen-Poiseuille flow.
OTM 模擬結果與理論解吻合很好.為了模擬無限長管道,用到了周期邊界條件.
3.2 靜止液滴
二維液滴的半徑R=0.2 m,密度ρ=1 kg/m3,表面張力系數γ=1 Pa·m,黏性系數η=0.5 Pa·s,聲速c0=50 m/s.靜止狀態下液滴的理論壓力值可以根據Young-Laplace 公式得到ρ=γ/R=5 Pa.如果是三維液滴,那么其理論壓力值為ρ=2γ/R=10 Pa.OTM 模擬的平均壓力分別為5.004 Pa 和 9.967 Pa.壓力分布如圖4 所示.

圖4 靜止液滴的壓力場 (a) 二維液滴;(b) 軸對稱三維液滴Fig.4.Pressure field:(a) Two-dimensional rod;(b) axisymmetric three dimensional drop.
由于弱可壓假設,壓力場中有誤差.但是液滴中的平均壓力非常接近理論值(誤差0.5%以內),證明了本方法的精度.
3.3 液滴的周期振蕩
在上1 個算例的基礎上,將黏性減小到η5×10-3Pa·s,并且附加1 個散度為0 的初始速度場vxx,vy-y給所有節點.二維液滴的理論振蕩周期為T[26].為了驗證OTM方法的收斂性,采用不同的粒子總數模擬這個問題,并且檢查兩條相互垂直線x0和y0 上的物理量分布,時刻tT/2,如圖5 所示.
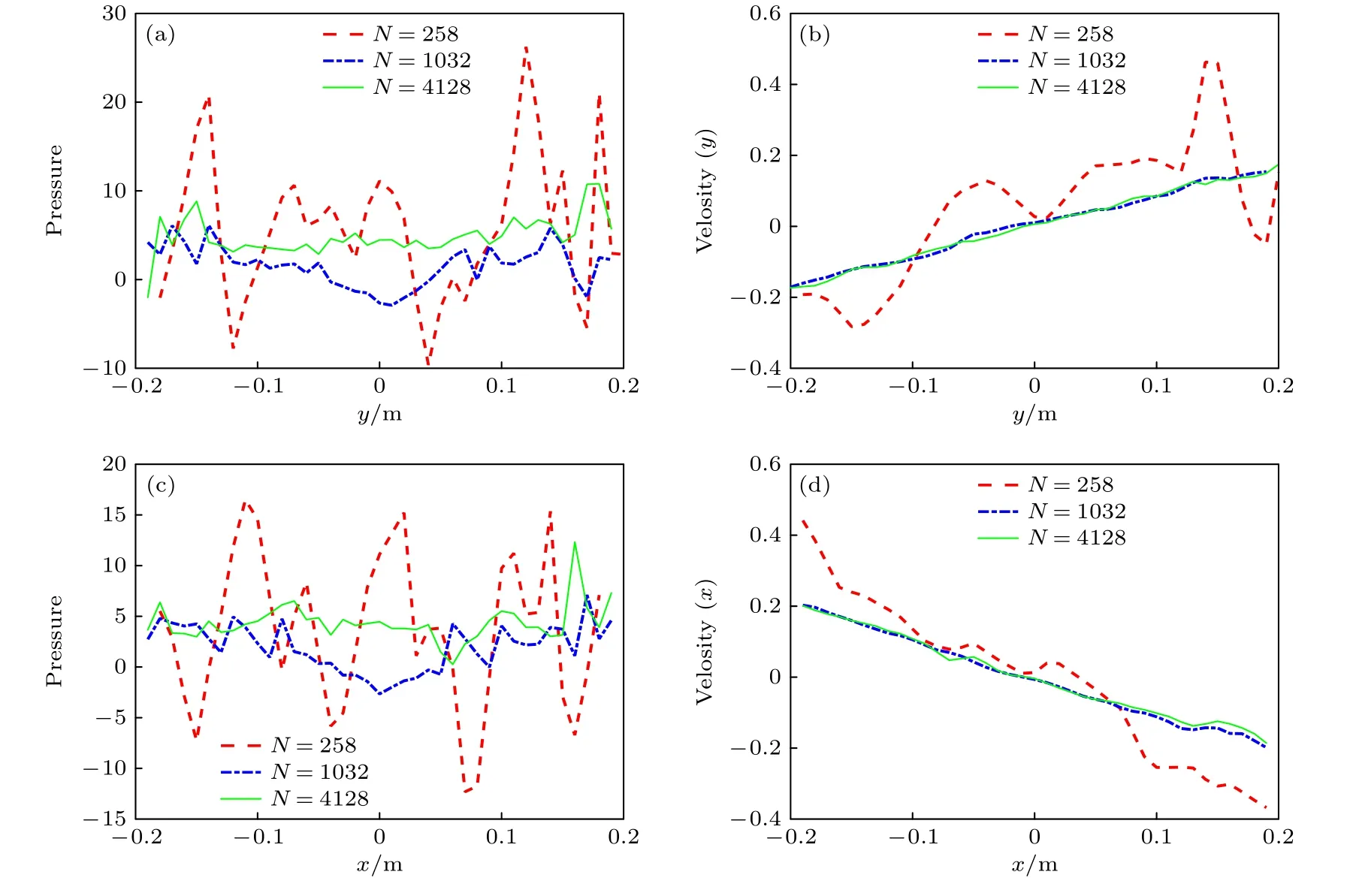
圖5 t=T/2 時刻的壓力和速度分布 (a) x=0 上的壓力分布;(b) x=0 上的速度分布;(c) y=0 上的壓力分布;(d) y=0 上的速度分布Fig.5.Pressure and velocity profile at t=T/2:(a) Pressure profile at x=0;(b) velocity profile at x=0;(c) pressure profile at y=0;(d) velocity profile at y=0.
可以看到,壓力分布的收斂不明顯,但是速度分布的收斂很明顯.改變表面張力系數的大小,得到的周期與理論值的對比如圖6 所示.周期是根據液滴右上部分質心軌跡測量得到,與文獻[26]一樣.
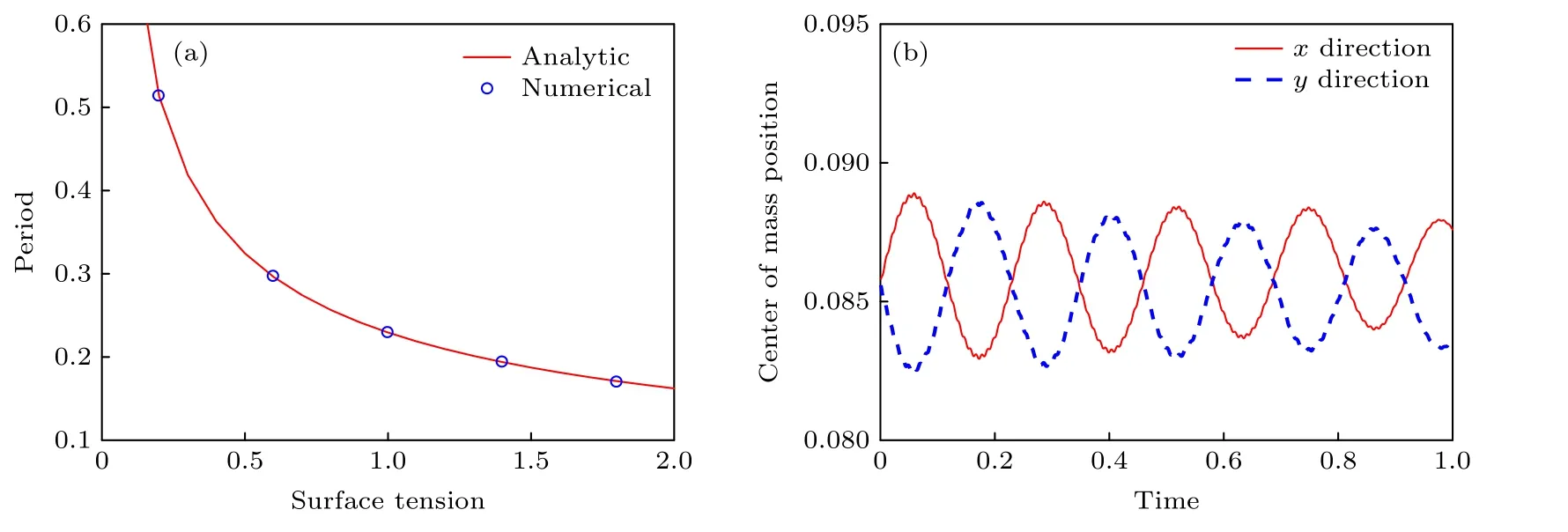
圖6 二維液滴振蕩 (a) 振蕩周期理論解和數值解得對比;(b) 表面張力系數為 γ=1 時液滴右上部分質心的軌跡Fig.6.Two-dimensional rod oscillation:(a) Comparison of period between the numerical (symbols) and analytical (solid curve) results;(b) center of mass position history when γ=1 .
對于軸對稱的三維液滴,散度為零的初始速度場取為vrr,vh-2h,其他物理量不變.振蕩周期的理論解為T[27].模擬結果與理論的對比如圖7 所示.模擬的周期根據對稱軸端點的位置軌跡測量.可以看到,兩種情況下OTM計算結果和理論非常吻合.

圖7 軸對稱三維液滴振蕩周期與理論的對比Fig.7.Three-dimensional droplet oscillation,comparing of period between the numerical (symbols) and analytical (solid curve) results.
3.4 液滴形變
將液滴半徑擴大到 1 m,表面張力系數擴大到10 Pa·m,加上大小為10 m/s2的重力.y=—1 m 處放置1 個光滑的固定平板.液滴在重力、表面張力以及光滑平板的共同作用下產生變形,如圖8 所示.
在圖8(d)中,壓力等值線與重力垂直,和理論相符.液滴內部的壓力場需要滿足兩個條件,一是壓力沿Y軸的線性分布規律 δpρgδY,另一個是自由表面附近的壓力滿足Young-Laplace 方程pγ/R.這兩個條件實際上決定了液滴的形狀,即液滴自由表面部分的微分方程為
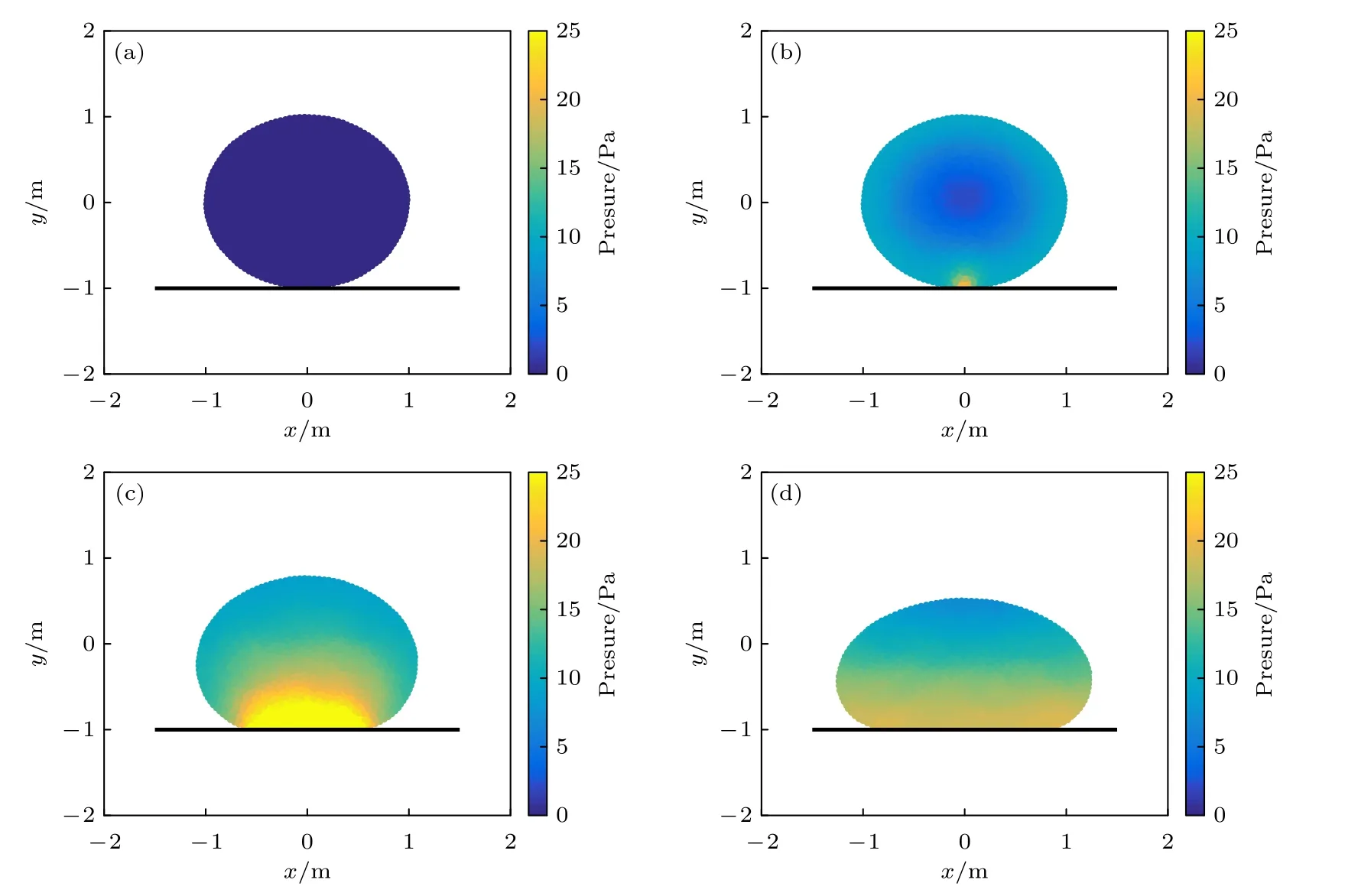
圖8 壓力場 (a) t=0 s;(b) t=0.02 s;(c) t=0.4 s;(d) t=4 sFig.8.Pressure field at several typical times:(a) t=0 s;(b) t=0.02 s;(c) t=0.4 s;(d) t=4 s.
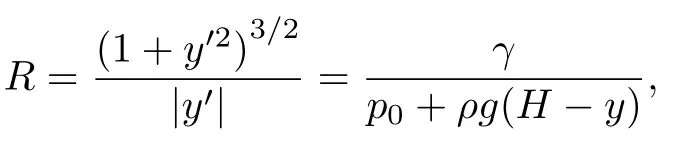
其中H和p0分別為液滴最高點的Y坐標和壓力.上述理論曲率半徑在實際計算時誤差太大,因此,本文采用如下方法計算曲率半徑:對于每個邊界節點,找到與其相鄰的4 個表面節點,然后用1 個圓來擬合這5 個節點,即自由變量為圓的中心坐標和半徑.圓的半徑即為此節點的曲率半徑.
液體中自由邊界的右邊部分如圖9(a)所示.采用曲率半徑計算的邊界壓力和根據EOS 計算的壓力比較如圖9(b)所示.
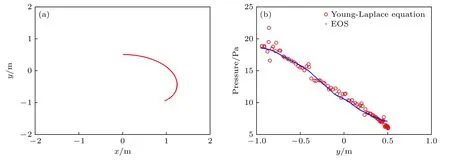
圖9 邊界位置和壓力 (a) 邊界位置;(b) 邊界壓力與Y 軸坐標的關系,壓力根據表面曲率和EOS 計算Fig.9.Boundary position and pressure profile:(a) Boundary position;(b) boundary pressure versus Y coordinate,computed by Young-Laplace equation (circles) and EOS (points).
兩種方法得到壓力值大致相等,說明模擬的自由表面形狀和理論相符.靠近固壁處誤差較大,經檢查是因為固壁附近節點的分布更加無序,導致搜索算法對初始參數敏感.壓力在Y軸方向的線性分布和理論相符,擬合直線的斜率也和理論dp/dY-ρg-10Pa/m 相符.
4 結論
本文基于拉格朗日方程,通過將表面張力勢能加入拉格朗日函數,得到了OTM 方法框架下的表面張力效應表達式,并且給出了軸對稱的處理方式.模擬了泊肅葉流,靜止和振蕩的液滴,液滴在重力、表面張力以及光滑平板共同作用下的形變等典型算例,通過與解析解對比,驗證了OTM 方法在模擬表面張力現象中具有如下優勢:1)表面邊界節點精確的表征了邊界的位置,保證了表面張力勢能的準確計算,而且表面張力對應的廣義力精確的作用在流體表面;2)表面張力對應的廣義力形式簡潔,具有直觀的物理意義,而且表面張力系數是唯一的輸入參數,不需要任何可調參數;3)可以保證速度分布的空間收斂性.
本文在連續介質離散時,節點和節點、節點和粒子之間沒有任何固定聯系,而是通過近鄰粒子搜索動態確定.但是,在計算表面張力勢能時,為了方便計算表面積,假設了表面節點之間的連接關系不變.因此,所有表面節點可以看成是1 個表面有限元網格.表面有限元網格與內部節點在拉格朗日方程框架下相互作用和協調運動.下一步,將考慮表面拓撲結構發生變化的情況,如多個液滴的融合過程.
附錄A 黏性應力張量對應廣義力的勢能方法推導
下面給出(33)式的勢能推導方法.將應力和應變張量寫成向量形式:
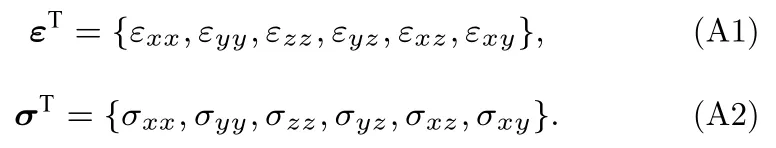
應變與位移的關系為

其中L是微分矩陣
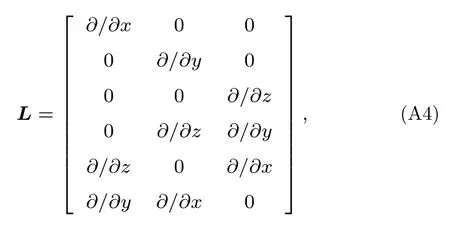
u是位移.廣義胡克定律為

其中c是1 個對稱矩陣:

以下4 個等式成立:
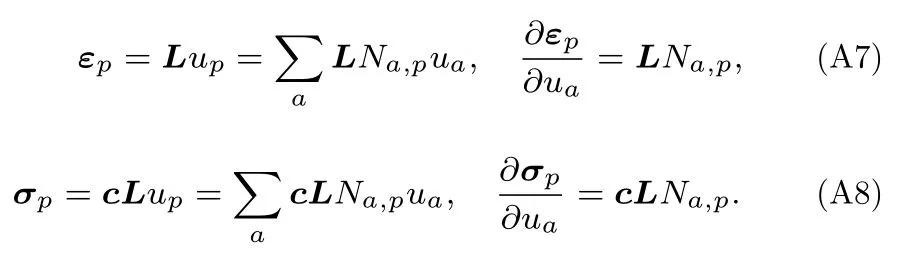
將(16)式寫成矩陣形式:

其中約定了形函數導數?Na,p為列向量.對于固定的應力張量σp,由于c可以取得足夠大,使得應變為小變形,于是彈性勢能為
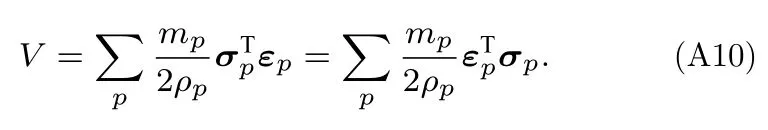
對彈性勢能求變分,得到

將向量形式改寫為常用的張量形式,得到

(A12)式第二項中有應變,因此是小量,可以忽略

(A13)式和 (33)式一致.
附錄B 軸對稱條件下黏性力對應的廣義力
兩個張量的雙點乘是1 個標量,因此,可以在柱坐標下求解
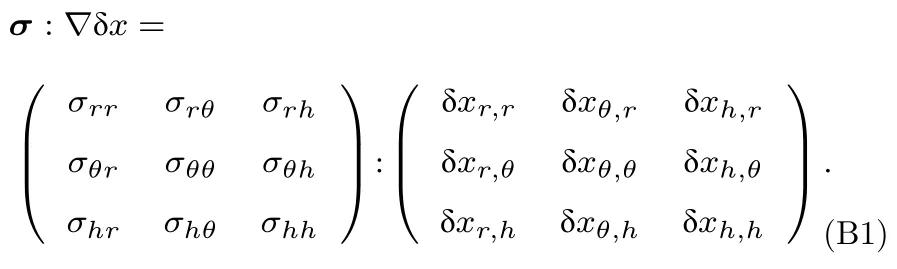
考慮到軸對稱,得到

利用定義(37a)式和(37c)式,虛功為
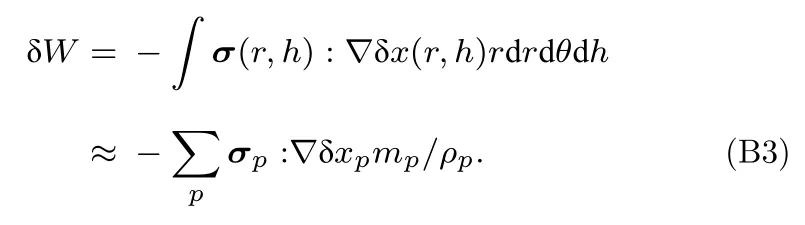
(B3)式與(32)式相同.

