環形泵浦激發下微腔激子極化激元的渦旋疊加態演化分析*

熊振宇 蔡遠文 吳昊3) 劉通3) 劉政良 任元3)?

1) (航天工程大學宇航科學與技術系，北京 101400)

2) (航天工程大學，量子探測與感知實驗室，北京 101400)

3) (航天工程大學，激光推進及其應用重點實驗室，北京 101400)

微腔激子極化激元由于具有較輕的有效質量，很容易實現玻色-愛因斯坦凝聚(Bose-Einstein condensate，BEC)，其在外界驅動下產生的陀螺效應具有廣闊的應用前景.本文研究了微腔激子極化激元在環形光束泵浦下微腔半徑以及泵浦參數對體系演化的影響.從單分量的Gross-Pitaevskii 方程出發，對環形微腔中的激子極化激元BEC 體系的演化過程進行研究.通過數值模擬研究了在環形微腔中保持體系穩定演化的最大渦旋疊加態花瓣數與微腔半徑的關系，分析了不同形式的環形光束泵浦作用下激子極化激元體系的演化情況，發現在微米量級的微腔半徑下，特定形式的單環泵浦和多環泵浦能夠使得微腔容納更高階的激子極化激元穩定渦旋疊加態的存在.研究結果表明，在一定的泵浦驅動條件下，微腔半徑的大小與體系能容納的渦旋疊加態花瓣數上限之間是線性正相關的，并且在改變泵浦激光構型時能夠突破這一上限，產生高階、多重的渦旋疊加態.

1 引言

激子極化激元是半導體微腔中激子和光子強耦合而形成的一種準粒子，既有光子的性質，同時也表現出粒子的相關性質，表現為玻色子，具體形態為半光半物質的雜化態.早在20 世紀 50 年代末，Hopfield[1]就提出了激子極化激元的概念，半個多世紀以來，尤其是微腔中的激子極化激元的研究，取得了令人矚目的成就[2-5].在實驗上對激子極化激元的反交叉色散行為進行了觀測[6]，觀測結果表明，微腔激子極化激元的有效質量非常輕，因此很容易實現玻色-愛因斯坦凝聚 (Bose-Einstein condensate，BEC).此外，微腔激子極化激元發生凝聚的臨界溫度可以達到幾開爾文，而且有可能實現更高溫度下的凝聚[7-15]，比如在基于GaN 的半導體微腔中實現了激子極化激元的室溫凝聚[16]，這是其他玻色子無法比擬的.在實際應用方面，微腔中的激子極化激元體系及其相關操控可以用于光電探測、光學開關、量子計算等領域[17-22].在此基礎上，激子極化激元體系的可操控性研究為探索未來工程應用提供了新的可能性.例如，基于激子極化激元 BEC 量子化渦旋構建的新型慣性器件在量子導航領域有著極大的潛在應用價值.本文正是在此基礎上，對激子極化激元BEC 新的潛在應用領域-新體制慣性器件中的幾個重要物理問題進行深入探究.

本文基于2019 年提出的一種基于BEC 中量子化渦旋疊加態為基礎的波-粒渦旋陀螺儀的科學設想[23].這種新體制的量子陀螺儀利用光與物質相互作用而形成的渦旋疊加態的激子極化激元凝聚為載體，以期產生陀螺效應，進而成為一種新型的高精度高靈敏度陀螺.同年，陳海軍等[24]對二維激子極化激元凝聚中渦旋疊加態穩態及動力學特性進行了研究，通過虛時和實時演化方法求解耗散Gross-Pitaevskii (GP)方程，研究了諧振子勢阱和高斯型勢壘疊加形成的類墨西哥帽子勢阱中正反渦旋疊加態的穩態結構，發現系統的泵浦、損耗和增益對系統的穩定性和動力學特性均有重要影響.2020 年，吳昊等[25]主要針對二維激子極化激元凝聚渦旋疊加態進行了動力學特性的分析，在體系旋轉的條件下，研究了渦旋疊加態激發區域的旋轉速率與體系旋轉速率的關系，并闡明了體系的旋轉速率對渦旋疊加態相位穩定性的影響機理，實驗研究了旋轉條件下的激子極化激元體系，更深層次地探究了激子極化激元凝聚的陀螺效應，將波-粒渦旋陀螺儀的研究推向了新的層次.

在此基礎上，本文對兩個影響體系特性的關鍵性參數進行了深入的研究，即微腔的尺寸和泵浦光束的構型.微腔的尺寸往往直接影響著集成器件的體積和功耗，此外傳播于微腔中的激子極化激元疊加態物質波的相干花瓣的數量與陀螺的精度和靈敏度息息相關，而微腔的大小對這種相干花瓣的數量有著直接的影響;同時，泵浦區域連續與否對體系演化也存在著關鍵性影響[26]，不同的泵浦構型會影響體系的演化.因此，微腔的尺寸以及泵浦的構型對量子渦旋陀螺儀的研究具有重要意義.本文以此為切入點，探究了微腔尺寸與泵浦激光構型對激子極化激元凝聚渦旋疊加態的影響.

本文從單分量的GP 方程出發，對環形泵浦光激發下的渦旋疊加態BEC 體系的激子分量隨時間演化的過程進行了數值模擬，并在此基礎上，分析了環形微腔的半徑與體系能容納的渦旋疊加態花瓣數上限的聯系，給出了它們之間的擬合關系;進一步地考慮一種復雜的情形，即用多個環形泵浦約束微腔中的激子極化激元，據此對這種情形下的物理過程進行了詳盡的分析，發現多環泵浦可以為微腔中激子極化激元BEC 渦旋疊加態帶來諸多改變，使其分裂、演化出更多的傳播模式.

本文的結構如下:第2 部分給出了選用的單分量GP 方程模型，以及泵浦激光的形式;第3部分研究了微腔半徑與能容納的最大渦旋疊加態的關系，并描述了其相關性;第4 部分給出了改變泵浦激光的構型而產生的多重、高階激子極化激元渦旋疊加態結果分析;第5 部分給出了微腔半徑和泵浦激光構型對激子極化激元體系演化影響的相關結論.

2 數值模型的建立

激子極化激元的產生基礎是光子與半導體微腔中的電子-空穴對的耦合與激發，對于激子極化激元的數值仿真，主要研究對象是半導體微腔中受激電子-空穴對的疊加態及其演化特性.基于此考慮選擇單分量的GP 方程模型[27]:

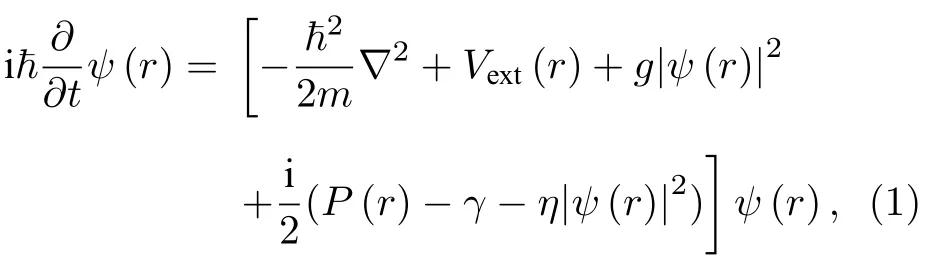
其中，波函數ψ(r)描述激子極化激元場;Vext(r) 為結構勢壘，表示玻色-愛因斯坦凝聚區域的勢阱;P(r)為泵浦項;g為激子極化激元間的非線性相互作用;γ為系統損耗項;η為激發飽和參數.其中，Vext(r) ，P(r) ，γ的量綱為meV，g和η的量綱為meV·m2.

為了方便計算各系統參數對陀螺效應的影響，建立GP 方程的數值模型，再根據此模型，對激子極化激元在不同初值和邊界條件下隨時間演化的過程進行計算和研究.下面對(1)式描述的方程做無量綱化處理，這里將場函數寫為ψ(r，θ，t)，并對其他參數做代換如下:

注意到(1)式中

將(2)式和(3)式代入(1)式后可得

通過調整系統差分步長、系統仿真總時間可以控制計算精度和迭代速度;通過調整泵浦光參數變量可以研究不同結構、不同強度的泵浦光對系統穩定性的重要影響.這里由于在(2)式中對時間t進行了無量綱的代換處理，因此在下文中時間t都帶有一個/meV 的量綱.數值計算中的每個單位時刻代換到典型實驗時間后為(1/meV)s，約等于6.5821×10-13s，也即 6.5821×102fs.

本文的計算采用環形激光對實驗區域進行激發，在環形激光泵浦激發的情形下，用

表示環狀泵浦激光，其中r為空間位置，r0為環的中心位置，ω0為環形泵浦的寬度，A表示泵浦激光的光強.

渦旋疊加態是由具有相同軌道角動量量子數的正反渦旋疊加形成渦旋疊加態，在諧振子系統中，渦旋型的基態解形式是高斯型，因此數值計算過程中，選用如下形式的高斯型渦旋疊加態函數作為疊加態初始解[24]:

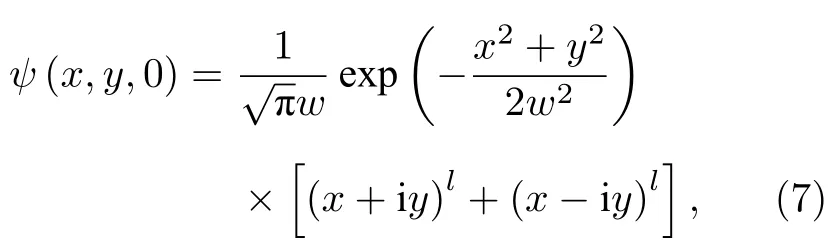
其中w表示初始波包的寬度，l表示渦旋量子數，根據l的不同取值可以構造出不同的渦旋疊加態，所形成的渦旋疊加態呈相互對稱的瓣狀，稱為“疊加態花瓣”，簡稱為“花瓣”.產生的“花瓣”個數稱為“花瓣數”，花瓣數與渦旋量子數l有關，為 2l.

3 微腔半徑與疊加態花瓣數的關系

微腔的尺寸往往直接影響著集成器件的體積和功耗，此外傳播于微腔中的激子極化激元疊加態物質波的相干花瓣的數量與陀螺的精度和靈敏度息息相關，而微腔的大小對這種相干花瓣的數量有著直接的影響.考慮在微腔大小不變的情況下，即計算區域一定，通過改變體系的期望疊加態花瓣數，分析體系的演化穩定性.實驗假設微腔區域為在二維平面上半徑為 5和10 μm 的同心圓所構成的環形帶，分別取渦旋量子數l3， 5， 8 對激子極化激元體系的演化進行分析，不同的渦旋量子數對體系總粒子數的影響如圖1(a)所示.

根據計算結果發現，計算時間t在0—100/meV范圍內，當l取值為3 和5 時，激子極化激元體系能演化至穩定狀態，即體系內的總粒子數不再發生變化;當進一步增加l，取l8 時，激子極化激元體系的總粒子數在短時間內達到穩定的基礎上將會出現波動，直到 100/meV 時刻總粒子數也沒有再次達到穩定.分別取t100/meV 時的計算結果作圖分析，3 種渦旋量子數對應的體系粒子數密度演化情況如圖1(b)—(d)所示.可以看出，對應于渦旋量子數l3和l5 時，體系最終可以演化為花瓣狀，在粒子數密度分布圖中清楚地分辨出有6 個和10 個花瓣;但渦旋量子數l8 時，粒子無序地分布在演化區域中，此種情況下，花瓣消失.出現這種情況的原因在于，在(1)式所描述的方程模型中泵浦項P(r)和耗散項γ決定了系統最終是一種動態平衡，其必然存在著一個漲落.在選擇了一定環形大小的情況下，“花瓣”數越多，系統中某處微小的不平衡就會使整體的振蕩變大，導致系統各處非線性能量產生的漲落也變大，進而影響了激子極化激元的穩定.

圖1 渦旋量子數 l=3， 5， 8時的計算結果 (a)激子極化激元體系在演化時間從0 到 100 /meV 的總粒子數變化圖;(b)，(c)，(d)渦旋量子數 l=3， 5，8時激子極化激元體系在 t=100 /meV 時的粒子數密度分布情況Fig.1.Calculated results of vortex quantum number l=3， 5， 8 :(a) Total particle number of exciton polariton system changes from 0 to 100 /meV in evolution time;(b)，(c)，(d) particle number density distribution of exciton polariton system at t=100 /meV with the vortex quantum number l=3， 5，8 .

隨后，改變微腔的半徑，將環形微腔的區域從之前的 5—10 μm改為15—20 μm (下文稱之為“大半徑”模式).在此種情況下，微腔的寬度沒有改變，但環的半徑增大.如圖2 所示，當渦旋量子數l8時可以演化至穩定狀態，密度分布中出現了 2l即16 個花瓣，且體系的總粒子數密度曲線最終也保持穩定.

圖2 大半徑下激子極化激元體系在 l=8時的演化圖像 (a) t=100 /meV時，體系的粒子數密度分布;(b)t=100 /meV時刻之前體系總粒子數的演化情況Fig.2.Evolution image of the exciton polariton system with a large radius at l=8 :(a) Particle number density distribution of the system at t=100 /meV;(b) evolution of the total particle number of the system before t=100 /meV .

據此認為，在增大環形微腔半徑下，環形微腔能夠容納的最大疊加態花瓣數也會隨之增大.也就是說，激子極化激元體系能容納的最大疊加態花瓣數與環形微腔的半徑是正相關的.為了進一步驗證這個猜想，在下面的計算中設置環形微腔的寬度為5 μm 保持不變，不斷改變環形微腔的內半徑的大小，計算得出在不同內半徑大小的情況下，激子極化激元體系能夠容納的最大花瓣數，具體結果如圖3 所示.

通過圖3(a)的數據散點圖及其擬合曲線可以清晰地看出，在保持其余參數不變的情況下，激子極化激元體系中能容納的最大花瓣數與環形微腔的內半徑是呈線性正相關的.因此得出結論，環形微腔在泵浦光的激發下能夠產生渦旋疊加態的花瓣，花瓣能夠穩定存在，但一定半徑的環形微腔能夠“容納”的渦旋量子數是有限的，當渦旋量子數過大時，系統將會失穩，無法支持形成穩定的花瓣;但隨著環形微腔半徑的增大，環形區域能容納的激子極化激元體系的疊加態花瓣數也會增大，激子極化激元體系中能容納的最大花瓣數與環形微腔的內半徑呈線性正相關關系.而對應于量子渦旋陀螺儀的實際應用場景，這些包含著軌道相位信息的疊加態花瓣越多，依賴于相位信息檢測方法所測得的精度和靈敏度都將得到提高.

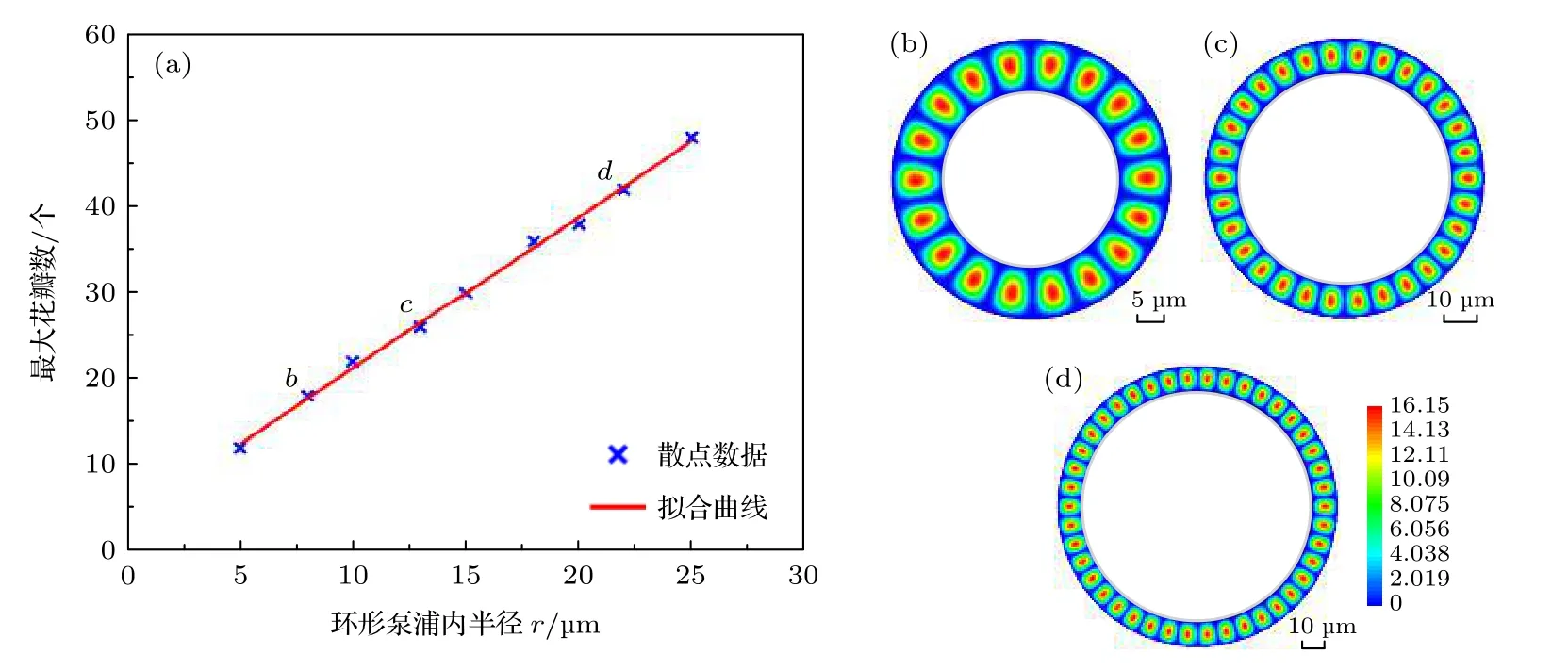
圖3 在改變環形微腔半徑后，計算分析得到的對應體系下的最大承載花瓣數 (a)環形泵浦半徑與能容納的最大花瓣數的關系，環形微腔寬度統一為 5μm，橫坐標是環形微腔的內半徑，縱坐標是能夠容納的最大花瓣數.點b，c，d 分別是圖(a)中的3 個取值點，對應的環形微腔內半徑分別為 8，15 和 22 μm.(b)，(c)，(d) 3 個取值點在演化時間 t=100 /meV 時的粒子數密度分布.Fig.3.After changing the radius of the annular microcavity，the calculated maximum number of bearing petals in the corresponding system.(a) Relationship between the annular pumping radius and the maximum number of petals that can be accommodated.The width of the annular microcavity is 5μm，the abscess is the inner radius of the annular microcavity，and the ordinate is the maximum number of petals that can be accommodated.Points b，c and d are the three value points in panel (a) respectively，which correspond to the radii of the annular microcavity of 8，15 and 22 μm respectively.(b)，(c)，(d) Particle number density distribution of the three value points at evolution time t=100 /meV .

4 泵浦構型對激子極化激元體系演化的影響

在環形微腔中形成激子極化激元體系時，一般采用泵浦光對系統全域提供能量，但在實際情況中，微腔中可能會通過構造掩膜的方式人為地構造出不同的環形微腔，例如多個環帶中的激子極化激元體系的演化，以此下面通過設置泵浦構型的方式來探究泵浦區域對體系的演化影響.

4.1 改變徑向寬度后的單環泵浦對渦旋疊加態演化的影響

首先考慮到在實際演化中，泵浦區域與實驗區域不一定會嚴格匹配，比如，泵浦區域與實驗區域存在偏心、泵浦區域不能完全覆蓋實驗區域等特殊情況，這些在實際操作中是極有可能出現的.這里對泵浦區域不能完全覆蓋實驗區域這種情況進行分析.在數值計算中設置實驗區域與之前不變，仍為二維平面上 5—10 μm 的環形區域，環形泵浦區域從 5μm 開始，泵浦寬度設為變量，其余參數保持不變，以此來研究泵浦的徑向寬度對激子極化激元體系演化的影響.數值模擬發現，當選擇泵浦區域為 5—7.5 μm 的情況時，激子極化激元體系的演化會出現高階花瓣態，實驗結果如圖4(d)所示，可以看出，在徑向方向上，花瓣態一共出現了兩層，每層有18 個花瓣，花瓣數達到了此前演化穩態時的3 倍.

對這種演化的過程進行分析，在演化開始，即t0/meV時(圖4(a))，體系為初始態;當t60/meV時(圖4(b))，激子極化激元體系的演化與之前的穩態相比已經出現變化，相較于圖4(a)中花瓣數為6 的初態，這里的每個花瓣出現了分裂;當t100/meV 時(圖4(c))，內外層各18 個花瓣都已出現雛形，但每個花瓣的強度分布還沒有演化穩定，因此存在著強度上的差異;隨著體系的進一步演化，當t160/meV 時(圖4(d))，激子極化激元體系演化至穩態，對比于圖1(b)中花瓣數為6 的穩態，此時不僅出現了花瓣數高達18 的高階形態，而且在徑向方向上出現了兩層激子極化激元的凝聚.同時相較于圖4 中計算得出的數據，在環形泵浦半徑為 5—10 μm 時，體系能容納的最大花瓣數僅為12，而這里的體系中穩定存在了18 個花瓣，這一發現對進一步提高環形微腔中的花瓣數提供了新的思路.

圖4 泵浦區域為5—7.5 μm的單環泵浦下體系的演化過程，即(a) t=0 /meV，(b) t=60 /meV，(c) t=100 /meV，(d) t=160 /meV 時體系的粒子數密度圖Fig.4.Evolution of a single-loop pumping system with a pumping region of 5-7.5 μm .Panels (a)，(b)，(c) and (d) correspond to the particle number density diagram of the system at t=0 /meV，60 /meV，100 /meV and 160 /meV，respectively.

4.2 基于多環泵浦的渦旋疊加態演化分析

下面在泵浦區域不連續情況下，分析泵浦激光對體系演化的影響情況.通過人為地構造出空白的泵浦間隙環帶(以下簡稱“空環帶”)來改變泵浦的區域，以此來構造出所謂的雙環泵浦、三環泵浦等.比如，在泵浦區域內構造出一個空環帶，即可構造出雙環泵浦.由此類推，設置不同數量的空環帶，即可對泵浦區域進行構造，以達到使用多環泵浦對實驗區域進行演化分析的研究.

這里選取環形微腔的半徑仍為二維平面上5—10 μm的環形區域，渦旋量子數取l3，其他參數與前述中的計算保持不變，分別構造了單環、雙環、三環和四環的泵浦區域對渦旋疊加態的演化進行分析，實驗中設定泵浦服從(2)式中的環形泵浦分布，3 種泵浦的強度相同，其余參數條件與圖1(b)的計算條件相同，計算得出的結果如圖5 所示.

由圖5 可以看出，當設定不同環數泵浦區域進行計算時，最終的演化穩態基本保持著6 個花瓣數.其中，在雙環泵浦情況下，6 個花瓣內部各出現了兩處密度極大值和兩處密度極小值.在三環泵浦和四環泵浦的情況下，每個花瓣態按照徑向分為了3 個或者4 個較小的花瓣態，同一徑向上的密度分布規律同單環下的計算結果類似.

對圖5 的結果分析發現，雙環泵浦下的激子場演化相較于其他3 種泵浦有明顯的差異，此處產生的現象與2014 年Dreismann 等[26]的研究結論相似，Dreismann 等在雙環泵浦下，通過構造結構勢壘，將激子極化激元限制在微腔中并產生凝聚，與本文類似的是，實驗觀察到的激子極化激元凝聚發生在雙環泵浦中間的空環帶，而本文計算中亦是在空環帶上發生了與施加泵浦的區域不同的現象.因此下面對雙環泵浦情況進行深入分析，接下來改變泵浦區域的徑向寬度，即空環帶的大小，其余參數保持不變.以計算區域徑向中心為空環帶徑向中心，不斷改變空環帶的徑向寬度，部分數值計算結果如圖6 所示.

圖5 多環泵浦下的渦旋疊加態演化情況，圖(a)，(b)，(c)，(d)分別表示單環、雙環、三環、四環情況下的計算結果，其中第一行為構造的多環泵浦區域示意圖，紅色區域表示泵浦區域，白色區域表示構造出的空環帶;第二行對應于多環泵浦下體系演化的粒子數密度分布，取值時刻為t=100 /meVFig.5.Evolution of vortex superposition state under multiloop pump.(a)，(b)，(c) and (d) show the calculation results of singlering，double-ring，three-ring，and four-ring respectively.The first shows the schematic diagram of the multi-ring pumping region constructed，with the red region representing the pumping region and the white region representing the empty ring zone constructed.The second row corresponds to the particle number density distribution of the system evolution under the multi-loop pump，and the value time is t=100 /meV .

由計算結果可以看出，當空環帶的寬度增加，雙環泵浦的寬度降低時，如圖6(a)所示，激子場最終將演化為類似于三環泵浦的粒子數密度分布;而當空環帶的寬度降低，雙環泵浦的寬度增加時，如圖6(c)所示，激子場最終的演化結果類似于單環泵浦下的粒子數密度分布，推測是由于空環的寬度較低，空環的出現相較于沒有空環的情況接近，最終的結果才會出現與單環泵浦類似的演化終態.進一步分析發現，圖6(a)情況下的計算結果與Dreismann 等[26]的研究更為類似:即在雙環泵浦下，在空環帶區域產生了激子極化激元凝聚.而且與Dreismann 等的研究不同的是，本文的計算結果表明，在雙環泵浦的區域上也產生了激子極化激元的凝聚，所以在徑向上可以明顯看到有3 層“花瓣”的存在，而Dreismann 等的結果顯示雙環泵浦的區域中沒有產生凝聚現象，最終結果也只是在徑向上顯示了1 層的凝聚現象.此外，圖6(b)中的特殊演化模式的出現有很大的可能是環與環之間的物質波在徑向發生了干涉，形成了新的干涉極大區域，從而出現了這種特殊的演化結果.此處的計算結果顯示，雙環泵浦之間的空環帶寬度對這種演化模式的出現有著極大的影響，除此以外，使用的雙環泵浦內外環泵浦寬度相同，當設置內外環泵浦寬度不同時，亦有可能會對體系演化產生影響，這種多參數影響下的演化結果還有待進一步的研究.

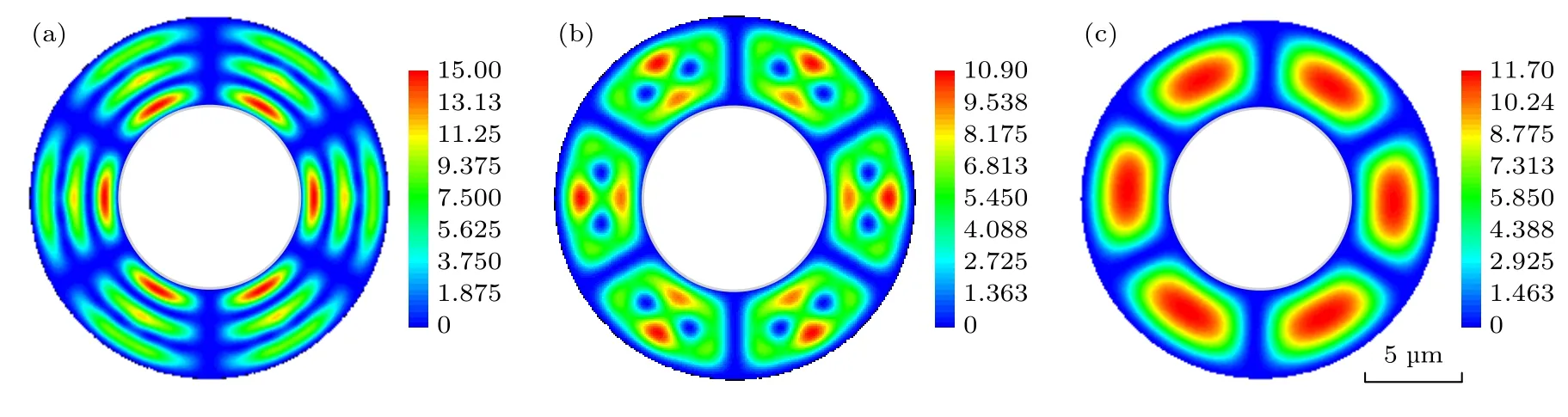
圖6 不同空環帶寬度下雙環泵浦時激子場演化的分析，圖(a)，(b)，(c)分別對應于空環帶區域為 6.6—8.4 μm，6.9—8.1 μm 和7.2—7.8 μm時體系演化的粒子數密度分布，取值時刻為t=100 /meVFig.6.Analysis of the evolution of exciton field under double-ring pump with different void band widths.(a)，(b) and (c) correspond to the particle number density distribution of the system evolution when the void band region is 6.6-8.4 μm，6.9-8.1 μm and 7.2-7.8 μm respectively，and the value time is t =100 /meV .

5 結論

本文利用一個單分量的GP 方程對環形微腔中的激子極化激元體系進行仿真計算，分析數據發現，在保證其他參數一定的情況下，一定大小的環形微腔對激子極化激元疊加態花瓣的承載量是有限的，強行讓微腔承載較大的疊加態花瓣數只會使激子極化激元體系不能演化穩定;而在增大環形微腔的半徑后發現，體系對疊加態的花瓣數的承載上限將得到提高.多次計算取得大量數據后得出結論:其他條件不變時，大半徑的環形微腔能夠容納更多的疊加態花瓣，能夠承載的最大花瓣數與環形微腔半徑成正比.而這些疊加態花瓣包含著大量的密度以及相位信息，依賴這些信息檢測可以獲得體系的外部運動信息.因此，更大的環形微腔半徑能夠產生更多的花瓣數，更多的花瓣數代表著測量精度與靈敏度的提升;但是微腔的半徑越大，所形成的器件體積也會越大，由于體積的增大有可能進一步帶來系統的失穩等，因此實際運用中還將在體積與精度之間選擇合適的方案.

除以之外，本文還分析了環形泵浦的構型對體系演化的影響.計算發現，在一定的徑向寬度下單環泵浦可以激發體系產生高階的渦旋疊加態花瓣，實驗采用相同的微腔參數，僅改變單環泵浦的徑向寬度，最終得到的花瓣數是未改變徑向寬度前的3 倍，此種情況下的疊加態花瓣數不僅超出了之前計算得出的環形微腔在此半徑下能容納的最大花瓣數，而且在徑向上出現了多重花瓣組合，這一發現對進一步提高環形微腔中的花瓣數提供了新的方向.本文還構造了多環泵浦對環形微腔區域進行計算，計算結果表明，在三環、四環泵浦下，體系的演化最終呈現出徑向方向的多重花瓣態;在雙環泵浦下體系下改變空環寬度不僅可能會在空環帶中出現新的激子極化激元凝聚，而且有可能在原本的每個花瓣中出現新的渦旋態，這些渦旋態對應的相位信息表明其也產生了激子極化激元的凝聚現象，這些特殊的演化結果為新體制陀螺的研究開拓了新的方向.