一種基于攝動理論的不連續系統Lyapunov 指數算法*

馬召召 楊慶超 周瑞平

1) (武漢理工大學能源與動力工程學院，武漢 430063)

2) (海軍工程大學艦船與海洋學院，武漢 430033)

Lyapunov 指數是識別系統非線性動力學特征的重要標志，但是目前的算法通用性不足且計算流程復雜.本文在經典的Lyapunov 指數算法的基礎上，基于攝動理論提出了一種適用于不連續系統的Lyapunov 指數計算方法.首先，以系統狀態參數初始值和沿相空間每個基本矢量的擾動量為初始條件，確定相軌跡.其次，采取差商近似導數法，獲得Jacobi 矩陣的近似矩陣.然后，對Jacobi 矩陣進行特征值提取，得到系統的Lyapunov 指數譜.最后，將新算法應用到二自由度干摩擦沖擊振蕩器系統實例中，并將計算結果與同步方法的計算結果進行對比，對新算法的有效性進行驗證.該算法不僅適用于離散系統和連續時間系統，而且能夠快速計算復雜不連續系統的Lyapunov 指數，為確定復雜不連續系統的動力學行為提供了新思路.

1 引言

Lyapunov 指數是在局部和全局穩定性準則下確定系統穩定性的數值，它表征了系統在相空間中相鄰軌道間收斂或發散的平均指數率[1].從數學角度，Lyapunov 指數是狀態轉移矩陣的特征值，決定了系統吸引子上軌跡無窮小擾動的演化進程.因此，Lyapunov 指數被認為是衡量系統對初始條件敏感性的重要指標.所有Lyapunov 指數值的和決定了系統在相空間中體積的發散度，所有Lyapunov指數值的和為負值是存在全局穩定吸引子的充要條件，并且表明系統是耗散的;若所有Lyapunov指數均為負值，則吸引子為穩定點;對于n維系統，如果前m個Lyapunov 指數等于零而另外n—m個Lyapunov 指數均為負值，則吸引子為m維環面;若最大Lyapunov 指數為正值，則為混沌運動，若存在不止1 個Lyapunov 指數為正值，則為超混沌運動.對于保守系統，所有Lyapunov 指數值的和為零，若所有Lyapunov 指數值的和為正值，則表明系統是全局不穩定的，相軌跡呈指數發散.

Benettin 等[2]及Shimada 和Nagashima[3]首先提出了1 個基于Oseledets 定理[4]計算Lyapunov 指數譜的有效算法，文獻[5-8]對算法進行了改進.近年來，提出了基于系統擾動的數量積和導數計算Lyapunov 指數的方法[9-13]，該算法可以計算連續系統的Lyapunov 指數譜，但是如果系統中存在不連續性則會出現較大誤差或數值溢出現象.

為了確定具有沖擊或干摩擦的機械系統、分段線性特性電振蕩器等不連續系統的Lyapunov 指數，可以采用等效的連續函數近似不連續分量[14]、最小二乘陰影法[15]和偽軌道法[16]消除狀態擾動矢量的不連續性等方法，雖然不需要重構相空間和Jacobi 矩陣，但容易引起系統動力學特性的質變.Takens[17]和Wolf 等[18]根據時間序列信號重構系統吸引子，提出了計算不連續系統最大Lyapunov 指數的算法.多年以來，文獻[19-27]針對該類方法的數據量、穩定性和計算速率等方面進行了評估改進，該類方法的優點是物理意義明顯，便于理解，計算結果不易受到拓撲復雜性的影響，有一定的抗噪能力.近年來，部分學者又提出了映射法[28-30]、補償矩陣法[31]、完全同步法[32-36]、克隆動力學法[37]等，這些方法對一些特性類型的不連續系統具有較高的準確性，但算法通用性不強且計算流程較為復雜.

本文提出了一種計算不連續系統Lyapunov指數譜的新方法.該方法基于攝動理論，使用正交矢量型初始擾動計算Jacobi 矩陣，對Jacobi 矩陣進行特征值提取，得到系統的Lyapunov 指數譜.該方法僅需要選定初始條件，無需確切知道系統的方程式，便能夠確定系統的最終狀態，而且對不連續系統和連續系統均適用.

2 方 法

為了克服現有Lyapunov 指數算法的不足，以一般性的理論為依據，使得新算法適用于更多的系統并更具通用性;另一方面，以經典的數值算法為基礎，對廣泛應用的Jacobi 法進行改進，保證新算法計算的準確性.

2.1 算法理論

以常微分方程(ODE)形式描述一種n維自治連續時間系統:

其中，x ∈Rn為狀態向量，t ∈R為時間，f為Rn →Rn上的連續可微函數.假設St(x0) 為滿足ODE(1)初始條件x0的解(軌跡)，則有

Lyapunov 指數的定義是基于以下Jacobi 矩陣建立的:

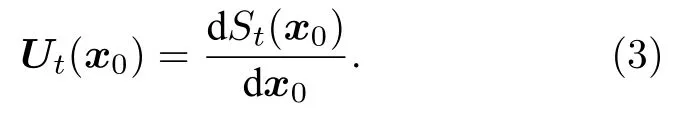
(2)式對x0進行微分獲得如下變分方程:

矩陣Ut(x0) 顯示了初始條件x0的無窮微擾對軌跡St(x0)的影響:

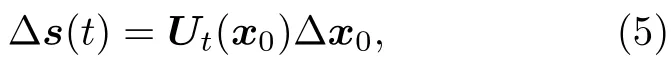
其中Δs(t)是由初始擾動量Δx0引起St(x0) 的擾動，即: Δs(t)St(x0+Δx0)-St(x0) .向量Δs(t)的長度可以從下式中求得

令ui(t)，i1，···，n為Ut(x0)TUt(x0)的特征值.Ut(x0)是1個實矩陣，所以Ut(x0)TUt(x0) 是實對稱的.因此，ui(t)∈R和對應的特征向量可以構成正交基vi(t)，i1，···，n.由于任意1個Δx0∈Rn，都有 |Δs(t)|2≥0，可得到矩陣Ut(x0)TUt(x0)為半正定，且ui(t)≥0.因此，如果Δx0與vi(t) 平行，則 |Δs(t)||Δx0|可以得到:若初始擾動量Δx0的1個分量與vi(t) 平行，則其軌跡長度的影響因子為可用以下公式表示:

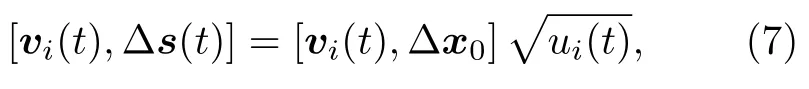
其中 [a，b]表示向量a，b之間的數量積.

Lyapunov 指數的定義為

從(8)式可以得到，在時間t足夠長的情況下，

因此，對于每個Lyapunov 指數值λi，在相空間中都存在1 個對應的方向，使得初始擾動量Δx0在該方向上的投影長度乘以 eλit作為系統在時間t內的演化.可用以下公式表示:

這意味著每個Lyapunov 指數是初始擾動量Δx0的分量沿相空間某個方向的平均指數收縮率(如果λi ＜0)或擴展率(如果λi ＞0).

Lyapunov 指數的概念不僅適用于連續時間系統，而且適用于離散時間系統.上述理論為連續時間和離散時間系統提供了Lyapunov 指數計算的一般方法.首先，對于足夠長的時間t，使用(4)式計算Jacobi 矩陣Ut(x0) ;然后，計算Ut(x0)TUt(x0)的特征值ui;最后，應用(8)式計算每個Lyapunov指數值.

2.2 連續系統經典算法

基于以上推導公式建立了一種連續系統的經典算法[8].該算法利用了最大的擾動子空間Wi中的每個初始擾動均以 eλit的速度變化這一特點，即平行于vi的初始擾動量Δx0分量的長度在時間t上以因數 eλit進行擴展或收縮.

假設n維系統的Lyapunov 指數λ1≥λ2≥···≥λn，幾乎任意1 個初始擾動量 Δx0都具有與v1平行的分量，則該分量長度的變化因數為 eλ1t.如果λ1是最大Lyapunov 指數，則其分量將成為主導量.由于擾動量 Δx0的方向與v1對齊，則 Δx0的長度以近似指數速率λ1變化，即 |Δs(t)|≈|Δx0|eλ1t.這意味著λ1決定了幾乎所有初始擾動改變其長度的平均指數速率.為了計算n個Lyapunov 指數譜，通過Gram-Schmidt 正交歸一化獲得相互正交的初始擾動量 Δx，減少擾動量之間對齊的影響.為了計算λ2，當 Δx0與v1對齊時，必須計算另1 個與 Δx1正交的新擾動，且該擾動的長度以近似指數速率λ2變化，并與v2對齊，如圖1 所示.

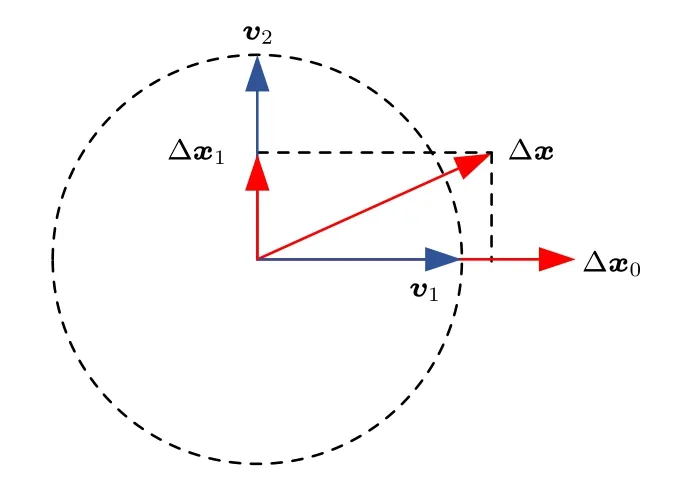
圖1 兩個擾動量 Δx，Δx0 的正交歸一化Fig.1.Orthonormalization of two perturbations Δx， Δx0 .

以此類推，為了計算λ3，必須計算1 個與前面兩個擾動量正交的新擾動，則其與v1和v2正交，以近似指數速率λ3變化，并與v3對齊.總的來說，若計算n個Lyapunov 指數譜，必須計算n個不同的擾動，第1 個是根據等式(5)自由演化的，其他第i個新擾動都與第 1，···，(i-1) 個擾動量保持正交.

該算法唯一的約束是正交向量必須與原始向量跨越相同的擾動子空間.同時，由于矩陣Ut(x0)在時間t較長的情況下變得計算困難，甚至無法計算，使得該經典算法在實踐中效果不佳.

2.3 不連續系統Lyapunov 指數的算法

2.3.1 算法思想

在連續系統Lyapunov 指數經典算法[8]的基礎上，基于算法理論詳述利用差商近似導數法獲得Jacobi 矩陣計算不連續系統Lyapunov 指數的具體算法.

算法思想:首先設定初始條件x0和計算參數;然后求解系統，得到充分接近實際系統吸引子的軌跡;再利用差商近似倒數方法計算不連續系統的Jacobi 矩陣;利用Gram-Schmidt 正交歸一化獲得相互正交的初始擾動量，并將不同的擾動量用于求解相應的Lyapunov 指數，進而得到系統的Lyapunov 指數譜.

2.3.2 算法實現的具體方法

下面詳述該算法在不連續系統中實現的具體方法.

對于連續系統，方程(1)中的矢量場f在相空間軌跡的任意點x處是連續可微分的，利用經典算法[8]可以得出系統Lyapunov 指數.否則，不能直接從變分方程(4)獲得Jacobi 矩陣Ut(xj) .針對不連續系統，進行適應性修改.首先考慮連續時間不連續系統，系統(1)的解St(x) 實際上是將初始狀態x轉換為時間t之后系統(1)狀態的映射.Ut(x)為在點x處求得軌跡St的Jacobi 矩陣:

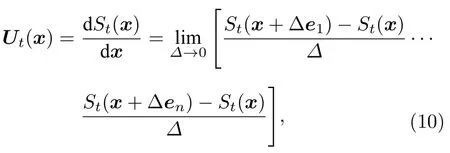
其中e1，···，en是Rn中的標準基，Ut(x) 的 列 是St(x)關于后續狀態變量的偏導數.根據導數定義，(10)式中的偏導數可以表示為Δ→ 0 時差商的極限.因此，可通過以下方式估算矩陣Ut(x) :

在選擇Δ值時，需要在與Δ成比例的截斷誤差和取決于實際使用數據類型的近似誤差之間取得平衡，矩陣Ut(x) 的近似算法如圖2 所示.

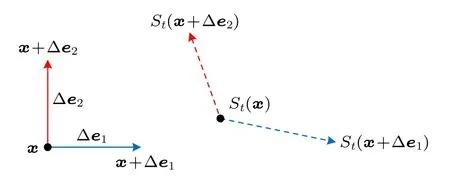
圖2 矩陣 Ut(x) 逼近算法示意圖Fig.2.Illustration of the algorithm of the Ut(x) matrix approximation.

為了估計Jacobi 矩陣Ut(x)，需要利用未擾動的初始條件x以及沿著相空間的每個受Δ值擾動的初始條件x+Δei，i1，···，n，確定映射St(x)的值.總之，估算一次矩陣Ut(x)，需要對映射St(x)進行n+1次計算:St(x)，St(x+Δe1)，···，St(x+Δen)，并代入(11)式得到近似Jacobi 矩陣Ut(x) .新算法是將上述Jacobi 矩陣的估算方法與經典Lyapunov 指數算法[8]相結合，其中的所有其他步驟都與經典Lyapunov 指數算法相同，主要區別在于Jacobi 矩陣是從近似公式(11)而不是(4)式獲得.令tj ∈R+，j0，1，···，J為1個遞增的時間序列，xjx(tj) .假設初始條件t00并且x0x(t0)x0，則 Δtjtj -tj-1和x(j-1)代入(11)式中就可以得到矩陣(x(j-1)) 的近似值.這種方法的最大優點是，不再要求軌跡上每個點的向量場f必須連續.應用(11)式時，只要滿足對于每個tj，軌跡(x) 在點x(j-1)處對于所有狀態變量是可微的，則系統中不論存在多少不連續性或不連續的類型均能滿足要求.同時，對時間序列tj僅要求tj ∈R+，j0，1，···，J是遞增的，tj值大小沒有限制.而且，不需要明確知道定義矢量場f的方程式，只要有一種計算軌跡(x) 的方法就足夠了.(x)的值無論是從軌跡(x) 的顯式定義或隱式定義，還是從數值過程，甚至是從實驗中獲得都沒有關系，該算法均有效.

以上提出的方法可以通過調整使其適用于離散時間不連續系統.與連續時間系統類似，離散時間系統的U(x) 可以理解為在點x處評估映射F的Jacobi 矩陣.可以表示為

因此，可以通過以下方式估算矩陣U(x) :

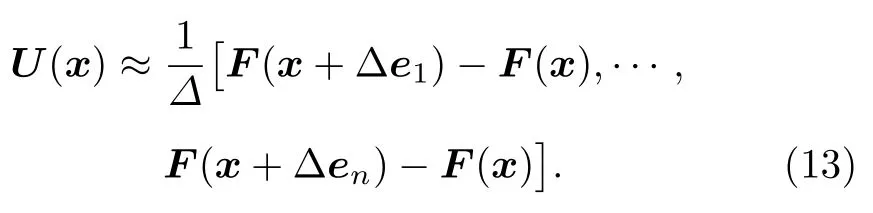
估算一次矩陣U(x)，需要對映射F進行n+1次計算:F(x)，F(x+Δe1)，···，F(x+Δen)，并代入(13)式得到近似Jacobi 矩陣U(x) .

基于以上分析，以連續時間不連續系統為例，不連續系統Lyapunov 指數算法如圖3 所示.

圖3 不連續系統Lyapunov 指數算法的示意圖Fig.3.Illustration of the algorithm of discontinuous system Lyapunov exponent.

不連續系統Lyapunov 指數算法實現的步驟如下.

2)使用初始條件x(j-1)在不連續系統中獲得新狀態x(j).

4)計算新的擾動:

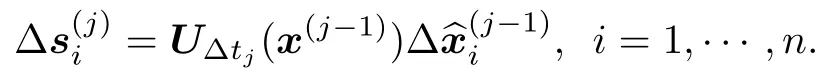
5)擾動正交化:

6)對于j1，2，···，T，重復以上2)—5)過程.然后，使用以下公式估算不連續系統的整個Lyapunov 指數譜:

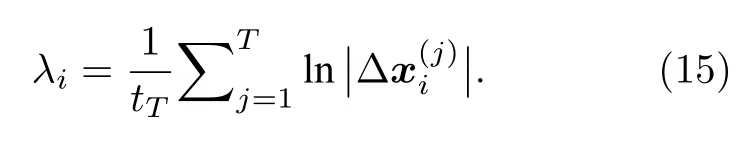
3 數值仿真研究

3.1 二自由度干摩擦沖擊振蕩器系統

二自由度干摩擦沖擊振蕩器系統由連接到剛度為k1的彈簧的質量塊M和阻尼系數為c1的黏滯阻尼器組成，另1 個質量塊m位于質量塊M上，其相對于M的位置由緩沖器A和B限制，質量塊之間存在摩擦力FT和阻尼系數為c2的黏性阻尼力.兩自由度沖擊振子是1 個質量-彈簧-阻尼系統，其中兩個質量塊可以相互碰撞，并在相對運動過程中存在干摩擦，如圖4 所示.

圖4 二自由度干摩擦沖擊振蕩器模型Fig.4.Model of the two-degrees-of-freedom (2-DoF) mechanical oscillator with impacts and friction.

二自由度沖擊振蕩器可由以下方程組描述:

其中M和m分別是外部和內部振動體的質量;x1，x2是它們的位置;k1是彈簧剛度;c1，c2是阻尼系數;FT是摩擦力;A是強迫振幅;Ω是諧波激勵的角頻率;δ0是內部質量塊m與外部質量塊M之間的間隙;μ是摩擦系數，R是恢復系數;tc是發生碰撞的時間.方程組(16)定義了振蕩器系統的演化，方程組(18)描述了在系統發生碰撞時刻tc處不連續性的狀態轉換.

將(16)—(18)式轉換為無量綱表示得到

在這個振蕩器系統中，沖擊和干摩擦的兩種不連續性都存在.假設對于任何初始條件y(0)，使得|y3-y1|＜y0，可以數值估計軌跡Sτ(y(0)) .唯一的限制是兩個物體在碰撞過程中的速度沒有定義.此外，還假設當 |y3(0)-y1(0)|＜y0和y2/y4時，軌跡Sτ(y(0))相對于初始條件是可微的.

3.2 數值仿真結果

為了將數值仿真結果與不同算法[35]獲得的結果進行比較驗證，控制參數η在[1.2，1.45]范圍內變化，并設定以下參數值:γ0.693，σ0.50，μ0.02，β0.05，y00.80，p1.00，R0.60，初始條件為零.采用自適應步長的龍格-庫塔(Runge-Kutta)方法對二自由度沖擊振蕩器系統進行了數值求解.在開始計算Lyapunov 指數和將軌跡點保存到分岔圖之前，每組參數針對運行該振蕩器系統，以減少瞬態影響.其中，Jacobi矩陣(x(j-1)) 通過(11)式獲得，為了保持方法的準確性，Δ值應與變分方程(4)的積分絕對誤差處于同一階或更低階，并考慮沖擊振蕩器系統中數據類型的近似誤差，從而確定Δ值取10—6.

由于最小擾動 Δy4的收縮速度過快，導致在計算自然對數時出現了數值問題.因此，僅給出了該振蕩器系統的3 個最大的Lyapunov 指數.為了觀察Lyapunov 指數值的穩定性，在估算程序的每次迭代之后，再利用(15)式計算結果.在每100 次迭代后，估計最后100 個λ1，λ2，λ3值的標準差.當所有標準偏差低于閾值10—4時，終止計算，并取最后100 次迭代中λ1，λ2，λ3的平均值作為最終值.圖5給出了3 個最大Lyapunov 指數圖和系統狀態分岔圖.可以觀察到，Lyapunov 指數值恰當地反映了系統在分岔圖中的行為.因此，通過新算法在二自由度干摩擦沖擊振蕩器系統(19)—(21)中的應用，證明了該Lyapunov 指數新算法的有效性.

圖5 二自由度干摩擦沖擊振蕩器系統的分叉圖和3 個最大Lyapunov 指數圖 (a) 狀態變量 y1;(b) 狀態變量 y2 ;(c) 狀態變量y3Fig.5.Bifurcation diagram and the corresponding diagram of the three largest Lyapunov exponents of the 2-DoF mechanical oscillator system with impacts and friction:(a) State variable y1;(b) state variable y2 ;(c) state variable y3 .

最后，對使用本文算法獲得的Lyapunov 指數計算結果與同步方法[35]得到的計算結果進行比較，可以得到，使用兩種算法獲得的最大Lyapunov 指數圖高度一致.從而，兩種方法也相互驗證了算法的正確性.

4 討論

在物理環境中，具有沖擊、干摩擦等因素的不連續系統，難以直接從變分方程中獲得Jacobi 矩陣，經典的Lyapunov 指數算法[8]變得難以實現，因此，本文算法基于攝動理論，在經典Lyapunov指數算法基礎上，采用差商近似導數獲得近似Jacobi 矩陣的方法，以損失一定Jacobi 矩陣計算精度為代價提升算法普適性.

本文算法應用于二自由度干摩擦沖擊振蕩器系統取得了較好的結果.計算得到了3 個Lyapunov指數譜圖和系統中3 個狀態變量的分叉圖，其中最大Lyapunov 指數也正確地反映了系統狀態變量在分叉圖中的軌跡變化，表明可以采用差商近似導數的方式獲得近似完備的Jacobi 矩陣，通過與連續系統經典Lyapunov 指數算法相結合，能夠有效地應用于包含沖擊、干摩擦等因素的不連續系統.在本算法中，差商近似導數法利用n+1 個不同初始條件向量:x0，x0+Δe1，···，x0+Δen在時間t上對系統積分求解Ut(x)，因此，求解Ut(x) 相當于求解n+1 階非線性系統的計算量.在經典算法中，通常變分方程(4)與系統軌跡St(x) 一起求解，可以將變分方程(4)視為n個線性時變系統，因此，求解Ut(x) 相當于求解1 個n階非線性系統和n個線性時變系統的計算量.只要系統狀態的時間導數值的計算量不比等式(4)中Ut(x) 后續列的時間導數的計算量大很多，則兩種算法的計算量是相當的.同時，許多非線性系統的矢量場f是通過狀態變量的和與積來定義的，都能夠滿足這個條件，例如著名的Duffing 或Lorenz 方程[11].差商近似導數法獲得近似Jacobi 矩陣中所需的每個軌跡St(x)，St(x+Δe1)，···，St(x+Δen)的積分是完全獨立的，每個軌跡都可以在使用單獨處理器的獨立進程中進行求解，使得新算法非常適合于多處理器計算模式，提升運算效率.

本文算法目前適應于對連續系統和不連續系統的Lypunov 指數譜進行提取，而實際應用中不連續系統的不連續性是多樣的，這就使得Lyapunov 指數的計算過程繁冗復雜.后續研究將圍繞如何繞過不連續系統的不連續點計算Lyapunov指數譜展開.

5 結論

本文基于經典Lyapunov 指數算法和攝動理論提出了一種計算不連續系統Lyapunov 指數的新算法，在經典Lyapunov 指數算法基礎上，利用相軌跡上的正交矢量型初始微擾動獲得近似Jacobi 矩陣.該算法不需要知道定義矢量場或者映射的方程式，只需要有一種獲得相軌跡的方法就足夠了，并且適用于連續或不連續的離散時間和連續時間系統.通過數值仿真分析，驗證了本文Lyapunov 指數算法簡單、有效和魯棒.本文提出的算法可以應用于包括不連續滑動振蕩器和許多其他不連續系統的大量不連續系統的研究.