基于大氣聲傳播理論的爆炸聲源能量估計

程巍 滕鵬曉 呂君 姬培鋒 戴翊靖

1) (中國科學院聲學研究所，中國科學院噪聲與振動重點實驗室，北京 100190)

2) (中國科學院大學，北京 100049)

提出了一種結合大氣聲場模擬與中近程超壓幅度衰減模型的爆炸聲源能量估計方法，針對傳統聲源能量估計公式未能充分利用大氣參數導致估計誤差過大的問題，本方法通過對大氣中傳播損失的數值模擬，大大提高了大氣參數對于聲源能量估計的修正效果，提高對聲源能量的估計精度.在地表化學爆炸實驗中，使用300—2500 km 距離的次聲接收信號，對比了傳統能量估計公式與基于大氣聲場模擬的能量估計方法對爆炸聲源的能量估計效果.實驗結果驗證了相對于傳統聲源能量估計方法，該方法降低聲源能量估計誤差的有效性.

1 引言

基于地面觀測信號對爆炸聲源參數進行估計是一種被動式遠距離信息感知手段，其中聲波探測是對聲源能量等信息進行估計的重要手段.地表附近爆炸產生的壓力波在大氣中衰減為聲波傳播，傳播過程中大氣對其各項吸收效應與其頻率呈負相關，而次聲波頻率較低(0—16 Hz)，在大氣中傳播衰減小，是對爆炸等事件遠距離監測的有效手段.全面禁止核試驗條約組織(CTBTO)為了監測全球核試驗狀況，建立了預期包含60 個次聲臺陣的國際監測系統(international monitoring system，IMS)，并將次聲作為爆炸源定位與能量估計的主要手段.現有的遠距離能量估計方法為來自于理論模型搭建與實驗測量數據相結合的半經驗公式.美國空軍技術應用中心(Air Force Technical Applications Center，AFTAC)根據理論模型與觀測數據提出比較適合低當量實驗結果的能量估計半經驗公式，使用參數為聲壓峰值和距離[1].1995 年洛斯·阿拉莫斯國家實驗室(Los Alamos National Laboratory，LANL)根據聲波在大氣中衰減特性與多次爆炸實驗的數據總結，總結出普適性更佳，包含聲壓峰值、距離與大氣風速參數的能量估計半經驗公式[2].俄羅斯巖石動力學研究所(The Institute for the Dynamics of the Geospheres，IDG)根據傳播方向與風向的垂直關系分別進行修正，對聲源能量進行估計[3].2002 年，Kulichkov 根據脈沖信號N 形波動量保持理論，利用遠距離接收的N 形波與U 形波的沖量對聲源能量進行估計[4].

由于大氣參數呈層狀分布，溫度與水平風速隨海拔的變化使得次聲在大氣中以波導形式傳播.大氣參數的垂直參數分布決定聲波在大氣中不同傳播方向的波導模式.在LANL 提出的聲源能量估計公式中，使用平流層頂水平風速作為大氣參數修正因子，該公式由于計算速度快、誤差相對較小而被廣泛使用，但其修正因子對于大氣參數的利用率很低，這導致其修正范圍有限且穩健性很差.本文從大氣聲傳播理論出發提出一種使用大氣全高度垂直參數修正的聲源能量估計方法，通過大氣中計算聲學方法對接收聲壓幅值進行修正，并針對聲源中近距離范圍提出適用的超壓幅值衰減模型，大大提高了使用遠距離接收次聲信號幅值對聲源能量估計的準確性.

2 大氣全高度垂直參數修正的能量估計方法

2.1 問題提出

LANL 研究了美國內華達試驗場附近觀測站點全年接收聲壓信號隨日期的變化，觀察到位于聲源東側的次聲臺陣接收聲壓值在夏季顯著減小，而位于南北方向次聲臺陣接收聲壓值全年幾乎不變.通過研究水平風速隨季節的變化，研究人員認為夏季風向與聲波傳播方向相反導致接收聲壓的異常減小，因此使用平流層頂水平風速用于修正接收點的聲壓:

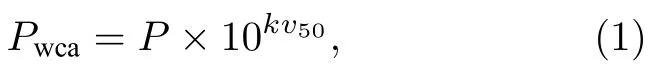
其中v50為海拔50 km 處水平風速在水平聲波傳播方向的分量，k=0.019 為一階修正系數，P為接收聲壓幅度，Pwca為風速修正后的聲壓.對于聲波遠距離傳播，研究人員采用R/W0.5作為比例距離對大量化學爆炸測試數據進行回歸分析，其中R為傳播的距離，單位為km;W為聲源能量，單位為kt.通過最小二乘法得到聲源能量估計公式:

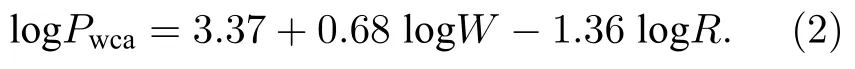
(2)式使用50 km 海拔處風速以簡化運算.當風速為正值時，平流層頂部的有效聲速極大值大于地面聲速，產生平流層波導[5]，這使得接收點聲壓幅度偏大;當風速為負值時，則次聲在大氣中的傳播只存在熱層波導，由于熱層中聲波傳播的經典衰減與轉動衰減[6]帶來的衰減量非常明顯，這使得接收點的聲壓幅度偏小.在平流層頂未出現異常擾動時，(2)式可以對聲源能量進行較為準確的估計.但在實際使用中，使用單一參數v50作為大氣修正因子導致聲源能量估計值誤差較大，而計算大氣聲學綜合大氣溫度、風速和黏滯系數等因素的影響，可降低對聲源能量估計的誤差.

常用的計算大氣聲學方法有射線法、拋物方程法、非線性漸進波動方程法(nonlinear progressive wave equation，NPE)和有限元方法[7，8].射線法使用的聲線模型無法讀取出任意位置點的能量值，首先予以排除.由于本方法需要獲取觀測點位置聲波能量損失值，應盡量多考慮大氣中的影響因素，而有限元方法在遠距離仿真狀況下計算量過大，缺乏實際可用性，因此選用相對于拋物方程法額外考慮到折射效應與非線性陡峭等非線性效應的NPE 數值模擬方法.

2.2 非線性漸進波動方程

聲波在大氣中的傳播受大氣流體特性的影響，將聲壓方程組中的運動方程添加介質黏度項，并將物態方程中的聲壓展開至二階[9]:

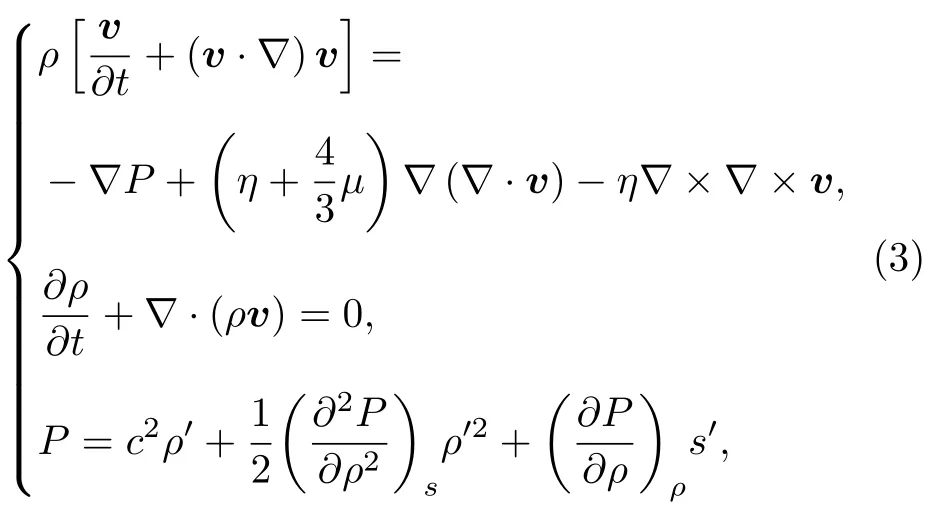
其中P為聲壓，ρ為大氣密度，s為熱力學中的熵，η為體積黏度，μ為剪切黏度.相對于拋物方程等方法，NPE 通過對絕熱方程的展開保留二階項以考慮聲波在大氣中傳播的非線性效應.將

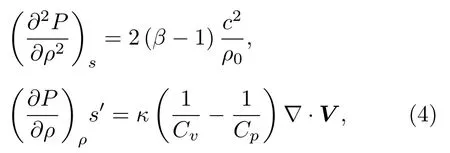
代入方程組(3)中的物態方程，得到方程

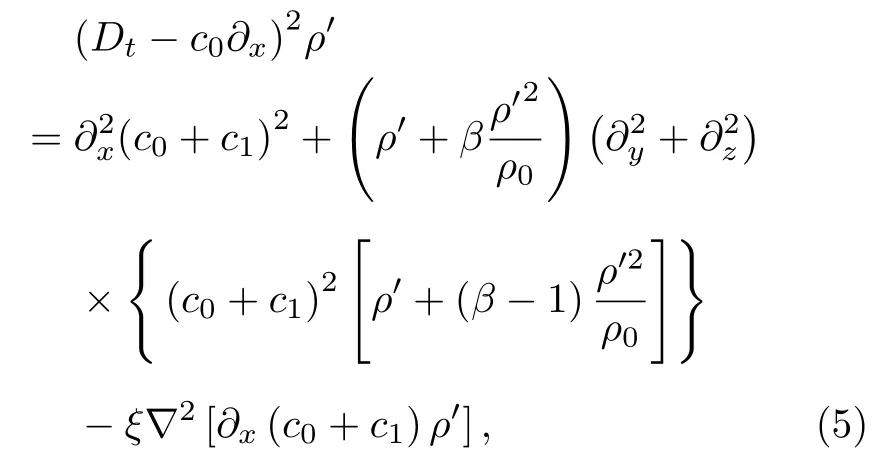
其中熱黏滯系數ξ為

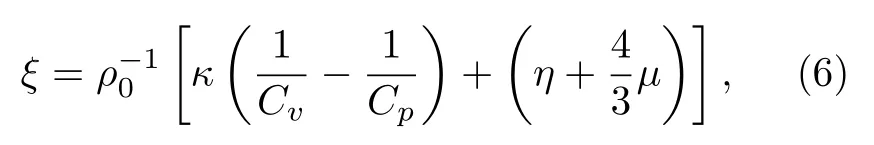
其中κ為熱傳導系數，Cv為定容比熱，Cp為定壓比熱.熱黏滯項的計算主要估計了聲波在大氣中傳播的經典衰減.

將方程(5)展開后，忽略高階小量后可化簡得到NPE 在笛卡爾坐標下的標準形式:

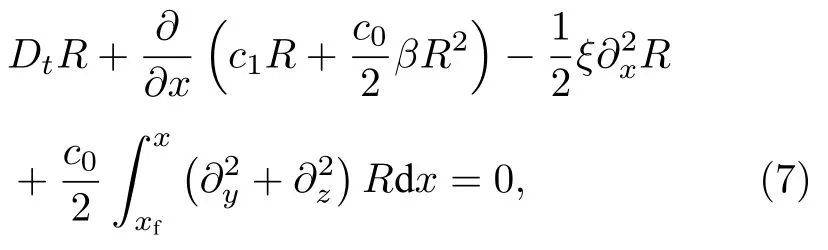
其中Dt?t+c0?x為運動框算子，使得計算域隨著聲波傳播而運動，Rρ′/ρ0為歸一化密度擾動，c0為靜態大氣中聲速，c1為隨運動計算框變換的聲速擾動，β為非線性系數，ξ為熱黏滯系數.實際處理中，考慮到大氣各項參數呈層狀分布，通常使用圓柱坐標系進行數值模擬[10]:

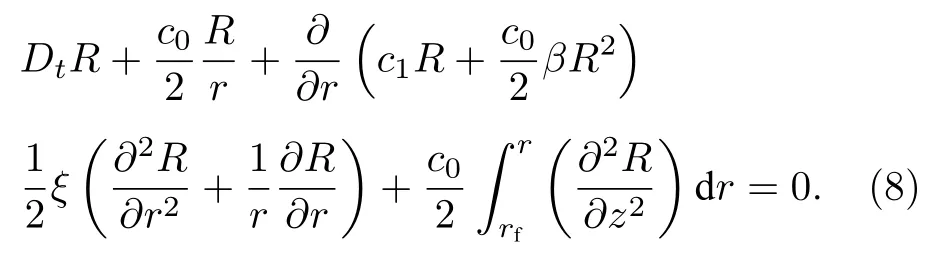
使用算子分裂法[11]將(4)式分解為4 個步驟，并分別使用不同格式進行數值求解，其中

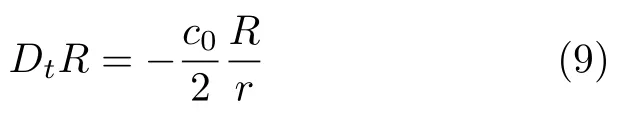
為圓柱擴散效應項，使用Crank-Nicolson 差分格式進行數值計算;

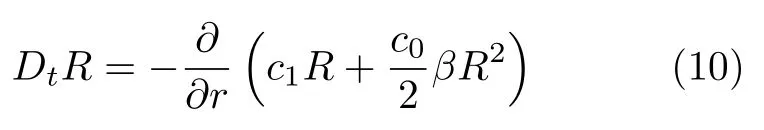
為折射與非線性效應項，將此兩項結合使用通量校正法[12]進行數值計算可以提高計算效率;

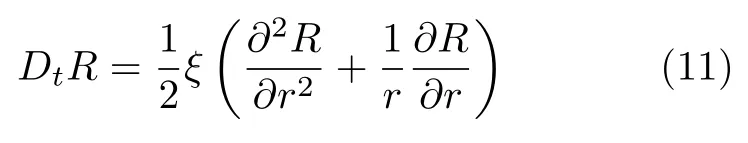
為熱黏滯吸收效應項，

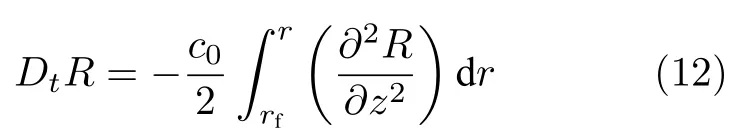
為衍射效應項，均使用Crank-Nicolson 差分格式與Thomas 算法結合求解.設定地面為剛性邊界條件，使用完美匹配層[13]設定大氣上邊界為吸收邊界條件，通過運動框滑動疊加計算出聲源在設定傳播方向的傳播損失分布.

由于NPE 算法中使用的傳播損失量由運動窗疊加求得，則傳播損失的絕對數值與運動框步長負相關，無法直接用于聲源能量估計，因此需要使用傳播損失的相對數值通過間接法進行計算.根據本節前文的描述，NPE 方程對非強非線性線性聲波傳播范圍內可進行有效的模擬，對于更近范圍內的聲波能量傳播損失值的模擬，由于未能保留更加高階的小量[14]，無法對此范圍內沖擊波的強非線性效應進行準確模擬.因此，如果直接使用接收臺陣位置的傳播損失量作為對聲源能量估計，聲源附近的強非線性效應模擬誤差與輸入聲源函數特性的影響為能量估計帶來額外的誤差，因此本文采用弱非線性效應區域傳播損失相對值法進行聲源能量估計.

假設次聲臺陣距離聲源距離為rt，通過NPE方程求得臺陣位置傳播損失量為PLrt，接收到聲壓單峰幅值為prt.設定距離聲源r0為參考距離，此位置傳播損失量為PLr0.在爆炸產生的沖擊波研究中通常使用的參數為比例距離Z，其中r為水平距離，單位為m;W為聲源能量，單位為kg[15].當與聲源距離滿足Z＜20m/時，該范圍為近場區域.在此區域內爆炸聲源產生的高溫、高壓燃爆物急劇膨脹，將附近空氣迅速排擠形成壓縮空氣層.此壓縮空氣層以超音速運動且其狀態參數有突躍，稱為沖擊波，其前沿稱為波陣面.在近場區域時，沖擊波超壓幅度滿足的方程滿足強非線性條件.隨著傳播距離的增加，波陣面上的壓強等參數快速下降，接近衰減為聲波時滿足弱非線性條件.由于本方法使用NPE 作為數值模擬方法，則參考距離應超出強非線性影響范圍，即[16].將r處聲壓轉化為r0處超壓幅值Pr0的轉移方程為

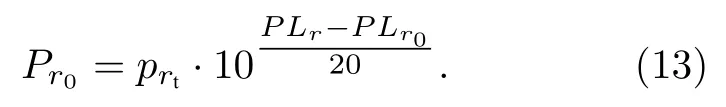
使用通過轉移方程(13)計算得到的參考超壓幅值對聲源能量進行進一步估計.

2.3 中近程超壓幅度衰減模型

使用2.2 節計算得到的參考聲壓，可根據以下超壓幅度衰減模型對聲源能量進行估計[15，17，18]:

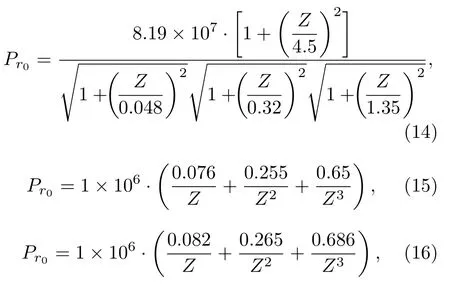
其中Pr0為r0處超壓幅值.上述超壓值隨比例距離變化的公式主要適用于比例距離較小的狀況，根據2016 年Kim 和Rodgers[14]適用的實驗測量，(14)—(16)式在范圍內與實測數據符合狀況很好，但在范圍內，預測值與實際測量結果偏差很大.為了驗證此類聲源能量估計公式對于不同比例距離的適用狀況，本文使用Humming Roadrunner (HRR)實驗數據與美國1951—1958 年在內華達試驗場(Nevada test site，NTS)附近各臺陣測得的直達波信號幅度數據對其進行評估測試[19]，對比結果見圖1.根據對比結果，在范圍內，傳統超壓幅值衰減模型與實際測量信號符合狀況較好，反映出沖擊波超壓幅值隨比例距離增加的快速衰減過程;但是在范圍，實際觀測到的信號隨距離衰減速度明顯快于傳統衰減模型.在此范圍內，傳統超壓幅度衰減與1/Z近似呈線性相關，觀測信號超壓幅度亦呈線性相關，但其系數取值差異很大.

本文提出的方法中，參考距離r0應位于Z ＞范圍以減少數值模擬帶來的誤差，因此需要針對此比例距離范圍，根據實測數據提出合理的超壓幅度隨比例距離衰減的經驗公式.通過最小二乘法在對數坐標系下對實測數據進行線性擬合，得到適用于本方法的中近程超壓幅度衰減模型(middle range model，MR):

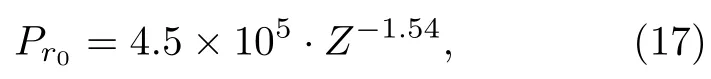
化簡為聲源能量估計方程為

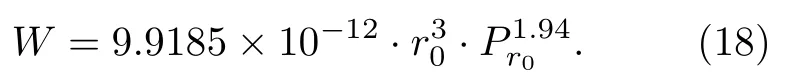
從圖1 中的NTS 觀測數據可以看出，隨著比例距離Z的增加，對于超壓幅值預測值的方差逐漸增加，為了獲得更高的聲源能量估計精度，r0取值應盡量使得對應Z0取值接近 50m/.但在實際使用過程中，本文使用NPE 方程進行數值模擬時在水平方向的步進為100 m，而NPE 方法對于初始聲源函數附近模擬值收斂速度較慢產生計算誤差，當r0取值過小時會導致聲源能量估計錯誤.根據多次實驗結果，r0應大于50 倍NPE 中水平方向步進，即r0＞5 km，綜合Z0＞50 m/的限制條件，本方法僅適用于聲源能量W ＜1 kt 的狀況.圖1 給出了(14)—(16)式分別對應的超壓幅值衰減模型與本文提出的衰減模型效果對比，其中KG85 模型為Kinney 與Graham 于1985 提出的化學爆炸超壓衰減模型[15];Sadovskyi 模型為根據模型相似律建立的公式，由實驗測量確定系數，得到高爆炸藥沖擊波峰值超壓的變化模型，使用范圍為比例距離Z滿足1 ＜Z＜ 15[17];王儒策模型為根據原子爆炸的經驗，球形裝藥在無限空氣介質中爆炸時的超壓變化規律[18].

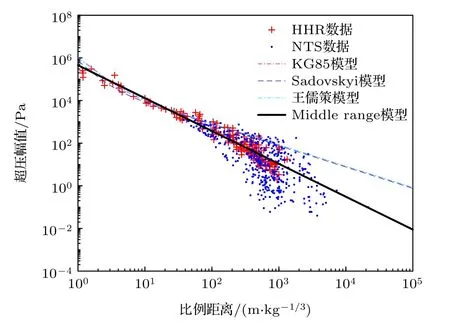
圖1 各衰減模型與實測數據對比Fig.1.Comparison of each attenuation model with measured data.

3 實驗與討論

為了驗證本計算方法的普適性，使用2011 年1 月24 日在以色列Sayarim 進行的化學爆炸實驗數據[20]進行驗證，聲源位置坐標為34.81668°E，29.99555°N，實驗測量得到的數據與相關參數見表1，其中的風速數據來自HWM14 大氣風場模型.實驗聲源為在地表進行的化學爆炸，其能量為7.4 噸TNT.由于并未獲得該數據的波形數據，Kulichkov[4]提出的基于脈沖聲沖量保持理論的計算方法無法使用，故本文將使用LANL 提出的普適性能量估計公式進行對比計算，其顯式聲源能量估計形式為

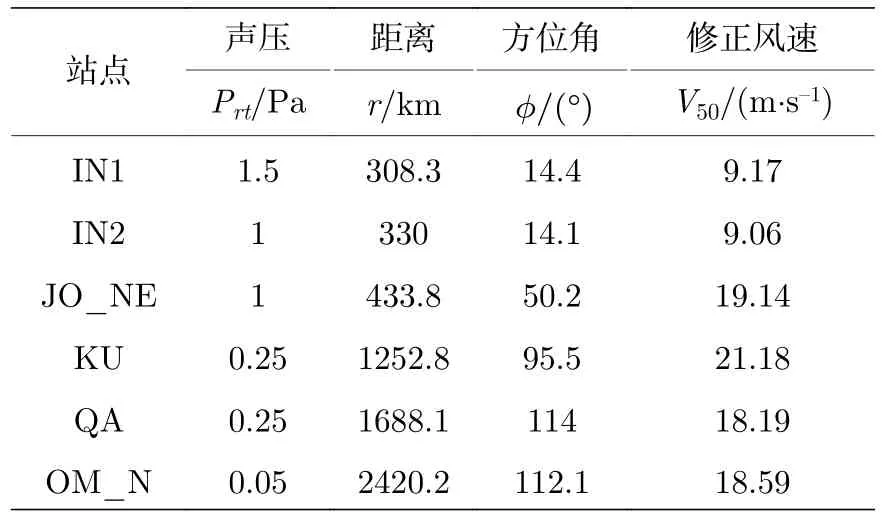
表1 2011 年Sayarim 實驗各接收點數據與參數Table 1. Parameters of each array in Sayarim experiment in 2011.

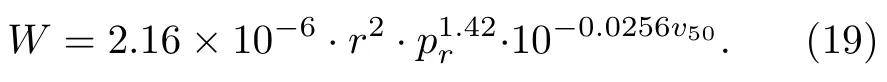
而在使用本文提出的基于大氣傳播模擬的聲源能量估計方法時，采用r07 km 作為參考距離，以HWM14 與MSISE00 模型作為大氣參數剖面模型，得出如圖2 的聲源向各臺陣方向的傳播損失分布圖.

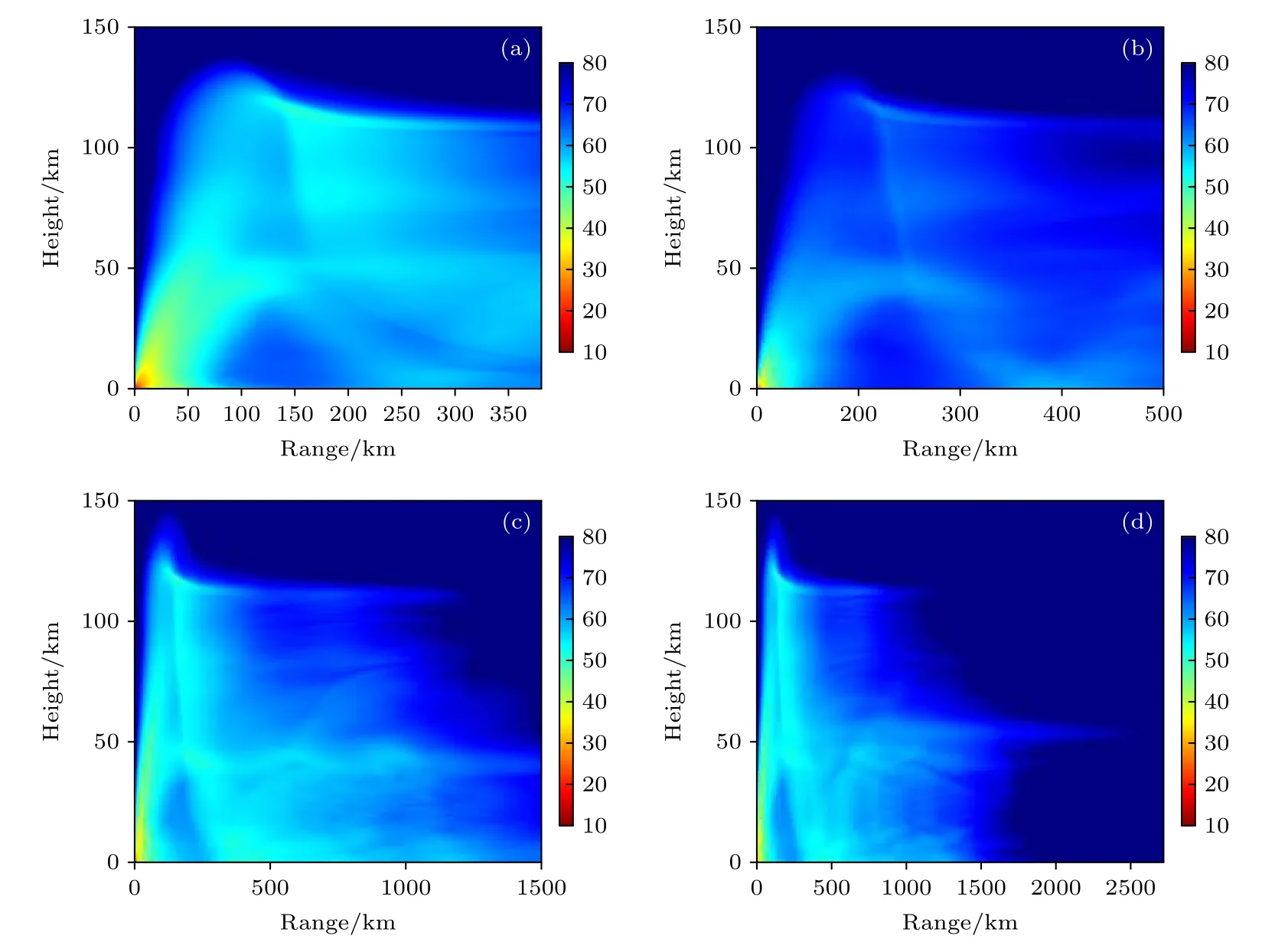
圖2 4 個主要傳播方向的NPE 傳播模擬結果 (a)方位角14°方向的傳播損失分布;(b)方位角50°方向的傳播損失分布;(c)方位角95.5°方向的傳播損失分布;(d)方位角113°方向的傳播損失分布Fig.2.NPE propagation simulations in four main propagation directions:(a) Propagation loss distribution in the azimuth of 14°;(b) propagation loss distribution in the azimuth of 50°;(c) propagation loss distribution in the azimuth of 95.5°;(d) distribution of propagation loss in the azimuth of 113°.

為了驗證參考距離的選取對聲源估計精度的影響，選取r01，2，3，···，30 km 進行對比計算，誤差對比見圖3.圖中的變化曲線表明，隨著參考距離的減小，除JO_NE 和KU 點位數據的計算結果外，對聲源能量的估計誤差逐漸減小，并在參考距離5—10 km 之間達到最小誤差.對于JO_NE 和KU 點位數據，由于參考聲壓系統性偏小，因此計算得到的聲源能量估計值的誤差隨著參考距離的減小逐漸增加.

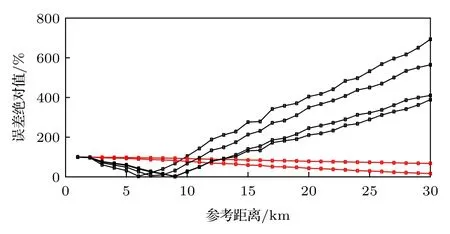
圖3 估計誤差隨參考距離選取變化圖Fig.3.Error changes with reference distances.

選取參考距離分別為7 與20 km 進行聲源能量估計數值的具體對比，結果見表2，表中r07 km下聲源能量估計結果的誤差遠小于r020 km下的誤差，對應比例距離分別為Z0359 m/和Z01026 m/，此誤差變化結果與圖1 中方差變化趨勢一致.對于JO_NE 臺陣與KU 臺陣的數值模擬結果，其中JO_NE 在433 km 附近傳播損失很小，此項模擬偏小導致參考聲壓的計算值偏小，影響計算結果;KU 臺陣在此距離傳播損失很小，此項偏小導致參考聲壓的計算值偏小，導致計算結果整體偏小.使用不同的格點長度計算后，模擬的結果近似，表明該誤差并非由格點精度導致.

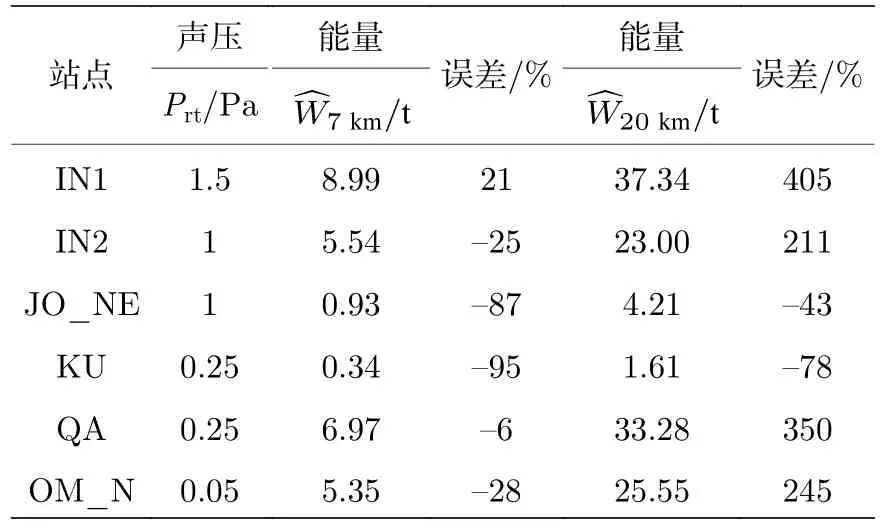
表2 參考距離為7，20 km 時聲源能量估計結果對比Table 2. Comparison between sound source energy estimation results at reference distance of 7，20 km.

根據圖2 中的數值計算結果，在方位角為14°，50°，95.5°和113°這4 個方向的次聲傳播過程中均存在平流層波導.與此一致的是，在表1 中這6 個點位對應的v50均為正值，即認為存在平流層波導，LANL 公式對聲源能量估計值修正減小.對該數據分別使用LANL 提出的能量估計公式和本文提出的NPE_MR 方法對聲源能量進行估計，估計結果與誤差的對比結果見表3.

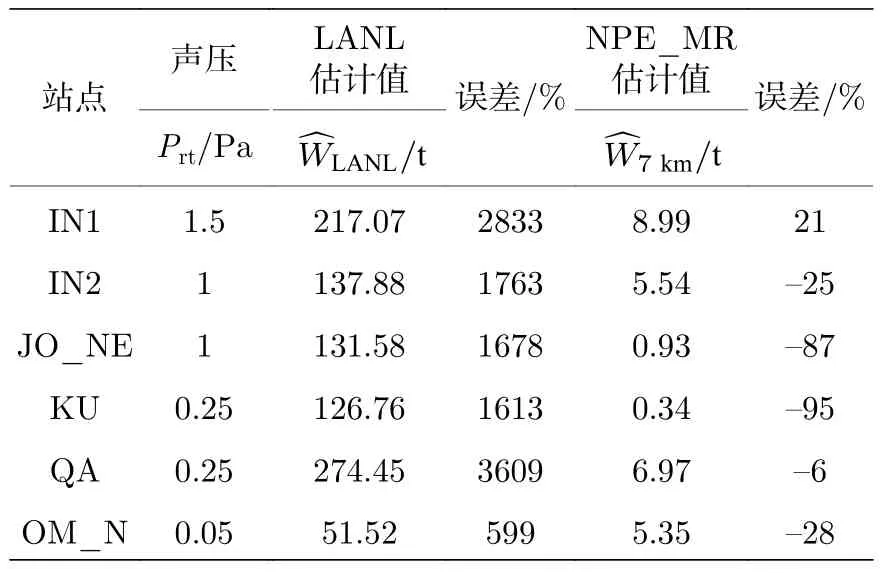
表3 2011 年Sayarim 實驗聲源能量估計結果對比Table 3. Comparison between sound source energy estimation results in Sayarim experiment in 2011.

表3 中的6 個觀測點位分布在距離聲源300—2500 km 之間的范圍內，通過表內誤差的對比可以觀察到，對于此次化學爆炸試驗，LANL 聲源聲量估計公式對聲源能量的估計明顯偏大.表1 中的v50數值表明該公式對聲源能量的初始估計值的修正方向正確，但是由于大氣中該高度處的風速幅值有限，對于此數據對應的狀況無法進行正確的修正.而本文提出的NPE_MR 聲源能量估計方法充分利用了聲波傳播過程中的大氣剖面參數，對于各接收點的信號幅度進行了合適的修正，大大降低了對爆炸聲源的能量估計誤差.

在實際使用中，次聲信號可以被相對于聲源位置不同方位角的多個次聲臺陣接收到，而LANL提出的聲源能量估計公式在計算比較快速的情況下，對于聲源能量的估計誤差一般在300%以內，可直接使用多陣平均值對聲源能量進行估計.但是對于大氣參數對接收信號影響較大的情況下，傳統聲源能量估計方法的估計誤差可能達到將近4000%，在多陣計算中只能作為錯誤項去除.而通過本文提出的NPE_MR 聲源能量估計方法，可以將大氣參數對接收聲波幅度的影響進行大幅度修正，得到可用于多陣平均計算的結果，提高接收陣的信息利用效率，減小對聲源能量估計的誤差.

4 結論

對于通過大氣遠距離傳播的次聲信號，美國與俄羅斯使用大氣中的風場信息對其進行修正以減小聲源能量估計的誤差.其中美國LANL 提出的包含風速修正項的聲源能量估計公式對聲源能量的計算誤差最小，但是在傳播損失特別大時，由于修正項可提供的修正幅度有限，無法將估計值誤差修至300%以下.本文提出了利用大氣中傳播模擬仿真與MR 衰減模型的聲源能量估計方法，大大拓寬了大氣參數對于聲源能量估計值的修正范圍.在實驗驗證中，本文使用2011 年以色列Sayarim化學爆炸實驗的實測數據，對比了本方法與傳統半經驗計算公式計算結果之間的誤差，證明本方法在需要使用大氣數據對初始聲源能量估計結果進行大幅度修正的情況下比傳統半經驗公式有更好的性能.在后續的工作中，需要對NPE 方法的穩定性做進一步的提高，減少聲源能量估計值異常偏小的情況.