大密度比氣泡在含非對稱障礙物微通道內(nèi)的運動行為*

賀傳暉 劉高潔 婁欽

(上海理工大學能源與動力工程學院，上海 200093)

采用格子玻爾茲曼方法研究了含非對稱障礙物微通道內(nèi)氣泡變形、分裂、上升速度、以及剩余質(zhì)量比的變化規(guī)律.研究結(jié)果表明，首先，氣泡在穿過通道的過程中變形加劇時其上升速度會減小.其次，隨著E?tv?s 數(shù)增加，氣泡在穿過障礙物的過程中形變越來越嚴重，速度越來越大且通過時間越來越小.除此之外，隨著氣液黏度比增加，氣泡變形更嚴重，上升速度顯著增加，且氣泡剩余質(zhì)量比減少.另一方面，隨著障礙物縱向距離增加，氣泡通過障礙物的時間減少，而氣泡的剩余質(zhì)量比呈現(xiàn)近似不變-增加-減小-增加的變化趨勢.再者，為了研究障礙物橫向距離對氣泡運動形態(tài)的影響，考慮了兩種情況:一是兩障礙物長度同時改變;二是僅改變單側(cè)障礙物長度.結(jié)果表明，對于以上兩種情況，當橫向距離較小時，僅改變單側(cè)障礙物長度造成氣泡通過障礙物的時間更長.最后，研究結(jié)果還表明當右側(cè)障礙物寬度足夠大時，氣泡離開障礙物時的位置幾乎不變，而隨著右側(cè)障礙物寬度的增加，氣泡穿過障礙物的時間緩慢增加，氣泡的剩余質(zhì)量比先近似不變?nèi)缓蟠蠓陆底詈笥直３纸撇蛔?

1 引言

自然界和工業(yè)過程中廣泛存在著與氣泡有關的現(xiàn)象，例如日常生活中的沸騰現(xiàn)象，肥皂泡在空氣中的上升和破碎現(xiàn)象等.在工業(yè)生產(chǎn)中，燃料電池、冶金行業(yè)、核事故防泄漏處理、注氣開采油藏等也都和氣泡息息相關[1-7].例如，燃料電池中二氧化碳氣泡的生成、脫離和輸運規(guī)律直接影響其使用時間和性能[8，9];冶金反應器中氣泡的產(chǎn)生、聚并以及破碎過程對其反應速率有重要影響[10];超聲波采油技術(shù)[11]中微氣泡的膨脹和破裂決定了原油的產(chǎn)量.因此微通道中氣泡的行為研究對自然界現(xiàn)象的解釋以及工業(yè)生產(chǎn)過程中的優(yōu)化具有十分重要的意義.

目前，已有學者通過理論分析、實驗研究或者數(shù)值模擬的方法對氣泡的運動行為開展了大量研究工作，Davies 和Taylor[12]通過理論和實驗方法研究了體積較大的氣泡在空氣中上升時的形狀變化以及上升速率，建立了氣泡上升速度和曲率之間的關系式.Walters 和Davidson[13]進一步采用理論和實驗方法研究了氣泡上升過程中的形狀變化規(guī)律，發(fā)現(xiàn)氣泡最初的形狀變化主要與浮力和黏度有關.Unverdi 和Tryggvason[14]采用鋒面跟蹤法研究了三維黏性不可壓縮多相流中氣泡的上升過程.艾旭鵬和倪寶玉[15]利用氣泡邊界層理論研究了黏性流體下的氣泡運動，他們指出比較大的流體黏性會降低氣泡射流速度.Rabha 和Buwa[16]基于流體體積(Volume of Fluid，VOF)方法調(diào)查了線性剪切作用下不同性質(zhì)的液體中單個及多個氣泡的上升行為，并研究了相鄰氣泡之間的升力作用.同樣采用流體體積方法，Moran 等[17]探究了在水平管道中運動的一個拉長氣泡的運動形態(tài)，主要研究了不同毛細數(shù)、邦德數(shù)以及雷諾數(shù)時氣泡形狀的變化.Chakraborty 等[18]將VOF 和Level Set 方法進行耦合，討論了在低雷諾數(shù)大黏度比下的氣泡在垂直管內(nèi)的運動過程.

以上不同方法對氣泡運動形態(tài)的研究工作揭示了影響氣泡變化的因素，為人們認識氣泡在通道內(nèi)的運動規(guī)律提供了理論基礎.另一方面，在對微通道氣泡行為進行數(shù)值研究時，格子玻爾茲曼(lattice Boltzmann，LB)方法憑借其簡單的相界面處理方法及易于實現(xiàn)邊界條件等優(yōu)點被研究人員廣泛應用于兩相流問題的研究.采用LB 方法，Anwar[19]研究了不同E?tv?s 數(shù)(Eo)、Morton 數(shù)(Mo)、Reynolds 數(shù)(Re)下氣泡的終端速度和形狀.結(jié)果表明，隨著黏度比的降低，氣泡終端的形變程度越小、末端速度越低.Alizadeh 等[20]研究了氣泡通過圓管之后的形狀變化，發(fā)現(xiàn)改變管之間的距離及其相應的直徑會導致氣泡的形狀不同.婁欽等研究了含對稱半圓形微通道內(nèi)[21]以及分叉微通道內(nèi)[22]氣泡的動力學行為.Yi 和Xing[23]調(diào)查了煤層中煤的潤濕性對氣泡行為的影響，研究結(jié)果表明，氣泡的大小和接觸角對氣泡和水的流動能力都有顯著影響.Sattari 等[24]研究了多孔介質(zhì)中不同Eo數(shù)和壁面潤濕性時氣泡的行為，他們觀察到了氣泡的分裂現(xiàn)象，并發(fā)現(xiàn)在中等Eo數(shù)時氣泡能夠不受干擾地通過障礙物，而低Eo數(shù)則容易出現(xiàn)蒸汽覆蓋現(xiàn)象.Yu 等[25]研究了不同Re數(shù)和Eo數(shù)時充滿圓形及半圓形障礙物的微通道內(nèi)氣泡變形、破碎、合并、阻力系數(shù)以及穩(wěn)態(tài)流型.

上述工作研究了氣泡的運動機理，從多方面調(diào)查了氣泡在微通道內(nèi)的運動行為，并對氣泡穿過障礙物時產(chǎn)生的分裂現(xiàn)象、運動軌跡等進行了闡述.但現(xiàn)有的研究大多數(shù)是在較小密度比下進行的，很少考慮氣液間大密度比的情況，而實際上大密度比氣泡廣泛存在于工業(yè)過程中，是一個無法忽視的研究問題.其次，對于微通道中障礙物的設定，已有研究較一致地將障礙物對稱分布，較少研究障礙物的非對稱性對氣泡運動行為的影響，但工業(yè)上氣泡在逃逸過程中所碰到的管壁上的障礙物通常是隨機的.因此，本文研究大密度比氣泡在含非對稱性障礙物微通道內(nèi)微觀界面動力學行為以及宏觀運動現(xiàn)象，主要研究氣泡不同表面張力、黏度比、障礙物大小、障礙物位置對氣泡上升過程中形態(tài)變化、剩余質(zhì)量比、上升速度、以及通過通道時間的影響.

2 格子玻爾茲曼模型

Liang 等[26]提出的相場LB 方法在研究大密度比兩相流問題時穩(wěn)定性較好[27]，因此本文采用該模型研究大密度比氣泡在含非對稱障礙物微通道內(nèi)的運動行為.該模型的界面演化函數(shù)fi(x，t)用于求解Allen-Cahn 方程[28，29]，其形式如下:

而它的流場演化函數(shù)gi(x，t) 用于求解Navier-Stokes 方程[30，31]，其形式如下:

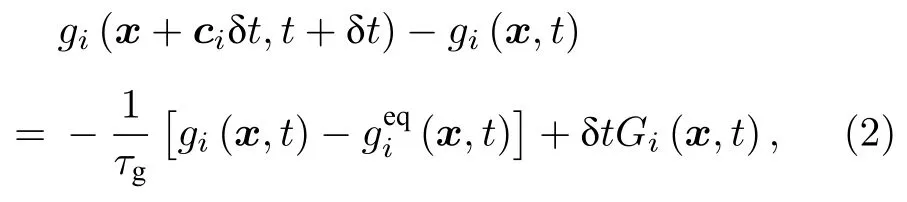
其中τf，τg分別為界面演化函數(shù)和流場演化函數(shù)對應的無量綱弛豫時間，F(xiàn)i(x，t)是源項，Gi(x，t) 是力項.(x，t) 和(x，t) 分別為界面演化函數(shù)和流場演化函數(shù)對應的平衡態(tài)分布函數(shù)，它們可以分別表示為

其中

Φ，ρ，u分別代表相場指標函數(shù)、流體密度和流體速度;cs是聲速;ci是離散速度;ωi是加權(quán)系數(shù).ci和ωi取決于所使用的離散速度模型.在本文中采用D2Q9 格子模型，該模型對應的加權(quán)系數(shù)ωi分別為ω04/9，ω1-41/9，ω5-81/36，對應的離散速度配置如下:

其中cδx/δt是晶格 速度，δx和δt分別表示空間步長和時間步長，而cs為模型常數(shù)，在本文中將 δx和 δt設置為長度和時間單位，即 δxδt1 .方程(1)中的Fi的形式如下:

方程(2)中Gi的表示如下:

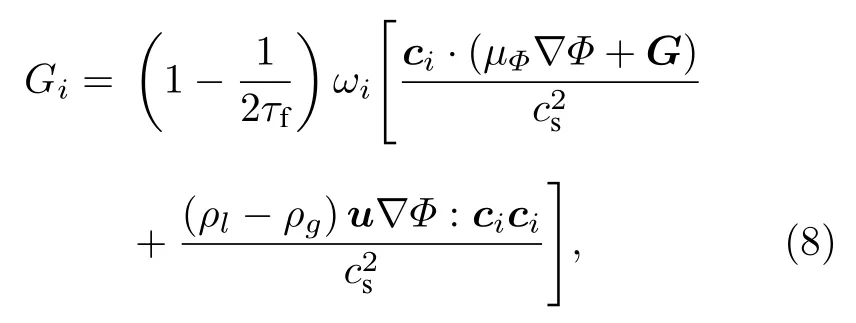
式中μΦ為化學勢，定義為

其中k和β為模型參數(shù)，它們與界面厚度W和表面張力σ的關系為

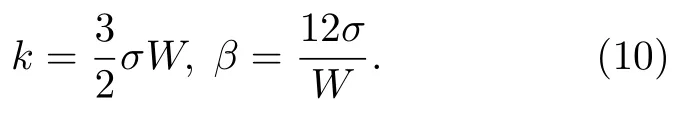
根據(jù)Chapman-Enskog 分析可以得到流場的宏觀量如下[26，32]:

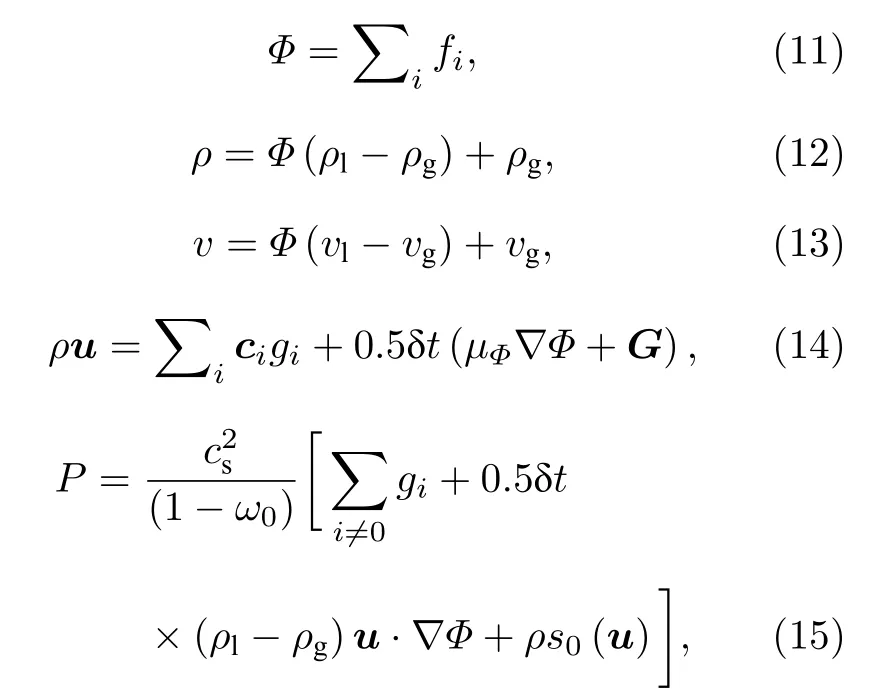
其中ρl和ρg分別代表液相和氣相的飽和密度，vl和vg代表液相和氣相的運動黏度.需要指出的是流體的松弛時間τg和運動黏度v有如下關系:

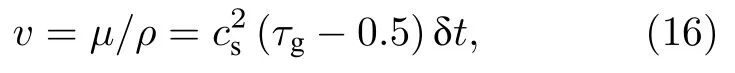
其中μ為流體的動力黏度.而松弛時間τf與遷移率M的關系如下:

梯度項通過二階中心各向同性方法計算[33]:

3 模型驗證

采用Laplace 定律對程序的正確性進行驗證.數(shù)值模擬中，在長度和寬度均為128個網(wǎng)格的方形計算區(qū)域中心放置一個半徑為R，密度為ρg1，黏度μg1.0 的氣泡，該方形計算區(qū)域的其他部分是密度ρl1000，黏度μl100 的液體，計算區(qū)域的四周均為周期性邊界條件.其他參數(shù)設置如下:M0.1，σ0.312，Φl1，Φg0，R20，W4，g0.松弛時間τf和τg可由給定的遷移率以及流體黏度得到(根據(jù)(16)式和(17)式).根據(jù)Laplace定律，對于該問題，當系統(tǒng)達到穩(wěn)定時，氣泡內(nèi)外壓力差滿足Laplace 定律[21，34]:

為了驗證Laplace 定律，在數(shù)值模擬中分別取了五種不同的半徑情況，即R24，28， 32， 36，40，取三種不同表面張力，即σ0.2， 0.15，0.1 .對于以上所有情況，當計算達到穩(wěn)定后，得到的氣泡內(nèi)外壓力差Pi-Po與半徑之間的關系如圖1 所示.可以看出，計算結(jié)果符合Laplace 定律.

圖1 Laplace 定律驗證Fig.1.Laplace law verification.

4 物理問題描述

本文研究的物理問題如圖2 所示，在寬為W0、長為L0的通道左右壁面上設置兩個非對稱障礙物，其中左側(cè)障礙物的長度和寬度分別為Ll和Wl，右側(cè)障礙物的長度和寬度分別為Lr和Wr，兩障礙物底邊與管道左右壁面的交點分別為 (0，yl) 和 (0，yr)，初始時在管道內(nèi)放置一個密度為ρg，半徑為R，圓心為(xc，yc) 的氣泡.而管道的其他部分充滿密度為ρl的液體，在y方向施加力G，則氣泡在流體區(qū)域內(nèi)向上運動.計算區(qū)域的上下邊界條件為周期邊界，左右壁面及障礙物表面采用Ladd[35，36]提出的無滑移半反彈邊界條件，本文未考慮壁面潤濕性的影響，關于壁面潤濕性對氣泡運動行為的影響我們會在后續(xù)工作中進行系統(tǒng)研究.該物理問題有一個重要無量綱數(shù)，即E?tv?s 數(shù)(Eo):

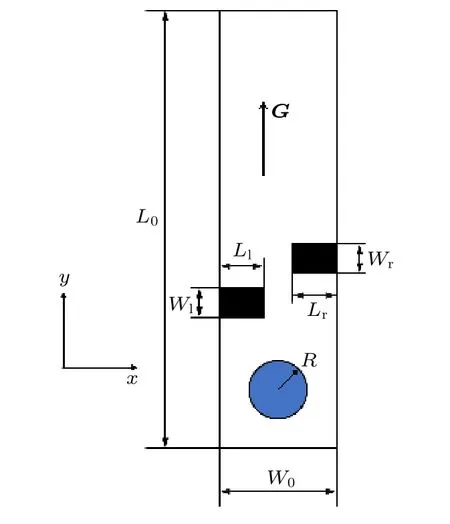
圖2 物理模型Fig.2.Physical model.

其表征浮力與表面張力的相對大小.在下文中，為了描述氣泡宏觀的運動特性，需要用到氣泡的剩余質(zhì)量比、氣泡的上升速度以及氣泡通過時間，定義如下:1)氣泡的剩余質(zhì)量比(De) .氣泡達到通道頂端時的剩余質(zhì)量與最初時刻的質(zhì)量比.剩余質(zhì)量可以通過計算初始氣泡質(zhì)量減去殘留在障礙物表面上的質(zhì)量獲得，而氣泡質(zhì)量可以用計算區(qū)域內(nèi)氣相區(qū)所有格點上的質(zhì)量求和得到，其中氣相區(qū)定義為φ ＜0.5所在的區(qū)域.2)氣泡的上升/速度(Vb).氣泡在y方向的上升速度，其中x為計算區(qū)域內(nèi)的所有格點，uy為速度在y方向的分量.3)氣泡通過時間(T).氣泡從開始運動到運動到通道出口處所需的時間.本文選取2R為特征長度、為特征速度、為 特征時間，分別對與長度、速度和時間相關的量進行無量綱化處理，對應的無量綱量用原符號加星號上標表示.

5 結(jié)果與討論

下面研究大密度比氣泡在含非對稱障礙物通道中的運動行為.氣泡的運動行為受很多因素的影響，如障礙物的相對位置、障礙物之間孔徑大小、氣液兩相的黏度比、浮力和表面張力的相對大小等.本文主要研究Eo數(shù)、氣液兩相黏度比、障礙物的縱向距離、橫向距離以及障礙物的相對大小對氣泡運動行為的影響.數(shù)值模擬中ρg1 ，ρl1000，μl100，μg1.0，M0.1，σ0.312，Φl1 ，Φg0，W080，L0300，R20，W4，g3.9×10-6，氣泡圓心位置為 (40，40)，松弛時間τf和τg可通過(16)式和(17)式根據(jù)給定的遷移率以及流體黏度得到.需要指出的是，以上參數(shù)的單位均為格子單位，關于格子單位和物理單位之間的轉(zhuǎn)換有興趣的讀者可以參閱文獻[37，38].

5.1Eo 數(shù)的影響

本小節(jié)研究表征浮力和表面張力相對大小的Eo數(shù)對氣泡運動行為的影響，在數(shù)值模擬中主要考慮了六種Eo數(shù)的情況:Eo5，10，15，20，25，30 .其他參數(shù)設置如下:LlLr30，WlWr20，兩障礙物底邊與管道左右壁面的交點分別為(0，90)和 (0，120)，不同的Eo數(shù)通過調(diào)節(jié)表面張力的大小得到.

圖3 描述了Eo5，15，20 時氣泡在管道內(nèi)不同時刻的形態(tài)變化.如圖3(a)所示，當Eo5 時，氣泡在即將觸碰到左側(cè)障礙物時(t*9.379)，其左上側(cè)開始稍有變形，略微向內(nèi)凹陷;氣泡在穿過障礙物的過程中(t*15.632—19.072)受到左右兩側(cè)障礙物的擠壓，其頂端仍然基本保持了圓形;當氣泡完全突破障礙物時，其與左側(cè)障礙物發(fā)生拉扯，尾部出現(xiàn)小尖角(t*25.325);隨后氣泡在浮力的作用下完全與障礙物脫離，脫離后的氣泡繼續(xù)上升，由于氣泡在穿過障礙物的過程中形變較小，當它穿過障礙后(t*36.580)，在很短的時間內(nèi)(Δt*2.501)恢復了圓形.當Eo數(shù)增大到15 時(如圖3(b)所示)，氣泡在通過障礙物的過程中變成了長條形(圖3(b)中t*17.508 時刻);當氣泡與障礙物脫離時，在左側(cè)障礙物表面留下了微小的氣泡.Eo數(shù)增加到20 時(如圖3(c)所示)，氣泡與左側(cè)障礙物分離時在左側(cè)障礙物表面留下一個殘留小氣泡，隨后右邊有一部分氣泡觸碰到障礙物后粘在障礙物表面(t*23.761—27.513);當氣泡與右側(cè)障礙物脫離后其在右側(cè)障礙物表面也殘留一個小氣泡.綜上所述，隨著Eo增加，氣泡在穿過障礙物通道過程中分裂的次數(shù)增加，該現(xiàn)象與前人研究結(jié)果[25]一致.此外，隨著Eo數(shù)增加，氣泡在運動過程中形變越來越明顯，這是因為表面張力隨著Eo數(shù)的增加而減小，導致氣泡在運動過程中更容易發(fā)生形變，以上結(jié)論與Alizadeh 等[20]的研究結(jié)果一致.

圖3 不同 Eo數(shù)下的氣泡形態(tài) (a) Eo=5;(b) Eo=15 ;(c)Eo=20Fig.3.Bubble shapes at different values of Eo number:(a) Eo=5 ;(b) Eo=15 ;(c) Eo=20 .

從圖3 還可以看出，Eo數(shù)除了影響氣泡的形狀外，還對氣泡穿過障礙物的時間有很大的影響.為了進一步研究Eo數(shù)對氣泡運動特性的影響，圖4給出了不同Eo數(shù)下氣泡的上升速度隨時間的變化過程.可以看出，氣泡在通道內(nèi)的運動過程與氣泡在運動過程中的狀態(tài)變化一一對應.不失一般性，以Eo20 為例，當氣泡距離障礙物較遠時氣泡在運動過程中速度逐漸增加;當氣泡接近障礙物時受到障礙物的阻礙作用，速度出現(xiàn)了小幅下降(t*2.814—7.816);當氣泡頂端突破障礙物的最小間隙后(t*14.382)，氣泡的速度快速增加，并在t*17.508時達到了最大值，其峰值為0.00376.對比圖3(c)可知，此時由于右邊障礙物對氣泡的黏附力，隨后其形狀進一步發(fā)生變化，對應的速度也開始迅速下降，速度下降的趨勢持續(xù)到t*23.761，此時氣泡突然離開障礙物，隨后在一小段時間區(qū)間內(nèi)(t*23.761—27.513)速度開始有所增加，形成了第二個局部的速度峰值.同時由于氣泡離開障礙物時被擠壓成極不規(guī)則的形狀，當其離開障礙物后，氣泡的形狀在一段時間內(nèi)(t*27.513—36.580)隨著通道截面積增加會迅速發(fā)生變化以盡可能收縮成圓形，因此速度出現(xiàn)小幅度下降.隨后氣泡在浮力和表面張力的作用下，一邊變形一邊上升，速度又一次出現(xiàn)小幅度下降.從以上結(jié)果可以看出，氣泡微觀的界面變化直接影響氣泡宏觀的運動速度.

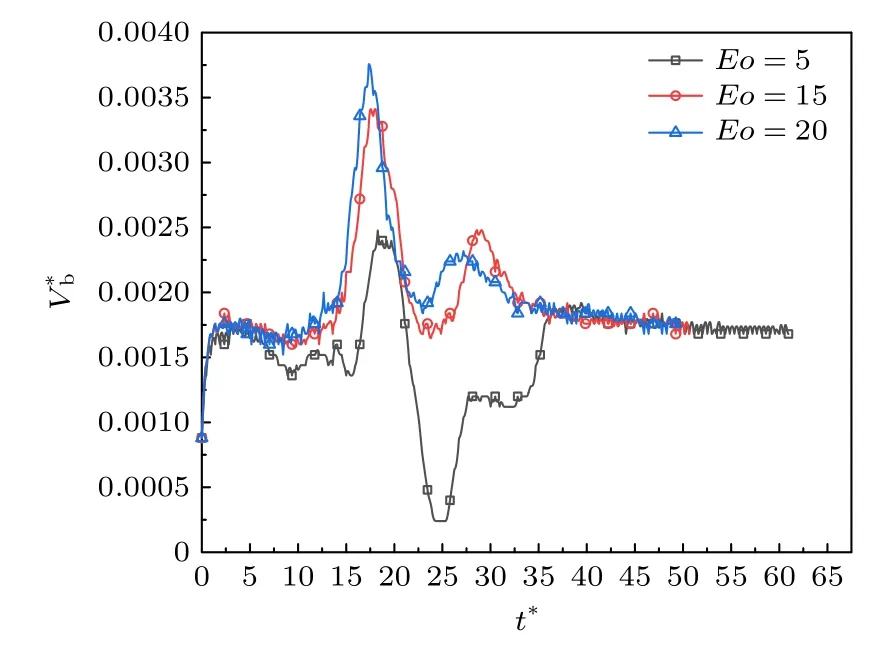
圖4 不同 Eo 數(shù)下氣泡的上升速度Fig.4.Bubble velocity at different values of Eo number.

從圖3 還可以看出，隨著Eo數(shù)增加，氣泡穿過障礙物需要的時間減小，且氣泡在穿過障礙物之后依次出現(xiàn)了“完全與障礙物脫離”、“在左側(cè)障礙物表面殘留小氣泡”、“在左右兩側(cè)障礙物表面都殘留氣泡”幾種情況，說明Eo數(shù)對氣泡穿過障礙物的時間和質(zhì)量都有影響.為了說明這一現(xiàn)象，圖5 給出了不同Eo數(shù)時得到的氣泡剩余質(zhì)量比De以及氣泡穿過障礙物的時間T*.可以看出，Eo數(shù)越大，氣泡穿過障礙物的時間越短.具體地說，當Eo數(shù)較小時，Eo數(shù)的增加能夠大幅減小氣泡通過時間，而當Eo數(shù)增加到15 之后，氣泡穿過障礙物的時間隨著Eo數(shù)的增加緩慢減小.另一方面，當Eo數(shù)較小時，氣泡能全部穿過障礙物，此時氣泡的剩余質(zhì)量比不隨Eo數(shù)的增加而改變.隨著Eo數(shù)的增加，氣泡會依次殘留在左邊障礙物以及左右兩邊障礙物表面，此時氣泡剩余質(zhì)量比隨Eo數(shù)的增加快速減小，而當Eo數(shù)增加到一定值時(Eo20)，氣泡的剩余質(zhì)量比的減少趨于平緩.這是因為當Eo20 時，氣泡在穿過障礙物的過程中已經(jīng)在左右障礙物表面各留下一個殘留小氣泡，隨著Eo數(shù)的進一步增加，盡管氣泡所受的浮力相對于表面張力更大，然而氣泡殘留在障礙物表面的質(zhì)量增加并不明顯.

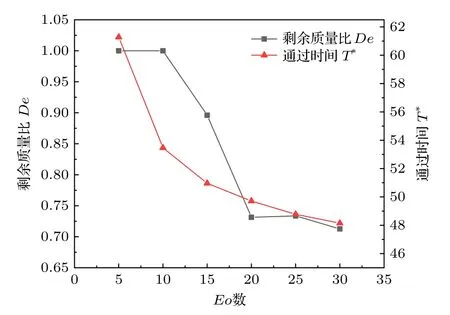
圖5 不同 Eo 數(shù)下氣泡的剩余質(zhì)量比和通過時間Fig.5.Rate of residual mass and passing time of bubble at different values of Eo number.

5.2 黏度比的影響

本節(jié)探究黏度比對氣泡上升過程中形態(tài)變化的影響.數(shù)值模擬中保持氣體黏度不變ug1.0，通過設置不同的液體黏度而得到不同的黏度比，下文中ul分別為設置為10，50，100，150，200，對應的黏度比Mug/ul為0.1000，0.0200，0.0100，0.0068，0.0050.本節(jié)中Eo20，其他參數(shù)設置與5.2 節(jié)相同.

圖6 給出了氣液黏度比為0.1000 時氣泡在關鍵時刻的形狀以及氣泡在上升過程中速度隨時間的變化趨勢.如圖6 所示，氣泡在穿過障礙物的過程中一共被分成五部分，該現(xiàn)象與文獻[39-41]發(fā)現(xiàn)的氣相與液相的黏度比越大，氣泡變形越嚴重結(jié)論一致.具體地說，當氣泡脫離左側(cè)障礙物時產(chǎn)生第一次分離，此時在左側(cè)障礙物表面上留下三個孤立的小氣泡，而當氣泡與右側(cè)障礙物分離時又在該障礙物表面留下一個小氣泡.另一方面，氣泡上升過程中速度也發(fā)生了很大的變化.從初始時刻到t*4.846，氣泡與障礙物通道的距離較遠，速度在上升過程中隨時間增加.當t*4.846 時，氣泡接近障礙物通道，此時速度達到第一個峰值(速度峰值為0.00824).隨后在t*4.846—5.628 的一段時間，氣泡的形狀開始快速變化，對應的速度隨時間減小.在t*5.628—7.035 區(qū)間內(nèi)，氣泡穿過障礙物最小間隙，速度開始上升，并在t*7.035 時速度達到了第二個峰值(峰值為0.00888).此時，氣泡下部與左右障礙物接觸，被拉扯成細長狀.隨后左側(cè)障礙物對氣泡的黏附力使得氣泡的上升速度下降(t*7.035—8.129).在氣泡與左側(cè)障礙物分離后的很短時間內(nèi)(t*8.129—9.067)氣泡的速度又出現(xiàn)了小幅度上升.從t*9.067到t*10.474，氣泡黏附在右側(cè)障礙物表面上，導致其速度又一次減小.隨后氣泡突然脫離障礙物(t*10.474)，速度迅速增加并在t*12.506 時達到了第四個峰值0.0106.由于氣泡在脫離前被右側(cè)障礙物拉扯，其與障礙物脫離時變形嚴重，尾部出現(xiàn)小尾巴狀，隨后在表面張力的作用下氣泡的小尾巴逐漸消失，同時速度出現(xiàn)小幅度下降(t*12.506—14.851)，氣泡在t*14.851 時呈現(xiàn)向右傾斜的月牙形，傾斜的程度在t*12.506—17.821 時間段內(nèi)逐漸減小，速度在t*17.821 時提升到了0.0103，隨后氣泡的速度略有下降，最終氣泡在t*19.853 時到達了通道頂端.

圖6 黏度比 M=0.1000 時的速度變化Fig.6.Bubble velocity at the viscosity ratio M=0.1000 .

其他四種情況下氣泡的上升速度隨時間的變化過程以及氣泡在即將到達頂端時的運動形態(tài)如圖7 所示.相似地，對于不同黏度比的情況，氣泡上升速度的變化都呈現(xiàn)增大-減小-增大-減小-增大-減小-近似不變的趨勢.然而不同黏度比下的速度值有較大差異，黏度比越大，氣泡在上升過程中的速度也越大.這是因為液相的黏度隨著黏度比的增加而減小，使得氣泡在上升過程中受到的阻力減小.黏度比M0.0200 時的速度最大值為0.00536，且氣泡接近通道頂端的速度為0.00312，是M0.0100時對應速度的1.86 倍.另一方面，氣泡穿過障礙物通道后速度近似不變，該近似不變的速度隨著黏度比的增加而增加.例如，當t*＞ 25 后，黏度比M0.0200時，接近通道頂端時氣泡的穩(wěn)定速度約為0.00328.而黏度比M0.0100，0.0068，0.0050 時，接近通道頂端時氣泡的速度分別為0.00192，0.00128，0.000960，遠小于M0.0200 的情況.此外，氣泡穿過障礙物區(qū)域后，從氣泡即將到達出口時的形態(tài)圖可以發(fā)現(xiàn)，殘留氣泡的面積隨著黏度比的增大而增加.氣泡在小黏度比下更能保持圓形，而在大黏度比下氣泡的下方有向內(nèi)凹陷的趨勢.

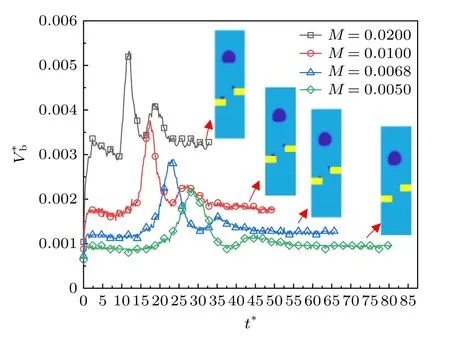
圖7 不同黏度比下氣泡的速度Fig.7.Bubble velocity at different values of viscosity ratio.

圖8 給出了不同黏度比下氣泡的剩余質(zhì)量比和通過障礙物的時間.可以看出，氣泡的剩余質(zhì)量和通過障礙物的時間都隨著黏度比的增加而降低.當黏度比為0.0050 時，氣泡剩余質(zhì)量比高達0.98，說明此時障礙物表面上只殘留了很小一部分氣泡，當黏度比增大到0.0068 時，剩余質(zhì)量比為0.75，減小了23%.隨著黏度比繼續(xù)增大，剩余質(zhì)量比近似線性減小.另一方面，氣泡通過障礙物的時間隨著黏度比的增大先快速減小然后緩慢減小.在黏度比為0.1000 的情況下氣泡穿過障礙的時間為19.853，而在黏度比為0.0050 的情況下，氣泡穿過障礙物的時間為80.976.即當黏度比從0.1 減小到0.005時，氣泡穿過障礙物的時間增加了307.9%.

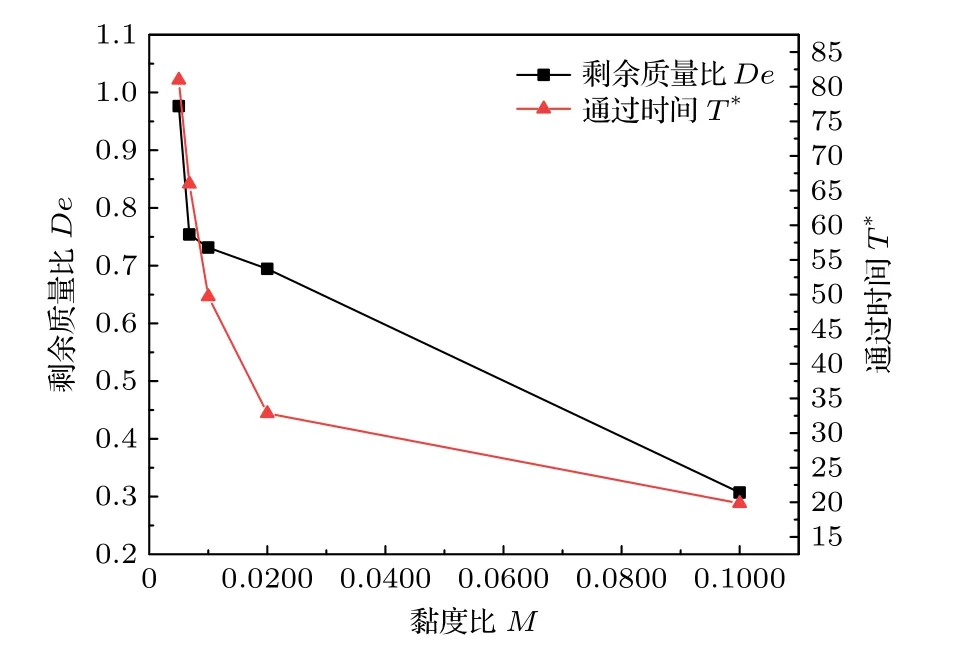
圖8 不同黏度比下氣泡的剩余質(zhì)量比和通過時間Fig.8.Rate of residual mass and passing time of bubble at different values of viscosity ratio.

5.3 障礙物縱向距離的影響

由于實際問題中通道內(nèi)障礙物的大小和位置非常復雜，本小節(jié)研究障礙物的縱向距離對氣泡動力學行為的影響.這里障礙物的縱向距離y1用左右障礙物底邊在y方向的距離來測量.在數(shù)值模擬中，兩障礙物的長度LlLr30，寬度WlWr20，兩障礙物橫向距離為20，保持兩障礙物大小以及左側(cè)障礙物位置不變，通過調(diào)節(jié)右側(cè)障礙物的位置得到不同的障礙物縱向距離，并考慮以下9 種不同的情況，即無量綱縱向距離分別取0，0.125，0.25，0.375，0.5，0.625，0.75，0.875，1.對于所有的不同縱向距離的情況，Eo20，其他參數(shù)的設置與 5.1 節(jié)相同.

圖9 給出了不同障礙物位置得到的氣泡剩余質(zhì)量比和穿過障礙物的時間.障礙物縱向距離的增大并不能總是使氣泡的剩余質(zhì)量增加.當氣泡的縱向距離為0 和0.125 時，氣泡的剩余質(zhì)量比相差較小，當縱向距離在 0.125—0.375 范圍內(nèi)時，剩余質(zhì)量隨著縱向距離增大急劇增加，當縱向距離在0.375—0.75范圍內(nèi)時，剩余質(zhì)量隨著縱向距離增大迅速減小，而當縱向距離在 0.75—1 范圍內(nèi)時，剩余質(zhì)量隨著縱向距離增大而增加.在0.75 時剩余質(zhì)量最小，即障礙物上附著氣泡質(zhì)量最大.為了進一步闡釋氣泡質(zhì)量的變化規(guī)律，圖10 給出了同一時刻不同障礙物縱向距離時得到的殘留氣泡的大小和位置，可以看出，隨著縱向距離的增加，氣泡分布位置的改變影響了氣泡的剩余質(zhì)量比.具體地說，在障礙物縱向距離小于0.375 時，殘留在左右障礙物下方的氣泡隨著障礙物縱向距離的增加而減少.在這個范圍內(nèi)，距離的增大有利于氣泡通過障礙物，從而減少殘留氣泡的質(zhì)量.當左右障礙物縱向距離增大至0.5 時，左邊障礙物除了底部外，其側(cè)面也出現(xiàn)少量氣泡殘留.此時，距離的增加并不能減少障礙物上的殘留物，反而因為氣泡和左邊障礙物的接觸面積增加使得氣泡的殘留質(zhì)量增加，導致氣泡剩余質(zhì)量減少.當障礙物的距離增加到0.625 時，右邊障礙物除了底面外，其左側(cè)面也出現(xiàn)了氣泡殘留.0.75 時，左右障礙物下方的殘留氣泡消失，然而上方殘留的氣泡更多，此時氣泡剩余質(zhì)量比繼續(xù)減小，值為0.73.而當障礙物縱向距離大于0.75 時，氣泡剩余質(zhì)量比開始增加.這是由于當障礙物縱向距離增加到一定程度時，氣泡穿過左邊障礙物之后，通道越大氣泡與右側(cè)障礙物的接觸面積越少，甚至不與右邊障礙物下表面發(fā)生接觸(1)，使得殘留在障礙物表面的氣泡質(zhì)量減少.

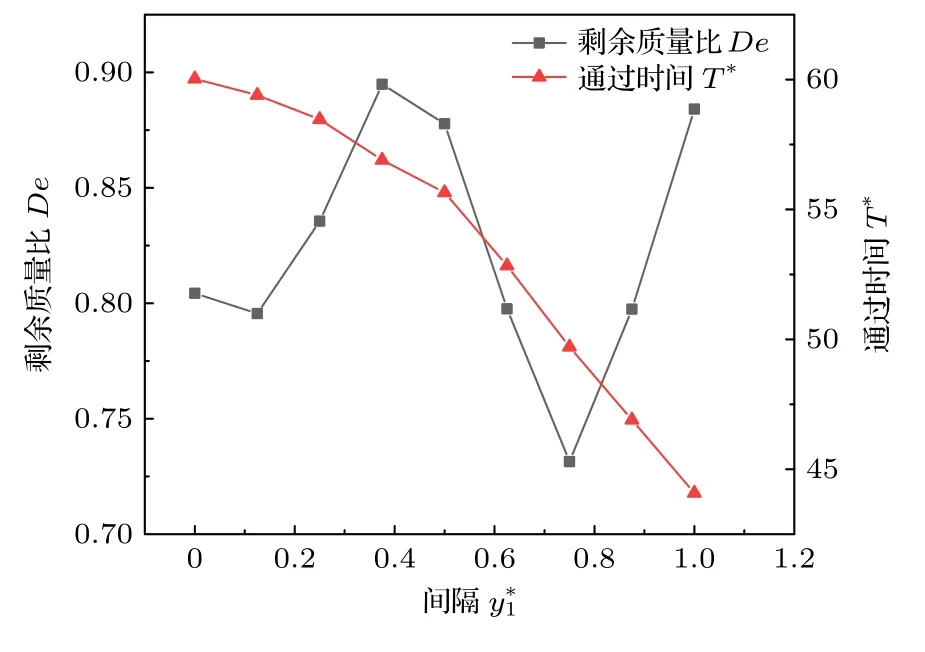
圖9 不同障礙物縱向距離下氣泡的剩余質(zhì)量比和通過時間Fig.9.Rate of residual mass and passing time of bubble at different vertical distances between the obstacles.

圖10 不同障礙物縱向距離在同一時刻下氣泡穿過障礙物后的形態(tài)Fig.10.Bubble shape after passing through obstacles under different vertical distances between the obstacles at the same time.

另一方面，從圖9 還可以發(fā)現(xiàn)，氣泡通過障礙物的時間隨著障礙物縱向距離的增加而減少.為了闡明引起這一現(xiàn)象的原因，圖11 給出了不同障礙物縱向距離時氣泡的上升速度.從圖11 結(jié)果可知，障礙物縱向距離越大，氣泡上升初期的速度增長幅度越大，同時氣泡接近通道頂端的速度也越大.另一方面，當障礙物縱向距離小于0.5 時，在氣泡快要觸碰到障礙物時，有明顯的速度減小段，而在障礙物距離大于0.5 的時候，速度減小的程度不明顯.這是因為兩障礙物之間的縱向距離越大，氣泡在遇到第一個障礙物時有更多朝右側(cè)避讓的空間，氣泡所受的阻礙力減少.此外，對于所有的情況，當氣泡完全穿過障礙物最小間隙后速度迅速下降，且縱向距離越大，氣泡速度減少的程度越小.這是由于縱向距離較大時，氣泡和右邊障礙物的接觸更少，所受的黏附力減小，速度下降的幅度也更小.

圖11 不同障礙物縱向距離下氣泡的速度Fig.11.Velocity of bubble at different vertical distances between the obstacles.

5.4 障礙物橫向距離的影響

本小節(jié)進一步研究障礙物橫向距離x1對氣泡運動行為的影響.這里障礙物的橫向距離x1指的是兩障礙物在水平方向的距離，可以通過通道寬度減去兩障礙物長度之和得到.為了得到不同的障礙物橫向距離，主要考慮如下兩種情況.Case A:左右障礙物長度相同，通過同時改變兩側(cè)障礙物長度而得到不同的橫向距離.Case B:保持左側(cè)障礙物不變，只改變右側(cè)障礙物的長度而得到不同的障礙物橫向距離，對于以上兩種情況都保持障礙物縱向距離y130 不變.

5.4.1 Case A:同時改變左右側(cè)障礙物的長度

本節(jié)設置8 種不同障礙物情況:分別為0.7，0.6，0.5，0.4，0.3，0.2，0.1，0，其他參數(shù)設置與5.1 節(jié)中Eo20 的情況相同.

圖12 障礙物橫向距離=0 時氣泡的速度(Case A)Fig.12.Velocity of bubble at the horizontal distance=0(Case A).

圖13 給出了其他七種情況下氣泡在上升過程中的變化過程.從圖13 結(jié)果可知，當障礙物橫向距離小于0.6 時，氣泡在上升過程中速度的變化趨勢與前面小節(jié)中相同，都為增大-減小-增大-減小-增大-減小.而當橫向距離增加到0.7 時，氣泡在上升過程中的變化趨勢為增大-減小-增大-減小.這是因為隨著橫向距離的增加，氣泡在靠近障礙物時其速度不再下降，且氣泡在完全穿過障礙物后其形變不明顯使得速度下降也不明顯.為了說明這一點，圖14 給出了不同障礙物橫向距離時氣泡在即將脫離障礙物時的運動形態(tài).可以看出，當距離=0.7時，氣泡到達第二個障礙物時幾乎沒有與障礙物接觸，其頭部保持了圓形而尾部也只是發(fā)生了略微變形，因此氣泡靠近障礙物時(t*1.876—8.286)速度上升趨勢僅僅是減緩而不是明顯的下降.另一方面，氣泡穿過障礙物以后，對于橫向距離小于0.6 的情況，由于障礙物通道較小，氣泡受到的擠壓力較大，氣泡在穿過障礙物通道時其尾部被拉成了“逗號”的形狀，而且障礙物的橫向距離越小，“逗號”的尾巴越長.以上現(xiàn)象說明障礙物的橫向距離越小，氣泡受到的擠壓力越大，因此氣泡速度下降的幅度也越大.具體地說，當氣泡靠近障礙物時，障礙物橫向距離=0.6時氣泡速度從t*1.251時刻的0.00232，下降到了t*7.503 時的0.00216，只下降了6.9%.而在橫向距離=0.2 時，速度從t*1.407時刻的0.000960，下降到了t*7.503 時的0.000240，下降了75.0%.

圖13 不同障礙物橫向距離下氣泡的速度變化(Case A)Fig.13.Velocity of bubble at different horizontal distances between the obstacles (Case A).

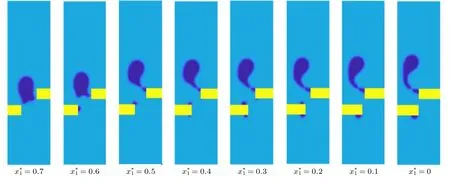
圖14 不同障礙物橫向距離下氣泡即將脫離障礙物時的形態(tài)(Case A)Fig.14.Bubble shape of leaving obstacles at different horizontal distances between the obstacles (Case A).

圖15 給出了Case A 在不同橫向距離下得到的氣泡剩余質(zhì)量比和通過障礙物的時間.從圖15結(jié)果可以發(fā)現(xiàn)，當障礙物橫向距離小于0.3 時，氣泡的剩余質(zhì)量比變化不明顯，當橫向距離大于0.3時，氣泡剩余質(zhì)量比開始出現(xiàn)明顯的增長趨勢，當橫向距離=0.7 時，氣泡剩余質(zhì)量比為1，說明氣泡全部穿過了障礙物沒有任何殘留，這是因為隨著障礙物橫向距離的增加，氣泡更容易通過障礙物通道.從圖15 還可以發(fā)現(xiàn)一個有趣的現(xiàn)象，即橫向距離為0.5 時的氣泡剩余質(zhì)量比略小于橫向距離為0.4 時得到的值，這是因為橫向距離從0.4 增加到0.5 的過程中，氣泡與左側(cè)障礙物接觸面積增加，導致殘留在左側(cè)障礙物表面上的氣泡質(zhì)量增加(如圖14 所示).另一方面，不同障礙物橫向距離得到的氣泡通過障礙物的時間隨著橫向距離的增大而近似線性減小，距離為=0 時，氣泡所需通過時間最大(T*84.728)，距離為=0.7 時，氣泡的通過時間最小(T*40.019).

圖15 不同障礙物橫向距離下氣泡的剩余質(zhì)量比和通過時間(Case A)Fig.15.Rate of residual mass and passing time of bubble at different horizontal distances between the obstacles (Case A).

5.4.2 Case B:改變單個障礙物的長度

本小節(jié)通過改變右側(cè)障礙物的長度Lr來研究障礙物橫向距離對氣泡運動行為的影響，分別考慮了右側(cè)障礙物長度x1為34，38，42，46，50 這五種情況，對應的障礙物間的無量綱橫向距離分別為0.4，0.3，0.2，0.1，0.數(shù)值模擬中其他參數(shù)的設置與5.4.1 小節(jié)中情況相同.

圖16 給出了Case B (改變右側(cè)障礙物長度)情況下當障礙物橫向距離0 時得到的氣泡上升速度和關鍵位置形狀圖.對比圖12 (Case A)和圖16 可知，盡管兩種情況障礙物通道的橫向距離都是0，但是由于障礙物結(jié)構(gòu)不同，導致氣泡的運動形態(tài)有很大變化.首先，對于Case A，氣泡在穿過障礙物通道后分裂成四個小氣泡，其中一個出現(xiàn)在左側(cè)障礙物處，一個出現(xiàn)在右側(cè)障礙物處，另外兩個出現(xiàn)在障礙物上方.而對于Case B，氣泡穿過障礙物通道后也分裂成了四部分，但是其中兩個小氣泡出現(xiàn)在右側(cè)障礙物表面，剩下一大一小的兩個氣泡出現(xiàn)在障礙物上方的通道中.同時，Case B 出現(xiàn)在障礙物上方的兩個氣泡的位置都比較靠近通道左側(cè)，尤其是尺寸較小的氣泡，幾乎貼在了通道左側(cè)壁面上.

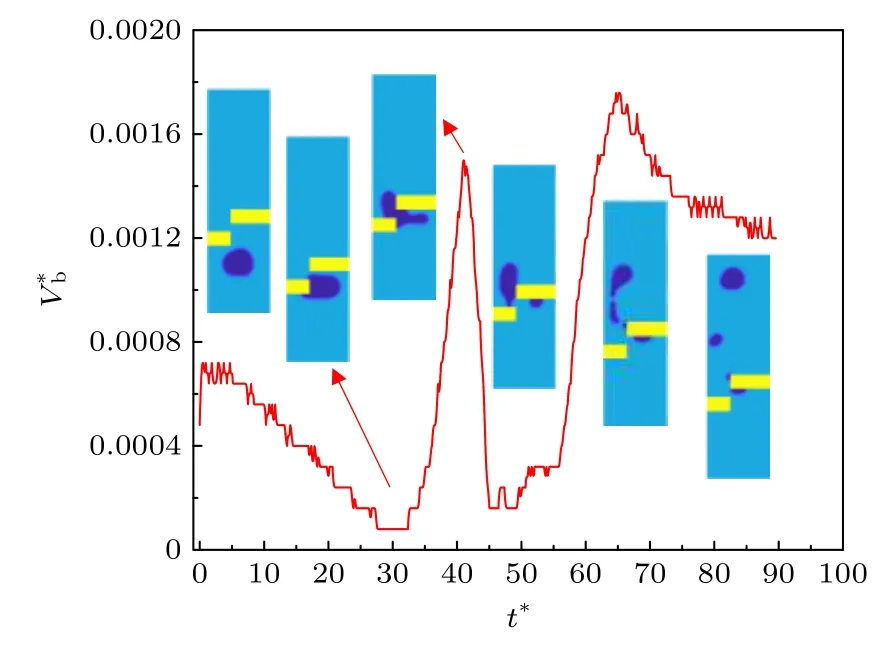
圖16 障礙物橫向距離=0 時氣泡的速度(Case B)Fig.16.Velocity of bubble at the horizontal distance=0(Case B).

為了直觀地描述兩種情況下氣泡運動的區(qū)別，圖17 給出了不同情況下得到的氣泡通過障礙物的時間.從圖17 結(jié)果可知，對于Case A 和Case B，都有隨著障礙物距離的增大，氣泡通過時間明顯減少.而且在氣泡距離大于等于0.3 時，氣泡在兩種情況下的通過時間幾乎一致，但在障礙物橫向距離小于0.3 時，Case B 得到的氣泡穿過障礙物的時間小于Case A 得到的穿過時間，并且隨著橫向距離的減小，它們之間的差距越大.在=0 的情況下，Case A 得到的氣泡穿過障礙物的時間為 84.728，而Case B 的穿過時間為 89.731 .

圖17 Case A 和Case B 的氣泡通過時間對比Fig.17.Comparison of the passing time of the bubble between the Case A and Case B.

圖18 給出了兩種情況下得到的氣泡剩余質(zhì)量比.當障礙物橫向距離小于0.2 時，Case A 的剩余質(zhì)量大于Case B 的剩余質(zhì)量比.這是因為對于Case B，距離小于0.2 時，氣泡受到右邊障礙物的阻礙力更大，有一大部分氣泡被殘留在了右側(cè)障礙物下方，例如圖16 中右邊障礙物下方氣泡殘留比圖12 更多.當距離大于0.2 時，Case B 的剩余質(zhì)量明顯大于Case A.這是因為對于Case B，由于左側(cè)障礙尺寸較小，當障礙物橫向距離增加時，氣泡幾乎不與左側(cè)障礙物接觸，從而不會有氣泡殘留在左側(cè)障礙物表面.

圖18 Case A 和Case B 的剩余質(zhì)量比對比Fig.18.Comparison of the rate of residual mass between the Case A and Case B.

5.4.3 寬度的影響

本節(jié)繼續(xù)研究障礙物結(jié)構(gòu)對氣泡運動過程的影響.這里固定左邊障礙物的大小和位置，以及右邊障礙物底邊的位置和長度，調(diào)節(jié)右邊障礙物的寬度Wr探究左右障礙物寬度不同時氣泡運動行為.在數(shù)值模擬中，主要考慮了七種情況，0.25，0.375，0.5， 0.625， 0.75， 0.875， 1，其他參數(shù)的設置與5.1 小節(jié)中Eo20 的情況相同.

圖19 給出了不同的右側(cè)障礙物寬度情況下得到的氣泡剩余質(zhì)量以及通過障礙物的時間.從圖19結(jié)果可看出，隨著右側(cè)障礙物寬度增加，氣泡通過障礙物的時間逐漸增加，但是增加的幅度不大.在考慮的最小寬度情況下(0.25)，通過時間T*49.399，而在寬度最大時(1)，T*50.649，相較于寬度為0.25 的情況，通過時間僅增加了2.53%.此外，氣泡的剩余質(zhì)量比隨障礙物寬度的變化情況比通過時間的變化情況復雜.首先，隨著障礙物寬度的增加，氣泡剩余質(zhì)量比先小幅度增加然后再急速下降，隨后保持在0.725 附近.為了揭示氣泡剩余質(zhì)量比隨障礙物寬度變化的規(guī)律，圖20給出不同障礙物寬度情況下氣泡離開障礙物通道時的形態(tài).從圖20 可以發(fā)現(xiàn)，當障礙物寬度小于0.375 時，氣泡與障礙物脫離時只在左側(cè)障礙物表面有殘留氣泡.而當障礙物寬度增加到0.5 時，氣泡在與障礙物脫離時在右邊障礙物表面上也開始出現(xiàn)殘留氣泡.圖20 中的結(jié)果還表明，當障礙物寬度超過0.5 后，寬度的增加不影響氣泡的分離位置，即對于右側(cè)障礙物寬度大于等于0.5 的五種情況，氣泡始終是在y*3.5 附近位置與障礙物發(fā)生分離.該現(xiàn)象說明當障礙物橫向距離不變時，障礙物到達足夠的寬度后，寬度的繼續(xù)增加對于氣泡脫離障礙物時的運動形態(tài)影響較小，相應的對氣泡剩余質(zhì)量和通過時間的影響也較小.

圖19 右邊障礙物寬度對氣泡通過時間和剩余質(zhì)量比的影響Fig.19.Influence of the width of the right obstacle on the rate of residual mass and the passing time of the bubble.

圖20 右側(cè)障礙物寬度不同時氣泡與障礙物分離時的形態(tài)Fig.20.Shape of bubble departing from the obstacle with different widths of the right obstacle.

6 結(jié)論

本文采用LB 方法模擬大密度比氣泡在含非對稱障礙物微通道內(nèi)的變形、分裂以及上升的運動行為.主要研究了不同Eo數(shù)、黏度比、障礙物的相對位置、形狀、以及尺寸對微通道內(nèi)氣泡的運動形態(tài)、上升速度、通過時間、剩余質(zhì)量的影響，主要得到以下結(jié)論:

1)氣泡在運動過程中的速度變化趨勢由其界面動力學行為決定.

2)Eo數(shù)越小，氣泡在穿過障礙物時變形越小、剩余質(zhì)量比越大、通過時間越長.

3)隨著氣液黏度比的增加，氣泡變形更嚴重，上升速度更快，通過通道的時間更短，且氣泡剩余質(zhì)量比更少.

4)隨著左右障礙物之間縱向距離的增加，殘留氣泡的分布位置發(fā)生了變化，并且導致了剩余質(zhì)量比的變化.氣泡剩余質(zhì)量比隨著障礙物縱向距離的增加先近似不變后增大接著減小再增大，而氣泡通過障礙物的時間隨障礙物縱向距離的增加持續(xù)減小.

5)左右障礙物之間的橫向距離越小，氣泡變形越嚴重、上升速度越小，障礙物側(cè)面氣泡殘留越多.在橫向距離極窄的情況下，單側(cè)障礙物長度改變使氣泡變形更嚴重，通過障礙物時間更長.

6)在障礙物橫向距離固定的條件下，隨著右側(cè)障礙物寬度的增大，氣泡通過障礙物的時間緩慢增加，而氣泡剩余質(zhì)量比先近似不變，然后大幅下降，最后又保持近似不變.另一方面，當右側(cè)障礙物寬度足夠?qū)捄髿馀蓦x開障礙物時的位置幾乎不變.