基于主動阻尼控制的柔性基座振動抑制
周 政,鄒懷武,儲駐港,鐘 樓,湯奇榮
(1.同濟大學機械與能源工程學院 機器人技術與多體系統實驗室,上海 201804;2.上海市空間飛行器機構重點實驗室,上海 201108)
0 引言
隨著空間在軌服務技術的發展,空間機械臂越來越多地被應用到航天器的維修、維護等任務之中。在空間站中,為了增加機械臂的操作空間,有時將其安裝在移動基座上。移動基座先將機械臂移動至目標工作區域后鎖緊,再由機械臂進行更加精細的操作。然而機械臂在運動過程中會不可避免地對基座產生反作用力,使得基座產生振動從而影響機械臂的操作精度。為了保證機械臂能夠平穩操作,需要消除或者補償對基座的反作用力以及力矩。對于柔性基座與機械臂系統的控制策略,共有3 類方法:第1 種方法,從反作用力入手,該方法通過規劃1 條對基座產生反作用力最小的路徑或者設計控制輸入,從而有效地減少對基座的擾動,比如耦合圖、反作用零空間法,但這類方法在受到外部擾動、基座產生振動的情況下不再適用。第2種方法,從機械臂控制入手,利用機械臂的運動來消除基座振動,這種方法存在一系列的缺點,比如控制方法的切換會帶來力矩的突變,從而使得末端偏離穩態位置,對系統結構性能的要求也更高。第3 種方法,從基座的振動控制入手,通過設計系統輸入,在實現機械臂軌跡跟蹤的同時實現基座的振動控制,比如主動阻尼控制、慣性阻尼控制。慣性阻尼控制需要知道系統的頻率特性,但不同的工作位置系統的頻率特性不同。主動阻尼控制需要獲取加速度反饋以及系統的慣性矩陣,但基座運動與機械臂運動可以得到有效解耦,系統可以保持良好的魯棒性。
本文針對主動阻尼控制中系統慣性矩陣估計的問題,利用參數辨識的方法,以獲取系統慣性矩陣較為準確的估計值,并在原始主動阻尼控制的基礎上,添加基座位移補償項以改進抑振效果。最后通過仿真驗證,得到基座振動抑制以及機械臂關節空間軌跡跟蹤結果。
1 柔性基座機械臂的動力學模型與參數辨識
1.1 柔性基座機械臂耦合系統建模
柔性基座機械臂系統簡化模型如圖1 所示,系統由1 個基座與2 關節機械臂組成。

圖1 柔性基座機械臂系統Fig.1 Flexible base manipulator system
根據文獻[11],基座的柔性占主要因素,將機械臂視為剛性,柔性基座為彈簧-質量-阻尼系統,考慮平移位移,忽略旋轉位移。圖中,C
為機械臂的質心,m
為基座的質量,K
為彈簧的剛度系數,C
為阻尼系數。基于這些假設,通過Lagrange 方程建立動力學模型如下:
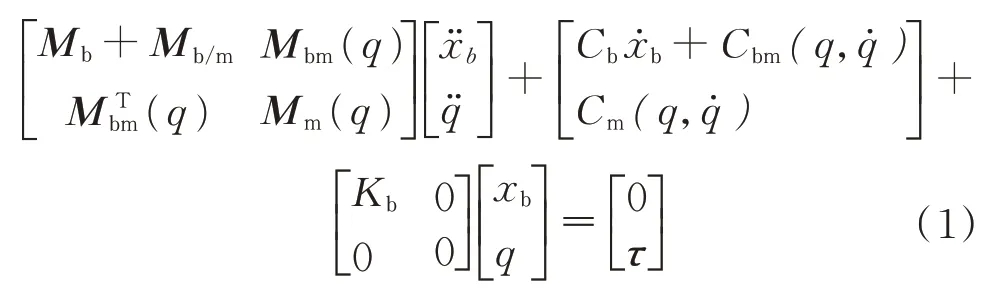
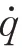
1.2 機械臂參數辨識
一般的機械臂動力學模型如下:
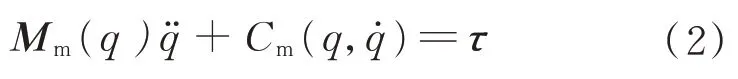
這類模型可以轉化為機械臂慣性參數的線性函數,通過采集機械臂的運動數據,從而建立慣性參數的線性方程組,這樣機械臂參數辨識的問題便轉化為解線性方程組問題,即
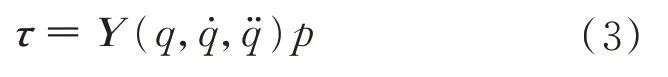
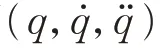
此外,參數辨識的精度與機械臂運動軌跡有關,機械臂按照預定軌跡運動時需要到達盡可能多的位姿和更好的參數辨識效果。有限項傅里葉級數軌跡常作為機械臂參數辨識的激勵軌跡,采用如下公式作為各個關節的激勵軌跡:
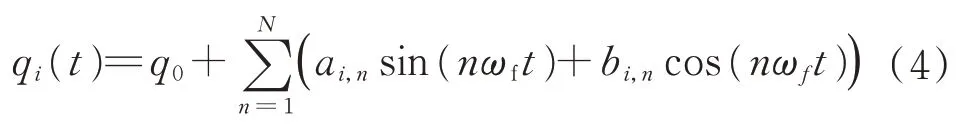
a
、b
、q
分別為傅里葉級數正弦項、余弦項系數、關節補償。
2 控制方案
2.1 機械臂與基座運動解耦
為了能夠將機械臂的運動與基座運動解耦,從而分別對其控制,需要對機械臂的慣性矩陣進行估計。將估計值代入式(1)中的第2 行,得到
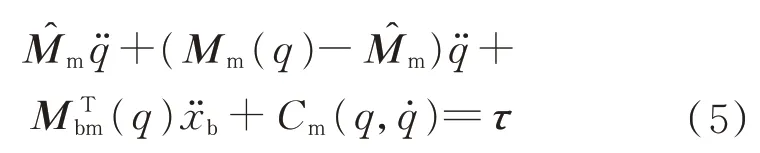
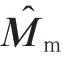
此估計值可由之前參數辨識所獲得的結果得出,顯示表達式為

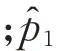
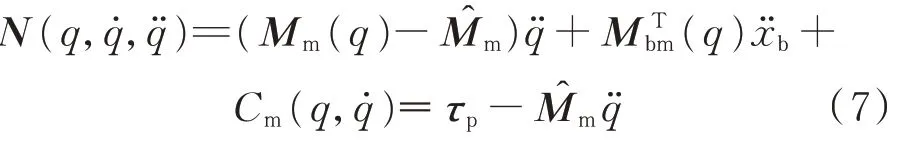
τ
為前一個采樣時刻點的力矩數據,在采樣頻率很高的條件下,可以認為τ
≈τ
。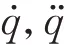
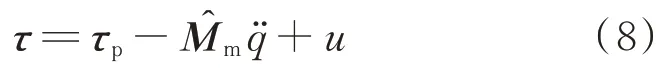
結合式(1)與式(8),將系統慣性矩陣求逆,改寫系統動力學方程為
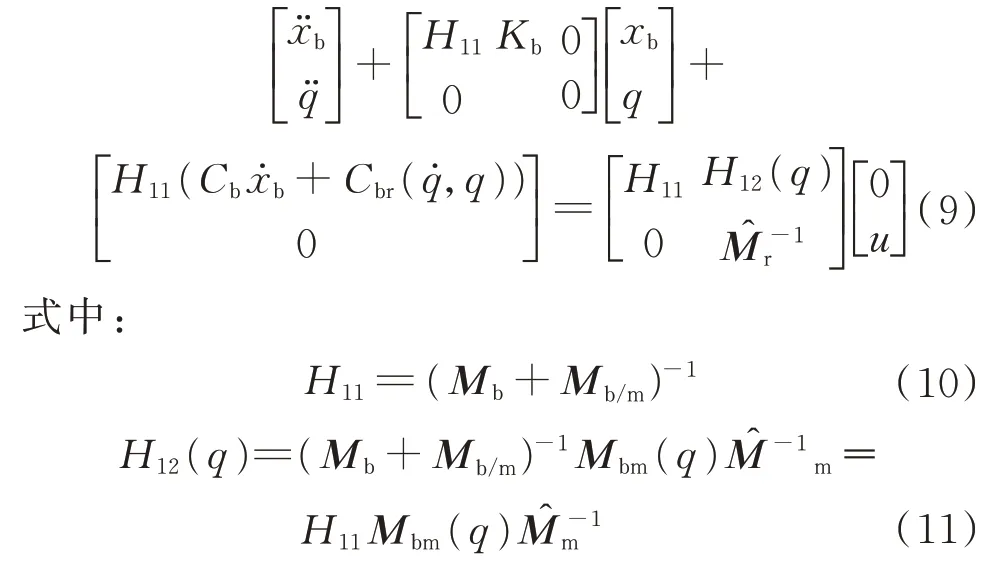
u
決定。2.2 系統控制律設計
一個系統輸入u
需要同時控制2 個變量x
與q
,定義u
由2 個部分組成: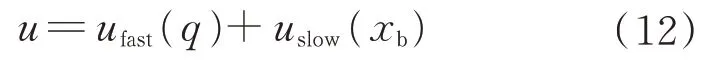
u
(x
)主要作用于基座運動;u
(q
)主要作用于機械臂運動。機械臂軌跡跟蹤控制律的設計利用經典的計算力矩法的思想得出
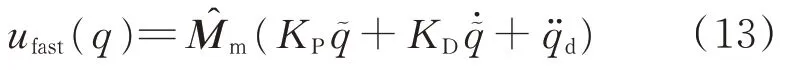

u
(x
)可以當作一個常數,原始的主動阻尼控制原理中基座運動控制輸入為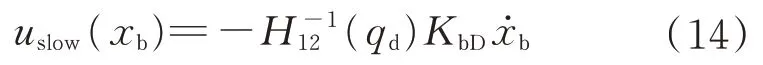
K
為阻尼控制系數。

u
(q
)和u
(x
),得到總控制律為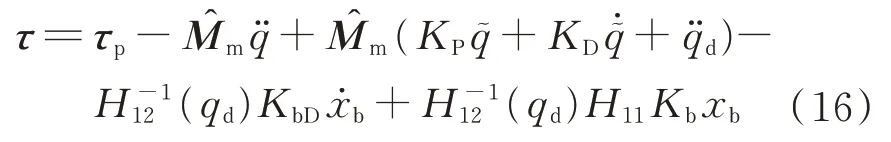
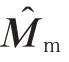
3 仿真試驗及結果分析
考慮如圖1 所示的機械臂系統,機械臂實際參數以及基座的等效模型參數見表1。在仿真過程中,機械臂的關節運動采用5 階多項式,每個關節從0 rad 運動到2 rad,初始和結束時刻速度與加速度為0,運動時間為3 s,并在Simulink 中進行控制效果的驗證。

表1 機械臂系統參數Tab.1 Parameters of the manipulator system
3.1 參數辨識結果
鑒于慣性參數集是非時變的,根據機械臂按照激勵軌跡運動的數據,利用最小二乘法進行估計,辨識結果見表2。

表2 參數辨識結果Tab.2 Results of the parameter identification
此外,利用慣性參數的估計值進行力矩值計算,將各個關節的實際力矩與理論力矩進行對比,以驗證辨識效果,對比結果如圖2 所示。關節1 的平均力矩誤差不超過10%,關節2 的平均力矩誤差不超過2%,動力學參數辨識的結果可以用作后續慣性矩陣的估計。
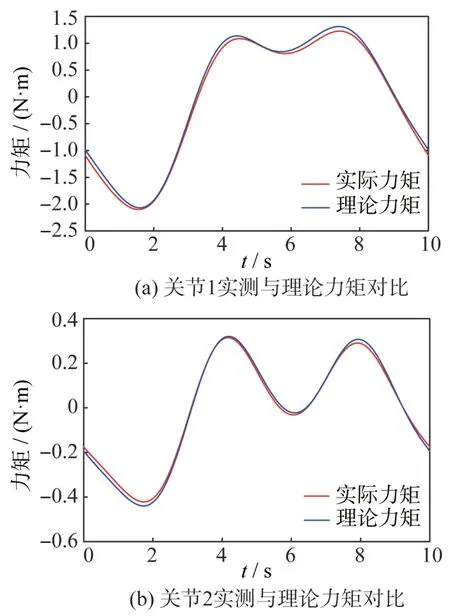
圖2 參數辨識效果驗證Fig.2 Verification of the parameter identification
3.2 基座抑振控制結果
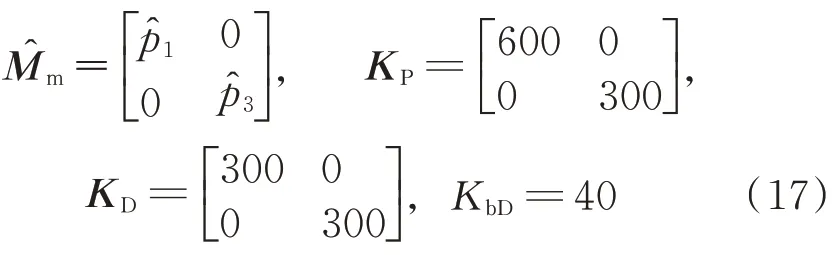
不同控制律下的基座的位移圖像如圖3 所示,可以清楚地看出機械臂關節運動給基座施加了一個用于抑制的阻尼力,根據參數辨識獲取的慣性矩陣可以反映出系統的基本特性,以此設計的基座控制器抑振效果明顯。此外添加基座位移補償項后,雖然在機械臂運動過程中局部振幅變大,但在運動結束后的誤差收斂速度明顯優于改進前的控制律,同時穩態誤差減小了不少。
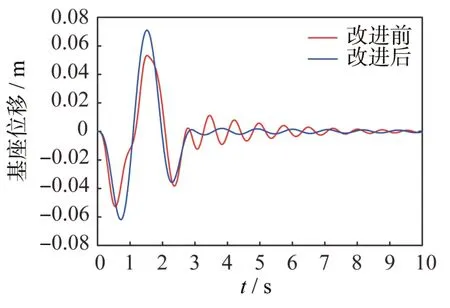
圖3 改進前后控制律下基座位移響應Fig.3 Base displacement responses under the classical and improved control laws
機械臂關節軌跡跟蹤誤差的情況如圖4 和圖5所示。
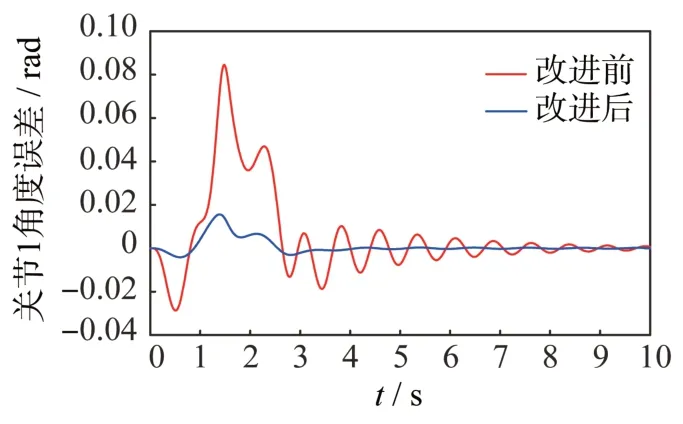
圖4 不同控制律下關節1 角度誤差對比Fig.4 Angle errors of Joint1 under the classical and improved control laws
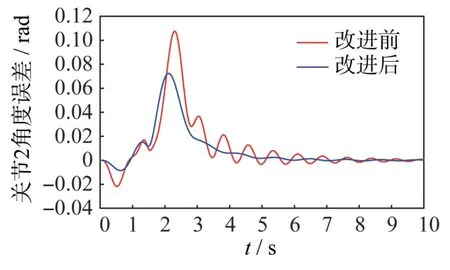
圖5 不同控制律下關節2 角度誤差對比Fig.5 Angle errors of Joint2 under the classical and improved control laws
實際上用于基座抑振的機械臂關節運動是在一個范圍內左右擺動,以此產生相當于阻尼的效果,并且擺動的范圍很小,基本不影響機械臂的正常操作任務。圖中也給出了控制律改進前后的關節角度誤差對比,可見添加了基座位移補償項后獲得了更高的軌跡跟蹤性能,誤差收斂得更快,在運動結束的3 s 左右就完成了基座抑振目標,而改進前需要更長的時間。
4 結束語
主動阻尼控制實質上是利用機械臂的左右擺動產生基座抑振的阻尼力,從而完成柔性基座的控制任務。這類方法控制律設計簡單,并且能夠保證關節空間軌跡跟蹤精度。本文以2 自由度機械臂與彈簧-質量-阻尼的耦合模型為基礎,通過在原始的主動阻尼控制律中加入基座位移補償量,并利用參數辨識的方法估計慣性矩陣。驗證結果表明,改進后的控制律能夠以更快的速度達到誤差收斂,達到了柔性基座振動抑制的目的,證明了方法的有效性,對于拓展到空間大型柔性結構系統有較好的參考價值。

