基于分類搜索的SDN流表無環一致性更新方案①

楊榮寬,張奇支,趙淦森,鄭偉平

1（華南師范大學 計算機學院,廣州 510631）

2（廣州市云計算安全與測評技術重點實驗室,廣州 510631）

1 引言

1.1 研究背景及介紹

SDN（Software-Defined Networking）是一種將網絡控制平面和數據平面分離、具備可編程性的新型網絡架構[1].基于OpenFlow協議的SDN架構將底層基礎設施抽象出來,使用戶能夠通過編程來集中控制網絡轉發行為.當網絡狀態發生變化時,SDN控制器可通過下發新的轉發規則更新交換機流表項,從而管理整個網絡狀態.盡管SDN實現了網絡的集中控制,但數據平面設備的分布式特性也帶來了許多問題,如交換機自身安裝流表項的速度、交換機間的傳輸延遲等.這使得流表項生效時間難以一致,進而導致更新不一致,增加了集中管理的難度[2].

目前,我們正在參與一項國家重點研發計劃子課題的項目研究.該項目的一個主要研究目標是在政務通信網絡中提出一種能保證數據轉發高可靠性、提供細粒度QoS保障的機制.而數據轉發的可靠性和細粒度QoS直接依賴于SDN轉發策略的更新一致性.因此,保證SDN流表更新一致,對保證項目中的數據轉發高可靠性和細粒度QoS具有重大意義.本文在此基礎上,研究能保證SDN流表更新一致、數據可靠轉發、更新性能好的更新方案.

1.2 SDN流表一致性更新

在SDN網絡中,當交換機收到一個數據報后,它首先查找轉發流表.若有匹配的流表項,則執行相應的動作.否則交換機會向控制器發送packetin消息,將報文上報至控制器進行處理.控制器處理后,會向交換機下發新的轉發流表項指導后續轉發.此外,當網絡狀態發生變化時,控制器會主動或被動向交換發送新的轉發流表項,以形成新的轉發路徑[3].

由于數據平面的交換機呈分布式排列,控制器向每臺交換機下發新流表的時延會有不同,交換機內部的更新速度也有差異,這會導致新規則的所有流表項無法同時生效,使數據包出現錯誤的轉發處理,引發數據轉發中斷、環路等問題,影響網絡流量傳輸的可靠性和細粒度QoS的保證.

因此,在新舊規則的更新過程中,必須要保持流表的一致性更新.即控制器在更新交換機中的流表項時,那些正在傳輸的數據包在每個交換機上要么匹配舊規則流表項,要么匹配新規則流表項,不能出現在交換機A上匹配舊規則,而在交換機B上又匹配新規則的情況.為了更好地說明SDN流表更新不一致性引起的問題,下面以圖1進行舉例說明.其中節點Ni（1≤i≤8）代表交換機,實線代表舊轉發路徑,虛線代表新轉發路徑.

圖1 路由更新實例

假設某時刻SDN控制器同時向各個交換機下發更新命令:將轉發規則更新至新路徑.由于控制器和不同交換機的傳輸時延差異,交換機無法同時完成更新.當N1完成更新而N8尚未更新時,即N8沒有匹配數據流的轉發規則,則轉發到N8的數據流將不知作何處理.如果默認動作是丟棄報文,則會引起流中斷.此外,如果交換機N6更新了而N5尚未更新,就會形成環路N6→N5→N6.這會長時間占用鏈路直至報文的TTL超時,從而降低鏈路利用率和轉發性能.

通常來說,SDN流表更新出現不一致時,可能會導致網絡中斷、環路、安全漏洞等問題.為確保從舊規則過渡到新規則期間,網絡能正確轉發報文,則必須要考慮所有可能出現的中間狀態及其屬性[4].很明顯,流表的一致性更新,關系到網絡配置能否正確實現.

目前,針對SDN流表更新一致性問題,研究者已經提出了多種更新方案,如兩階段更新[5]、反向更新[6]、基于分類時序更新[7]、時間觸發更新[8]、分段更新[9]等.

1.3 相關工作

為了確保更新無黑洞和無循環的一致性屬性,Reitblatt等首先提出每流/每包一致性的定義[5],并基于此定義提出了兩階段更新方案進行策略轉發更新.

周曄等[10]、齊嬋等[7]在兩階段更新的基礎上分別提出了基于分類和基于分類時序的流表更新一致性方案,核心均在于根據更新操作類別對交換機進行分類,并按照一定的順序更新規則.不同的是,分類時序更新增加了對流表項的細分操作.分類時序更新雖算法簡單,但其根據嚴格設定的順序來更新新舊轉發路徑上的節點,忽略了同時是新舊路徑上的交換機的情況,存在應用場景局限性.此外,不管更新拓撲復雜與否,都需要等待一定的端到端最長時延才能進行下一階段,方案更新輪次固定,更新時延過長.

基于節點依賴關系,Diogo等[6]提出了反向更新方案.該方案雖算法簡單,但其節點依賴復雜,也沒有考慮節點規則無須更新的情況,嚴格依據新規則轉發路徑從目的節點遞歸向前更新以避免環路.因此,更新輪次多,致使更新時延長.另外,Fu等[11]提出雙向更新方案.通過尋找滿足當前更新狀態下其子節點都已更新至新規則,或者在最終狀態下其所有父節點都已經更新至新規則這兩個條件的節點依次更新.但每次最多更新2個節點,更新輪數依然過多.針對依賴問題,Mahajan等[12]提出了最優化更新.方案設定每個節點都具有3個狀態,在保證無環的情況下,讓盡可能多的節點并行更新,從而最大程度減少更新輪次.但此方案每一輪都要全局遍歷以更新節點狀態,節點搜索復雜度高.

1.4 基于分類搜索的無環更新

針對分類時序更新應用場景適用性差和更新時延長、最優化更新計算復雜度高等問題,本文在兩者基礎上,提出基于分類搜索的無環更新一致性方案（Categorical Search based loop-free Consistent Update scheme,CSCU）.在CSCU方案中,我們設計了一種交換機分類模型和一種環路搜索優化模型,其中優化模型包括環路檢測模塊和搜索模塊.兩種模型結合的更新流程可概括為:分類模型先分析所有節點的更新前后狀態并初始化; 再調用環路搜索優化模型的環路檢測模塊獲取對應節點集的可更新節點進行更新.最后,在未更新節點集中循環調用優化模型的搜索模塊查找滿足條件的可更新節點,直至更新完成.

本文的主要貢獻在于:

（1）改進分類時序更新算法中的分類方式,構建了一種新的交換機分類模型,它可以增大應用場景的適用性和減少更新等待時延.

（2）在分類和節點依賴的基礎上,通過分析更新前后轉發規則的差異,構建相應的環路搜索優化模型,優化了更新的搜索計算復雜度和更新效率.

（3）在分類模型和環路搜索優化模型的基礎上,提出一種基于分類搜索的更新方案,它具有更新時延短,更新效率高的優點.

2 SDN系統模型

在本節中,我們通過構建網絡模型和更新模型對整個SDN網絡的更新過程進行分析.

2.1 網絡模型

我們將網絡建模抽象為一個圖G=（N,L）,其中,N是網絡的節點集,L是節點間的鏈路集.為了簡化,本節假設網絡模型為單一控制器C0和多OpenFlow交換機S={s1,…,sn-1}的模式,圖2展示了本節所述的網絡模型.其中,實線是交換機間轉發數據包的數據鏈路,虛線是控制器和OpenFlow交換機間的控制鏈路（也稱OpenFlow通道）.

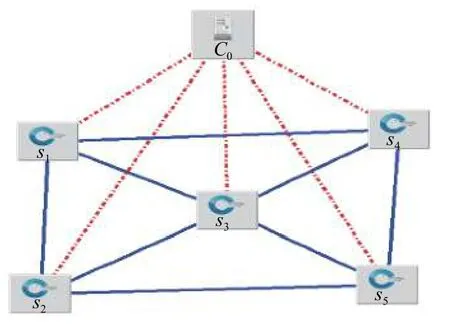
圖2 SDN網絡示意圖

在SDN網絡中,節點集N可用數學表示為:N=C∪S,其中,C是控制器集,S是交換機集.鏈路集L可定義為 L=Lcc∪Lcs∪Lss,其中,Lcc指代控制器與控制器之間的鏈路集,Lcs指代控制器和交換機間的控制鏈路集,Lss指代交換機和交換機間的傳輸鏈路.由于模型簡化為單控制器模式,因此集合Lcc為空,集合Lcs的元素個數為|S|=n-1.

交換機流表規則Ri可定義為一個三元組.其中,Pri指代規則的優先級,Mi指代規則的匹配域集（OpenFlow協議中,流規則使用多個字段來匹配數據包,包括以太網源地址、以太網目的地址、VLAN ID等）,Ai指代規則的動作集.如果進入網絡的數據包同時匹配多條規則,則選擇優先級最高的規則,并執行相應的動作.

2.2 更新模型

網絡更新是對網絡配置的更新操作:SDN控制器生成更新消息并將其轉發給交換機,然后交換機根據此消息改變它的規則表.很明顯,更新前后涉及交換機狀態的變化.因此可將t時刻的交換機狀態定義為[2]:

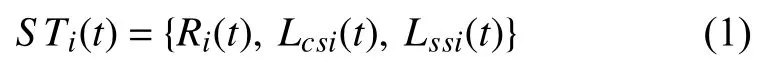
其中,Ri（t）指在t時刻的交換機Si的規則集,Lcsi（t）代表t時刻與Si相關的控制鏈路集,Lssi（t）代表t時刻與Si相關的數據傳輸鏈路集.

網絡配置,即網絡中所有交換機的狀態并集,則t時刻的網絡配置可定義為:

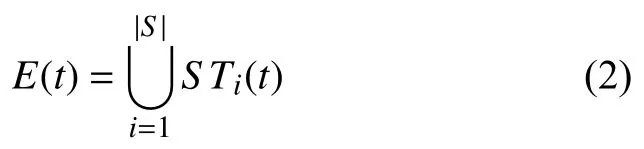
網絡更新是對網絡配置的更新操作,即不同時刻的網絡配置的遷移.因此,網絡更新可定義為:

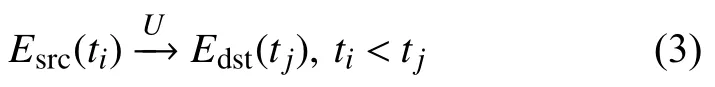
其中,Esrc（ti）代表更新前的網絡配置,Edst（tj）代表更新后的網絡配置,U指代網絡配置遷移過程的更新操作集.

基于OpenFlow協議中流表的組成部分,可以將數據包在交換機中的處理定義為布爾函數:

其中,s代表交換機,p代表數據包; X代表匹配域,Y代表處理結果（包含動作:將數據包轉發到其他交換機或將數據包上傳至控制器）.

數據包從進入網絡到離開網絡,是數據包在交換機間的相互轉發過程.由式（4）可知,數據包在網絡轉發是個迭代處理過程,因此,可將數據包在網絡中的操作以布爾函數的形式定義為網絡轉發函數F（p）:

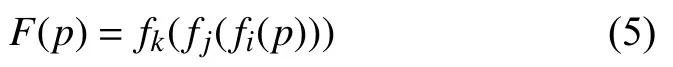
其中,p指代數據包,i,j,k指代交換機編號（假設數據包在網絡中的傳輸路徑為i→j→k,即數據包p先在交換機Si被處理,然后根據定義（4）得到的結果,將數據包轉發到交換機Sj中進行處理,以此類推,直至轉發完成）.

使用πold表示舊數據包,則舊數據包可定義為:如果一個數據包p被尚未更新的交換機處理,那么它就被標記為πold.同理,使用πnew表示新數據包,則可定義為:如果一個數據包被已更新了的交換機處理,它將被標記為πnew.因此可將網絡轉發函數拓展為:

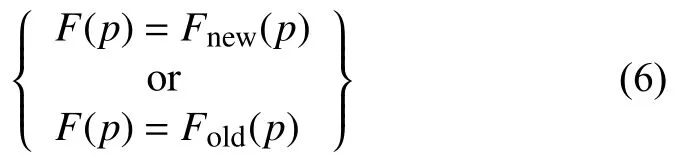
其中,Fnew（p）和Fold（p）代表πnew和πold由新/舊規則集處理.

包一致性.由網絡轉發函數定義可得:每個數據包的傳輸函數應該只涉及一個規則集:F（p）=Fnew（p）或F（p）=Fold（p）,而不能是兩者的混合.

更新持續時間（Ud）.Ud指控制器發送第一個更新消息和最后一個交換機更新完成之間的時間間隔.

更新輪次（Uround）.本節假設在單個交換機上安裝的規則之間沒有沖突或者依賴關系,從而可以在單輪消息傳遞中更新交換機而不影響網絡一致屬性.Uround指更新過程所需的階段更新次數,在一定條件下,Uround直接影響Ud,兩者成正相關.每輪中,控制器更新一個交換機子集,并保證以任何順序更新該子集的交換機都能確保無環路產生.控制器在確認前一輪中選擇的交換機都已經在內存中安裝了新的規則后,再開始新一輪的更新.

節點操作復雜度（Ncp）.指更新過程對交換機流表操作的復雜程度.流表規則更新操作類型和操作次數是Ncp的關鍵影響因素,會直接影響Ud和更新性能.

本節模型構建主要為了優化更新調度算法,提升更新性能.因此,我們可將本模型的優化目標和約束問題描述為:

其中,式（7）為優化目標,即通過最大程度的減少更新輪次Uround和降低節點操作復雜度Ncp來減少更新持續時間Ud.式（8）和式（9）為約束問題,其中,式（8）代表更新過程需保證不會引起轉發環路、式（9）代表更新過程需保持包級一致性.

本模型的難點在于如何設計更新調度算法,在保證更新過程無環路產生、數據包轉發保證一致性的前提下,盡可能的減少更新所需時間,提升更新性能.由于單輪更新不會影響網絡的一致屬性,因此,SDN控制器可協調交換機間的規則更新,通過設計更新算法,使更新輪次最小化,減少完成更新的所需時間.已經證明,最小化更新輪數是NP完全問題[13].

3 基于分類搜索的無環一致性更新方案

3.1 問題描述

定義Pold和Pnew分別代表Esrc（ti）下的數據原始傳輸路徑和Edst（tj）下的數據最終傳輸路徑,nexthop（s,Pold/Pnew）代表節點s在路徑Pold或Pnew的下一跳.更新過程中,配置是否更新成功受設備之間的實時交互時延、設備的實時更新操作所影響,可能會因為上述因素導致網絡中出現環路等問題.基于以上定義,可將方案的問題描述為:已知Esrc（ti）和Edst（tj）,通過分析Pold和Pnew上的節點,在滿足式（8）和式（9）的前提下,設計更新算法,尋找更新輪數較少、更新性能較優的操作集U,求得式（7）的最優解.

3.2 基于分類搜索的更新方案

3.2.1 CSCU方案的節點集合定義

在構建模型過程中,本方案基于分類和節點依賴搜索思想,需要創建和更新以下相關集合,如表1.其中,Pnew[length-1]指代最終傳輸路徑上的最后一個節點、Ssubi代表每一輪更新后剩余的待更新節點集、rmax代表完成整個更新過程所需要的最大更新輪數、check_loop（s,Pold,Pnew）用于判斷更新節點s是否引入環路、judge_allfather（s,Pold,Pnew）用于判斷節點s的父節點是否都已經更新至新規則.

表1 相關節點集

3.2.2 CSCU方案的流程

先給出節點依賴關系的定義:當節點Na必須在節點Nb更新完成之后才能更新,則節點Na依賴于節點Nb.另外,由于目的節點不涉及規則更新,定義為不需要更新節點.CSCU方案的更新流程如圖3所示.

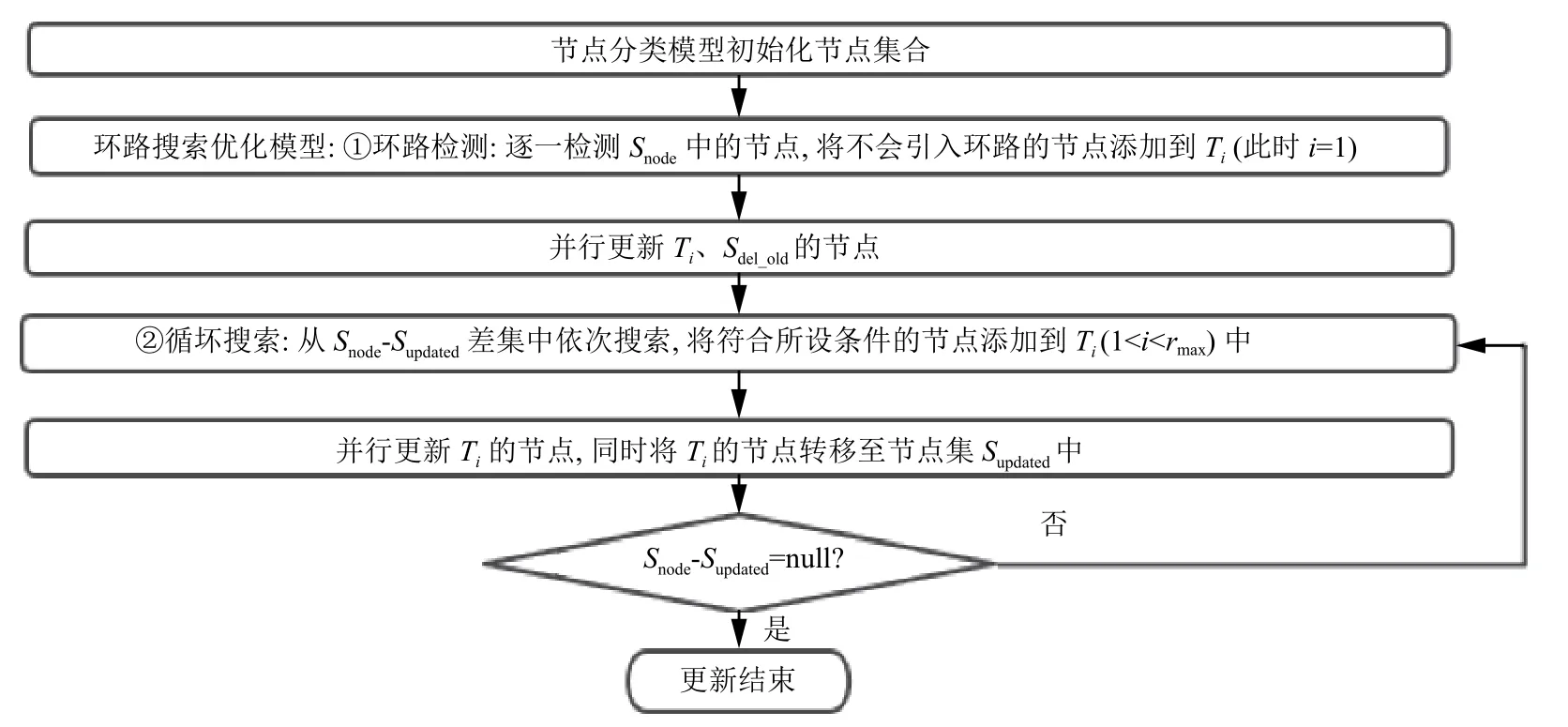
圖3 CSCU更新流程

首先,CSCU方案利用節點分類模型對Esrc（ti）和Edst（tj）進行分析,通過對比Pold和Pnew節點狀態,初始化表1中的節點集.

分類模型初始化后,執行環路搜索優化模型中的第一個模塊.調用基于拓撲排序算法的環路檢測模塊逐一檢測Snode中的全部節點—直接給節點增添新的轉發規則.如果check_loop（Ni,Pold,Pnew）=True,即不會引入環路,則將Ni添加到節點集Ti中（此時i=1）.檢測完畢后,并行更新節點集Ti和Sdel_old中的節點.其中,對Ti中的節點實施以下操作:下發新規則替換舊規則,同時將節點轉移至節點集Supdated中.對于Sdel_old中的節點,直接刪除對應的舊規則后,移除該節點.舊規則是否刪除,同樣是判斷一個節點是否已經更新的依據.Sdel_old存儲只需刪除舊規則的節點,由于節點規則失效時間不確定,如果沒有及時刪除Sdel_old中節點的舊規則,會影響方案接下來根據依賴關系搜索可更新節點的算法.當以上節點集更新完成,算法繼續.

接著,調用環路搜索優化模型中的第二個模塊.對Ni∈Snode?Supdated依次搜索可更新節點,將滿足條件Find_father（Ni）=null或judge_allfather（Ni,Pold,Pnew）=True的節點Ni加入Ti中,前面兩個條件表示當前狀態下的節點Ni無父節點或者父節點都已更新.搜索完后,并行更新Ti的節點,同時將Ti的節點轉移至Supdated中.如果Snode?Supdated≠null,則循環執行搜索.直至Snode?Supdated=null,方案結束.

后文我們將證明,結合分類模型和環路搜索優化模型雙模型,CSCU方案能有效提高更新效率,且具有更低的計算復雜度.

3.2.3 CSCU方案的更新示例

現以圖4所示拓撲為例,將網絡抽象為一個點對點有向圖來演示CSCU方案的更新過程.其中,實線代表網絡配置更新前數據轉發路徑,虛線代表更新后數據轉發路徑.更新步驟如圖4所示.

圖4 更新例子

（1）執行節點分類模型初始化集合得:Snode={N1,N2,N3,N4,N6,N7,N9,N11},Sdel_old={N5},Sun={N8,N10},Supdated=null,Ti=null.

（2）調用環路搜索優化模型的環路檢測模塊檢測得:T1={N1,N2,N4,N6,N11}.并行更新節點集Sdel_old和T1中的節點,對s∈T1執行新舊規則替換并將s轉移至Supdated中.對s∈Sdel_old執行刪除舊規則操作,并移除節點s.此時得到Supdated={N1,N2,N4,N6,N11},Sdel_old=null.

（3）然后,調用搜索模塊從Snode-Supdated依次搜索符合條件的節點得T2={N3,N7},執行更新后,此時得到Supdated={N1,N2,N3,N4,N6,N7,N11}.

（4）循環搜索得T3={N9},執行更新后得Snode={N1,N2,N3,N4,N6,N7,N9,N11}.很明顯,此時Snode-Supdated=null且Sdel_old=null,更新完畢.

3.2.4 與其他方案對比

以圖4為例將CSCU方案與其他方案做比較:

（1）基于分類時序更新[7]:① 控制器將交換機初始化,分成4類:入口交換機、新路徑交換機、舊路徑交換機、出口交換機.② 更新出口交換機{N10}和新路徑交換機Snew={N1,N3,N2,N4,N11,N8,N9,N7,N6},執行插入待新增流表項操作.③ 等待一個最長端到端時延后,更新入口交換機{N1},執行修改流表項操作.④ 等待最長端到端時延,更新舊路徑交換機Sold={N1,N2,N3,N4,N5,N6,N7,N8,N9}和出口交換機{N10},執行刪除流表項操作,全部更新完畢.顯然,在新舊規則所涉及的交換機存在復雜關聯時,方案需要在不同階段對大量共同交換機、不需更新的交換機進行不同的流表操作,增加了交換機更新操作次數,這會增加更新的等待時延.

（2）反向更新[6]:該方案所有的節點嚴格依據新規則從目的節點遞歸向前更新.由于默認目的節點不需更新,因此,所需的更新輪次=新規則涉及的節點數-1.由圖4示例可知,新規則轉發路徑涉及的節點數為10,即需要9輪才能完成更新.

（3）雙向更新[11]:依據兩個搜索條件得到{（N1,N6）→（N2,N7）→（N3,N9）→（N4,N8）→（N5,N11）},共需要5輪才能完成更新.

（4）最優化更新[12]:依次加入新規則對所有節點進行無環檢測,找到的依賴森林根節點有{N1,N2,N4,N5,N6,N11},分別刪除其舊規則,再通過無環檢測尋找其子節點,得到依賴樹有:N2→N3,N6→N7→N9,故整個依賴森林為{N1,N2→N3,N4,N5,N6→N7→N9,N11}.其中,依賴森林中依賴樹的最大高度為所需更新輪次,即完成更新共需要3輪.

本文提出的CSCU方案:執行分類模型后,通過執行環路搜索優化模型的無環檢測模塊,得到的T1={N1,N2,N4,N6,N11},再循環執行搜索模塊獲得T2={N3,N7},T3={N9}.所以,經過3輪即可完成更新.

3.3 CSCU無環性驗證

無環性是方案的主要研究點,證明如下:

（1）首先,環路搜索優化模型中的無環檢測模塊不會引入環路.事實上,在更新過程中,基于拓撲排序的無環檢測模塊對節點集Snode中的節點進行檢測,是根據直接增加新規則是否會產生環路來決定.若產生環路則保持狀態不變,否則就將它逐一添加進節點集Ti中.然后并行更新Ti和Sdel_old中的節點:對s∈T1執行新舊規則替換并加入Supdated中,對s∈Sdel_old執行舊規則刪除.因為節點只有通過無環檢測才確定是否更新,并行更新Ti中的節點的過程顯然不會引入環路.另外,對s∈Sdel_old執行刪除舊規則的操作,只是釋放相應的交換機內存空間,不會引起無環.所以,無環檢測更新過程不會引入環路.

（2）其次,環路搜索優化模型中的循環搜索模塊也不會引入環路.事實上,按默認方法更新至最終狀態的路徑是不存在環路的.現假設當前狀態下有局部鏈路N1→N2→Ncur,Ncur尚未更新,其父節點N1,N2都已更新.更新Ncur,形成環路Ncur→N1→N2→Ncur,而根據假設,其父節點都已更新,即整個環路鏈路涉及的節點都已更新至新規則.該環路是整個更新至最終狀態的一個局部鏈路,則與最終狀態下的新規則中無環路的矛盾,所以更新Ncur不會引入環路.循環搜索更新,直至Snode-Supdated=null時更新完畢,整個更新過程都不會出現環路.

3.4 相關研究比較

本節將從適用性、更新持續時間Ud、更新節點操作復雜度Ncp、更新算法計算復雜度4個方面進行比較.適用性,指方案場景適用范圍.Ud為整個更新過程每個階段所用時間總和,集中體現于更新過程的所需輪次Uround,更新所需輪次越多,等待更新的時間越長,Ud越大.Ncp指更新過程對節點操作的復雜程度,集中體現于:需在不同更新階段執行不同更新操作的節點越多、對同一節點更新操作的次數越多,更新等待時延就越長,Ud越大.更新算法計算復雜度,指切換更新規則過程中相應邏輯功能計算的復雜性.

本節將本文方案與第2節的相關研究進行比較,結果如表2所示.

表2 本文與相關方案比較

（1）適用性.不管網絡拓撲復雜與否,分類時序更新都依據新舊轉發路徑上的節點嚴格設定階段進行更新.若網絡配置簡單,使用該方案反而降低更新效率.若配置更新存在大量的共同交換機,則需要分別在不同的更新階段,對同一交換機進行不同的流表操作,更新操作量增加.因此,分類時序存在一定的應用場景局限性,適用性較差.本方案在分類初始化基礎上,設計能減少更新輪數的環路搜索優化模型,無論拓撲結構復雜與否,本方案更新效率都有保證.

（2）更新持續時間Ud.分類時序更新設定固定階段更新,下一個階段的節點更新必須等待上一個階段的節點更新完畢才能進行,更新輪次固定.若更新配置復雜,還會因為等待舊包流出網絡等待端到端的最長時延,增加更新時間.反向更新和雙向更新節點依賴復雜,導致更新輪次多,更新時延高.本方案結合分類模型和環路搜索優化模型,平均更新輪次接近最優化更新,更新持續時間短.

（3）更新節點操作復雜度Ncp.如3.2.4節所述,更新配置復雜時,分類時序更新需在不同階段對大量節點進行不同的流表更新操作,大量節點更新操作次數多.因此,方案的更新節點操作復雜程度高,更新等待的時延長.雖說細化流表項操作在更新某一階段能使新舊數據包并行傳輸,一定程度上降低控制器負載.但與其產生的等待時延相比,時間開銷更為重要.本方案只需針對相應節點集執行相應規則操作,操作復雜度低,等待時延少,能進一步減少Ud.

（4）算法計算復雜度.假設使用鄰接矩陣存儲節點信息.最優化更新中,初始化所有節點狀態、加入新規則檢測是否引入環路都為O（n）,在狀態轉換過程中,更新節點狀態和下一輪節點的判環操作也都為O（n）.因此,最優化更新的時間復雜度為O（n4）.CSCU方案中,分類初始化和對待更新的節點判環操作的總時間復雜度為O（n2）,搜索可更新的節點為O（n）,因此總的時間復雜度為O（n3）.而基于分類時序更新只需遍歷矩陣進行分類,然后在不同節點進行更新,時間復雜度為O（n2）.

4 仿真分析

為了分析比較相關方案在不同情況下更新的效果,本文基于自主搭建的SDN仿真平臺進行模擬實驗.平臺所用設備為Ubuntu 16.04操作系統,RYU開源控制器和mininet網絡仿真器.仿真實驗設定實驗拓撲節點數,設定源點和目的節點.每次實驗通過隨機更改相鄰節點的邊權值來模擬網絡拓撲結構的變化,相鄰節點的邊權值服從（1-1000）的均勻分布.權值確定后,再通過OSPF算法獲取源節點到目的節點的路徑.

① 關于更新輪次和更新持續時間Ud的關系,在上一節已經有詳細解釋.在此,通過300次仿真實驗測試,對相關研究方案每一次實驗的更新輪次進行分析對比,結果如圖5所示.

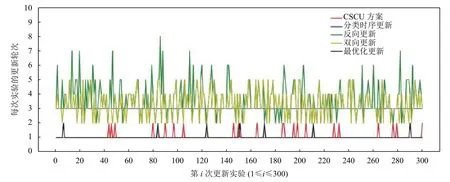
圖5 不同方案下的更新輪次情況

實驗結果顯示,反向更新的所需的更新輪次普遍多于其它方案,這是因為反向更新只與新的轉發規則相關,更新輪次=新規則轉發相關節點-1.由于分類時序更新嚴格設計更新階段,因此更新輪次固定.本方案的更新輪次接近最優化更新,比其他方案都少.

② 配置更新交叉程度.指配置更新過程中,同時在新、舊路徑上的交換機占與更新相關的交換機總數的比例.配置更新交叉程度的大小影響CSCU方案的更新性能.更新過程中,在新路徑上而不在舊路徑上的交換機數越多,涉及舊規則的交換機就越少,就越難形成回路.因此,更新輪次就越少,更新性能越好.相反則需要更多的輪數來完成更新.

至此,就配置更新交叉程度對本方案更新輪次的影響進行實驗分析.由于交叉程度低的時候形成環路的可能性低,所以交叉程度為0和25%的結果參考價值不大.因此本實驗只對交叉程度為50%、75%、100%的情況進行實驗,結果如圖6所示.

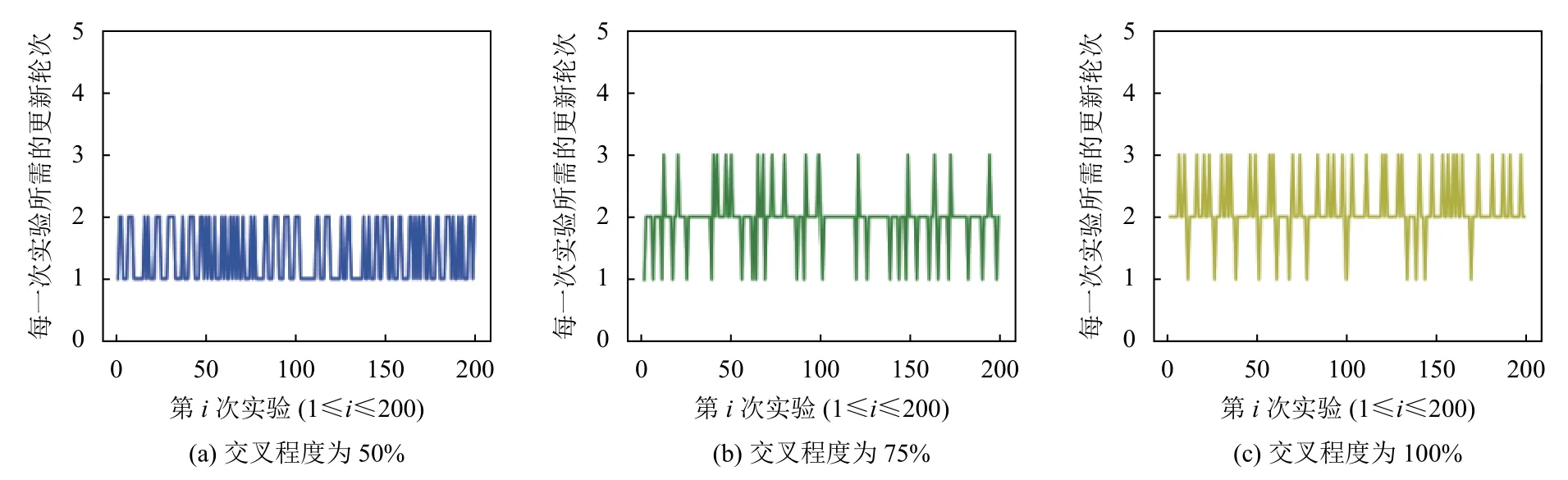
圖6 CSCU方案在不同配置交叉程度下的更新輪次情況

為了更好的與分類時序更新對比分析,綜合CSCU方案在不同交叉程度更新情況的實驗結果,求得配置更新不同交叉程度下的平均更新輪次.實驗結果表明,本方案在配置更新交叉程度為0、50%、75%、100%下的平均更新輪次都比分類時序更新少,結果如圖7所示,其中,0、50%、75%、100%分別代表CSCU方案的配置更新交叉程度,timing代表分類時序更新.

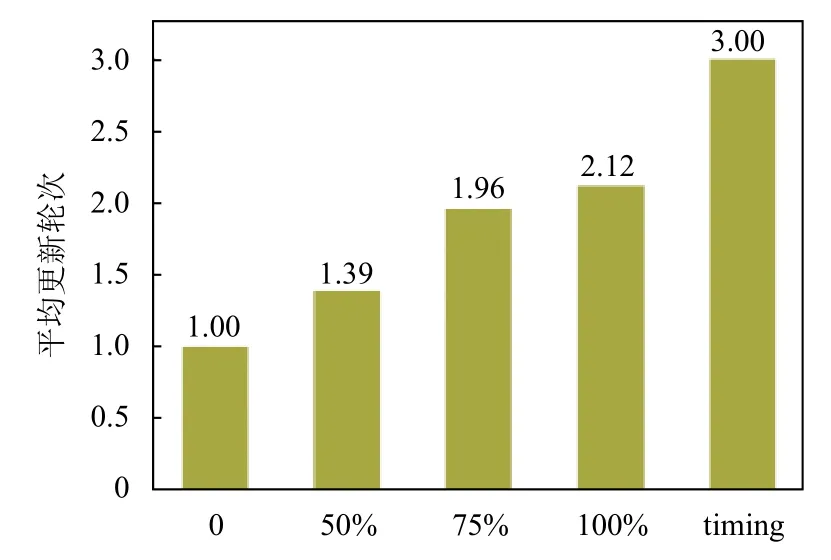
圖7 不同交叉程度下與分類時序更新的比較

③ 更新過程的節點操作復雜度直接體現于對同一交換機的流表項操作次數大于1的交換機數.用num_large_1表示對同一交換機的流表項操作次數大于1的交換機數.顯然num_large_1越大,更新的節點總操作次數越多,更新過程的節點操作復雜度就越高.針對節點操作復雜度,本節設計多次實驗,假設實驗的節點數固定為20、新舊路徑跳數相同.對分類時序更新進行測試分析,得出num_large_1的平均值隨路徑跳數變化的情況,實驗結果如圖8所示.實驗設定新舊路徑源、目的節點,所以num_large_1≥2.

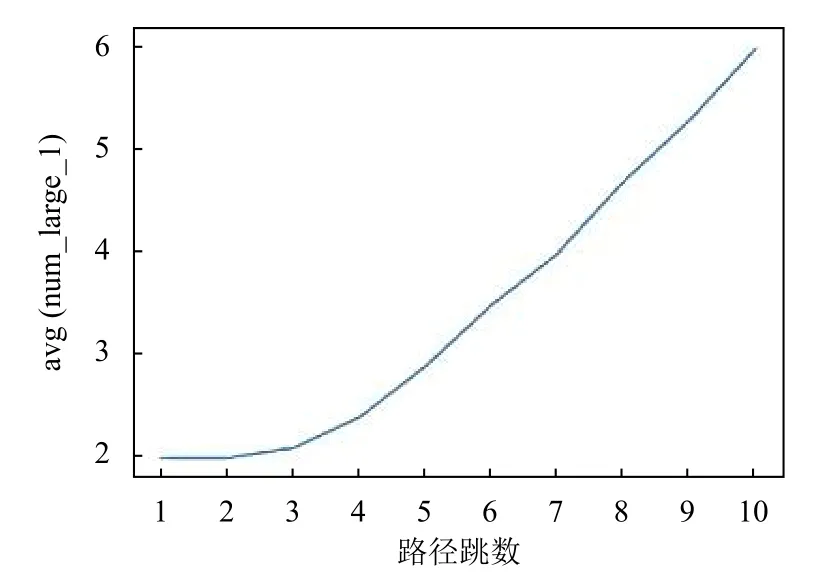
圖8 不同路徑跳數的更新節點操作復雜度

分析實驗可得,網絡節點數一定的情況下,num_large_1隨著路徑跳數的增大而增大.即隨著路徑跳數的增多,同是新舊路徑上的節點的節點數就越多,對所有節點的總操作次數就越多.因此,更新過程的節點操作復雜度就越高.而本方案經分類初始化后,與更新配置復雜度無關,更新節點操作復雜度低.

綜上所述,相較于分類時序更新,基于分類搜索的無環更新一致性方案有更好的場景適用性、更低的節點操作復雜度Ncp和更少的更新輪次Uround,能夠在滿足模型約束條件（8）和（9）的前提下有效減少更新持續時間Ud、提升更新效率,實現模型的優化目標.另外,在更新輪次方面,本方案相對于其他相關研究方案都有著不同方面的性能提升.

5 結語

本文根據在研項目的研究目標,對SDN流表更新一致性的相關研究成果進行了詳細的研究.并針對基于分類時序更新方案存在應用場景適用性差、更新時延長和節點更新復雜程度高等問題,提出了一種基于分類搜索的無環更新方案.隨后,本文通過更新示例的展示,在適用性、更新時間等性能方面對該方案和相關研究方案進行了對比分析.此外,本文對該方案的無環一致性更新進行了理論分析,證明了方案的可行性.最后,通過搭建SDN仿真平臺進行了仿真實驗.仿真實驗針對更新輪次對該方案與相關研究方案進行了分析對比,也針對不同配置更新交叉程度和節點操作復雜度單獨跟分類時序方案進行了對比.仿真結果表明,CSCU方案具備應用場景適用性高、節點更新操作復雜度低的優點,是一種能夠有效的減少更新所需輪次、更新時延和降低計算時間復雜度的高效率更新方案.