基于APIT的無線傳感器網絡混合定位算法①

李云鵬

（沈陽工業大學 信息科學與工程學院,沈陽 110870）

1 引言

無線傳感器網絡定位算法根據其定位原理可以分為兩類[1]:基于測距的（range-based）定位算法和非基于測距的（range-free）定位算法.基于測距的定位算法,先通過測距技術獲得節點之間的距離或角度信息,再使用三邊測量法、三角測量法或最大似然估計法等估算節點位置,主要算法有TOA[2],TDOA[3],AOA[4]以及RSSI算法[5].非基于測距的算法則無需測量節點間距離和角度等信息,而是利用節點間連通度及鄰居關系實現定位,主要算法有Centroid算法[6]、DV-HOP算法[7]、Amorphous算法[8]以及APIT算法[9].

2 APIT算法

基于測距的算法雖然可以取得精度較高的定位結果,但該類算法對節點硬件要求較高,并且需要產生大量的計算和通信開銷,不適合大規模應用.非基于測距的算法在成本、功耗等方面具有明顯優勢,對硬件要求也不高,精度足夠滿足大部分應用場景,性價比較高.相對于其他非基于測距的算法,APIT算法具有較高的定位精度,以及通信開銷小等優點,具有很強的適用性.

2.1 APIT算法原理

APIT算法原理如圖1所示,未知節點從它的通訊范圍內所有的錨節點中任意選擇3個組成三角形,通過與其他錨節進行節點信息交換對比來測試該未知節點是否在三角形中,重復此測試直到窮盡所有可取的三角形組合,計算包含未知節點的所有三角形的重疊區域,將重疊區域的質心作為未知節點的估計位置[9].

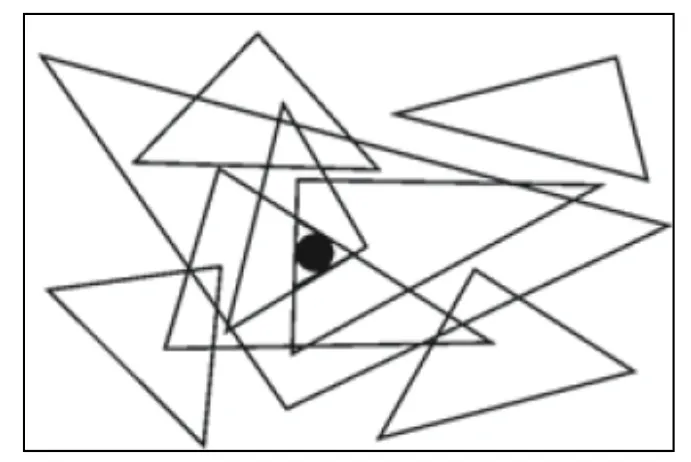
圖1 APIT算法原理圖

APIT算法在尋找重疊區域時采用網格掃描法[10],即將定位區域平均分割成正方形網格并給每個網格一個計數器,若未知節點在三角形內部,則三角形掃到的網格的計數器加1,反之則減1,最終將計數器數值最大的區域的質心作為未知節點的估計位置.

2.2 APIT算法不足及分析

一方面,APIT算法雖然與其他非基于測距的算法相比定位精度較高,但仍有較大提高空間; 另一方面,APIT算法相比其他算法有著相對低覆蓋率,這也是APIT算法另一個研究重點.

APIT算法定位精度的不足,主要源于在網格掃描法.在網格掃描法中被三角形掃描到的區域無論大小,都同樣計數器加1,致使一大一小區域對結果的影響相同.此外,未知節點在三角形外時,存在被誤判在三角形內的可能[11],從而使估計位置產生較大偏差,定位精度下降.

APIT算法定位覆蓋率的不足,主要源于其算法本身.APIT算法需要未知節點通訊范圍內存在3個及以上錨節點才能進行定位,然而在隨機分布的傳感器網絡中,錨節點可能在局部密度不足,致使未知節點通訊范圍內錨節點不足3個,從而無法進行定位,最終導致定位覆蓋率不足[12].

3 APIT與遺傳算法混合定位

由于上述兩點問題的存在,造成了APIT算法定位精度與定位覆蓋率的不足,為克服此問題,本文提出了一種APIT算法與遺傳算法混合定位算法.

3.1 三角形比較分割

針對APIT算法定位精度不足的問題,本算法在經典APIT算法的網格掃描法部分,引入三角形比較分割[13]以提高精度.在△ABC內,并且邊BC>AC>AB,過A點作BC垂線于D,即可知∠CDP的大小,若∠CDP小于90°,則未知節點在△ACD內,反之,則在△ABD內,如圖2所示.

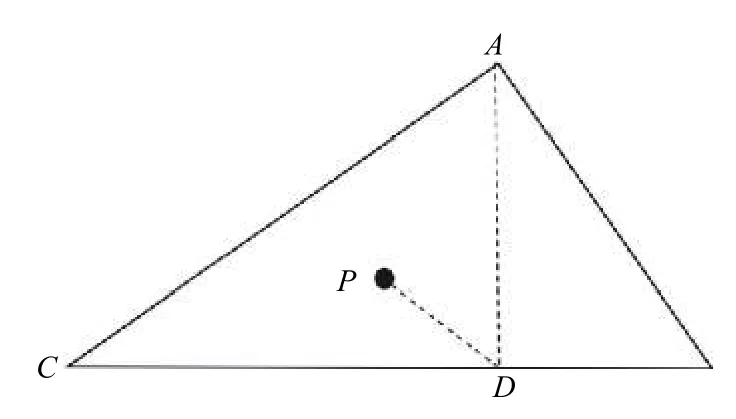
圖2 三角形比較分割原理圖

多次應用此判斷,并將所在三角形最長與網格邊長比較,直至最長邊長度小于網格邊長,比較分割結束,具體過程如下:

（1）通過點A、B、C坐標計算出點D坐標;

（2）通過RSSI計算出AP、BP、CP長度;

（3）利用余弦定理與距離公式可計算:

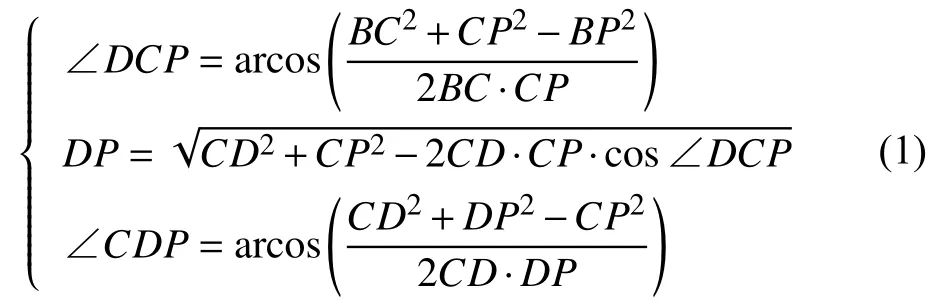
（4）若∠CDP小于90°,則未知節點在△ACD內,反之,則在△ABD內.

（5）將未知節點所在三角形邊長進行排序,令最長邊為BC,最短邊為AB,第三邊為AC.若BC大于網格邊長,重復步驟（1）-（4）,反之,則結束分割.

3.2 遺傳算法定位

遺傳算法[14]是一種借鑒生物界自然選擇和自然遺傳機制的隨機搜索算法.作為一種優化算法,遺傳算法不依賴于梯度信息,而是通過模擬自然進化過程來搜索最優解,具有很好的全局搜優特性.遺傳算法不僅可拓展性高,便于與其他算法組合優化,在數學上也易于實現,其目標函數的定義域可以為任意集合且不會受到連續可微的約束,這種特點使得遺傳算法非常適合求解定位問題[15].

針對APIT算法定位覆蓋率不足的問題,本算法引入遺傳算法對未知節點進行定位[12],即當未知節點通訊范圍內錨節點個數為2時,在以兩個錨節點為圓心,以通訊范圍為半徑作圓,在兩圓相交處用遺傳算法求解未知節點,確定目標函數,使未知節點到錨節點的真實距離與測量距離的絕對誤差最小,將未知節點的求解轉換為求解有約束條件的二元二次方程.

其中,δ為設定的誤差閾值,其原理如圖3所示.

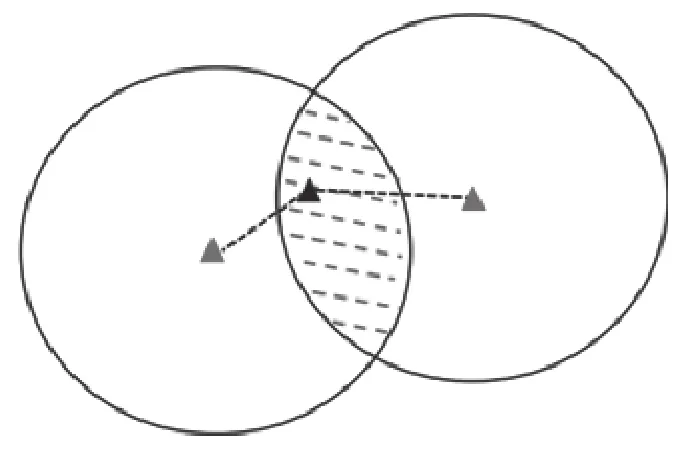
圖3 遺傳算法定位原理圖

遺傳算法定位具體過程如下:

（1）在兩圓相交的陰影區域內隨機采集N個樣本作為初始種群,N個樣本的平均坐標作為初始位置,根據適應度函數Fi確定每個樣本 Ai的適應度,并記錄最優個體.

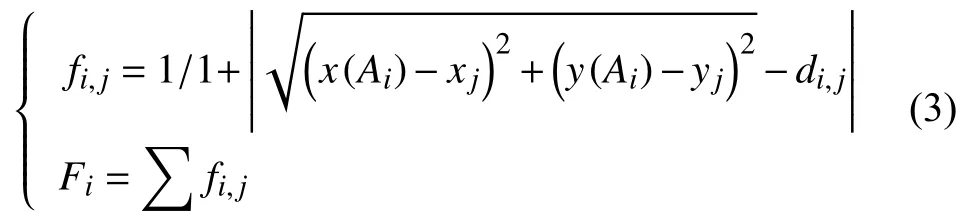
（2）將初始種群中任意一個個體替換為最優個體,再兩兩隨機配對,按照一定概率進行交叉操作產生新的個體.其中,隨機數α∈（0,1）.

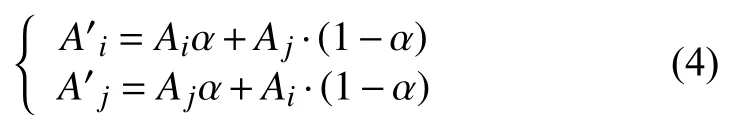
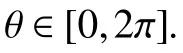
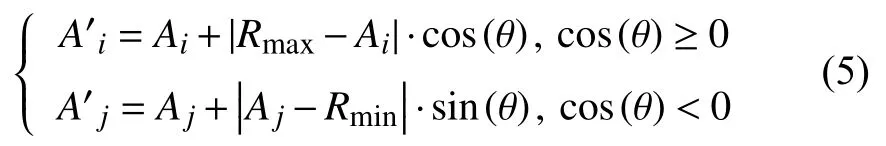
（4）若達到預設最大迭代次數,則輸出最優解并結束,否則轉到步驟（2）.

本文最大迭代次數設置為40.

4 仿真及分析

4.1 實驗環境及參數設置

本次實驗使用Matlab 2016b對算法進行仿真.在1000 m×1000 m的正方形區域內,隨機分布300個節點,其中60個為錨節點,240個為盲節點,節點通訊距離為200 m,由此組成一個無線傳感器網絡進行定位仿真.遺傳算法部分,初始種群為400個,交叉概率為0.9,變異概率為0.02.

4.2 實驗結果及分析

圖4為本文算法在上述仿真環境下,實驗結果與迭代次數的關系.

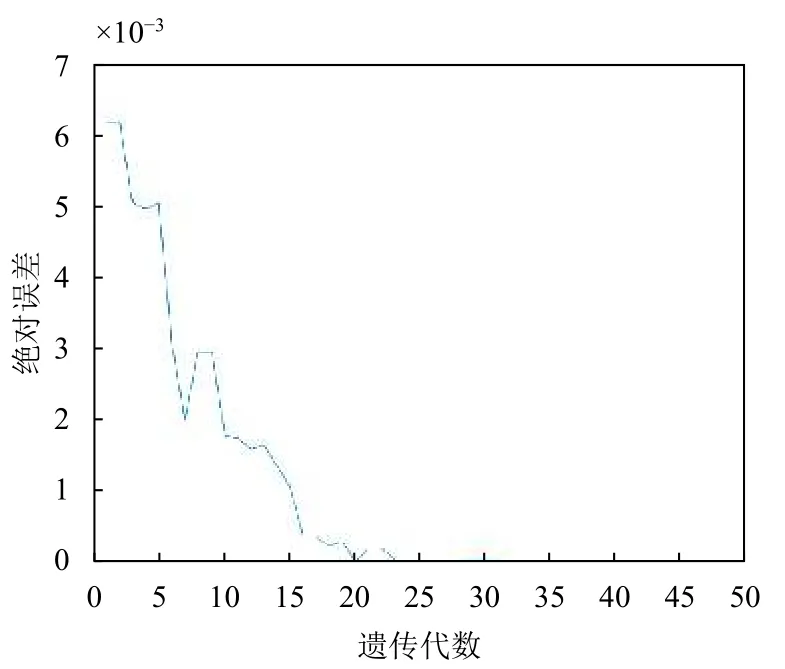
圖4 實驗結果與迭代次數關系圖

由圖4可知,本文算法在迭代40次后,實驗誤差逐漸趨近于0,達到理想狀態,以此確定遺傳算法結束條件為最大迭代次數40次,并將此條件應用于后續仿真.

圖5、圖6分別為經典APIT算法與本文算法節點分布圖.其中,紅色*表示錨節點的位置,藍色○表示未知節點的實際位置.分布圖將未知節點的實際位置與估計位置用線段相連,用線段的長短來體現未知節點的定位誤差,沒有用線段連接的黑色○為無法定位的節點.

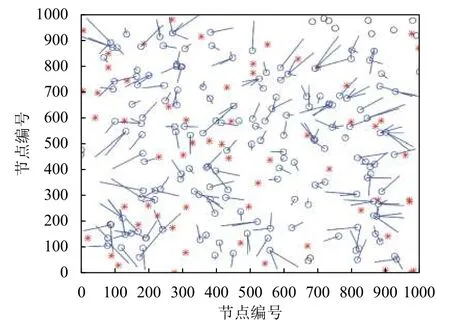
圖5 APIT算法定位節點分布圖

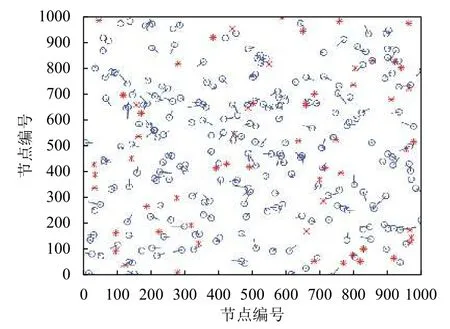
圖6 本文算法定位節點分布圖

圖7、圖8分別為經典APIT算法與本文算法仿真的誤差結果圖.在實驗中,未知節點實際位置與估計位置的歐氏距離與通訊半徑的比值被定義為誤差,無法定位的節點數量與未知節點總數量的比值被定義為盲點率.

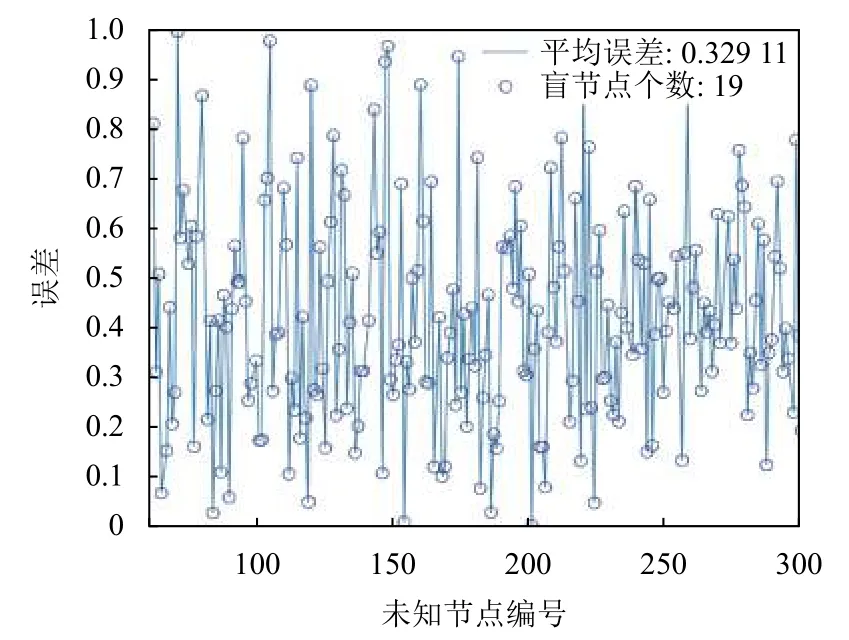
圖7 APIT算法定位誤差圖

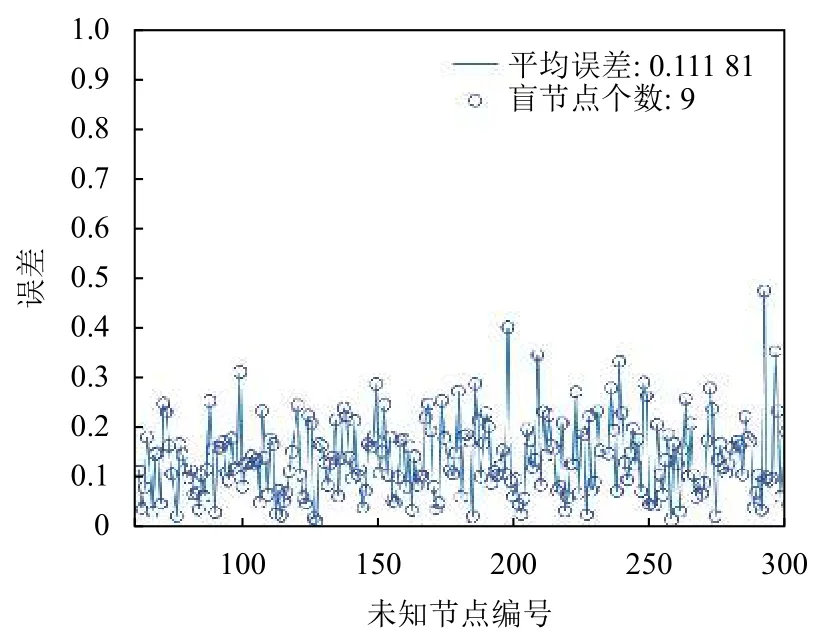
圖8 本文算法定位誤差圖

將兩種算法分別仿真100次,取平均值作為算法結果,經典APIT算法的誤差為32.41%,盲點率為7.24%;本文提出的混合算法誤差為10.79%,盲點率2.37%.結果表明,本文提出的混合算法相較于經典APIT算法定位精度提高21.62%,覆蓋率提高4.87%.

文獻[16]提出了一種基于改進差分進化的定位算法,即DEDV-Hop定位算法,文獻[9]提出了一種基于虛擬節點的定位算法,即EVN-APIT定位算法.圖9、圖10分別為在100 m×100 m區域內,總節點個數為100個,錨節點個數從5提升至40時,幾種算法的誤差對比圖與覆蓋率對比圖,對比結果顯示,本算法相較于所比較算法均有不同程度優勢.

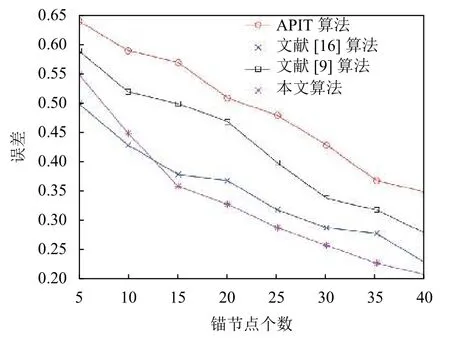
圖9 定位誤差對比圖

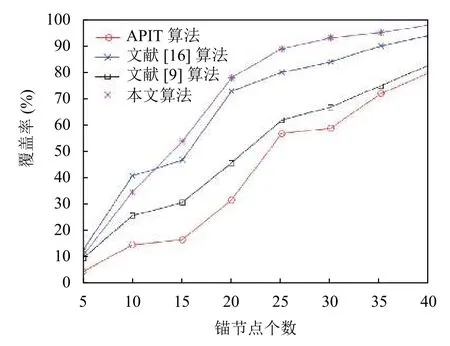
圖10 定位覆蓋率對比圖

5 結論與展望

本文提出一種基于APIT的無線傳感器網絡混合定位算法.算法分為兩個部分:當盲節點通訊范圍內錨節點數量大于等于3個時,通過用比較分割法優化過的APIT算法定位; 當盲節點通訊范圍內錨節點數量等于2個時,通過遺傳算法進行定位.仿真實驗結果驗證了算法的可行性與有效性,本文算法相較于APIT算法在定位精度與覆蓋率上均有不同程度提高.