基于無跡粒子濾波算法的航空發動機排氣溫度預測

余 臻 ，劉 洋 ，魏 芳 ，劉利軍 ，

（1.廈門大學航空航天學院，福建廈門 361005；2.中國航發商用航空發動機有限責任公司，上海 200241；3.中國船舶航海保障技術重點實驗室，天津 300450）

0 引言

航空發動機的工作環境惡劣，多為高溫、高腐蝕、高轉速條件，其安全工作壽命難以準確得知[1]。發動機性能指標包括排氣溫度裕度（Exhaust Gas Temperature Margin，EGTM）、高壓壓氣機轉子角速度偏差量（Delta N2，DN2）、平均滑油消耗率（Average Oil Consumption，AOC）等，其中EGTM 是最重要的指標之一，是發動機在海平面壓力、拐點溫度條件下全功率起飛時，排氣溫度與標準規定的排氣溫度紅線值之間的差值。隨著發動機飛行循環數的增加，發動機各零部件磨損老化程度增加，排氣溫度持續升高，使得EGTM值逐漸降低，達到標準規定的EGTM閾值。

在20世紀90年代初建立的基于發動機性能參數的性能衰退失效分析方法，為高可靠性設備的可靠性分析提供了新的分析方法。Gertsbackh 等[2]率先提出基于性能退化數據的設備可靠性模型的預測方法；Nelson[3]發現發動機部件的失效特性會在發動機衰退信息中有所體現，這些信息能具體反映出零部件的衰退狀態；Meeker 等[4]利用退化失效模型解決了傳統可靠性理論無法很好處理的一些實際問題；Wu 等[5]基于數據驅動的退化量統計模型，采用模糊聚類方法研究了零部件退化失效分布。隨著發動機制造技術的進步，發動機可靠度提高，發動機失效數據大大減少，使得樣本數量減少。Erto[6]利用發動機零部件常見的先驗信息，分別對經典的概率分布模型進行分析，對參數進行了估計；Cox[7]給出了針對單系統的剩余壽命分布的混合估計方法；王鑫等[8]提出了LSTM 預測模型參數優選算法，提高了對故障時間序列預測的準確度；張營等[9]在過程神經網絡的基礎上提出了優化算法，結合混沌粒子群算法對發動機的排氣溫度進行預測，獲得較高的預測精度。

發動機的性能衰退主要表現為其性能衰退參數值呈非線性減小趨勢[10-11]，可采用能夠處理非線性時間序列的方法進行預測。

本文提出了一種基于粒子濾波[12-14]（Particle Filter，PF）的航空發動機剩余大修壽命預測方法。提出的無跡粒子濾波（Unscented Particle Filter，UPF）算法首次應用在航空發動機EGTM 預測領域，UPF 以無跡卡爾曼濾波（Unscented Kalman Filter，UKF）的結果作為建議分布[15]，引入最新觀測值進行預測修正。

1 無跡粒子濾波算法

粒子濾波基于蒙特卡羅和遞歸貝葉斯濾波方法[16]。為了解決粒子權重差異大的問題，有2 種策略，即重采樣和選擇合理的建議分布[17]。重采樣會導致粒子貧化，選擇合理的建議分布是解決退化問題的較優選擇。

粒子濾波是由表示未知狀態空間的采樣值的1組粒子的近似。目前，粒子濾波已經成為了解決非線性、非高斯系統參數估計和狀態濾波問題的主流方法。

1.1 粒子濾波框架

對于航空發動機EGTM 預測，可以用如下的數學狀態空間方程來表示。

系統狀態方程

系統觀測方程

式中：xt∈Rn，為系統的狀態變量；yt∈Rnz，為系統在t時刻的測量值；ft為通過上一時刻的狀態值預測下一時刻狀態值的函數；ht為通過當前時刻狀態值預測輸出值的函數；mt、nt分別為系統的過程噪聲和觀測噪聲，二者之間相互獨立。

貝葉斯濾波包含預測和更新2 部分。預測部分是利用系統的狀態方程，在系統測量值未知的前提下，預測狀態的先驗概率密度

而更新部分則是在已經得到最新的觀測值yt的條件下，對先驗的概率分布進行修正，得到xt的后驗概率

對于一般高階非線性、非高斯過程，式（4）難以求解。所以粒子濾波采用蒙特卡洛采樣來避免積分難的問題。利用一系列從已知分布采樣的粒子來估計后驗概率

式中：δ()為狄拉克函數；N為粒子個數；i為粒子序號。在得到后驗概率后，當前時刻的后驗期望值為。

然而，因為無法獲知真實的狀態后驗概率，所以如果需要通過后驗概率來獲取粒子分布，則需要從1個已知分布q(x|y)中采樣得到粒子

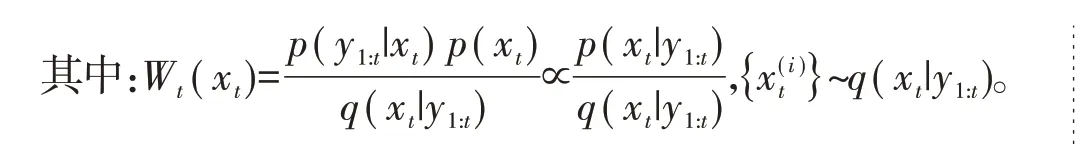
上述粒子權重的計算采用直接計算方式，每進行1 次迭代就需要重新計算，效率低。所以需要重新對權重公式進行遞推

至此描述了完整的粒子濾波算法。從上述算法得知，建議分布q(xt|y1:t)的選取對于算法的效果非常重要。上述涉及到建議分布的內容主要包含2 部分：一部分是粒子是從建議分布中選取的，另一部分是粒子的權重計算需要用到建議分布。同時可知，當建議分布選取為系統先驗分布p(xt|xt-1)時，權重的計算復雜度會大幅降低，即為

這極大地促進了粒子濾波的實際應用。但粒子濾波在易于實現的同時也會導致其他后果：（1）導致了更高階的蒙特卡洛協方差，進而使預測效果變差；（2）使用先驗概率作為建議分布之后，忽略了最新的系統觀測值，可能導致粒子嚴重退化，即大多數粒子的權值都趨近于0，尤其是在似然函數達到峰值而預測的狀態卻在似然函數的邊緣時。建議分布的取值在理論上有無窮多種可能性，但是最優的分布-權值的方差最小，即使存在，求解也十分困難。因此，選擇1 個合理的建議分布，對于避免粒子退化、得到良好的濾波結果具有深刻意義。

1.2 無跡粒子濾波算法

上文已經指出了使用先驗概率作為建議分布會導致系統缺陷，而改進建議分布最明顯的方法是納入當前觀測的數據。于是學者設計出很多的卡爾曼濾波器來改進建議分布[18]，但是這些濾波器的表現多基于各自不同的近似假設。迄今為止，無跡卡爾曼濾波器是針對非線性系統表現最為優秀的卡爾曼濾波器。通過采用無跡卡爾曼濾波器產生合適的建議分布，可以將通用粒子濾波轉化成高性能無跡粒子濾波。下文將討論無跡卡爾曼濾波的基礎——無跡變換，并且給出完整的無跡粒子濾波算法。

在許多現實應用中，都需要估計經過非線性變換y=g(x)的隨機變量的低階統計量，例如均值和協方差。無跡變換能夠準確地計算出g(x)的泰勒級數展開不超過2階的均值和方差。

假定n為系統變量x的維度，x的均值為，方差為Px，則通過無跡變換計算得到y=g(x)的均值和方差。

（1）確定2n+1個sigma點Si={Xi,Wi}。

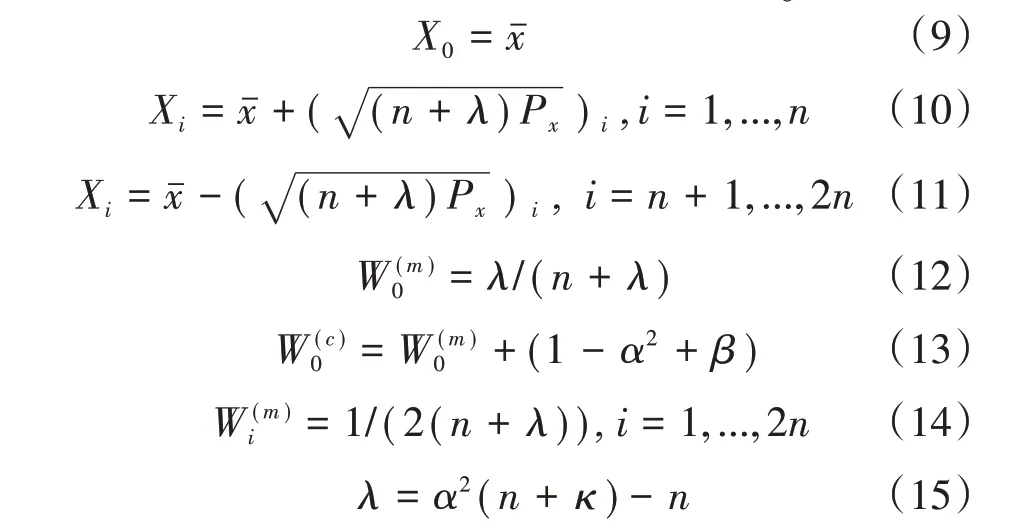
式中：κ為尺度參數，用來控制sigma 點與均值的距離；α為正的尺度參數，用以控制來自非線性函數g(x)的更高階部分的影響；β為用來控制初始的sigma點權重的參數。

縱觀現有的研究仍然存在著研究視角單一，對于組織邊界、組織域的關注較少，缺乏對于組織機制及運作邏輯的結構性分析和建構過程的討論。對于體育社會組織的制度約束、資源困境等關注過多，忽視了對于包括文化傳統、道德習俗等非正式制度對于組織運作機制的形塑過程的分析，缺乏對于中國傳統社會“合群立會”等歷史視角的社會學想象力。從研究方法上看，個案研究過多，定量研究較少，從理論的解釋力來看，理論與經驗的不匹配、理論和方法背后的邏輯推演的不清晰，引進的西方理論的適用性等問題仍存在于目前的研究當中。

對于標量情況來說，最優值為α=0,β=0,κ=2。請注意，在計算平均值和協方差時，初始的sigma點的權重是不同的。

（2）通過非線性函數傳播sigma點。

（3）計算y的均值和方差。

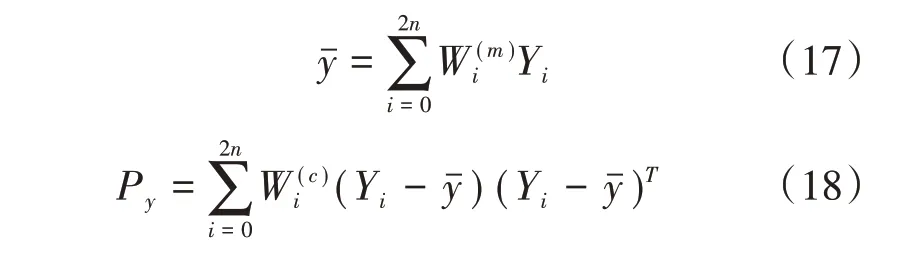
保證y的均值和協方差精確到泰勒級數2階展開。

無跡卡爾曼濾波可以通過擴展狀態空間以包含噪聲分量來實現，即。而Na=Nx+Nm+Nn則是擴展之后的狀態空間的維度，其中Nm和Nn是噪聲mt和nt的維度，Q和R則是噪聲mt和nt的協方差。整個UKF過程如下。

（1）初始化。

（2）按時間迭代。

a.用上述過程計算sigma點。

b.時間更新。

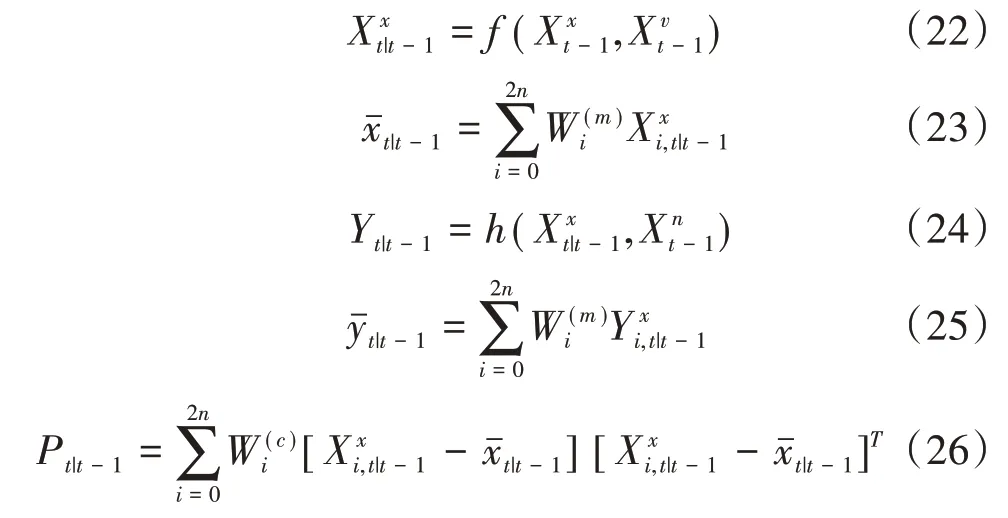
c.測量更新。

UKF 為2 階近似，所以在準確度上要勝過1 階近似的擴展卡爾曼濾波器（Extended Kalman Filter，EKF），而且在計算效率上同樣優于EKF，因為UKF不需要計算雅克比矩陣和海森矩陣。

至此已討論傳統的粒子濾波及其不足之處，隨后引入了無跡卡爾曼濾波。然而，無跡卡爾曼濾波對狀態分布做了高斯假設。另外，對于粒子濾波，可以對任意分布進行建模，但是將新的觀測加入到建議分布中并不容易。本文提出了改進辦法，在航空發動機領域，利用UKF 來為粒子濾波生成建議分布，引進最新的觀察來更新狀態估計，即為無跡粒子濾波。對于每個粒子的取值概率分布明確為

值得注意的是，即使在估計后驗分布p(xt|xt-1,y0:t)時高斯分布假設是不現實的，但對于每個粒子都有1個不同的均值和方差都不是問題。而且，使用UKF得到的均值和方差均達到2 階展開，所以系統的非線性特性得以保存。將式（32）代入到傳統粒子濾波算法中，即可得到UPF。完整的預測步驟如下。

（1）利 用式（21）～（31）的UKF 算法 來更 新,i=1,...,N，得到粒子的均值和協方差。

（3）利用式（5）計算出各粒子的權重。

（4）利用式（6）來歸一化權重。

（5）計算有效的粒子規模大小S。

（6）如果有效粒子數少于有效數閾值，則對應生成N個等權粒子。

（7）利用式（7）來計算系統狀態后驗分布的期望值。xt的條件均值可以通過xt+1=f(xt)計算得到，而xt的協方差可以通過計算得到。可以使用計算得到的條件均值和協方差來得到發動機當前時刻排氣溫度的概率密度分布[19-21]。UPF 的流程如圖1所示。

圖1 UPF的流程

2 EGTM的預測算法及實現

2.1 EGTM預測過程

系統的測量方程和狀態方程為

式中：a，b，c均為系數。

式（34）中的yt即為t時刻系統的觀測值，是航空發動機EGT 的測量值與EGT 紅線值的正差值，系統噪聲和測量噪聲均假定遵循高斯分布。根據粒子濾波方法，EGTM值估計為

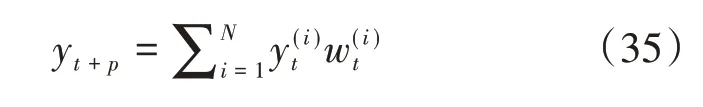
所以在t時刻的p步預測表示為

EGTM的后驗概率密度為

當設定的EGTM 閾值為Y時，達到閾值的循環為L，則

所以在t時刻預測發動機在現有EGTM 條件下得到循環閾值的概率密度分布為

2.2 仿真結果分析

在本次仿真試驗中，每次迭代中所取的粒子數均為100。采用無跡粒子濾波方法在18 和30 循環處對數據進行預測，狀態方程的參數見表1。

表1 根據歷史數據得到的狀態方程參數

35 循環處傳統粒子濾波方法的預測結果如圖2所示。

圖2 傳統粒子濾波在35循環處的預測

由于沒有考慮到最新的觀測值，采用傳統粒子濾波方法得到的數據與真實的發動機水洗循環數相差較多，預測概率密度是假定閾值為50 ℃時的數據，而當閾值為35 ℃時，預測的循環數在120 循環之后，與實際值相差較多。

在18 循環時刻的無跡粒子濾波預測結果如圖3所示。

圖3 無跡粒子濾波在18循環處的預測

前18 循環的航空發動機EGTM 實際數據將用來更新模型。從圖中可見，在達到閾值35 ℃時，預測的最終循環數為60，而實際的飛行循環數為59，預測誤差為1 循環，同時預測的EGTM 在閾值時的循環數的寬度為16。

前30 循環的發動機EGTM 實際數據將用來更新模型，如圖4 所示。在達到閾值35 ℃時，預測的最終循環數為59，而實際的飛行循環數為59，預測誤差為0 循環，同時預測的EGTM 在閾值時的循環數的寬度為7。從上述試驗結果可見，因為有更多的實際數據用以更新模型，所以模型的準確度得到了提升，模型的擬合優度統計見表2。預測的循環數的寬度收窄了，說明預測的精度更高了。

圖4 無跡粒子濾波在30循環處的預測

表2 擬合優度統計

3 結束語

隨著民航產業的飛速發展，做好航空發動機性能衰退預測，對于發動機有效及時恢復性能和節約成本具有重要意義。針對發動機領域的特點，本文所提出的無跡粒子濾波算法作為一種改進的粒子濾波方法，充分利用了最新觀測數據對系統模型進行修正，也降低了重采樣對樣本貧化的影響。因此，該方法不僅有抑制粒子退化的優點，而且在一定程度上保持了粒子的多樣性。通過對無跡粒子濾波預測結果和傳統粒子濾波計算結果的比較研究可知，無跡粒子濾波方法在預測的準確度（均值與真實值的接近程度）和預測的置信度（概率密度分布的狹窄程度）上都顯示出巨大的優勢。