一類具有飽和恢復率的隨機傳染病模型

劉 娟，陳 功

(蚌埠學院理學院，安徽蚌埠 233030)

傳染病是當今世界面臨的一個嚴重問題，傳染病的蔓延給世界各國帶來了極大的挑戰，甚至可能影響社會穩定，比如新冠病毒的傳播給現實生活造成了一定的影響，因此研究傳染病模型具有重要的實際意義。隨著傳染病動力學的深入發展，建立數學模型研究傳染病的傳播規律已成為一種趨勢。近二十年來國內外學者根據倉室模型的思想，提出了大量的傳染病模型并研究了模型的動力學性質。在已建立的傳染病模型中，以確定型模型居多[1-6]。但是在疾病蔓延的過程中，外部環境對疾病傳播有著重要的影響，這在數學上可以用隨機擾動項來表示。文獻[7]研究了下列傳染病模型：

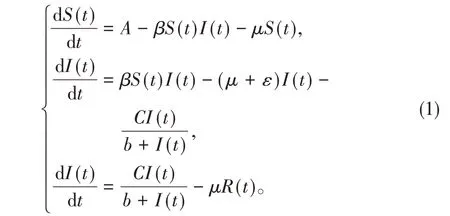
根據倉室建模的思想，(1)式中的，S(t)，I(t)和R(t)分別表示易感者、染病者、治愈者群體在時刻t的數量[8-9]。A表示易感者群體的常數輸入率，μ為，S(t)，I(t)和R(t)的自然死亡率，假設三類群體具有相同的自然死亡率。ε為染病群體的因病死亡率。為染病群體到治愈群體的恢復率函數。文獻[7]研究了模型(1)的穩定性和分支。

考慮到隨機擾動因素對疾病傳播的影響，在模型(1)中引入隨機擾動項使之變成隨機微分方程，假設外部環境主要影響參數β，用白噪聲來描述這種影響，即

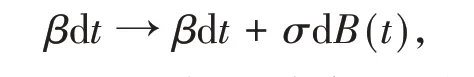
B(t)為標準布朗運動且B(0)=0，為白噪聲強度，則得到下列具有隨機擾動項的傳染病系統，

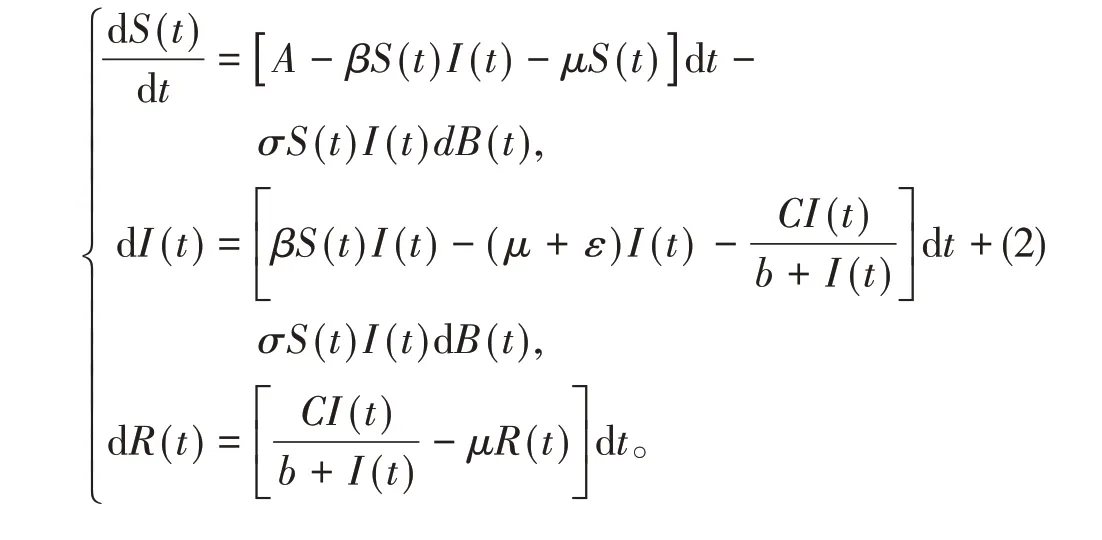
主要研究隨機傳染病的動力學性質，包括模型(2)正解的存在性I(t)及和R(t)群體的滅絕性。

1 模型(2)正解的存在唯一性

生物系統的動力學性質有多種，對于傳染病系統，是否具有全局正解是很重要的，由隨機微分方程解的存在唯一性定理知，若系統滿足局部利普希茨條件和線性增長條件，則具有唯一的正解。通過利用Lyapunov方法證明模型(2)具有唯一的全局正解。

定理 1對于任意給定的初值X(0)=(S(0),I(0),R(0))，系統（2）在t≥0 上存在唯一的解，且該解以概率1 存在于中，即系統(2)在中存在唯一的全局正解。

證明易知模型(2)滿足局部利普希茨條件，則對任意的初始條件，模型(2)存在唯一的局部解X(t)(t∈[ 0,τe])，其中τe是系統的爆破時間。證明X(t)(t∈[ 0,τe])是模型(2)的全局正解，為了證明該結論，只要證明τe∈∞a.s.即可。

設足夠大的正數k0≥1，能使X(0)都位于區間中，再k≥k0設，定義停時

規定inf ?=∞，易知τk是k的單調增函數，設，得τ∞=τe∞a.s.，若能證明τ∞=∞，則τe=∞且X(t) ∈(t＞0)。故利用反證法的思想證明τ∞=∞，若τ∞≠∞，則存在常數T＞0 及ε∈(0,1)，使得P{τ∞≤T}τ∞＞ε成立，則存在正數k1≥k0，對所有的k≥k1，有

將模型(2)相加，得

由方程初值X(0)=(S(0),I(0),R(0))，可求得

為正不變集。

定義

令T=0，則對任意，使用It?公式計算得

將(6)式代入dV的表達式得

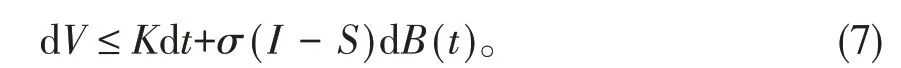
對(7)式兩邊取0到的積分，再取數學期望得

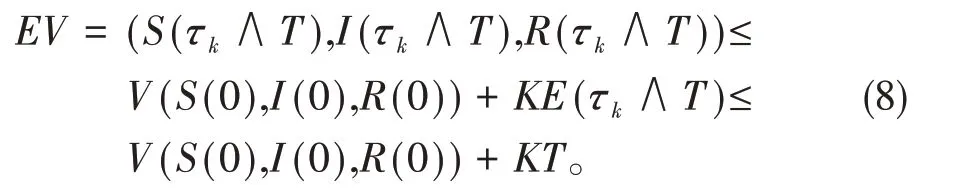
對所有的k≥k1，有P{τk≤T}＞ε。對于每一個ω∈{τk≤T}，S(τk,ω)，I(τk,ω)，R(τk,ω)中至少有一個等于k或，故有

利用(8)可得

其中Ωk={τk≤T}，1Ωk(ω)為Ωk的示性函數，令，有k→∞，

由此可知，假設不成立，故τe=∞a.s.，即模型(2)存在唯一的全局正解。

2 模型(2)疾病的滅絕性

討論在模型(2)中，染病群體及治愈者群體的滅絕條件，假設系統初始條件滿足X(0) ∈Γ?，其中Γ?為為系統(2)的正不變集。

定理2設為模型(2)的解，對于任意給定初始條件，若

證明利用It?公式，將模型(2)中含有染病群體的項改寫為

兩邊從0到t積分，并除以t，記

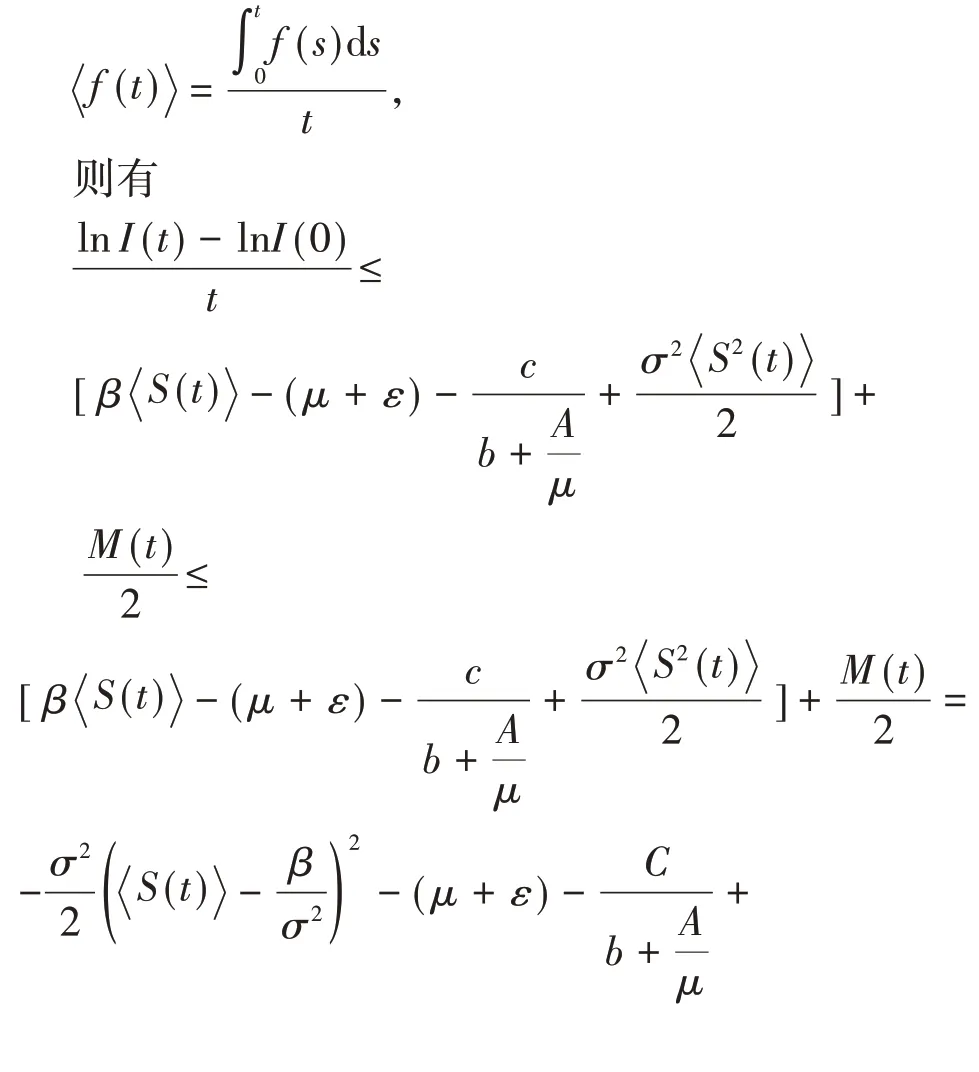
由強大數定律得

取(9)式兩邊的上極限，再將(10)式代入得

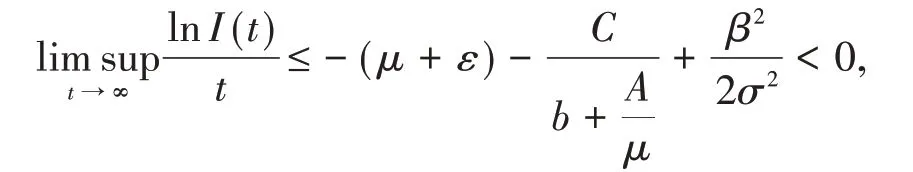
這意味著

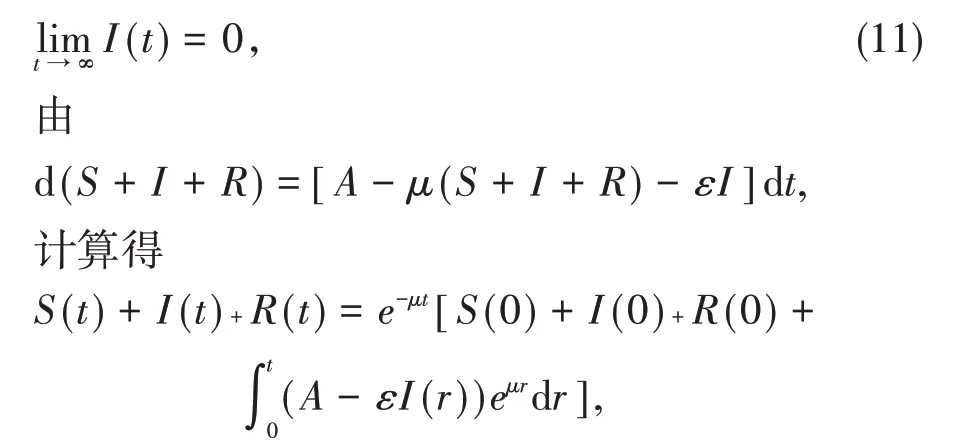
由洛必達法則及(11)式，得

系統(2)中的第三項是

由此證明了定理2。

3 結語

在文獻[7]模型的基礎上，討論了一類具有飽和恢復率的隨機傳染病模型，利用Lyapunov 泛函方法討論了模型正解的存在性及唯一性及正不變集的存在性，并使用It? 公式及強大數定律得到了染病群體及治愈者群體滅絕的充分性條件。定理2表明，如果白噪聲強度滿足一定條件，能夠保證足夠大，則I(t)、R(t)幾乎必然指數趨于0，即疾病將將消失。這說明較大的隨機擾動會對傳染病模型中的各類群體產生影響，具有重要的實際意義。