基于Morph網格變形方法的白車身模態優化

王維強，李鳳東，莊惠敏，侯 彬，吳 列Wang Weiqiang，Li Fengdong，Zhuang Huimin，Hou Bin，Wu Lie

基于Morph網格變形方法的白車身模態優化

王維強，李鳳東，莊惠敏，侯 彬，吳 列
Wang Weiqiang，Li Fengdong，Zhuang Huimin，Hou Bin，Wu Lie

（北京汽車研究總院有限公司 整車性能中心，北京 101300）

白車身模態是影響汽車振動噪聲性能優劣的重要因素，在車身CAE仿真設計階段，白車身模態頻率是最為重要的優化指標。以白車身前端橫擺模態性能優化為例，通過靈敏度分析確定關鍵結構位置，利用Morph網格變形方法將關鍵結構的截面參數化，采用序列二次規劃算法進行數值迭代優化；經過12步迭代，白車身前端橫擺模態頻率提升3.06 Hz，同時1階彎曲模態、1階扭轉模態和白車身重量3個響應得到了有效的約束控制；結果表明，該方法可以對白車身模態性能實現高效、有針對性的優化設計。

白車身模態；前端橫擺模態；Morph；靈敏度；結構優化

0 引 言

消費者對汽車舒適性的要求越來越高，振動噪聲是重要影響因素；白車身模態是控制汽車振動噪聲的重要性能指標，合理的結構設計可以獲得良好的白車身模態性能[1]。在仿真設計階段，最初的白車身模態很難滿足要求，需要通過CAE結構優化來提高其性能[2-4]。通過參數化設計變量結合SQP（Sequential Quadratic Programming，序列二次規劃）[5]、DUAL（Diffusing Update Algorithm，彌散更新算法）[6]等算法可以對性能目標函數進行快速優化。優化前通過靈敏度分析[7]篩選出對目標響應最為靈敏的關鍵結構，有效減少設計變量，提升優化效率。

設計變量的定義直接決定優化效果的好壞，其中零件厚度這一變量最為常見[8]，但改變料厚對性能提升有限，結構設計問題往往由截面、搭接位置設計不合理所致，這些因素是提升性能的根本。采用參數化建模方法，如SFE軟件（隱式參數化方法）[9]、Morph功能（網格變形方法）[10]實現梁截面、零件搭接位置等關鍵設計因素的改變。以白車身前端橫擺模態性能優化為例，提出一種通過靈敏度分析確定關鍵結構位置，進而通過Morph建模方法將關鍵結構的截面參數化，采用SQP算法對目標函數計算最優解的方法。以1階彎曲模態頻率、1階扭轉模態頻率和白車身重量3個響應作為約束條件，在滿足約束條件的前提下，得到前端橫擺模態最優的結構設計參數。此優化方法也適用于白車身其他模態的優化，具體流程如圖1所示。

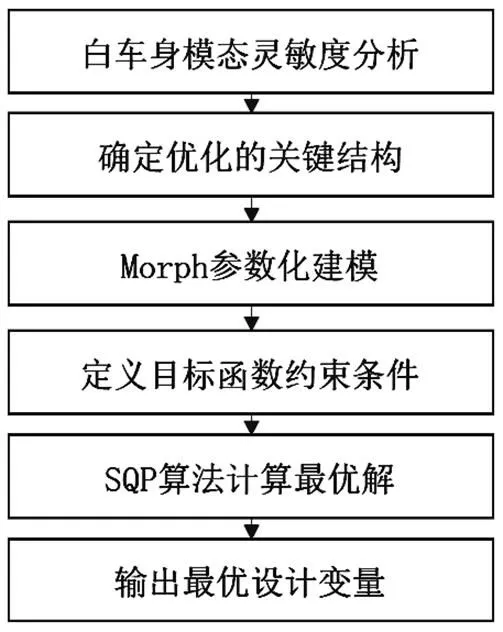
圖1 白車身模態Morph參數化優化流程

1 模態靈敏度分析

由模態分析理論可知，多自由度線性定常系統無阻尼自由振動可定義為[11]

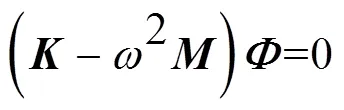
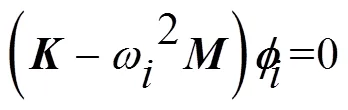
式中：為第階模態固有頻率，為第階模態振型向量。

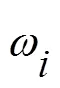
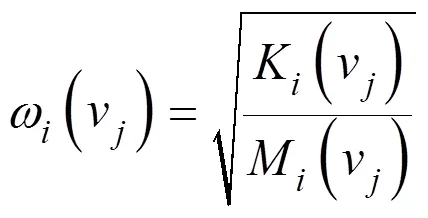
式中：K、M為通過有限元方法計算得到的第階模態剛度和模態質量，v為某個設計變量。K、M與結構形狀有關，隨v變化。

靈敏度分析是指自變量對因變量的影響程度，其數學表達為求解自變量對因變量的梯度，則各階次固有頻率的靈敏度為

通過靈敏度分析可以從復雜結構所包含的多個零件中得到對優化目標影響大的零件，從而對這些高靈敏度零件進行針對性優化，以提升目標響應優化效果，白車身模態頻率的靈敏度分析流程如圖2所示。

某車型白車身前端橫擺模態頻率的靈敏度分析結果如圖3所示，前縱梁內板對前端橫擺模態貢獻量最大，空氣室橫梁次之，此外，前縱梁外板、前圍板、前輪罩、前副車架都有較大貢獻。同理，白車身1階扭轉模態、1階彎曲模態的靈敏度分析也可以通過相同方法得到，不再贅述。

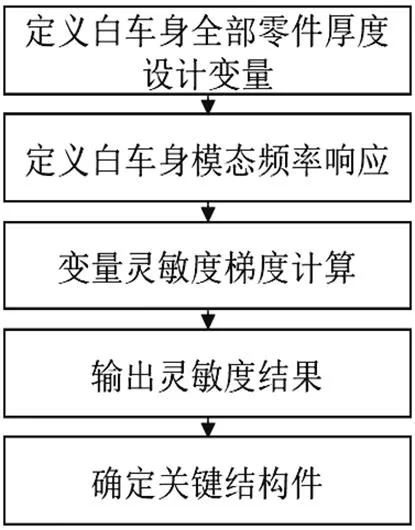
圖2 白車身模態頻率的靈敏度分析流程

圖3 前端橫擺模態靈敏度分析結果

鎖定對前端橫擺模態貢獻最大的零件是前縱梁內板后，通過增加該零件厚度可在一定程度上提升模態的固有頻率，但提升的幅度有限，尤其當與目標值差距較大時，僅改變材料厚度很難實現優化目標，同時會帶來重量和成本的大幅上升；因此，對高靈敏度零件結構的截面進行參數化優化，通常可以達到較好的優化效果。

2 Morph參數化前縱梁模型

Morph是一種針對有限元網格的參數化建模技術，通過分區控制網格節點實現有限元模型的可控結構變形[10]，可以在不嚴重犧牲網格質量的情況下快速改變結構形狀，并且可以通過定義設計變量的方式進行優化設計。針對前文白車身前端橫擺模態的優化，采用Morph參數化建模技術定義設計變量，同時定義了厚度變量。

在實際設計中，前縱梁并非嚴格的等截面梁，但其主要截面尺寸近似一致，因此前縱梁的主要截面按圖4所示來等效截面設計參數。考慮到前副車架硬點和發動機左右懸置硬點的影響，前縱梁截面高度的可變范圍很小，因此主要對截面寬度進行Morph參數化建模。

注：b為截面寬度；h為截面高度；T1為內板厚度；T2為外板厚度。

對包含前縱梁的前艙結構進行Morph參數化建模，創建網格變形區域，并對前縱梁結構設置足夠數量的控制柄實現截面形狀變形[10]，前艙結構Morph參數化模型如圖5所示。

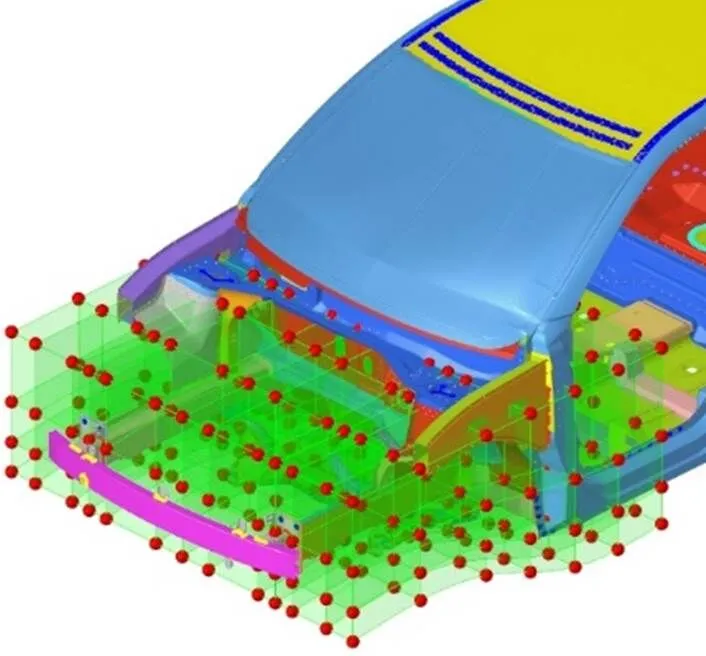
圖5 前艙縱梁Morph參數化模型

Morph參數化的前縱梁截面變形對比如圖6所示，對比前縱梁初始截面狀態和經過網格變形后的狀態，在截面尺寸變化不太大（一般低于20%）的前提下，網格變形依然滿足有限元計算的網格質量要求。

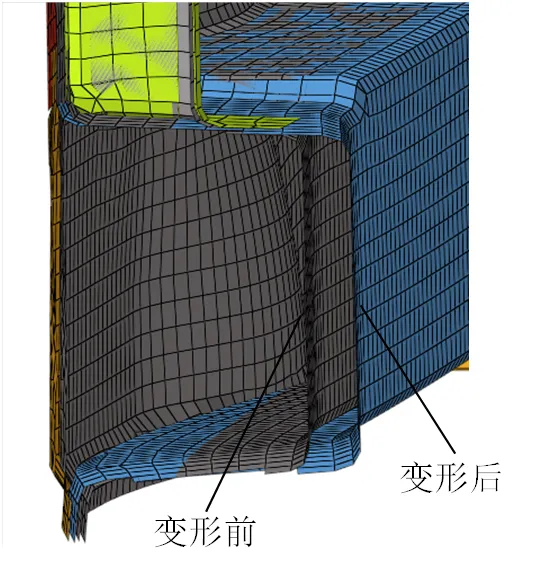
圖6 前縱梁網格Morph變形前、后對比

3 結構優化設計

3.1 優化要素

通過式（4）對優化目標計算設計變量的最優解，通常優化問題包含3個要素：設計變量、目標函數、約束條件[13]。將Morph參數化后的前縱梁橫截面寬度設置為形狀設計變量，將前縱梁內板厚度1和外板厚度2設置為厚度設計變量。根據前艙空間布置要求確定各設計變量的可變空間，見表1。

表1 設計變量空間

初始設計狀態前端橫擺模態對應的是第3階固有頻率，因此目標函數的響應為前端橫擺模態頻率3，優化目標為求解3最大值，且要求3最大值大于指標值；同時設置其他響應滿足性能指標的約束條件，包括1階扭轉模態頻率1（第1階固有頻率）、白車身1階彎曲模態頻率4（第4階固有頻率）均不能低于指標值，并且白車身重量增加量低于初始值的0.5%。由式（3）推導出前端橫擺模態頻率優化目標函數為

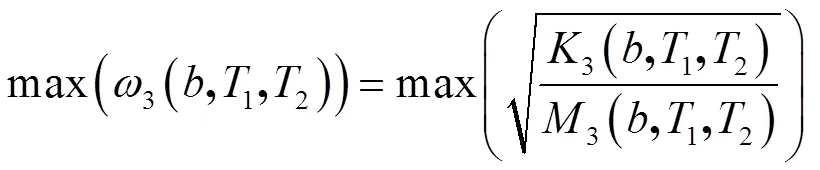
式中：3為第3階模態剛度，3為第3階模態質量。

1階彎曲模態、1階扭轉模態和白車身重量約束為

式中：0、10、20為設計變量初始值。

3.2 SQP優化流程

SQP是目前求解非線性約束優化問題最有效的方法之一，其優點是收斂性好、計算高效、邊界搜索能力強，因此受到廣泛應用。采用SQP將式（5）目標函數進行2階泰勒級數展開，將式（6）約束條件轉換為線性函數求解目標模態頻率的最優設計變量[5]，SQP優化流程如圖7所示。

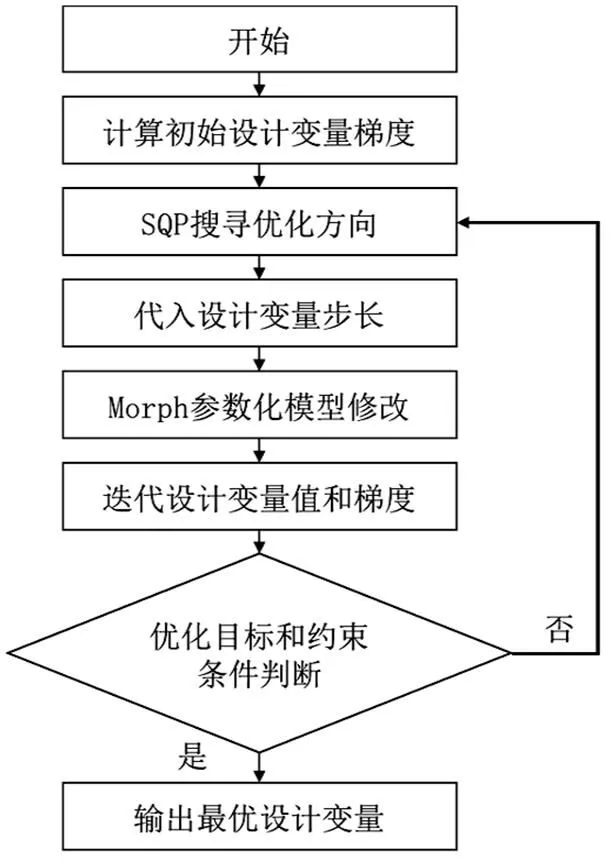
圖7 SQP優化流程

4 優化結果分析

某車型初始設計狀態的白車身模態結果見表2，1階扭轉模態頻率和1階彎曲模態頻率均滿足指標要求，但前端橫擺模態不滿足要求，需要進行優化提升。

表2 初始設計狀態的白車身模態

優化過程中白車身各階模態頻率變化情況如圖8所示。經過12次優化迭代后，目標響應3增加了3.06 Hz，增幅為8%，其在第6次迭代后達到了指標要求；在每次迭代中，約束條件的各模態頻率變化不大，且均滿足約束條件。該優化方法對目標模態頻率提升效果顯著，優化效率高。優化過程中白車身重量的變化如圖9所示，第12次迭代后重量增加1 kg，增量占初始總重量0.3%，小于0.5%，滿足約束條件要求，在性能得到顯著優化的同時白車身重量得到良好控制。

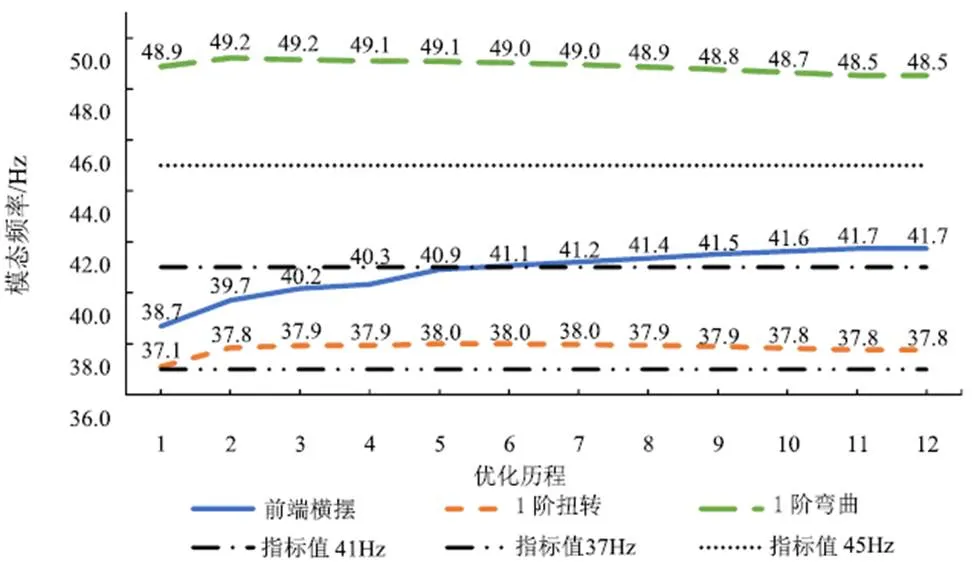
圖8 優化過程中各階模態頻率的變化

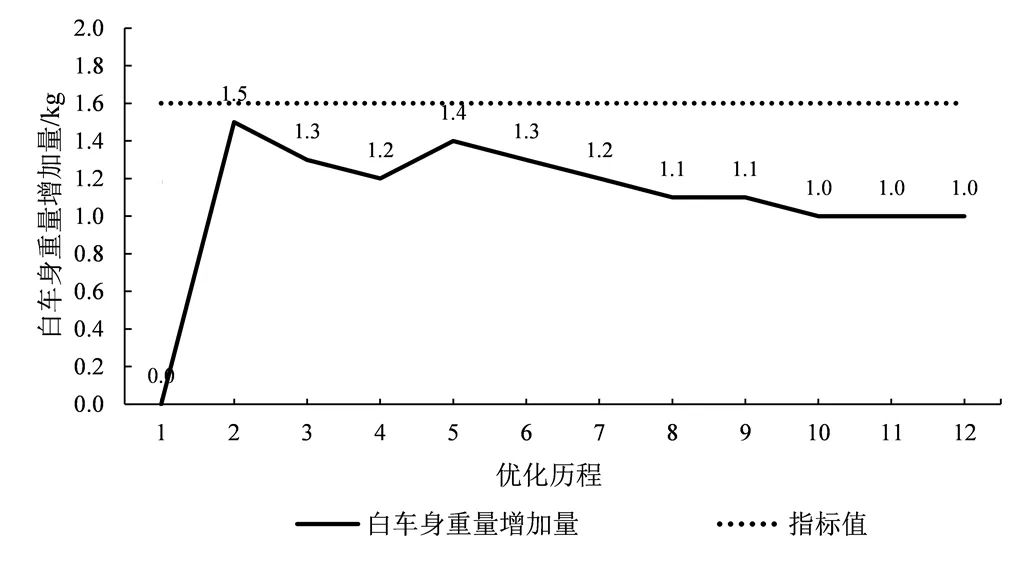
圖9 優化過程中白車身重量增加量的變化

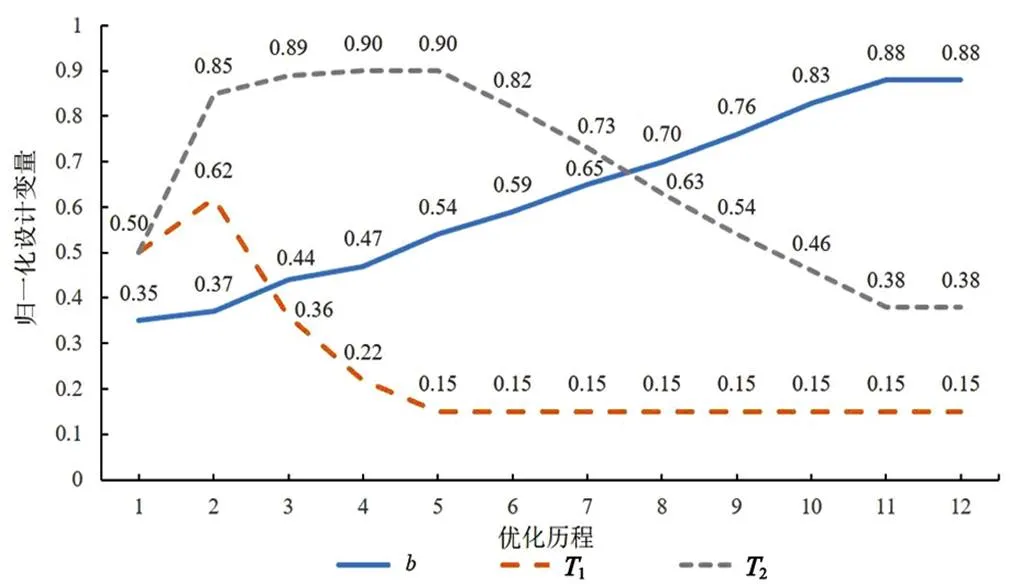
圖10 優化過程歸一化設計變量變化

優化過程中設計變量在歸一化設計空間的變化情況如圖10所示，縱坐標軸刻度值1.00、0.00分別為設計空間的上、下限。由靈敏度分析結果可知，厚度設計變量1、2與優化目標前端橫擺模態頻率成正比，即料厚增加頻率升高，料厚減薄頻率降低。而由圖8～10優化歷程中各個因素變化情況可以看出，增大截面變量在抵消料厚減薄帶來的負貢獻的同時，提升了目標模態頻率，說明截面設計變量在當前設計狀態下對于優化目標的影響最為顯著。

優化結果見表3，初始狀態前端橫擺模態和1階扭轉模態頻率間隔僅相差1.6 Hz，模態相互耦合，優化后前端橫擺模態頻率與1階扭轉模態頻率間隔提升至4 Hz，模態相互解耦，共振風險降低。

同時對比僅增加料厚的優化結果，前縱梁內、外板的料厚分別增加到設計空間允許的上限1.8、2.0 mm，與Morph優化結果的對比見表3。通過僅增加料厚方法，雖然提升了白車身的前端橫擺模態頻率，但增幅不大，僅增加了1.64 Hz，未達到指標要求；同時白車身重量增加2.6 kg，超過了Morph方法。由此可見，僅增加料厚雖然能在一定程度上提升性能，但受設計空間限制，性能提升幅度有限，難以實現針對特定性能目標的優化，同時使車身重量增加不利于輕量化。

表3 優化結果對比

5 結 論

（1）通過靈敏度分析鎖定影響性能的關鍵結構位置，進而通過Morph網格變形技術進行截面參數化優化，結合SQP算法尋找最優梯度，在設置較少設計變量的情況下，通過較少次迭代實現白車身模態頻率的優化提升。

（2）白車身的梁截面設計參數對性能的影響大于材料厚度，優化主要梁結構的截面設計參數可以獲得較為理想的優化效果。

（3）僅通過增加料厚的方式進行白車身模態性能優化的效果有限，而且使車身整體重量增加，這一方法性價比較低。

（4）截面設計變量相比料厚有更大的設計空間，可以通過優化截面參數提升性能，同時適度減薄材料厚度控制重量增加。

[1]龐劍. 汽車車身噪聲與振動控制[M]. 北京：機械工業出版社，2015.

[2]MUNDO D，HADJIT R，DONDERS S，et al. Simplified Modelling of Joints and Beam-Like Structures for BIW Optimization in a Concept Phase of the Vehicle Design Process[J]. Finite Elements in Analysis & Design，2009，45（6-7）：456-462.

[3]KIANI M，YILDIZ A R. A Comparative Study of Non-Traditional Methods for Vehicle Crashworthiness and NVH Optimization[J]. Archives of Computational Methods in Engineering，2016，23（4）：723-734.

[4]LU J，ZHAN Z，SONG H，et al. Design Optimization of Vehicle Body NVH Performance Based on Dynamic Response Analysis[J]. SAE Technical Papers，2017.

[5]GILL P E，MURRAY W，SAUNDERS M A，et al. SNOPT： An SQP Algorithm for Large-Scale Constrained Optimization[J]. SIAM Review，2001，47（1）：99-131.

[6]FLEURY C，BRAIBANT V. Structural Optimization：A New Dual Method Using Mixed Variables[J]. International Journal for Numerical Methods in Engineering，1986，23（3）：409-428.

[7]雷明準，陳劍，陳心昭，等. 靈敏度分析方法在車身輕量化中的應用[J]. 汽車工程，2009，31（7）：682-685.

[8]韓繼光，趙玉清，時玲，等. 基于模態靈敏度分析的某乘用車白車身結構優化設計[J]. 機械設計，2017，34（9）：39-42.

[9]ZIMMER H，UMLAUF U，THOMPSON J E. Use of SFE CONCEPT in Developing FEA Models Without CAD[J]. SAE Transactions, 2000, 109(6):2369-2374.

[10] Altair Engineering Inc. Altair HyperMesh User Guide[M]. 2017.

[11]傅志方，華宏星. 模態分析理論與應用[M]. 上海：上海交通大學出版社，2000.

[12]王震虎，王萬林，張松波，等. 基于車身概念模型的白車身主斷面尺寸優化[J]. 汽車工程，2018，40（8）：904-911.

[13]孫靖民，梁迎春. 機械結構優化設計[M]. 哈爾濱：哈爾濱工業大學出版社，2004.

2021-07-14

1002-4581（2021）06-0001-05

U463.82+1：TP391.9

A

10.14175/j.issn.1002-4581.2021.06.001