高壓直流附加阻尼愛克曼控制器的設計

朱顯亮，戴 濤，楊海波，徐 恩，王海浩

（國網浙江省電力有限公司舟山供電公司，浙江 舟山 316021）

0 引言

在高壓直流輸電中，如果系統只有幾個大型發電廠以及送端換流站群組成，則此系統稱之為孤島運行[1-3]。在我國西南部地區一些遠離中心城市的大型發電廠基地，電網由于運行方式的變化，孤島運行常有發生[47]。電網在孤島運行方式時，交流部分相對于直流部分的占比明顯降低，造成電力系統短路比降低。這種運行方式與非孤島運行相比，電網在受到相同擾動時系統功率更容易發生振蕩，進而引發更大的故障，造成HVDC失去穩定運行。鑒于此種情況下，研究HVDC孤島運行對于提升電力系統穩定運行具有重要意義[8]。

文獻[9-12]利用附加頻率控制法分別設計出了阻尼控制器，通過調整系統送端直流側的輸電功率，實現快速抑制系統擾動，使系統恢復正常運行，提升HVDC 在孤島運行方式下的輸電能力。文獻[9-10]利用PI控制法，通過多次改變系統比例與積分環節的參數來達到較為理想的控制效果，但PI控制法對于系統的運行方式適應性比較差，改變運行方式有可能造成PI控制器失去控制效果，對系統發生不同擾動的適應性也比較差。文獻[11-12]采用多模塊級聯的方式設計出控制器，每個模塊的控制參數需要根據一定的工程經驗來確定，對于實際工程實踐經驗要求比較高，加之設計出來的控制器參數需要反復進行調節來達到理想的效果，這就造成工作量比較大。文獻[2，13]分別采用魯棒控制與根軌跡法控制，兩者都采用單通道的控制方式，因為辨識出的傳遞函數階數比較低，這就造成設計出的控制器不能抑制系統發生的全部振蕩，對于系統發生的低頻振蕩有效果，對于系統發生的次同步振蕩效果不明顯。

鑒于以上設計控制器中存在的問題，本文提出了一種多通道帶狀態觀測器的愛克曼控制方法，對HVDC 在孤島運行方式下發生擾動時，實現對不同模態振蕩的較好控制效果。電網發生故障時，低頻振蕩與次同步振蕩往往同時發生，產生的原理又截然不同，但是通過給系統添加小的階躍擾動，卻可以辨識出不同振蕩模態下的傳遞函數，設計出各自的控制器，使電網恢復正常運行[14-16]。本文通過在多通道中添加帶通濾波器，使不同模態的信號在各自通道中定位運行。利用最小二乘旋轉不變的辨識法，對各個通道中的模態進行辨識，得到各自模態下的傳遞函數。再根據帶觀測器的愛克曼法分別設計出對應的控制器，實現同時抑制各個模態的振蕩，并設計出PI控制器與附加頻率愛克曼控制器進行對比。

1 多通道附加阻尼控制器結構

考慮到附加頻率愛克曼控制器在抑制低頻與次同步振蕩時，控制器針對不同的振蕩模態會產生正負相反的阻尼，從而使控制器失去效果。因此在每個通道中添加帶通濾波器，并根據系統存在的低頻與次同步振蕩頻率，設置好對應的濾波器頻率帶寬，使每個通道中僅有一種振蕩模態通過，減小了每個控制器之間的相互耦合影響，提升控制器之間的相互協調能力。通過調整送端功率大小，快速抑制各個模態的振蕩。使孤島運行下HVDC快速恢復穩定性。多通道HVDC 附加頻率控制器結構如圖1所示。

圖1 多通道附加頻率愛克曼控制器結構

2 附加阻尼愛克曼控制器原理

根據系統的狀態反饋方程，選取系統的控制信號，利用愛克曼控制方程求取系統的狀態反饋增益矩陣，并引入狀態觀測器，結合狀態觀測增益矩陣，最終設計出控制器。

考慮控制系統特征方程[17]為

式中:x為狀態向量；x·為狀態向 量導數；y為輸出信號；y·為輸出向量導數；u為控制信號；A為n×n維定常矩陣；B為n×1維定常矩陣；C為1×n維定常矩陣；D為常數。

選取系統控制信號為:

式中:K為狀態反饋增益矩陣。

選取適當的K值使A-BK構成一個逐漸穩定的矩陣。如果A-BK的特征值都在s的左半平面，且當t趨于無窮大時，x（t）趨于0。則其特征值為期望極點。

假設系統是狀態完全可控的，將控制信號u代入系統方程中得:

現在定義M＝A-BK

則所期望的特征方程為

式中:a i為特征多項式；μi為特征值；I為單位矩陣。

由于凱來-哈密爾頓定理闡明M應滿足其自身的特征方程，所以

利用上述方程可得確定狀態反饋的增益矩陣K的愛克曼方程

由于系統的真實狀態無法準確測量，所以引入觀測器，將觀測到的狀態再次用于反饋。這樣，在節省工作的同時，還能保證系統的可控性。從而設計出帶觀測器的愛克曼控制器[18-20]。基于愛克曼的狀態-觀測反饋控制系統如圖2所示。

圖2 基于愛克曼的觀測-狀態反饋控制系統

圖2中，x為系統真實的狀態變量，y為系統輸出值。為觀測器估計狀態變量，為觀測器輸出，K為通過最優控制優化后的狀態反饋，K e為觀測器增益矩陣。一般要選擇合適的觀測器增益值使觀測器極點比控制器極點快2～5倍。使觀測器誤差快速收斂到零。

由圖2可得觀測器狀態方程為

對式（8）取拉普拉斯變換，取觀測器初始狀態為零可得

將式（10）代入式（9）中取拉普拉斯變換得愛克曼控制器-狀態觀測器傳遞函數

3 模型搭建及參數辨識

3.1 模型搭建

對某實際HVDC電網進行建模，在電力系統仿真軟件PSCAD/EMTDC中搭建的模型如圖3所示。

圖3 孤島運行仿真模型拓撲結構

此系統中主要考慮500 k V 線路，并對220 k V輸電線路及相應的負載進行等值處理。孤島運行時系統送端容量為1 600 MW，S、M電廠各開2臺600 MW 發電機，U 電廠中只開1臺600 MW 發電機。此模型中整流側采用定電流控制，逆變側采用定熄弧控制。在孤島運行方式下，由于送端直流部分占的比重相對于交流部分比較大。因此當系統受到擾動時很容易使系統發生頻率發生振蕩，由于其短路比比較小。有可能引起系統更大的振蕩，使系統失去穩定性，給HVDC 孤島運行造成極大隱患。

3.2 傳遞函數辨識

利用TLS-ESPRIT辨識出系統孤島運行方式下的振蕩模態如表1所示。

表1 孤島運行振蕩模態辨識參數

由表1可知當系統送端功率降至25%單極運行時（送端功率為1 600 W），HVDC孤島運行模式下發生低頻與次同步振蕩。其中24.5 Hz與13.4 Hz阻尼比比較小，系統次同步振蕩比較強。0.72 Hz與0.74 Hz屬于低頻振蕩模態，其阻尼比屬于弱阻尼。

在系統處于穩定運行的狀態下，在送端整流側添加小幅階躍擾動。以直流定電流側小幅階躍為輸入，送端交流側系統頻率為輸出。首先在不添加階躍時取得數據，然后添加小幅階躍，再取數據，然后兩者差值。利用TLS-ESPRIT辨識算法，辨識出系統在不同振蕩條件下的傳遞函數。

辨識出低頻模態0.74 Hz的系統傳遞函數為

辨識出次同步振蕩模態13.4 Hz的傳遞函數為

辨識出次同步振蕩模態24.5 Hz的傳遞函數為

4 控制器參數設計

4.1 愛克曼控制器設計

在HVDC孤島運行時，以S電廠發電機送端頻率偏差為輸入，附加頻率控制信號為輸出。按照帶觀測器的愛克曼法理論設計出愛克曼控制器。通過快速調整送端直流側輸送功率，快速抑制系統頻率振蕩，使系統恢復穩定性。控制器安裝在整流側定電流處，根據不同模態的開環傳遞函數分別設計出控制器。經過平衡截斷法降階后得出低頻振蕩模態0.74 Hz的附加頻率愛克曼控制器-觀測器傳遞函數為

經過平衡截斷法降階后得出次同步振蕩模態13.4 Hz的附加頻率愛克曼控制器-觀測器傳遞函數為

經過平衡截斷法降階后得出次同步振蕩模態24.5 Hz的附加頻率愛克曼控制器-觀測器傳遞函數為

4.2 PI控制器設計

設計出附加頻率愛克曼控制器后，為比較控制器的效果，設計了PI控制器與附加頻率控制器進行對比。利用TLS-ESPRIT 辨識出包含所有模態的傳遞函數，根據[9-10]設計出PI控制器與附加頻率愛克曼控制器進行對比。比例環節參數取0.5，積分環節參數取3。其中washout為隔直環節-帶通濾波器，時間參數T＝8 s。控制器安裝在整流側直流定電流處，其結構如圖4所示。

圖4 PI控制器結構示意

5 仿真驗證

5.1 階躍擾動控制效果

設計完各個控制器以后，把上述帶觀測器的愛克曼控制器分別安裝在各自模態的通道中定位運行。PI控制器安裝在圖4所示的整流側定電流處結構中。然后通過分別添加階躍擾動以及單相接地短路擾動故障，利用搭建好的PSCAD/EMTDC模型進行仿真驗證。

1 s時在整流側直流定電流處添加0.02倍的小幅階躍擾動，使孤島運行模型的送端功率升高至1.02倍。通過PSCAD/EMTDC仿真軟件進行仿真，可得到系統低頻與次同步振蕩的仿真如圖5-7所示。

圖5 階躍擾動下送端交流側低頻振蕩模態帶觀測器愛克曼控制與無控制對比

圖6 階躍擾動下送端交流側次同步振蕩模態13.4 Hz帶觀測器愛克曼控制與無控制對比

圖7 階躍擾動下送端交流側次同步振蕩模態24.5 Hz帶觀測器愛克曼控制與無控制對比

S電廠中仿真總圖如圖8所示。

圖8 階躍擾動下送端交流側S電廠振蕩模態對比

U 電廠中仿真總圖如圖9所示。

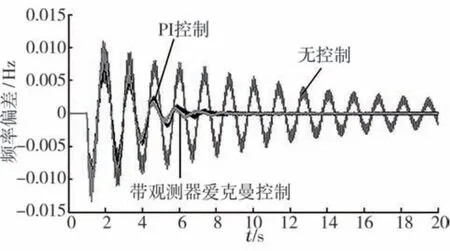
圖9 階躍擾動下送端交流側U 電廠振蕩模態對比

M 電廠中仿真總圖如圖10所示。

圖10 階躍擾動下送端交流側M 電廠振蕩模態對比

由圖5-7可知附加頻率愛克曼控制器可以較好地同時抑制低頻與次同步振蕩。由圖8-10可知，而PI控制器也有一定的效果，但其對系統各模態的抑制效果不如帶觀測器的愛克曼控制器，由此可知比例積分控制器的魯棒性能較差。

5.2 單相接地短路故障控制效果

1 s時送端交流側500 k V 母線處發生單相接地短路故障，0.2 s后故障消失，通過在PSCAD/EMTDC搭建的某實際孤島運行模型進行仿真。可得HVDC孤島運行送端交流側低頻與次同步振蕩模態的仿真圖如圖11-13所示。

圖11 單相接地故障下送端交流側低頻振蕩模態帶觀測器愛克曼控制與無控制對比

圖12 單相接地故障下送端交流側次同步振蕩模態13.4 Hz帶觀測器愛克曼控制與無控制對比

圖13 單相接地故障下送端交流側次同步振蕩模態24.5 Hz帶觀測器愛克曼控制與無控制對比

S電廠中仿真總圖如圖14-15所示。

圖14 單相接地故障下送端交流側S電廠帶觀測器愛克曼控制與PI控制振蕩模態對比

圖15 單相接地故障下送端交流側S電廠帶觀測器愛克曼控制與無控制振蕩模態對比

U 電廠中仿真總圖如圖16-17所示。

圖16 單相接地故障下送端交流側U 電廠帶觀測器愛克曼控制與PI控制振蕩模態對比

圖17 單相接地故障下送端交流側U 電廠帶觀測器愛克曼控制與無控制振蕩模態對比

M 電廠中仿真總圖如圖18-19所示。

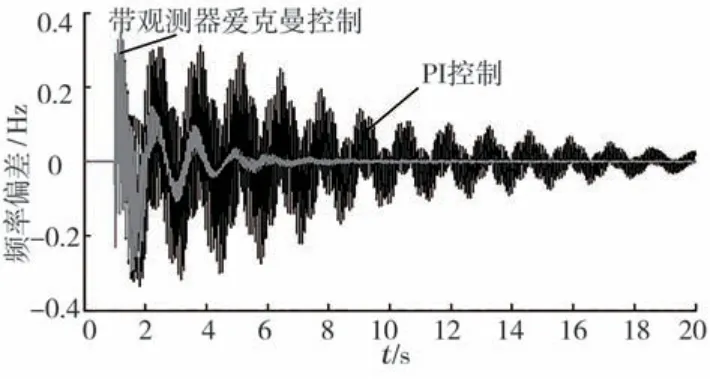
圖18 單相接地故障下送端交流側M 電廠帶觀測器愛克曼控制與PI控制振蕩模態對比

圖19 單相接地故障下送端交流側M 電廠帶觀測器愛克曼控制與無控制振蕩模態對比

通過圖11-13可知，帶觀測器的愛克曼控制器可以很好的抑制單相接地故障下，不同模態的振蕩，結合圖5-7可知對于不同的擾動，附加頻率愛克曼控制器的控制效果都比較好，有較好的魯棒性。而PI控制器的效果則不明顯。由圖8-10和圖14-19可以得出，添加不同的擾動，附加頻率愛克曼控制器的效果都較PI控制器好，PI控制器適應性比較差，可能會失去效果。

圖8 不同環境溫度下恒流充電單體電池最大電壓差

6 結論

本文利用TLS-ESPRIT 辨識算法通過給系統施加小幅階躍擾動，辨識出包含不同模態的傳遞函數。根據系統存在的低頻與次同步振蕩頻率，設置好帶通濾波器的頻率上下限參數，使不同頻率信號在各自的通道中定位運行，再次利用TLS-ESPRIT 辨識算法通過辨識得到了系統各個模態的傳遞函數。

根據系統各個模態的傳遞函數，利用本文提出的愛克曼控制原理，分別設計出不同模態對應的控制器。利用平衡降階法，兼顧控制器的魯棒性，得到階數相對較低的控制器傳遞函數。添加濾波器減小了控制器之間的相互耦合影響，提高了控制器之間的相互協調性。

為比較愛克曼控制器的優越性，設計了PI控制器與其進行對比。電力系統仿真軟件PSCAD/EMTDC仿真驗證表明，附加頻率愛克曼控制器可以較好地抑制低頻與次同步振蕩。對于不同的擾動，其效果都比較好，有較好的適應性，魯棒性比較好。而PI控制器則對于運行方式比較敏感，對于不同模態下的振蕩其效果沒有帶觀測器的愛克曼控制器好。對于添加不同的擾動，PI控制器有可能會失去效果，適應性比較差，魯棒效果不好。附加頻率愛克曼控制器采用輸出反饋，利于工程實踐。