傾轉旋翼彈性等速萬向鉸槳轂運動仿真

周 文，林 展，覃海鷹，馮萌萌

(中國直升機設計研究所，江西 景德鎮 333001)

0 引言

高速化是未來直升機發展的一個大趨勢。傾轉旋翼作為一種先進的旋翼構型，與共軸旋翼一起組成了高速直升機旋翼構型的兩大發展方向。國外，軍機方面，美國波音公司的V-22已實現批產交付，V-280已完成科研試飛；民機方面，AW609已處于取證階段，預計2022年即可交付客戶使用。國內的傾轉旋翼機的研制工作還處于起步階段。美國V-22的研制經驗表明，萬向鉸槳轂是三支臂傾轉旋翼機必不可少的關鍵部件。十字萬向鉸是機械領域最常見的一種萬向鉸構型(見圖1)。但該構型存在轉速周期波動的固有缺陷，應用于直升機時會導致全機產生較大的振動載荷，由此誘發系列的旋翼/全機動力學問題。

圖1 金屬十字萬向鉸構型

1 等速萬向鉸構型選擇

金屬十字萬向鉸構型的轉速波動關系[1]可表示為：

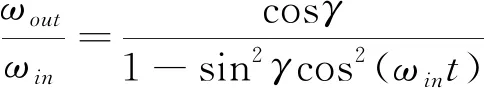
(1)

其中，ωin、ωout分別表示輸入軸、輸出軸角速度，t表示時間，γ表示傾轉角。當γ=12°時，轉速波動如圖2所示。

由圖2可知，轉速比波動幅度達2.3%。為實現等速傳動，工程上采用雙十字軸式萬向節[1]設計傳動，即兩個萬向節夾角一致，且第一個萬向節的從動叉與第二個萬向節的主動叉在同一平面。這種構型允許有較大的軸間夾角，軸承密封性好、效率高、制造工藝簡單、工作可靠，廣泛應用于越野汽車轉向裝置設計。但由于雙十字萬向節之間存在傳動軸設計，不滿足直升機槳轂尺寸緊湊的要求，該解決方案不適于傾轉旋翼機槳轂設計。

圖2 輸入軸與輸出軸成12°時的轉速波動示意

目前，國外比較成功的等速萬向鉸構型(見圖3)主要包括兩類：①基于彈性軸承的等速萬向節，例如AW609[2]、XV-15[3]、V-22[4]及 ERICA槳轂構型[5]；②基于金屬結構的等速萬向節，例如 Sikorsky研制的變直徑傾轉旋翼槳轂[6](中央使用球鉸定心，外加3個連桿傳遞扭矩)及韓國研制的無人傾轉旋翼機槳轂[7](使用球柔式等速萬向節)。

圖3 國外幾種等速萬向鉸構型示意

對比分析認為，V-22型機采用的等速萬向鉸構型(Lord公司研制)已經得到了成熟應用，很好地滿足了可靠性和維護性要求。本文僅針對彈性等速萬向鉸開展設計及驗證工作。

2 彈性等速萬向鉸構型分析

彈性等速萬向鉸主要結構如圖4所示。萬向鉸功能結構件主要由彈性萬向鉸軸承、中心件、連接件和三組彈性連桿構成。其中，中心件與旋翼主軸相連，負責主軸扭矩的傳遞；萬向鉸軸承實現揮舞運動及揮舞切力的傳遞；三組彈性連桿的兩個端頭均為彈性關節軸承，與中心件連接，以此來實現主軸扭矩的傳遞和運動協調。此外，這種構型設計使得旋翼旋轉時，交變扭矩在槳轂處自平衡(如圖5所示)，即沒有交變扭矩傳遞到旋翼軸上，不會引起不利振動。

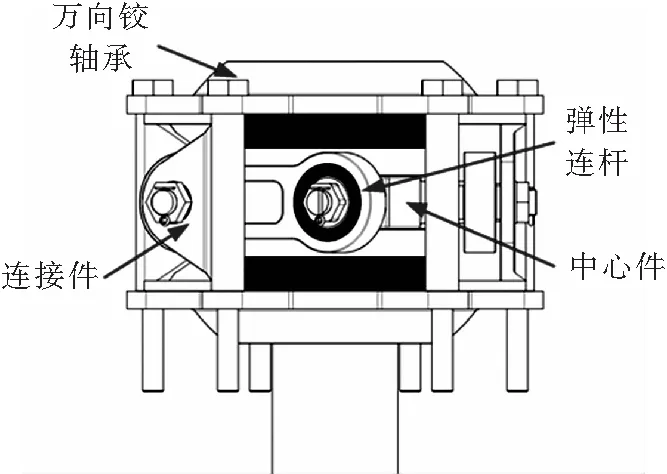
圖4 彈性萬向鉸構型

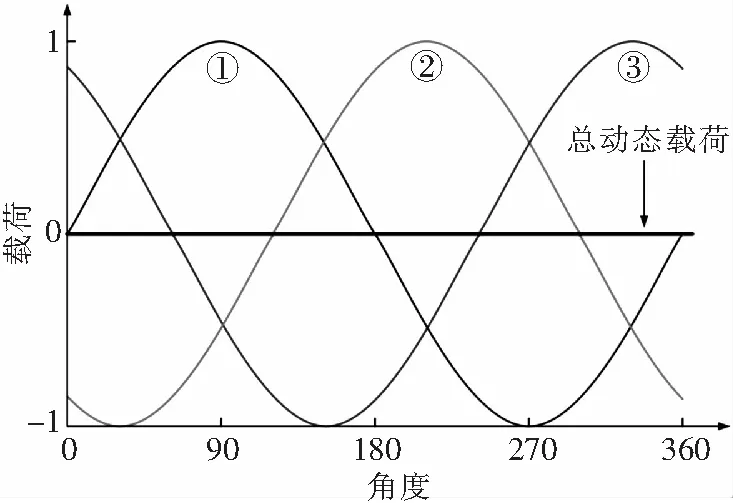
圖5 彈性萬向鉸交變力矩

3 彈性等速萬向鉸等速原理

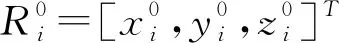
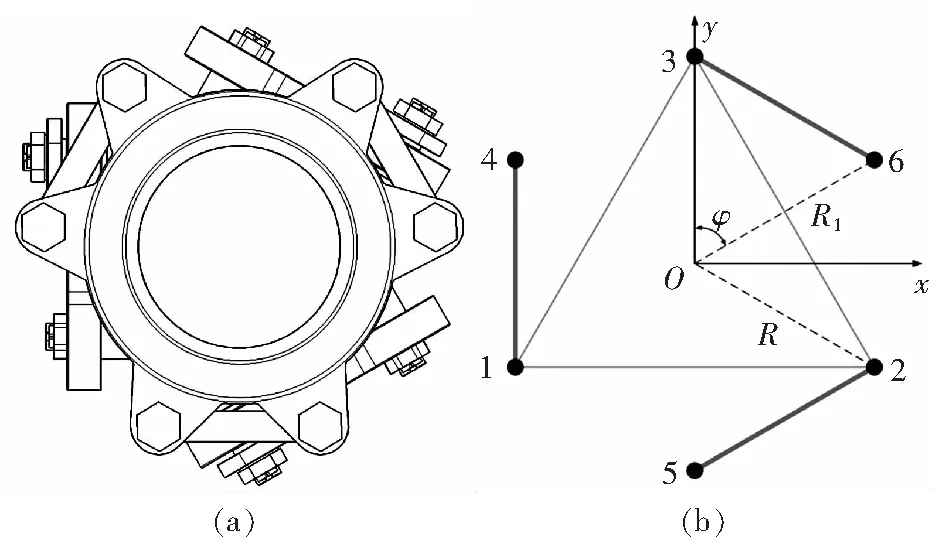
圖6 彈性萬向鉸實物模型(a)及簡化示意(b)

這里，上標“0”表示初始時刻，上標“T”表示轉置。

將槳轂盤面傾轉γ角度(簡單起見，繞y軸旋轉)，在三組彈性連桿的作用下，標號4，5，6三個點構成的平面(記為∑2)仍然過坐標原點O。建立如圖7所示的坐標系O-x′y′z′。

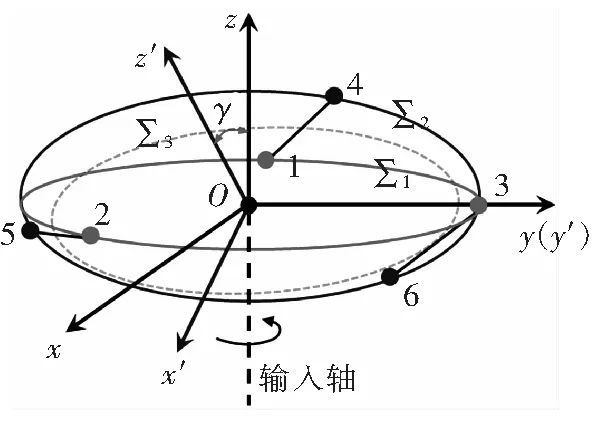
圖7 槳轂盤面傾轉角度后的坐標系示意

其中，z′軸垂直于∑2。與中心件固連的軸承中心(標號1, 2, 3)構成的平面記為∑1。坐標系O-xyz與O-x′y′z′之間的對應關系為：

(2)

設t時刻，旋翼主軸、槳轂盤面分別旋轉θ1(t)、θ2(t)角度。此時，與中心件固連的三個軸承中心(標號i=1, 2, 3)在O-xyz坐標系下的坐標為：

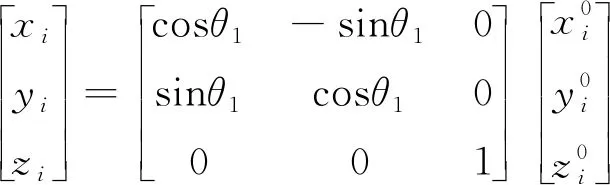
(3)

相應地，與中央件固連的三個軸承中心(標號i=4, 5, 6)在O-x′y′z′坐標系下的坐標為：

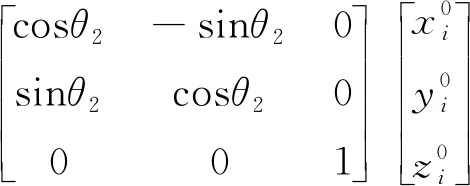
(4)

這里，上標“0”代表初始時刻。

根據O-xyz與O-x′y′z′之間的對應關系可知，與中央件固連的三個軸承中心(標號i=4, 5, 6)在O-xyz坐標系下的坐標為：

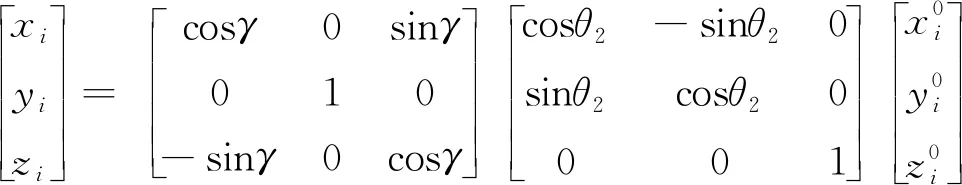
(5)

顯然，在旋轉過程中，三組彈性連桿的中心的運動軌跡相同，且構成的旋轉面(記為∑3，如圖7綠色虛線所示)始終過原點O。在O-xyz坐標系下，設∑3的平面方程為：

Ax+By+Cz=0

(6)

事實上，在槳轂盤面傾轉的瞬間，軸承組3-6及2-5的中心均在平面∑3上，即有：

令R1=βR，化簡式(7a)、式(7b)，得：

Aβsinφcosγ+B(1+cosφ)-Cβsinφsinγ=0

(8a)

根據上述兩式，解得：

A=β(β+cosφ)sinγ

(9a)

B=βsinφsinγ

(9b)

C=β2cosγ+βcosφ(1+cosγ)+1

(9c)

由于旋轉過程中，軸承組3-6的中心始終位于平面∑3上，故有：

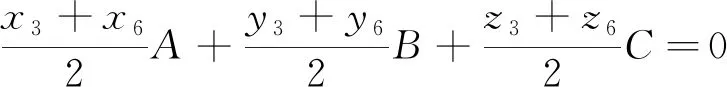
(10)

其中，

化簡式(10)，得：

sin(φ-θ1)-sin(φ-θ2)(1+βcosφ)-

βsinθ1+βsinφcos(φ-θ2)=0

(12)

進一步整理，得：

β(sinθ2-sinθ1)+sin(φ-θ1)-sin(φ-θ2)=0

(13)

根據三角函數和差化積公式，式(13)可化為：

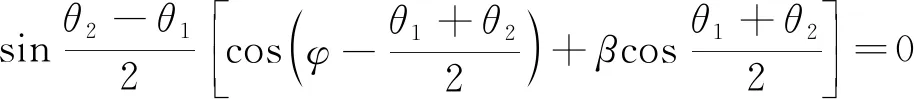
(14)

顯然，當t連續變化時，要使式(14)恒成立，只有

θ2(t)-θ1(t)=2kπ,k∈Z

(15)

結合初值條件θ2(0)-θ1(0)=0，知式(15)中k=0，即：

θ1(t)=θ2(t)

(16)

因此，旋翼主軸與槳轂盤面轉速相等，證實該彈性萬向鉸構型滿足等速設計預期。

4 彈性等速萬向鉸運動仿真

首先，進行彈性連桿兩端關節軸承的徑向長度計算。

不失一般性，以軸承組3-6的徑向長度計算為例。根據式(11)，易得：

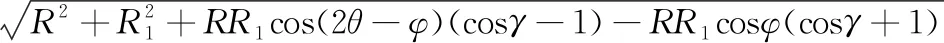
(17)

其中，θ表示任意時刻的旋轉角度(根據等速原理，知θ1=θ2=θ)。其它兩組彈性連桿的長度可類似得到，這里不再贅述。

圖8給出了R=200 mm，γ=10°時，三組彈性連桿的徑向長度隨時間的演化曲線。由圖可以看出，d3,6和d2,5的初始值均為200 mm，而d1,4的初始值卻大于200 mm；三組彈性連桿的徑向長度均呈周期變化，且單個彈性連桿的實際伸縮位移幅值約為3 mm。這是三支臂傾轉旋翼彈性萬向鉸槳轂的連桿只能選用彈性連桿(而非金屬連桿)的一個最直接的原因：在旋轉過程中，連桿組件需要彈性軸承實時補償位移。

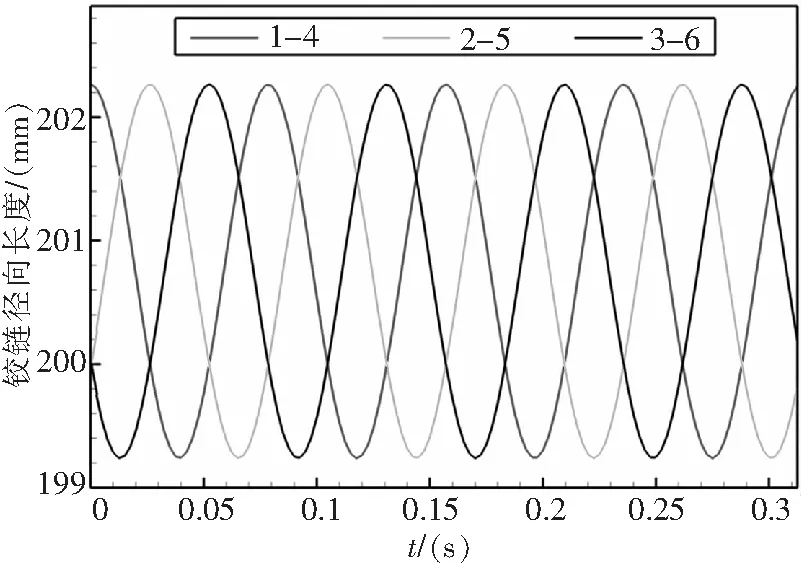
圖8 三組彈性連桿的徑向長度隨時間的演化

其次，驗證旋轉主軸與槳轂盤面的轉速波動為零。具體方法為：

1)根據經驗估計出彈性連桿所需的徑向剛度Kr，這里取Kr=40 kN/mm；

2)根據式(20)，計算彈性連桿的實際伸縮位移Δdi,i+3，進而得出彈性連桿徑向載荷Fi,i+3(Kr,Δdi,i+3)；

3)計算輸入、輸出軸的合力矩∑Min、∑Mout，驗證二者是否為零。

簡單起見，這里暫不考慮彈性連桿扭轉、彎曲及任何氣動外力的影響，傾轉角γ=10°。圖9給出了輸入、輸出軸總力矩的模隨時間的變化過程，可以發現輸入、輸出軸的總力矩為零，從而驗證了輸入、輸出軸轉速相等。圖10給出了三組彈性連桿固支端、活動端及中心點的運動軌跡。從圖10可以看出，三個點的旋轉軌跡共圓心。圖11給出了不同傾轉角度下，彈性連桿3-6的相對徑向位移隨時間的演化。圖11顯示：彈性連桿的實際伸縮位移幅值隨著傾轉角的增大而增大，且增長趨勢呈非線性變化。

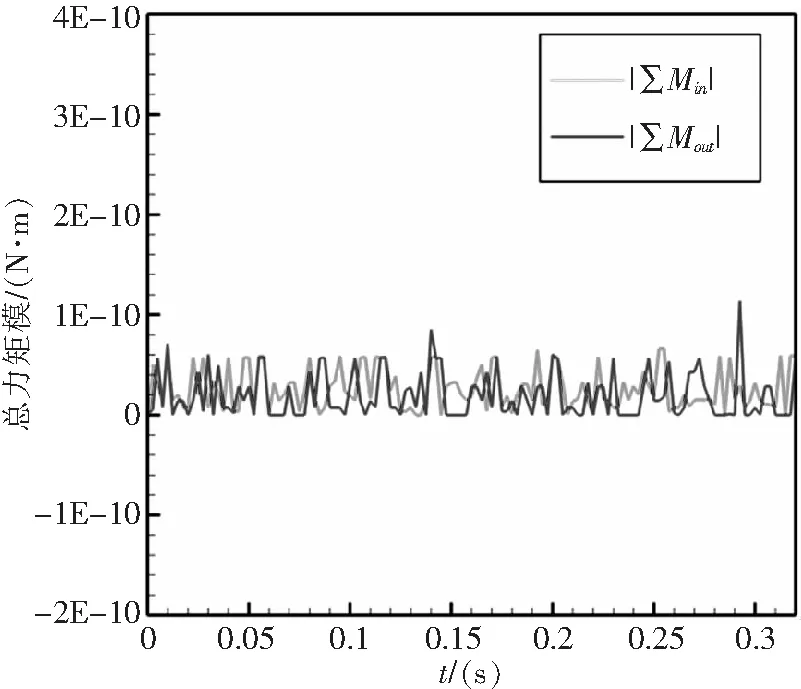
圖9 輸入、輸出軸總力矩的模隨時間的演化

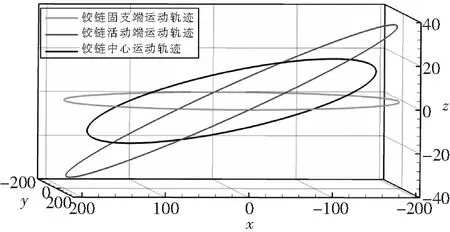
圖10 彈性連桿固支端、活動端及中點的運動軌跡(單位: mm)

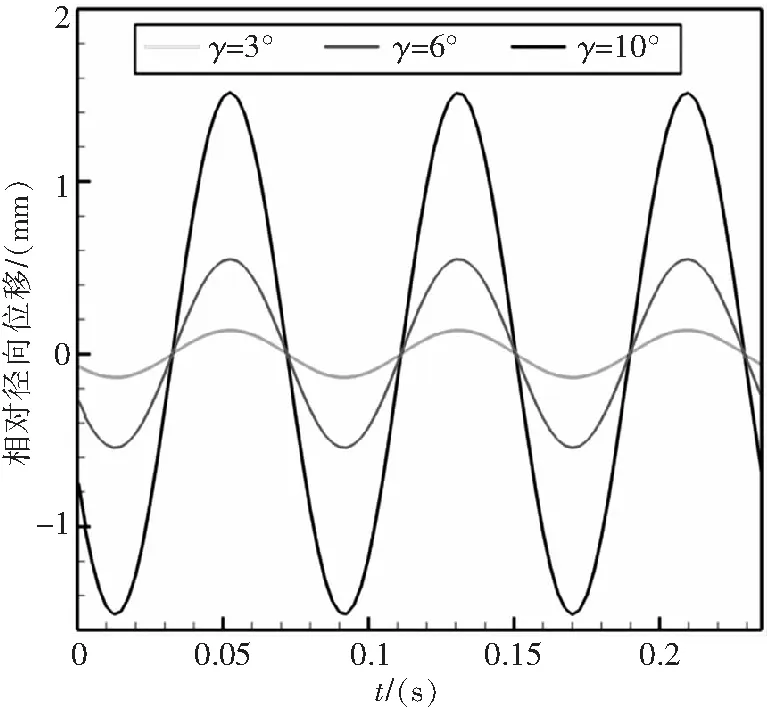
圖11 γ不同時，彈性連桿3-6的伸縮位移隨時間的演化

最后，考慮空氣阻力對彈性連桿伸縮位移的影響。這里忽略彈性連桿的彎曲，傾轉角γ=10°，Kr=40 kN/mm，空氣阻力方向與槳轂盤面旋轉速度方向相反，大小設為1000 N。圖12給出了空氣阻力對彈性連桿3-6的徑向長度的影響。從圖12可以看出，考慮空氣阻力后，彈性連桿的徑向長度整體變大，但各時刻的增加量并不相同。這是因為彈性連桿在克服空氣阻力時，徑向載荷增大，從而徑向長度變大。另一方面，在旋轉過程中，彈性連桿方位角不斷變化，空氣阻力在徑向的分量也隨之發生變化，因此彈性連桿徑向長度在各時刻的增加量并不相同。

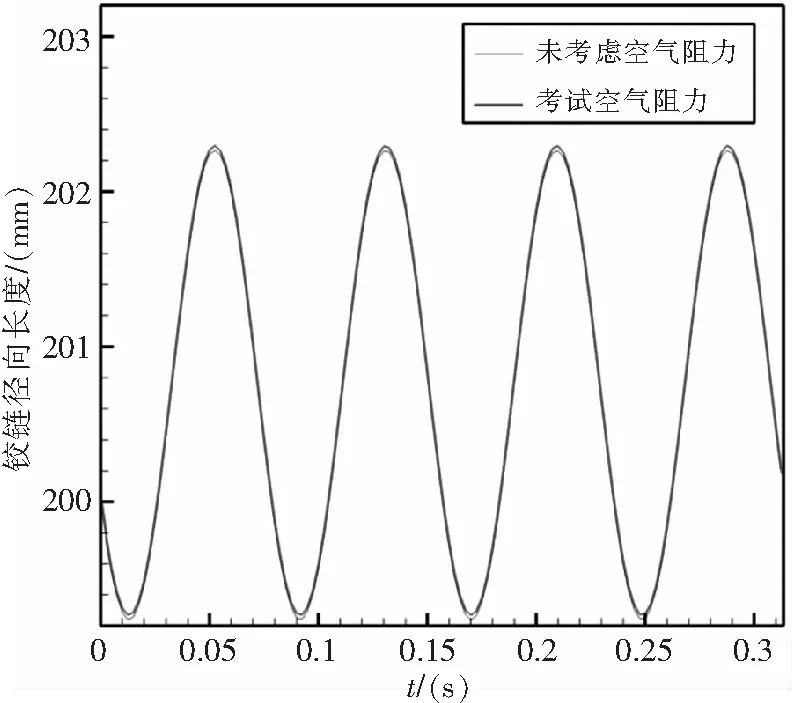
圖12 彈性連桿3-6的徑向長度隨時間的演化

5 結論

本文首先給出了一種彈性等速萬向鉸構型，然后詳細證明了其等速原理，最后基于等速原理建立運動仿真模型，進行了運動仿真分析。得到了彈性連桿徑向長度和輸入、輸出軸總力矩模在旋轉過程中隨時間的演化規律，以及槳轂盤面傾轉角度、空氣阻力對彈性連桿徑向位移幅值的影響情況。仿真結果一方面從理論上驗證了彈性萬向鉸的轉速波動為零，另一方面可結合外部載荷輸入，為彈性連桿的徑向剛度指標設計提供理論依據。此外，本文為復雜氣動載荷狀態下彈性等速萬向鉸的運動仿真、零部件之間的運動干涉檢驗以及相關指標設計的進一步優化奠定了基礎。