串列雙圓柱繞流噪聲計算方法對比研究

瞿 堯 劉滟鈺 王 寧 柴應彬 楊 平 張詠鷗*

(武漢理工大學船海與能源動力工程學院1) 武漢 430061) (星云智熵科技有限公司2) 北京 100020)

0 引 言

在流體力學和流體聲學的研究過程中，鈍體繞流問題一直是重要的研究課題之一.隨著大型客機的迅速發展，越來越多學者對飛機噪聲進行了研究.Chow等[1]對大型客機A340進行了實驗研究.實驗結果表明:起落架的噪聲比襟翼噪聲要高6 dB，圓柱繞流噪聲對飛機具有很大的影響.相比于單圓柱繞流，雙圓柱繞流更符合實際情況，現實中更多的是流體在多個物體之間的相互作用下流動.研究雙圓柱繞流產生的噪聲中，上游產生的渦會作用在下游圓柱面上產生更小的渦，下游產生的渦脫落具有更為復雜的流動特性，這對復雜的氣動噪聲研究具有重要價值.

美國航天局(NASA)研究中心[2]在空氣動力學基礎研究風洞(BART)和靜流設備(QFF)風洞中進行了大量的空氣動力學和氣動噪聲試驗.國內外學者參照這些試驗的模型做了很多研究，Lockard等[3]利用三維求解器 CFL3D模擬計算了串列雙圓柱繞流，利用 FW-H 方程計算得到遠場噪聲，得到了與試驗結果吻合的計算結果.Papaioannou等[4]比較了雙圓柱的三維模擬同二維模擬的區別，結果表明，三維模擬能更好地模擬尾跡的渦量場、圓柱表面受力及渦脫落頻率，得到了與實驗更接近的臨界間距比.趙超等[5]基于不同RANS模型的DES方法研究了雙圓柱繞流表面壓力系數均方根值的對比，得出SST-Kω模型對比試驗有較好的吻合.馬瑞軒等[6]基于SST-SAS自適應尺度模擬結合FW-H方法計算了雙圓柱繞流流動特性和聲場特性.趙威等[7]建立與試驗模型相當的展長并利用Lighthill聲類比方法求出遠場聲壓.劉國慶[8]通過Lighthill聲類比方法得到很好的仿真結果，并對圓柱的間距、排列雷諾數對噪聲的影響作了分析.

基于此，文中通過LES方法計算標準雙圓柱繞流模型，利用基于有限元求解變分形式的聲類比方程和基于面積分求解聲類比方程計算遠場噪聲，分別采用聲學計算軟件ACTRAN和流場計算軟件Fluent中的聲學模塊計算，并分析兩種方法存在的差異性.

1 數值求解理論

1.1 大渦模擬

大渦模擬(large eddy simulation，LES)是最近幾十年來興起的重要數值模擬方法，它主要通過濾波函數處理Navier-Stokes(N-S)方程，過濾掉較小尺度的渦，然后精準計算該尺度以上所有湍流的運動.

濾波器公式定義為

(1)

式中：D為流體域；G為決定大渦尺度的濾波函數.

將空間區域離散后得到有限控制體積.

(2)

式中：V為控制體積

濾波器函數G(x,x′)取為

(3)

將N-S方程經過濾波函數過濾過后，得到如下方程.

(4)

式中：τij為亞格子應力張量，定義如下.

(5)

亞格子應力張量τij的計算需要建立亞格子應力模型計算，基于Boussinesq假定，引入了大尺度應變率張量Sij和亞格子黏性系數υsgs，計算公式為

(6)

式中：υsgs為小渦的黏性系數，而大尺度應變張量Sij的計算公式為

(7)

目前常用的亞格子應力模型有Smagorinsky模型、WALE模型、動態Smagorinsky模型.本文使用更容易收斂的Smagorinsky亞格子應力模型.

1.2 聲類比方程

面積分聲類比方程是通過引入廣義函數，通過N-S方程整理得到的，也是聲比擬方程中最常用的形式，具體形式為

(8)

式中：

ρ0為遠場流體密度；p′為遠場聲壓；c0為遠場聲速；f為積分表面；ui為xi方向上的速度分量；un為f=0面上的法向速度；vn是物面速度的法向分量；δ(f)為狄拉克函數；H(f)為赫維賽德階躍函數；Tij為Lighthill聲類比應力張量；pij為表面載荷.式(8)右邊第一項為單極子聲源，第二項為偶極子聲源，第三項為四極子聲源.

2 計算模型介紹

2.1 流場計算模型

采用NASA在消聲室做的QFF模型試驗，該試驗下風速Uo=43.4 m/s.試驗中，兩個相同直徑的圓柱沿著風口依次串聯排列，其中圓柱直徑D=0.057 15 m，雷諾數計算為Re=1.66×105，兩個圓柱之間的中心距離為Lz=16D.選取3D作為模型展長,然后利用文獻[8]的修正方案修正結果.為了充分捕捉繞流過后的聲源，使結果更加的準確.取上游段長度為L1=5D，下游段長度L2=16.3D，整個外流域尺寸24D×11D×3D，建模時圓心取在上游圓柱底部圓心處.

由于計算的模型為高雷諾數下圓柱繞流，圓柱尾部會產生大量不同尺度的渦，為了充分捕捉不同尺度的渦來提高計算精度，對圓柱周圍及圓柱尾流部分進行加密處理.采取結構化網格劃分，網格總數為350萬，圖1為俯視平面的網格圖.

圖1 網格示意圖

流場入口邊界條件為速度入口，出口邊界條件為壓力出口，上下壁面為周期性邊界，圓柱壁面為無滑移壁面.流場先進行定常計算，采用的是標準k-ε模型，然后取時間步長Δt=0.001 s，計算一定步數后，待模型收斂效果很好時，進行LES模型計算，Δt=2×10-5s.待LES模型計算收斂時，提取非定常流場計算結果，時間步數設為25 000步，計算時間即0.5 s，每隔25步保存A個結果，得到1 000個采樣數據.

2.2 模型介紹

基于變分形式聲類比方程的ACTRAN聲學模型中，整個計算網格域分為聲源域、傳播域、無限域三個部分，見圖2.

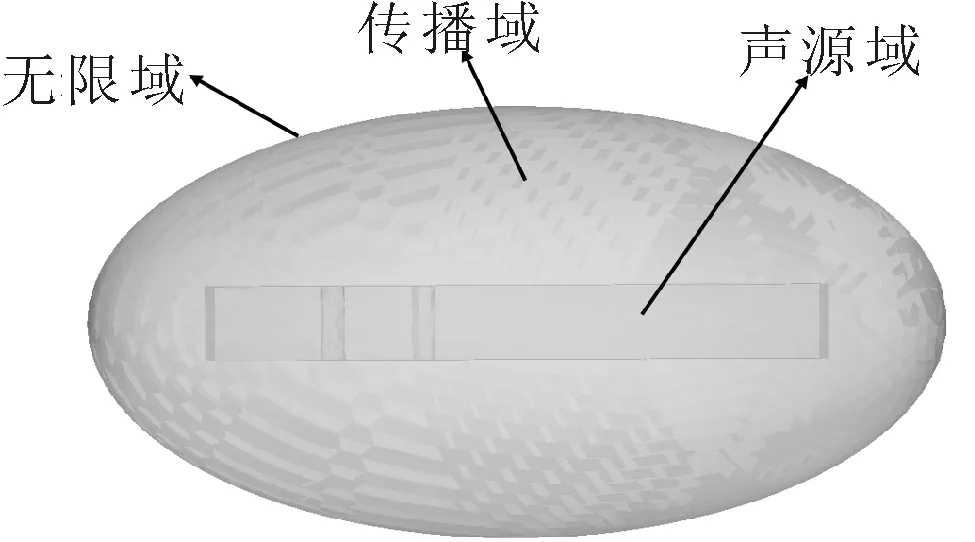
圖2 雙圓柱繞流聲學計算模型

ACTRAN聲學軟件當中，為了更直觀的觀察聲學信號，通過傅里葉變換將時域下的瞬態流場信息轉化為頻域下的流場信息.其中，轉化后的分辨率Δf=1/(N·Δt)，聲學計算得最高頻率fmax=1/(2n·Δt).所以，計算所得的聲學信號分辨率為2 Hz，最高聲學頻率為1 000 Hz.

而基于面積分聲類比方程直接計算寬頻帶噪聲，由于計算的低馬赫數下圓柱繞流問題，忽略四極子聲源，只考慮壁面上的偶極子聲源.因此在聲學模塊中選擇圓柱壁面為噪聲源，數據保存和ACTRAN一致.

為了驗證流場計算結果的準確性，見圖3.

圖3 壓力系數測點位置示意圖

取圓柱中間截面，以圓柱中心為坐標原點，圓柱駐點為起始點，順時針方向每隔10°取一個監測點.計算上、下游圓柱表面的壓力系數和壓力均方根系數，與試驗結果進行對比.其中壓力系數計算公式為

(9)

式中:p0為參考聲壓；ρ0為流體密度；u0為流速.

三維建模原點位置在上游圓柱底部中心處，遠場噪聲監測點以(9.11D，-2.4D，1.5D)為圓心，布置A(-8.33D，27.715D，1.5D)、B(9.11D，32.49D，1.5D)、C(26.55D，27.815D，1.5D)三個監測點，將仿真模擬計算得到的聲學結果與試驗比較.

3 流場結果分析

3.1 壓力系數

圖4為上、下游圓柱表面各測點的壓力系數.整體具有很好的對稱性，壓力系數從駐點角度開始向兩邊先下降到最低點，然后上升到流動分離點時壓力系數趨于平緩，平緩的這一部分圓柱表面的剪切力趨于零.

圖4 上、下游圓柱表面各點壓力系數

表1為分離點角度對比表，由表1可知，上、下游的壓力系數與試驗值吻合的很好，渦脫落分離點都與試驗接近，最大分離點誤差為3.7%.說明了流場計算結果可靠，可以作為后續計算聲場的流場結果.

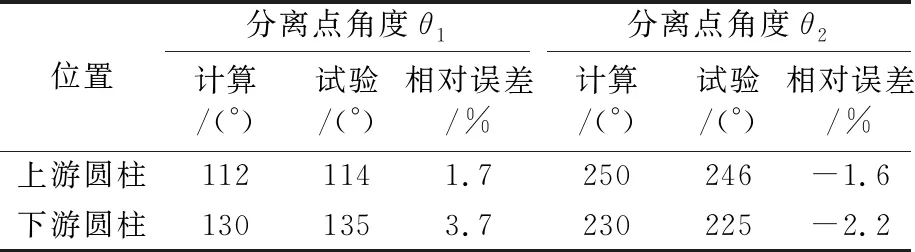
表1 分離點角度對比表

3.2 流場特性分析

渦脫落是圓柱繞流的重要特征之一，而雙圓柱繞流的渦脫落比單圓柱繞流的渦脫落要復雜的多，圖5為雙圓柱繞流X-Y截面和X-Z截面速度云圖.

圖5 截面云圖

由圖5可知，兩個圓柱下游部分存在著不同尺度的渦，由渦聲理論可知，漩渦的產生、拉伸、變形、和破碎都會產生噪聲，這也是繞流的主要噪聲來源，結合漩渦結構能夠很好的知道圓柱繞流的發聲機理.為了更加形象的看出繞流產生的脫落渦，圖6為雙圓柱繞流的速度渦量云圖.

圖6 速度渦量云圖

由圖6可知，上游圓柱存在著周期性脫落的漩渦，上游脫落渦抨擊下游圓柱表面產生了大量的破碎渦，同時自身也產生不同尺度的脫落渦，這部分是整個流場發聲的主要部分.

4 聲場結果分析

由于本文計算的展長為3D，而試驗計算的展長為16D，所以需要引入一個修正系數來減小由于展長差異造成的影響.采用文獻[8]的修正方法，具體形式為

當LC≤LS

SPL=SPLS+10 lg(L/LS)

(10)

當LC≤LS≤L

SPL=SPLS+20 lg(LC/LS)+10lg(L/LC)

(11)

當L≤LC

SPL=SPLS+20lg (L/LS)

(12)

式中：SPLS為數值計算得到的聲壓級；L為實驗的展向長度；LS為數值計算得展向長度；LC為展向相關尺度.

修正中所用到的展向相關尺寸是不同頻率和不同位置的函數，因此不同頻率下的修正值都應該是不相同的.鑒于目前展向修正方法并不太完善，文中采用相同的相關尺度進行修正，認為所有頻率下LC=4D，則計算得結果修正值為9.77 dB，得到的聲壓級頻譜圖見圖7.

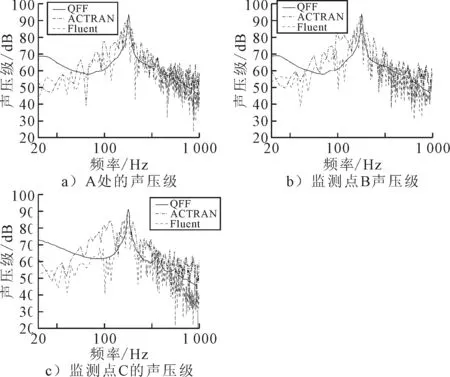
圖7 三個監測點頻域聲壓級

由圖7可知，在100～500 Hz以內結果與試驗結果吻合度比較好，500 Hz以上和100 Hz以下的差異是由于試驗風洞上下是由兩塊平板固定圓柱，能量會被剛性平板反射出去，而流場計算時上下壁面采用的是周期性邊界.

表2～3為三個監測點仿真的峰值頻率和峰值聲壓級，與實驗結果進行了比較.

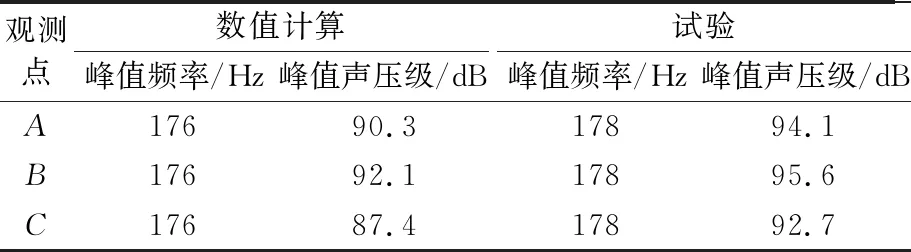
表2 ACTRAN計算的峰值聲壓對比結果

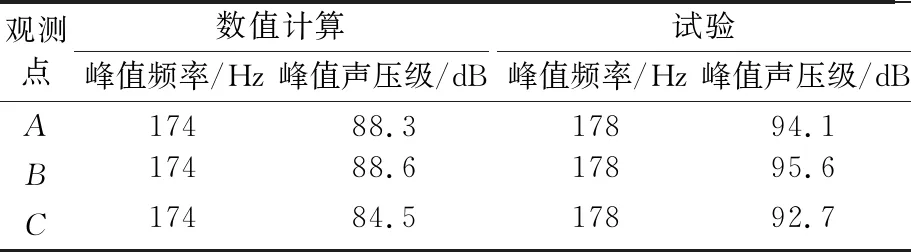
表3 Fluent聲學模塊計算的峰值聲壓對比結果

由表2～3可知，峰值聲壓級和頻率與試驗量級相差很小，二者之間峰值頻率的差異主要是由于數值模擬中無法模擬實驗中轉捩帶讓渦脫落提前這一現象造成的.

5 結 束 語

文中分別采用聲學軟件ACTRAN和計算流體動力學軟件Fluent中的聲學模塊，即采用基于有限元求解變分形式聲類比方程和基于面積分求解聲類比方程兩種計算方法，計算了雙圓柱繞流的流動特征和聲場特征，并且和NASA的QFF試驗進行了比較.對于峰值頻率和聲壓級，經過修正的ACTRAN計算更接近于實驗值，峰值聲壓級誤差為1.1%，峰值頻率誤差為4.5%.而Fluent聲學模塊計算的聲壓級誤差為2.2%，峰值頻率誤差為7.4%.兩種計算方法采用了相同的流場結果，只是噪聲計算方法不同，但都能比較好的與試驗結果進行吻合，這表明了計算方法的合理性.對軍事領域最大聲壓級要求精度較高的可以采用ACTRAN軟件，而對于工況眾多的工程問題，可以采用更為方便的Fluent聲學模塊.