含初始變形的薄板十字形焊接接頭疲勞強度評估

韓鑫宇 諶 偉 嚴仁軍 邱 嶼

(武漢理工大學船海與能源動力工程學院1) 武漢 430063) (高性能船舶技術教育部重點實驗室(武漢理工大學)2) 武漢 430063)

0 引 言

十字形焊接接頭廣泛應用于海洋平臺、船舶和橋梁中.隨著鋼結構薄板需求的增加，歐洲造船廠正在考慮減少游輪上部結構的結構重量，設計并使用超出船級社限制的更薄的甲板[1].然而焊接熱輸出引起的復雜輕型結構的變形已成為造船企業實現低成本制造的主要障礙，高強度薄鋼材料的使用降低了上層甲板的重量，增強了承載能力，改善了結構性能和船舶穩定性，但增加了結構焊接初始變形的傾向[2].在大型薄板焊接結構中，制造引起的初始變形給薄板的切口應力場分析和疲勞強度評估帶來了新的挑戰.

初始焊接變形給薄板結構的應力場分析和疲勞評估帶來的挑戰主要體現在兩個方面.一方面，薄板彎曲剛度較低，由焊接引起的變形不僅較之厚板要大，而且形狀呈曲線[3]，會在焊趾處產生較大的應力集中，而傳統的規范[4-6]推薦的計算焊趾處應力放大系數km值的公式均未考慮焊接初始變形的影響.為探討焊接初始變形對薄板焊接接頭焊趾處應力放大系數的影響程度，文獻[7]引入局部角變形參量αL來量化薄板對接接頭的初始變形，并對一系列考慮焊接初始變形的對接接頭試件進行了試驗.研究發現：薄板的矯直效果受試樣的長細比和實際彎曲形狀的影響很大；考慮初始變形，薄板的應力放大系數隨著應力的增加在一定程度上得到緩解，但是應力集中現象更為突出.在此基礎上，Shen等[8]對考慮初始變形的薄板對接接頭進行了研究，將非線性有限元計算結果與規范公式計算結果對比發現：對于不考慮初始變形的薄板而言，規范公式與有限元計算結果較為吻合，但當局部角變形(初始變形)逐漸增大時，規范公式與有限元計算結果之間的誤差也逐漸增大，該結論表明規范公式對于含初始變形的薄板接頭應力場評估一定的局限性，且初始變形的存在會嚴重影響焊趾處的應力放大系數.

另一個挑戰來自于薄板焊接接頭疲勞評估的復雜性.文獻[5]通過一系列實驗研究發現焊接對船用薄板結構的疲勞壽命有明顯的不利影響，主要是由于薄壁結構的疲勞強度對制造和裝配引起的缺陷比較敏感[9]，微小的焊接缺陷也會對薄板焊接結構的疲勞強度產生較大的影響[10].而且與厚板相比，薄板焊接接頭的疲勞實驗數據離散性更大，因此，薄板焊接結構在疲勞強度評估中需要使用局部方法，如結構應力方法或切口應力方法.Sonsino等[11]基于切口應力方法對一系列薄板焊接接頭的實驗數據進行了疲勞評估，發現薄板焊接接頭的疲勞壽命S-N曲線斜率的負倒數為5，比規范推薦值3要大.

綜上所述，在進行薄板焊接結構的應力場和疲勞評估時必須考慮初始焊接變形和幾何非線性的影響[12].因此，在薄板對接接頭焊趾處的應力集中系數公式的基礎上，文中針對十字形焊接接頭，對文獻[13]提出的公式進行了修正，使其適用于計算含初始變形的十字形加筋結構焊趾處的應力放大系數.將傳統規范公式計算結果、非線性有限元計算結果以及本文修正公式的計算結果進行了對比，并結合切口應力方法，運用修正公式對一系列含初始焊接缺陷的十字形接頭試件進行了疲勞評估，以此來驗證修正公式對十字形試件焊趾處應力放大系數公式計算和疲勞性能評估的準確性.

1 應力放大系數公式推導

1.1 規范公式

切口應力方法是一種基于線彈性理論的局部應力方法，除了能考慮試件幾何尺寸和焊縫幾何形狀的影響外，還可以考慮焊接錯位和焊接變形的影響.切口應力可在名義應力的基礎上乘以應力放大系數得到.

K=σnotch/σnom=kg·kw·km

(1)

式中：kg、kw為幾何形狀和幾何尺寸的應力集中系數，kw·kg=0.9+0.9(tanα)0.25；km為考慮焊接錯位和焊接角變形的應力集中系數，km=kte·ktα；其中：kte為焊接錯位引起的應力集中系數；ktα為焊接角變形引起的應力集中系數.

在十字形焊接接頭中，焊接熱輸入會使焊接試件產生明顯的焊接角變形，見圖1.

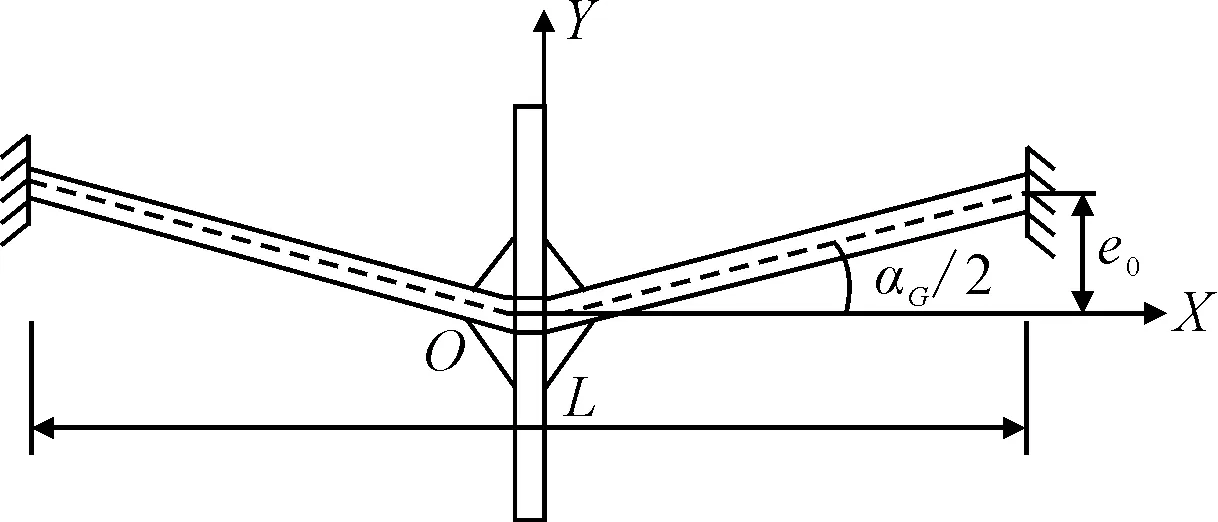
圖1 厚板十字形焊接接頭

對于無初始變形的厚板焊接試件，文獻[10]給出了由焊接角變形αG引起的焊趾處的應力集中系數ktα表達式為

(2)

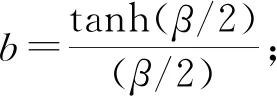
1.2 薄板焊接接頭

規范給出的應力放大系數計算公式僅適用于無初始變形的厚板焊接接頭，對于板厚小于5 mm的薄板而言，由于彎曲剛度較低，除了焊接錯位和整體角度變形外，薄板焊接結構在焊接過程中還會伴隨初始變形的出現，見圖2.文獻[6]首先引入參數對初始變形進行了量化，并對考慮初始變形的對接接頭研究發現：初始變形對焊接試件焊趾處的應力放大系數存在影響，隨著初始變形的增加，應力放大系數也會隨之增加，但當前的規范公式在計算焊趾處的應力放大系數時未考慮初始變形的影響，在求解薄板焊接接頭焊趾處的應力放大系數和進行疲勞評估時會帶來較大的誤差.因此本文綜合考慮如圖2所示的焊接整體角變形和初始變形的影響，對薄板焊接十字形試件焊趾處的應力集中系數進行了推導.

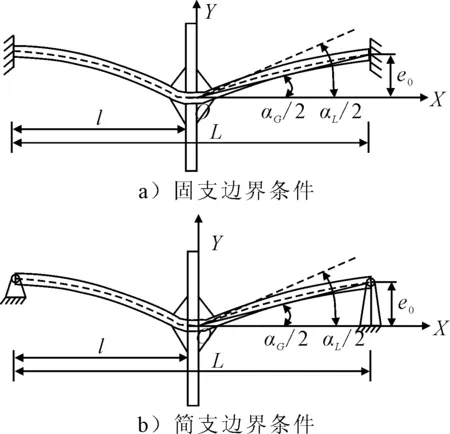
圖2 考慮初始變形的薄板十字形焊接接頭

假設試件無外力作用時的變形為，有拉伸荷載作用而引起的變形為，總變形為，則有ym=y0+y.

以十字形接頭肘板與主板的交點為坐標原點，選取圖3的力學模型進行分析，根據力和彎曲的平衡可得dV/dx=0：

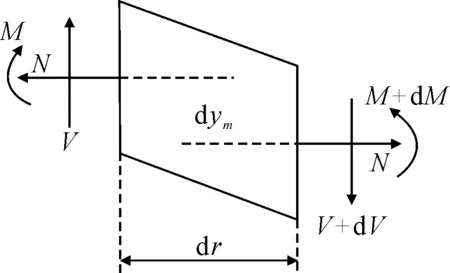
圖3 薄板十字形接頭中的微觀力學模型

(3)

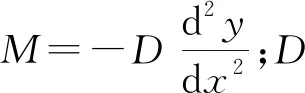
引入量綱-的量參數:

(4)

式中：e0試件約束端距橫坐標的距離.

聯立式(3)～(4)并考慮對稱情況可得：

(5)

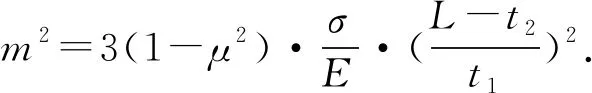
(6)

(7)

式(5)的通解為計算角變形和初始變形引起的應力放大系數的關鍵，為使式(5)具有可解性，將無荷載作用時板的曲線方程簡化為二次函數，可得η0為關于橫坐標x的方程為

η0=(1-C)ξ2+Cξ

(8)

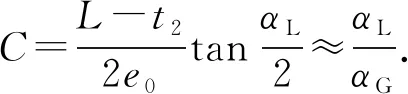
將式(8)帶入式(5)得方程的通解為

ζ=C1-Cξ+C2exp(-mξ)+

C3exp(mξ)+(C-1)ξ2

(9)

在固支邊界條件下,

(10)

在固支邊界條件下，即可得彎曲附近應力系數.

(11)

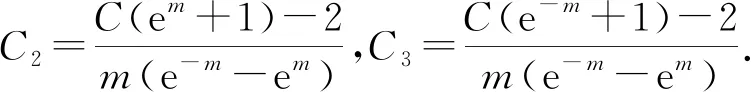
2 數值分析

2.1 試件幾何參數

為了考慮初始變形對應力放大系數的影響，運用有限元計算軟件Ansys 16.0對圖4的板厚為4 mm的一系列薄板十字形焊接試件進行了計算，試件各尺寸參數見表1.材料彈性模量為2.1×105MPa，泊松比為0.3.

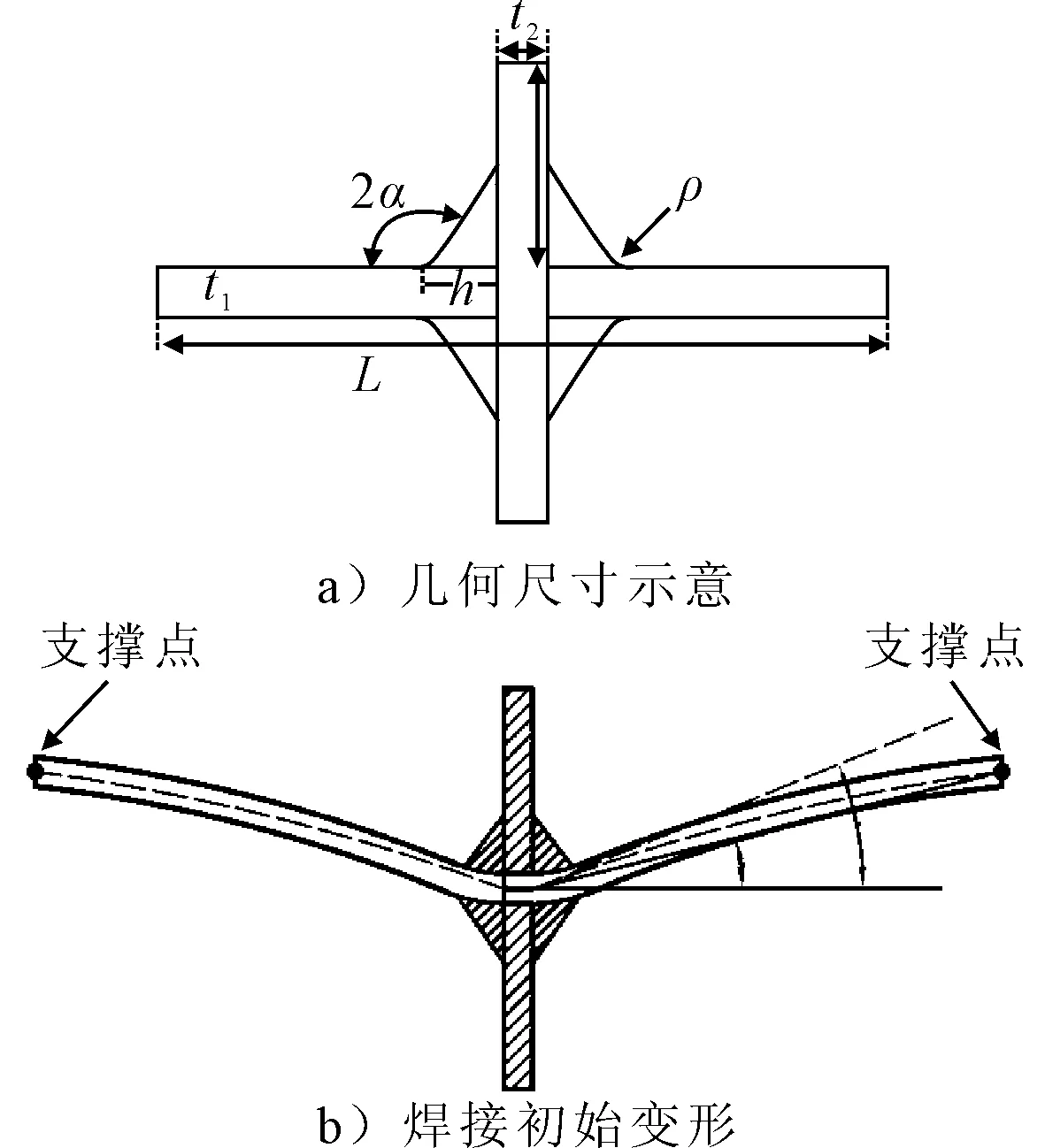
圖4 十字字型焊接接頭

表1 焊接接頭的幾何尺寸取值

2.2 有限元分析

考慮焊接角變形，可通過非線性有限元方法計算初始變形引起的應力放大系數，由于焊接接頭焊趾處的實際半徑約為1 mm，因此在有限元建模中，焊趾處的虛擬半徑取值為1 mm，并采用Solid 186單元建立了十字形試件的有限元模型，見圖6a).同時，分別考慮簡支邊界和固定邊界，數值方法中的應力放大系數可以表示為

σnotch=km·kw·σnom=kw·σHS

(12)

式中：km=σHS/σnom，σHS為熱點應力，通過線性差值得到.

為提高有限元計算結果的計算精度，首先開展網格收斂性分析.以整體角變形αG=4°,αL/αG=2，且受100 MPa均布荷載和固支邊界條件作用的十字形試件為例，圖5b)為焊趾處不同單元大小對應的從焊趾沿x方向節點的軸向應力分布圖.由圖5b)可知，當焊趾處的單元的大小為0.1 mm時，焊趾附近的應力場不再發生改變，因此本文焊趾處的單元大小取值為0.05 mm，同時該值也小于文獻[10]規定的最小單元大小ρ/4=0.25 mm.

圖5 單元收斂性分析

通過改變結構角變形比例αL/αG，可由非線性有限元方法計算得到不同幾何尺寸下十字形節點的熱點應力及應力放大系數.以名義應力αnom=50 MPa時的應力結果作為參考，圖6分別為αL/αG=1和αL/αG=4時固支和簡支兩種邊界條件下x方向的應力結果對比.由應力對比結果可知：在αL/αG=1時，固支邊界條件與簡支邊界條件下的x方向應力相差較大，隨著角變形比例αL/αG的增加，兩種邊界條件下的x方向應力場分布趨于一致，主要原因是：荷載值越大，在相同應力增量下引起的矯直效果越弱；而且隨著角變形比例αL/αG的增加，焊趾處的應力結果也會隨之增加.因此，薄板十字形接頭的初始變形對焊趾處的應力集中效應有較大影響，有必要考慮薄板初始變形對焊趾處應力放大系數的影響.

圖6 十字形試件沿x方向的應力場分布

2.3 修正公式的誤差分析

2.3.1αL=αG

為考慮薄板初始變形的影響，本文對焊趾處的應力放大系數公式進行了推導(以下統稱為修正公式).當無初始變形時，規范公式能準確的計算由焊接角變形引起的焊趾處的應力放大系數.為驗證本文修正公式(7)對于計算無初始變形試件應力放大系數的準確性，將有限元計算結果、規范公式(2)和修正公式(7)的計算結果進行對比，見圖7.由圖7可知，在不考慮初始變形時，三種方法的計算結果均比較相近，規范公式(2)和修正公式(7)與有限元計算結果之間的誤差均在10%以內.

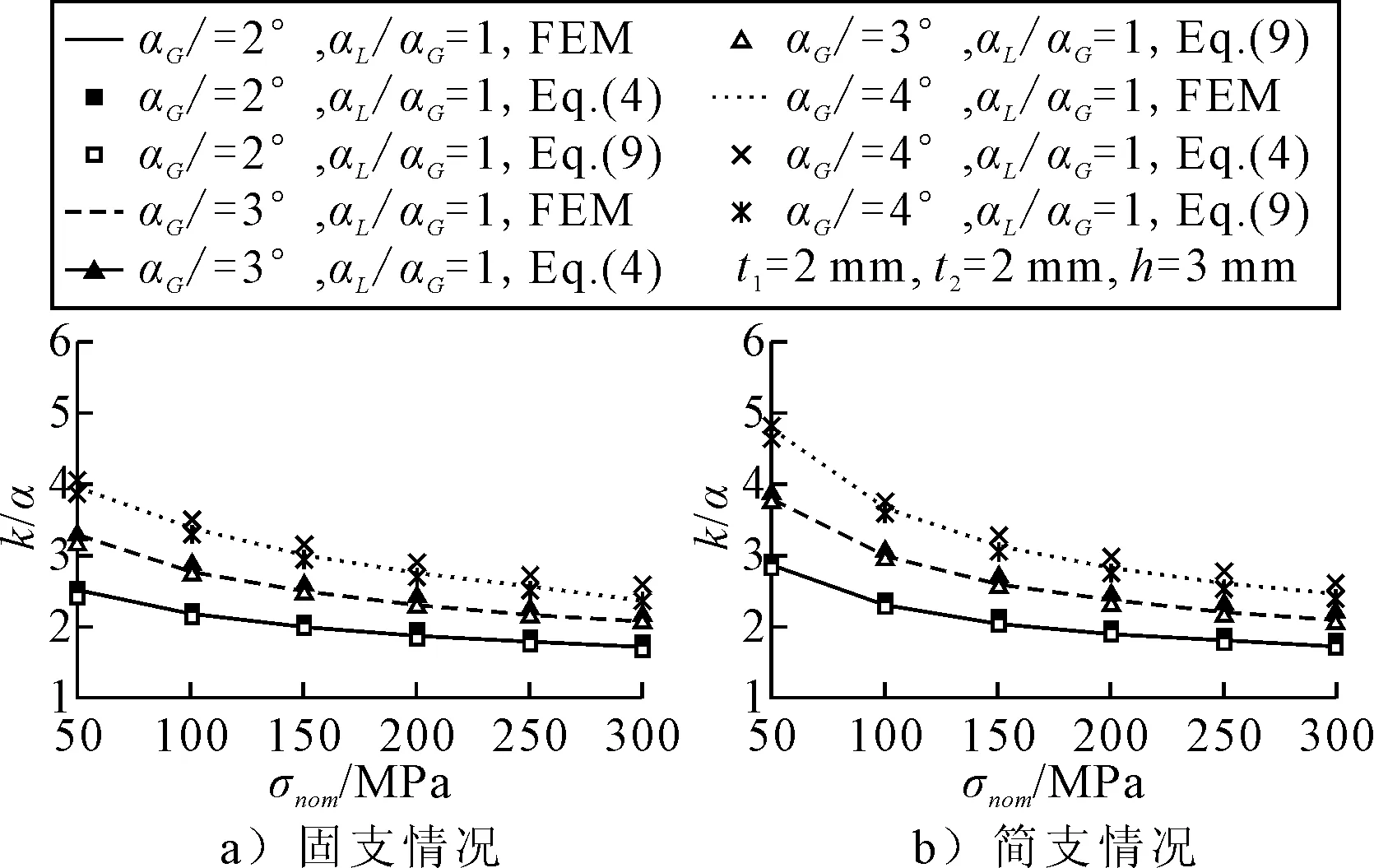
圖7 公式計算結果與有限元計算結果對比

2.3.2αL≠αG

傳統規范公式(2)在進行焊趾處的應力放大系數求解時未考慮初始變形αL的影響，而研究表明，初始變形會對焊趾處的應力放大系數產生較大的影響.本文以固支情況下的試件作為例，分別運用有限元方法和規范公式(2)對不同角變形下試件焊趾處的應力放大系數進行了計算，結果見圖8.由圖8可知，考慮初始變形時，規范公式(2)的計算結果與有限元計算結果之間誤差較大；當αL/αG=4時，規范公式(2)的計算結果與有限元計算結果之間的誤差基本上在30%以上，隨著角變形比例αL/αG的增大誤差會越來越大.

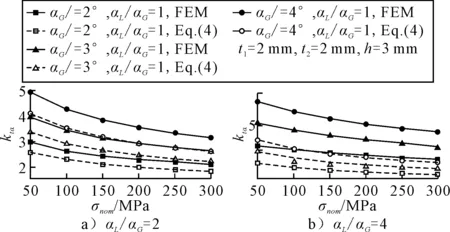
圖8 有限元方法與規范公式計算的ktα對比

為驗證本文公式的準確性，將αL≠αG時的有限元計算結果與公式(9)計算結果進行對比，見圖9.考慮不同角變形比例αL/αG，本文公式計算得到的十字形焊接試件焊趾處應力放大系數與有限元計算結果比較相近，誤差均在10%以內，因此，本文公式可以有效考慮初始變形對薄板十字形試件焊趾處應力放大系數的影響.

圖9 修正公式與有限元計算結果對比

3 疲勞強度評估

為驗證本文公式對含缺陷薄板焊接接頭的疲勞性能，基于切口應力方法，將本文修正公式(7)推廣到各類典型接頭：T形接頭、十字形接頭和對接接頭.選取一系列薄板試件的疲勞數據開展薄板結構切口應力場和疲勞評估.試件厚度為3～5 mm，彈性模量E=2.1×105MPa，泊松比μ=0.3，具體材料及尺寸參數見文獻[14].

圖10為分別運用名義應力方法、傳統規范公式和基于本文修正公式的切口應力方法的疲勞評估S-N曲線，由圖10可知，基于本文修正公式的切口應力方法得到的分散帶指數Tσ=2.26要明顯小于名義應力(Tσ=2.66)和傳統公式結果(Tσ=2.44).在考慮初始變形的情況下，運用修正公式(7)來更能有效的評估薄板焊接接頭的疲勞強度.

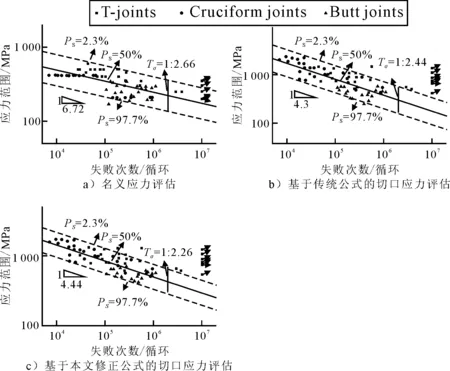
圖10 薄板焊接接頭的疲勞強度評估

基于修正公式(7)得到存活率50%時對應的S-N曲線為

lgN=18.00-4.44lgS

(13)

在疲勞壽命Nref=2×106次對應的疲勞強度為433.84 MPa，曲線斜率的負倒數為m=4.44，與文獻[14]得到的5較為接近，驗證了本文修正公式的有效性.

4 結 論

1) 文中考慮初始焊接變形，對十字形焊接試件焊趾處的應力集中系數公式進行了推導并將其運用到焊接試件的疲勞評估中.對比發現：該修正公式考慮初始變形的影響，對于不同角變形比例αg/αL的試件，本文修正公式均能準確地計算十字形試件焊趾處的應力放大系數，其計算結果與有限元計算結果之間的誤差均在10%以內，滿足工程實際的誤差要求.

2) 運用文中修正公式，在對不含初始變形的厚板焊接試件和考慮初始變形的薄板焊接試件進行疲勞評估時能有效的降低疲勞評估的分散帶指數.相比名義應力評估結果，薄板試件的切口應力S-N曲線的分散帶指數從2.66減小至2.26，可以有效提高薄板焊接結構的切口應力場和疲勞評估精度.