基于SEIRD-GEOCA的COVID-19疫情時空分布模型構(gòu)建與情景模擬

荊磊，劉明皓，陳春，曹逸凡，劉天林

1. 重慶郵電大學(xué) 計算機科學(xué)與技術(shù)學(xué)院，重慶 400065；2. 重慶郵電大學(xué) 空間信息研究中心，重慶 400065；3. 重慶交通大學(xué) 建筑與城市規(guī)劃學(xué)院，重慶 400074；4. 重慶交通大學(xué) 生態(tài)人居與綠色交通研究中心，重慶 400074

新型冠狀病毒肺炎(Corona Virus Disease 2019，COVID-19)的快速傳播，對全球政治、經(jīng)濟和社會造成了嚴(yán)重危害[1].傳染病的傳播是個復(fù)雜的時空擴散過程，對傳染病擴散建模有助于理解傳染病的傳播機理與內(nèi)在規(guī)律[2].學(xué)術(shù)界針對COVID-19傳播進(jìn)行了大量的模擬研究，但如何通過模型的構(gòu)建揭示傳染病的傳播機制，提高對疫情傳播的時空預(yù)測預(yù)警能力仍面臨很大挑戰(zhàn).目前數(shù)量預(yù)測模型主要有傳染病動力學(xué)模型，這類模型根據(jù)人群的S，E，I，R狀態(tài)分為多個倉室[S，E，I，R分別表示易感者(susceptible)、接觸者(exposed)、感染者(infected)、康復(fù)人群(removed)]，采用微分方程刻畫人群數(shù)量的變化，主要用來預(yù)測疫情的拐點和規(guī)模.依據(jù)病原體、傳染性、感染后免疫、傳染源、傳播途徑、易感人群等流行病學(xué)特征，傳染病動力學(xué)模型又可分為SI，SIS，SIR，SEIR等基本模型，分別適用于感染者不可恢復(fù)和治愈[3]、感染者治愈后可能反復(fù)感染[4]、感染者具有免疫力但潛伏期短且癥狀強烈[5]以及具有強免疫力但潛伏期較長[6]這4種情況.根據(jù)COVID-19的流行病學(xué)特征(人傳人、癥狀前傳播、呼吸道吸出物、飛沫、接觸物和糞便傳播、易感者與年齡或性別無關(guān)、感染后免疫等)，目前揭示COVID-19傳播機理的動力學(xué)模型研究仍然以SEIR模型為主[7].數(shù)量預(yù)測方面，傳統(tǒng)數(shù)學(xué)模型主要考慮參數(shù)如何準(zhǔn)確地獲取，而機器學(xué)習(xí)主要考慮驅(qū)動因子的相關(guān)性，另外，發(fā)揮不同時間序列模型優(yōu)勢的數(shù)量預(yù)測整合模型也相繼被開發(fā)出來[8].除了數(shù)量預(yù)測，揭示傳染病在空間上的擴散規(guī)律與機理也是模型研究的重要方向，這類模型主要包括多智能體[9]、CA模型等.SEIRD-agent模型用來模擬人類活動(如人為干預(yù)措施)對COVID-19疫情防控的效果[10-11].元胞自動機(Cellular Automata，CA)是一種時間、空間、狀態(tài)都離散，空間相互作用和時間因果關(guān)系為局部的網(wǎng)格動力學(xué)模型[12-16].近年來，CA與傳染病預(yù)測模型相結(jié)合被廣泛應(yīng)用于傳染病傳播的模擬研究中[17-18].Almuzakki等[19]利用SEIR-CA模型模擬疫情在人群中的傳播方式和疫苗接種策略對傳播方式的影響；Cissé等[20]利用SEIR-CA模型證明鄰近元胞的空間分布對疾病傳播的實際影響；Medrek等[21]利用SEIR-CA模型模擬柵格與人數(shù)的對應(yīng)關(guān)系，但并沒有反映前一日感染者對后一日感染者的迭代過程；Gwizdaa[22]利用SEIR-CA從個體行為對群體的影響出發(fā)，利用網(wǎng)絡(luò)中鄰居之間接觸人數(shù)的變化對干預(yù)措施進(jìn)行分析.

歸納起來，目前對于傳染病的數(shù)量預(yù)測、聚集特征與擴散機制的模型構(gòu)建主要集中在以下兩方面.一是從傳染病的傳統(tǒng)模型出發(fā)，對一定統(tǒng)計區(qū)域的傳染病人數(shù)進(jìn)行推估，較少考慮細(xì)粒度的空間交互，如SEIR模型，這類模型盡管有較好的時間分辨率，但空間分辨率很差；二是從CA出發(fā)，CA模型盡可能地將研究區(qū)域劃分為較小的格網(wǎng)來模擬傳染病在不同情景下的空間擴散情況.在一定程度上揭示了流行機理與內(nèi)在規(guī)律，但大多數(shù)研究沒有將傳染病的擴散與生物生存環(huán)境的地理相似性有效結(jié)合起來，不具有真正的生物地理學(xué)意義，本質(zhì)上是一種數(shù)值仿真模擬.鑒于其在模擬復(fù)雜系統(tǒng)時強大的時空演變過程能力，通過與機器學(xué)習(xí)和人工智能等算法的結(jié)合，構(gòu)建高時空分辨率的耦合模型，是傳染病傳播模型需進(jìn)一步探討的方向.另外，傳染病的空間擴散，既存在空間上隨距離衰減的連續(xù)蔓延的擴散方式，也存在從高級節(jié)點向低級節(jié)點城市滲透的空間跳躍式等級擴散方式[23-24].傳染病的擴散與蔓延是在一定時間、空間尺度上的傳播過程，其時空關(guān)系相互依存、不可分割[25-26].相關(guān)研究也發(fā)現(xiàn)傳染病感染者不僅具有很強的時間關(guān)聯(lián)性，而且感染者的空間分布與其生活的其他空間屬性也具有強相關(guān)性[27-30]，因此構(gòu)建時空耦合模型，并將上述空間擴散機制融入傳染病擴散模型中用來揭示傳染病的空間傳播機制具有十分重要的理論和實踐意義.

本研究①為充分發(fā)揮SEIR模型和CA模型在時間分辨率預(yù)測和空間分辨率仿真方面的優(yōu)勢，依據(jù)空間現(xiàn)象地理相似性原理，構(gòu)建了一種基于SEIRD-GEOCA的傳染病時空耦合模型；②在模型中融入接觸擴散和隨機遷移擴散策略，采用重慶市感染者軌跡數(shù)據(jù)和統(tǒng)計數(shù)據(jù)實現(xiàn)對重慶市COVID-19疫情時空分布的情景模擬和預(yù)測，揭示COVID-19疫情的時空擴散規(guī)律和傳播機理；③實現(xiàn)不同感染源與干預(yù)情景下的時空擴散模擬與效應(yīng)評估.

1 模型構(gòu)建原理與方法

本研究構(gòu)建了SEIRD-GEOCA時空耦合模型用于模擬COVID-19疫情的時空擴散規(guī)律，該模型包括數(shù)量預(yù)測模塊、空間映射模塊和時空耦合模塊.數(shù)量預(yù)測模塊在經(jīng)典的SEIR模型基礎(chǔ)上引入了有無封城的情景，用來表示隨著時間變化新增的感染者數(shù)量；空間映射模塊利用CA模型將感染者分配到空間柵格上，將感染源分為本地潛在感染源和外部輸入感染源，加入了有無排查政策；時空耦合模塊將前2部分進(jìn)行整合，實現(xiàn)每日疫情地圖的動態(tài)迭代.空間適宜性概率充分考慮地理相似性原理，即某種傳染病病毒的傳播和生存與”生物島”的大小、島與島的關(guān)聯(lián)性、自然環(huán)境與文化環(huán)境的相似性等密切相關(guān).

1.1 SEIRD模塊

經(jīng)典SEIR模型將人群分為易感人群、接觸人群、感染人群和康復(fù)人群，但不能很好地表現(xiàn)政府干預(yù)措施的影響.該模型假設(shè)人群中所有個體都有被感染的概率，當(dāng)被感染個體痊愈后，會產(chǎn)生抗體.考慮到防治傳染病的隔離措施，在傳統(tǒng)SEIR模型上，將R細(xì)分為R和D，并調(diào)整封城前后每人每天接觸的人數(shù)，形成新的傳染病動力學(xué)模型SEIRD模型[7].

如圖1中SEIRD模型所示，S，E，I，R，D分別表示易感人群、接觸人群、感染人群、康復(fù)人群(治愈人群)、死亡人群；α代表每人每天接觸的人數(shù)，β代表被感染的概率，α×β代表感染力；σ代表E轉(zhuǎn)為I的概率；γ代表I轉(zhuǎn)為R的概率(治愈率)；κ代表I轉(zhuǎn)為D的概率(致死率).

SEIRD模型如下所示：

(1)

式中：St代表t時刻易感人數(shù)，對應(yīng)統(tǒng)計數(shù)據(jù)中的健康人數(shù)，S=N-E-I-R-D；Et代表t時刻接觸人數(shù)，對應(yīng)統(tǒng)計數(shù)據(jù)中的新增疑似人數(shù)；It代表t時刻感染人數(shù)，對應(yīng)統(tǒng)計數(shù)據(jù)中的新增確診人數(shù)；Rt代表t時刻治愈人數(shù)，對應(yīng)統(tǒng)計數(shù)據(jù)中的累計治愈人數(shù)；Dt代表t時刻死亡人數(shù)，對應(yīng)統(tǒng)計數(shù)據(jù)中的累計死亡人數(shù)；N代表總?cè)丝跀?shù)，對應(yīng)研究區(qū)域內(nèi)的總?cè)丝跀?shù)；t代表時間；α代表每人每天接觸的人數(shù)，與防控政策有關(guān).封城隔離前，α=15，封城隔離后，α=3[6]；β1代表感染人群的感染率；β2代表潛伏人群的感染率；σ代表潛伏人群(E)轉(zhuǎn)為感染人群(I)的概率；γ代表感染人群(I)轉(zhuǎn)為治愈人群(R)的概率(即治愈率)；κ代表感染人群(I)轉(zhuǎn)為死亡人群(D)的概率(即致死率).

1.2 地理相似性原理與GEOCA模塊構(gòu)建

GEOCA模塊將研究區(qū)域劃分為若干個均質(zhì)空間.為了簡化計算，GEOCA狀態(tài)設(shè)置為感染與非感染2種狀態(tài)，其中感染格網(wǎng)還記錄該格網(wǎng)在病毒生命周期范圍內(nèi)(7 d)感染者的累計數(shù)量.格網(wǎng)轉(zhuǎn)換規(guī)則最終受全局影響因素(如適宜性、約束性和隨機性)和局部影響因素(如鄰域)的影響.通過建立影響疾病傳播的空間驅(qū)動因子與疾病分布的相關(guān)關(guān)系，借助機器學(xué)習(xí)等相關(guān)算法，學(xué)習(xí)觀測時段內(nèi)某傳染性疾病在不同空間位置發(fā)生的概率，形成傳染性疾病的空間適宜性概率地圖.同時通過整合傳染性疾病的空間適宜性、約束性概率、鄰域概率和隨機概率等形成綜合概率.GEOCA模塊中如何完成新增患者數(shù)量的空間配置十分關(guān)鍵.本研究采用2種策略(蔓延擴散策略和隨機遷移擴散策略)完成新增傳染性疾病個體的空間配置.蔓延擴散策略依據(jù)傳染鄰域概率的高低來完成新增傳染者個體的空間配置.隨機遷移擴散策略依據(jù)某格網(wǎng)空間綜合概率越高，新增傳染性疾病的個體映射到該格網(wǎng)空間的可能性越大的原則完成新增傳染者個體的空間配置.根據(jù)地理學(xué)第三定律，地理環(huán)境越相似，在該環(huán)境中地理個體的目標(biāo)特征相近的概率越大.借助地理相似性原理可判斷某區(qū)域與感染區(qū)域是否具有相似的環(huán)境特征，一旦種子點落入該環(huán)境，則該區(qū)域傳染該病毒的可能性也比較大.可通過機器學(xué)習(xí)方法獲得觀測期間新冠病毒的空間適宜性(見圖1).

CA模型中每個元胞的總體轉(zhuǎn)換概率取決于疫情發(fā)展的適宜性Ps、鄰域效應(yīng)Ω與限制因素Pc.疫情發(fā)展的適宜性通過隨機森林算法計算得到.隨機森林利用多棵決策樹對樣本進(jìn)行訓(xùn)練預(yù)測，可用于回歸和分類預(yù)測算法中，屬于集成學(xué)習(xí)的bagging算法[24-25]，如式(2)所示.

(2)

(3)

在疫情擴張模擬研究中，非感染元胞i在時刻t轉(zhuǎn)換為感染元胞的概率可表示為

(4)

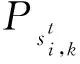
鄰域效應(yīng)是CA模型的重要組成部分，代表n×n鄰域范圍內(nèi)的中心元胞與周邊元胞的相互作用.具體表現(xiàn)為中心元胞n×n鄰域范圍內(nèi)感染元胞的密度.元胞i在時刻t的鄰域效應(yīng)可表示為

(5)

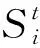
限制因素約束了特殊區(qū)域向感染者所在柵格的轉(zhuǎn)換.在實際疫情擴張過程中，考慮到地理和政策因素，諸如水體和無人區(qū)等不會轉(zhuǎn)變?yōu)楦腥緰鸥?限制因素可表示為

(6)

其中，LUk表示第k種土地利用類型；當(dāng)元胞i在時刻t滿足擴張約束條件時，con()取值為1，否則取值為0.本研究對河流、湖泊、無人區(qū)進(jìn)行限制，規(guī)定其不會轉(zhuǎn)換為城市.

因此，元胞i在時刻t的總體轉(zhuǎn)換概率可表示為

(7)

CA模型的最終停止條件為

(8)

其中，A代表將新增加的n個感染者分配到空間柵格的疫情地圖圖層.Ai代表第i個感染者所在元胞的位置.

1.3 時空耦合模塊

本研究利用CA模型的動態(tài)演化特征，將CA模型用于新型冠狀病毒感染者的空間分布模擬中，充分發(fā)掘其空間動態(tài)演化規(guī)則.SEIRD模型產(chǎn)生每日感染者的數(shù)量，CA模型分配感染者.時空耦合模塊通過構(gòu)建約束函數(shù)將上述2種模型耦合，形成CA迭代與轉(zhuǎn)換規(guī)則，完成模型的運算(見圖1).

時空耦合模型的最終停止條件可表示為

(9)

其中，A代表預(yù)測期間累計n天時間范圍內(nèi)待分配感染者最終被分配的疫情地圖圖層；Aij代表第i天第j個感染者所在元胞的位置.

2 數(shù)據(jù)來源和處理

重慶市位于中國西南部，地跨東經(jīng) 105°11′～110°11′、北緯 28°10′～32°13′，是青藏高原與長江中下游平原的過渡地帶.東鄰湖北、湖南，南靠貴州，西接四川，北連陜西，總面積約 8.24萬平方千米，轄26個市，8個縣，4個自治縣.重慶市鄰近湖北，與湖北人員來往頻繁，受COVID-19疫情影響較大.疫情期間，重慶市先后設(shè)立新型冠狀病毒肺炎治療定點醫(yī)院48個，故選擇重慶作為研究區(qū)域.

圖片來源于國家基礎(chǔ)地理信息中心標(biāo)準(zhǔn)地圖服務(wù)網(wǎng)站“中國分省地圖—重慶市”，審圖號為GS(2019)3333.圖2 研究區(qū)域示意圖

2.1 數(shù)據(jù)來源

COVID-19疫情數(shù)據(jù)主要來自國家衛(wèi)生健康委員會官網(wǎng)(http：//www.nhc.gov.cn/)、世界衛(wèi)生組織(https：//www.who.int/westernpacific)、MIDAS network等官方公布的統(tǒng)計數(shù)據(jù).從MIDAS network的統(tǒng)計數(shù)據(jù)可看出，重慶市COVID-19疫情新增確診者主要分布在2020年1月21日至2月29日，故選取該時間段數(shù)據(jù)對重慶市COVID-19疫情進(jìn)行分析模擬預(yù)測.本研究使用的COVID-19數(shù)據(jù)包括統(tǒng)計數(shù)據(jù)和感染者軌跡數(shù)據(jù)，統(tǒng)計數(shù)據(jù)涉及新增疑似、新增確診、累計死亡、累計治愈等，數(shù)據(jù)來自美國匹茲堡大學(xué)公共衛(wèi)生研究生院公共衛(wèi)生動力學(xué)實驗室(Public Health Dynamics Lab，PHDL).感染者軌跡數(shù)據(jù)通過華龍網(wǎng)獲取.

考慮到COVID-19的傳播與人類活動密切相關(guān)，本文選取自然環(huán)境和社會經(jīng)濟2類數(shù)據(jù)作為影響其傳播的主要驅(qū)動因子(見表1).

2.2 數(shù)據(jù)處理

將表中的異構(gòu)數(shù)據(jù)統(tǒng)一研究區(qū)域范圍、空間坐標(biāo)系和分辨率.9類POI數(shù)據(jù)采用網(wǎng)絡(luò)爬蟲軟件爬取后，進(jìn)行核密度分析獲得核密度分布圖層.由于COVID-19感染者的分布與用地類型有一定的相關(guān)性，水域和無人區(qū)完全不可能出現(xiàn)COVID-19感染者，故本研究將用地類型重新分為3類，其中未利用土地和水域等無人區(qū)分為1類，耕地、林地、草地分為1類，城鄉(xiāng)居民用地分為1類.無人區(qū)作為模型構(gòu)建過程中的約束概率層.高程數(shù)據(jù)來自ASTERGDEM，分辨率為30m，經(jīng)過掩膜提取得到重慶市的高程圖層；借助ARCGIS經(jīng)過坡度計算得到坡度圖層.距河流、鐵路、高速公路、主干道、二級道路的距離數(shù)據(jù)來源于開放街道地圖(Open Street Map，OSM)，在ARCGIS中經(jīng)過歐氏距離分析得到各交通線路的歐氏距離圖層.重慶市COVID-19感染者活動軌跡數(shù)據(jù)來源于華龍網(wǎng)，首先將COVID-19感染者文本信息中涉及的小區(qū)、街道、村、鄉(xiāng)鎮(zhèn)、縣等位置數(shù)據(jù)通過網(wǎng)絡(luò)爬蟲軟件在高德地圖中爬取其對應(yīng)的帶地理坐標(biāo)的點數(shù)據(jù)，然后進(jìn)行坐標(biāo)轉(zhuǎn)換(GCJ-02→WGS-84)，從而得到不同時間COVID-19感染者的位置分布圖層.

表1 空間模型驅(qū)動因子的選擇和數(shù)據(jù)說明

3 模型實施

3.1 整合模型構(gòu)建

3.1.1 SEIRD模型構(gòu)建

采集重慶市2020.1.21-2020.2.29的COVID-19感染者統(tǒng)計數(shù)據(jù)進(jìn)行探索性分析(圖3a)，將COVID-19感染者統(tǒng)計數(shù)據(jù)和采用SEIRD模型模擬的結(jié)果進(jìn)行對比(圖3b)，從數(shù)據(jù)走勢可看出，實際數(shù)據(jù)曲線趨勢與SEIRD曲線趨勢相同，表明SEIRD模型能夠有效反映COVID-19感染者數(shù)量的發(fā)展趨勢.COVID-19存活時間為2～14 d，將平均潛伏期定為符合報道的7 d，死亡率設(shè)置為3%[6].在采取嚴(yán)格的防控措施下，感染者數(shù)量峰值顯著降低，疫情高峰更早地到來.

圖3b中，藍(lán)色曲線反映實際感染者數(shù)量隨天數(shù)的變化情況，紅色曲線代表模擬的感染者數(shù)量在有干預(yù)的情況下隨天數(shù)的變化情況.采用SEIRD模型，對重新調(diào)優(yōu)后的模擬感染者曲線進(jìn)行格網(wǎng)搜索，尋找最優(yōu)參數(shù).實驗得出，在β1為0.02，β2為0.03，σ為0.2，γ為0.29時，這條曲線擬合效果最好.

3.1.2 融入不同擴散策略的GEOCA模型構(gòu)建

1) 基于地理相似性原理的概率圖層生成

COVID-19疫情的傳播與人類活動密切相關(guān).本文選用隨機森林(利用多棵樹對樣本進(jìn)行訓(xùn)練并預(yù)測的一種分類器)算法，以重慶市為研究區(qū)域，將高程、坡度、用地類型、河流作為自然環(huán)境驅(qū)動因子，將醫(yī)院、學(xué)校、賓館、購物、餐飲、風(fēng)景名勝、娛樂場所、銀行、車站站點、鐵路、高速公路、主干道、二級道路、人口密度作為社會經(jīng)濟驅(qū)動因子，將2020年1月21日到2020年2月29日整個時間范圍內(nèi)疫情感染者的空間位置作為標(biāo)簽，進(jìn)行回歸，得到適宜性概率層(Ps)，如圖1綜合空間適宜性概率所示.

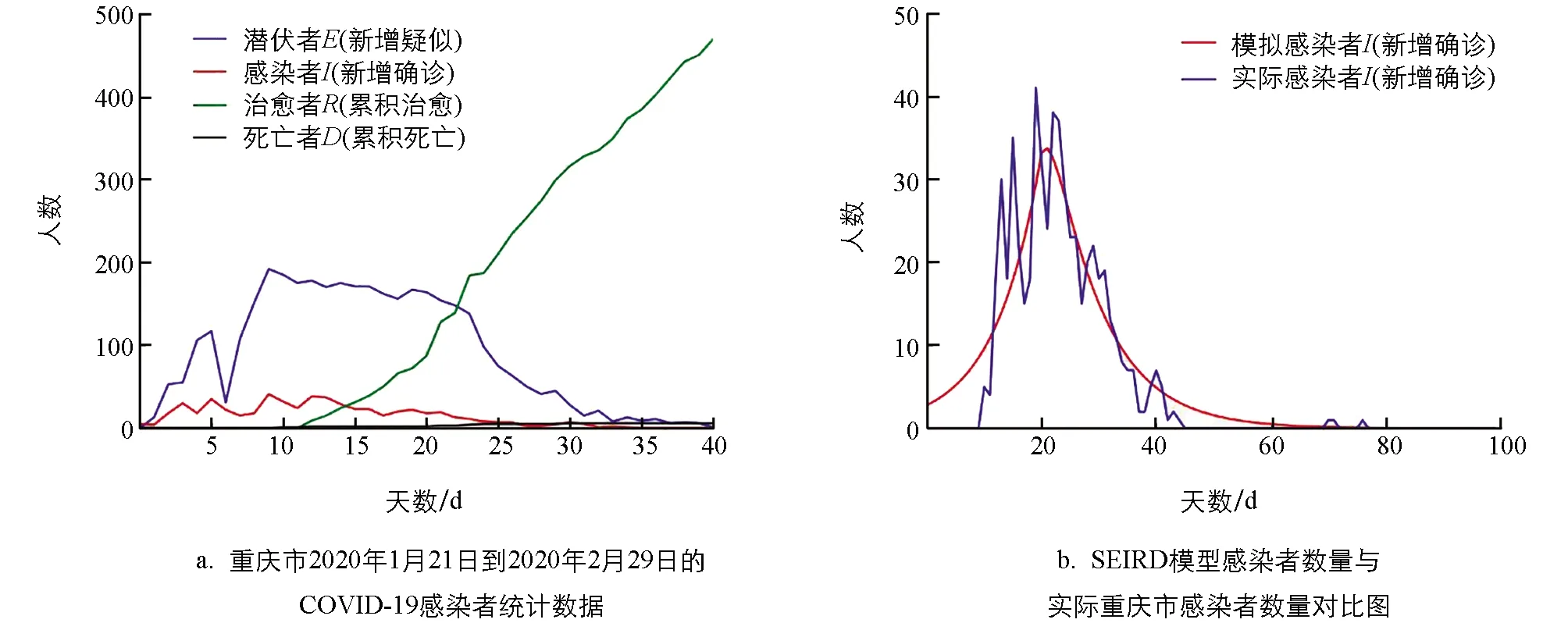
圖3 COVID-19統(tǒng)計分析與SEIRD感染者數(shù)量模擬

隨機森林可利用袋外數(shù)據(jù)計算驅(qū)動因子的重要性.各個驅(qū)動因子中銀行核密度對感染者分布影響最大，其次各種興趣點以及人口是影響疫情感染者分布的重要因素，說明社會經(jīng)濟因素對疫情感染者分布具有主要影響力.另外，高程坡度、用地類型等對感染者分布影響較弱，原因在于重慶以丘陵和山地為主，坡度面積較大，城市基本在復(fù)雜的地形地貌上進(jìn)行擴張，因此感染者的空間分布對地理環(huán)境相對不敏感.

2) 空間擴散策略的實現(xiàn)

如何將預(yù)測的新增感染者映射到某一格網(wǎng)空間，實現(xiàn)從數(shù)量預(yù)測到空間位置預(yù)測的轉(zhuǎn)變，是該時空耦合模型構(gòu)建的關(guān)鍵.空間擴散建模需模擬傳染病的2種空間擴散機制：一種是輸入型病例，另一種是在已有病例基礎(chǔ)上的接觸蔓延(“生根發(fā)芽”).本研究采用2種策略，一種是蔓延擴散策略，另一種是隨機遷移擴散策略.

① 蔓延擴散策略

在某一格網(wǎng)位置一旦發(fā)現(xiàn)有COVID-19感染者，病毒便依托已有感染者沿著交際鏈、交通鏈按一定概率在“生物島”內(nèi)近距離接觸擴散.它的傳播與人際交往、防護(hù)措施和病毒防范意識等密切相關(guān)，以聚會或親朋交往等近距離接觸傳播為主.其觀測區(qū)域是已有COVID-19感染者分布格網(wǎng)的近鄰區(qū)域.鑒于蔓延擴散以“在地型”病例或已“落地生根”的輸入型病例近距離蔓延為特征，因此預(yù)測的新增感染者位置落在何處同時受傳染周期內(nèi)已有的COVID-19感染者的位置分布和鄰域概率影響.本研究擬將已有COVID-19感染者柵格作為候選點，使得在該點鄰域范圍內(nèi)，綜合概率圖層最大者，新增感染者落在該點的可能性最大，即已有的COVID-19感染者柵格鄰域范圍內(nèi)概率大者優(yōu)先配置位置，直到新增感染者全部分配完畢，完成蔓延擴散策略(見圖1).隨機遷移擴散和蔓延擴散在時間上將同時發(fā)生.如COVID-19患者發(fā)生位置移動，則擴散方式由蔓延擴散轉(zhuǎn)變?yōu)殡S機遷移擴散.

② 隨機遷移擴散策略

因COVID-19接觸者從感染到爆發(fā)具有潛伏期，且在潛伏期已經(jīng)具有傳染性，使得病毒從源頭通過中間宿主輸入到”生物島”，在病毒爆發(fā)直至采取隔離措施之前，接觸者并不知道該病毒是什么，來自何方，去往何處.因此這里的隨機擴散是指在對病毒位置信息雙盲情形下，病毒傳播宛如“隨風(fēng)飄散的蒲公英”，蒲公英種子點到底花落何家，一切隨機(病毒的初始傳播具有很強的隨機性和危害性).隨機遷移擴散主要表現(xiàn)為通過交通鏈在“生物島”間的遠(yuǎn)距離輸入性傳播，它類似蛙跳在不同的”生物島”間跳躍性遷移擴散.隨機擴散在傳染病早期表現(xiàn)比較明顯，即使后期采取核酸檢測、禁足限行等措施，大大減少了傳播的強度，但也常有“漏網(wǎng)之魚”，如時有發(fā)生的輸入性病例就是隨機遷移擴散的表現(xiàn).

由于遠(yuǎn)距離流通形式(物流、人流)的存在，增強了種子點在“生物島”之間或島內(nèi)不確定性位置上傳播的可能性，使得采取隨機遷移擴散策略成為必要.隨機遷移擴散策略的觀測區(qū)域是整個研究區(qū)域的各“生物島”.鑒于預(yù)測的新增感染者個體可能通過輸入的方式以不同的概率進(jìn)入“生物島”的任何格網(wǎng)空間，因此本研究借助輪盤賭的思想，在COVID-19感染空間適宜性圖層上疊加隨機因子，實現(xiàn)新增感染者在空間上的隨機遷移擴散策略(見圖1).

當(dāng)然，隨著時間的推移，預(yù)測的感染者數(shù)量與位置將不斷得到糾正，通過元胞的不斷更新迭代，得到若干日的疫情分布圖層.時間越長學(xué)習(xí)的知識越充分，預(yù)測能力越強.為了實現(xiàn)一日感染者空間分布圖層，將適宜性概率層與用地類型重分類后得到的約束性概率層(Pcon)相乘得到全局概率層(Pglo)，根據(jù)前一日疫情地圖圖層，按柵格的概率選取一個感染者所在的柵格作為種子點(i，j)，即可得到該種子點在全局概率層中的綜合概率，由ROI(PROI)相乘鄰域概率層(Pnei)得到，按照柵格概率隨機選取感染柵格，重復(fù)上述過程，待當(dāng)日感染者全部分配完成后，即完成一次CA迭代.COVID-19疫情的傳播表現(xiàn)為外界輸入和繼發(fā)性蔓延機制，前者表現(xiàn)為隨機突變點，發(fā)生在疫情早期，后者表現(xiàn)為從本地種子點蔓延到周邊柵格，發(fā)生在疫情中后期.

3.1.3 時空耦合模型構(gòu)建

將SEIRD模型與GEOCA模型相結(jié)合，在封城有排查，平均潛伏期為7 d的情景下，利用前7日的感染者圖層結(jié)合第8日感染者的數(shù)目，產(chǎn)生第8日的疫情地圖圖層，依次迭代，即可得到整個時間段的疫情地圖圖層，從而完成時空耦合模型的構(gòu)建.

3.2 模型校正與檢驗

3.2.1 對比方案設(shè)計

本研究基于以下假設(shè)：

1) 使用不同的圖層(感染者核密度圖層、實際人數(shù)柵格圖層以及有無感染者的01柵格圖層)作為鄰域分析圖層，將對結(jié)果產(chǎn)生影響，且差異有統(tǒng)計學(xué)意義.

2) 模擬過程中，是否采取干預(yù)措施以及采取不同的干預(yù)措施將對結(jié)果產(chǎn)生影響且差異有統(tǒng)計學(xué)意義.

3) 將新聞報道中的2～14 d的潛伏期設(shè)為7 d.

選取2020年1月21日到2020年2月29日的COVID-19感染者統(tǒng)計數(shù)據(jù)和點數(shù)據(jù)，針對上述假設(shè)設(shè)計了5種對比方案，并分別與實際疫情地圖圖層進(jìn)行對比分析，其具體方案為：

方案一(封城有排查kernel)：采取封城有排查的干預(yù)措施，用感染者核密度圖層作為鄰域分析圖層，簡稱kernel，采用SEIRD-GEOCA模型模擬感染者時空分布.

方案二(封城有排查pop)：采取封城有排查的干預(yù)措施，用實際人數(shù)柵格分布圖層作為鄰域分析圖層，簡稱pop，采用SEIRD-GEOCA模型模擬感染者時空分布.

方案三(封城有排查01)：采取封城有排查的干預(yù)措施，用感染者01柵格分布圖層作為鄰域分析圖層，簡稱01，采用SEIRD-GEOCA模型模擬感染者時空分布.

方案四(封城無排查)：采取封城無排查的干預(yù)措施，用實際人數(shù)柵格圖層作為鄰域分析圖層，采用SEIRD-GEOCA模型模擬感染者時空分布.

方案五(無干預(yù))：不采取干預(yù)措施，用實際人數(shù)柵格圖層作為鄰域分析圖層，采用SEIRD-GEOCA模型模擬感染者時空分布.

這里的有排查是指針對疫情發(fā)展?fàn)顩r，積極采取必要的隔離(限行、禁足、集中隔離)、病例調(diào)查、紅外溫度計測溫和核酸檢測等措施.在模型中表現(xiàn)為通過調(diào)整種子點的生命周期，使得種子點在病毒潛伏期內(nèi)能感染其他人，但超過7 d，由于對種子點采取了積極的隔離和治療等措施，從而使得種子點自動消亡.無排查是指針對疫情發(fā)展?fàn)顩r，未及時采取必要的排查措施，在模型中表現(xiàn)為種子點在病毒潛伏期內(nèi)不會失活，種子點將會一直傳染他人.封城措施是指針對疫情發(fā)展?fàn)顩r，政府采取了果斷的城市封鎖政策，防止疫情在城外快速擴張.在模型中表現(xiàn)為讓種子點每天接觸的人數(shù)從無任何防護(hù)措施的情況下接觸15人/日，調(diào)整到3人/日.通過調(diào)控種子點是否消亡區(qū)分有無排查，通過調(diào)整SEIRD模型接觸人數(shù)來區(qū)分是否封城.

3.2.2 對比方案設(shè)計

分別從柵格尺度和區(qū)縣尺度，利用均方誤差(Mean Square Error，MSE)、平均絕對誤差(Mean Absolute Error，MAE)、均方根誤差(Root Mean Square Error，RMSE)對模型的精度進(jìn)行檢驗.

均方誤差是各數(shù)據(jù)偏離真實值差值平方和的平均數(shù)，也就是誤差平方和的平均數(shù)；平均絕對誤差是指觀測值與真實值的誤差絕對值的平均值；均方根誤差是指觀測值與真實值偏差的平方和與觀測次數(shù)n比值的平方根.

4 結(jié)果分析

選取重慶市2020年1月21日到2020年2月29日的感染者為研究對象，通過SEIRD-GEOCA模型得到不同情形下感染者的空間分布模擬結(jié)果，同時將不同情形下的模擬結(jié)果和真實環(huán)境下的COVID-19感染者時空分布進(jìn)行對比(表2).同時，采用核密度制圖法直觀展示模擬結(jié)果，并與觀測期間真實環(huán)境下的COVID-19感染者時空分布進(jìn)行對比(見圖4).

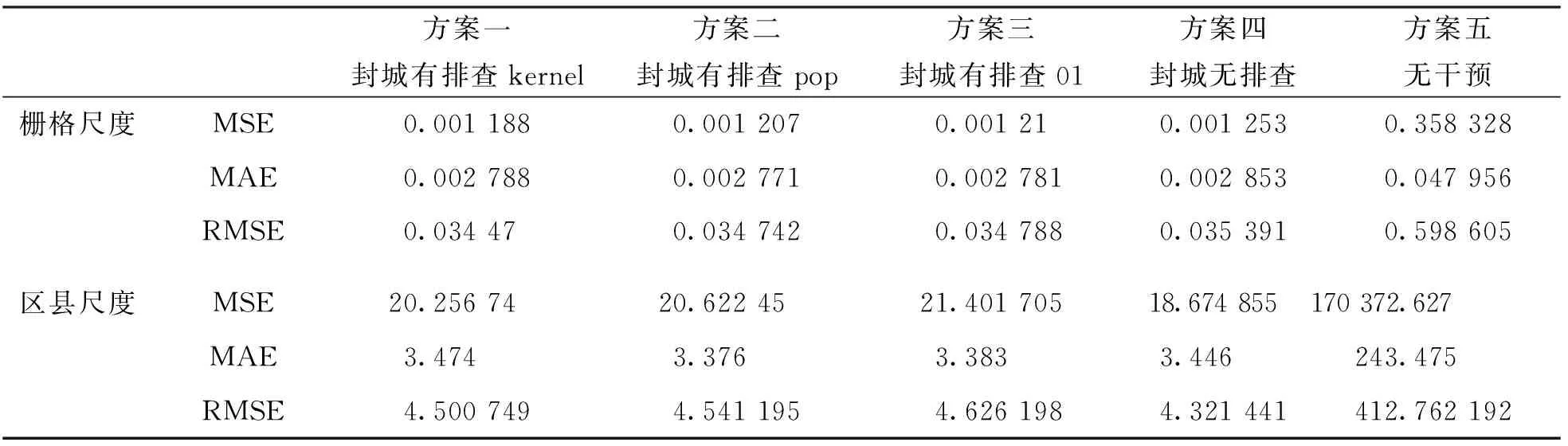
表2 不同情景模擬結(jié)果與真實情況的對比

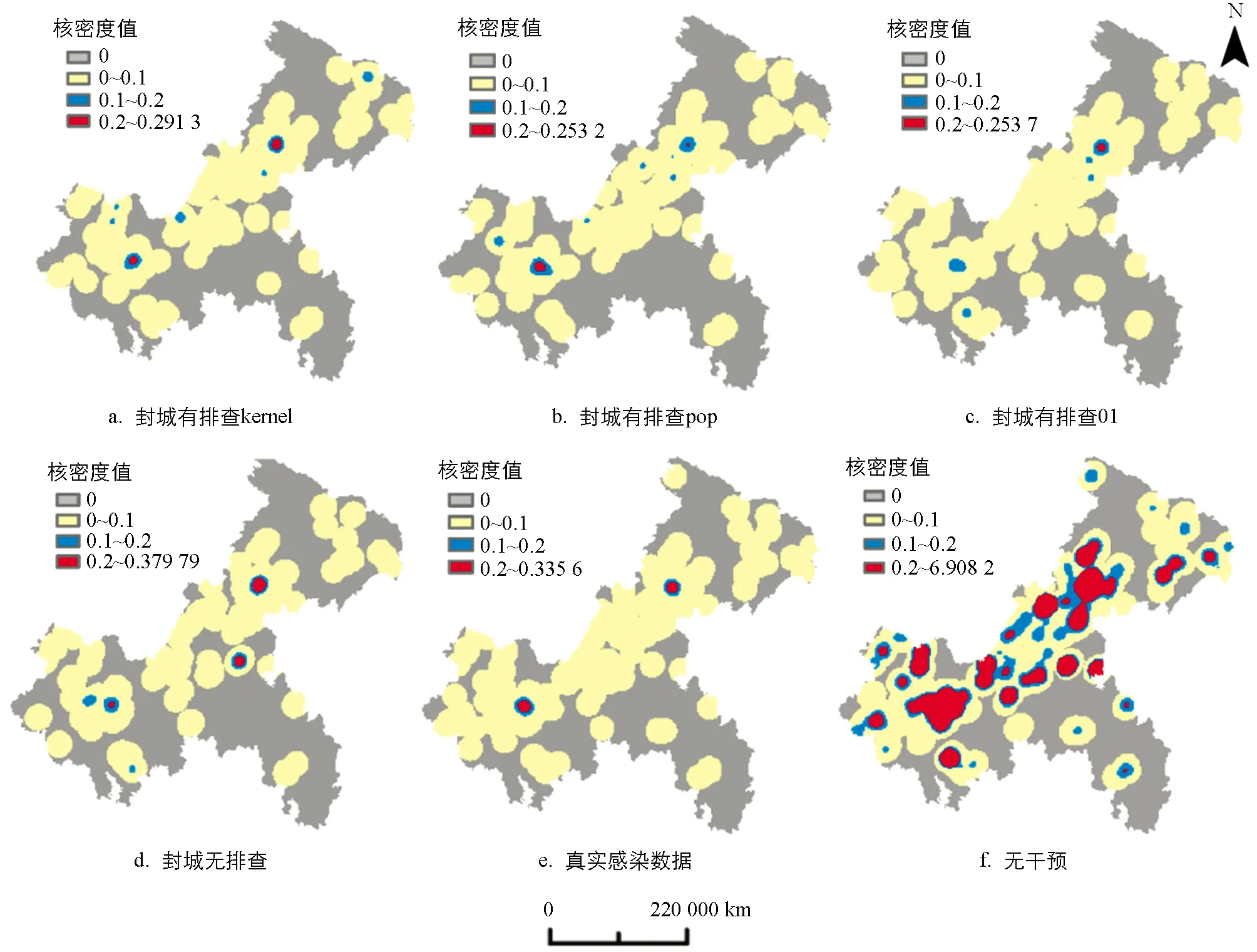
圖4 不同方案下COVID-19感染者空間分布模擬結(jié)果對比圖

方案一、二、三表明，MSE，MAE，RMSE三者差距并不顯著，且上述三類誤差的最大偏離度為5.52%.但相較于實際人數(shù)柵格圖層和有無感染者的01柵格圖層，選取感染者核密度圖層作為鄰域分析圖層能獲得更好的可視化效果(方案一)(圖4a).根據(jù)表2各項指標(biāo)可看出，方案一中各精度項指標(biāo)比其他方案稍優(yōu).方案二的擴散中心圍繞著以主城區(qū)為核心的渝西南地區(qū)，與實際情況稍有偏離(圖4b)，方案三的擴散中心則圍繞著以萬州區(qū)為核心的渝東北地區(qū)，與實際情況偏離程度最大(圖4c).因此，方案一更顯合理.方案一、四對比可看出，在封城的前提下，相較于有排查情形，無排查情形呈現(xiàn)出團簇現(xiàn)象，表明封城無排查會產(chǎn)生超級傳播者，在人口較為集中的區(qū)域傳播.方案一、五對比可看出，有無干預(yù)對COVID-19疫情空間擴散影響顯著，防控措施可有效地遏制COVID-19疫情大面積傳播.重慶重點防控區(qū)域為以萬州區(qū)為核心的渝東北地區(qū)和以主城區(qū)為核心的渝西南地區(qū).從數(shù)量來看，無干預(yù)比有干預(yù)在觀測期間里數(shù)量上要多很多倍，無干預(yù)使得局面失控，整個重慶市形成了以各區(qū)縣為中心的眾多熱點區(qū)域.

5 結(jié) 論

本研究賦予CA模型生物地理學(xué)意義，構(gòu)建了一種基于SEIRD-GEOCA的COVID-19疫情時空分布模型，在模型中融入蔓延擴散和隨機遷移擴散策略，設(shè)計了5種方案用于驗證干預(yù)措施，同時驗證鄰域分析圖層的不同是否對傳染病時空模擬結(jié)果產(chǎn)生影響.

結(jié)果顯示：① 采用SEIRD-GEOCA時空耦合模型，能很好地模擬COVID-19疫情的時空擴散；② 是否采取封城措施在空間分布上呈現(xiàn)出明顯的爆發(fā)式擴散和局部區(qū)域擴散的差別；③ 實施不同的干預(yù)措施呈現(xiàn)出了不同的時空擴散效應(yīng).封城措施下，有排查能有效避免產(chǎn)生超級傳播者.采取干預(yù)措施，感染者數(shù)量大幅度降低，空間上的擴散被約束在很小的區(qū)域.

傳統(tǒng)的SEIR模型只提供了數(shù)量預(yù)測，并不能給出空間擴散上的指導(dǎo).SEIRD-GEOCA模型在歷史觀測數(shù)據(jù)基礎(chǔ)上，借助SEIRD模型預(yù)測新增確診病例，采用隨機種子點與已有的概率地圖圖層結(jié)合來預(yù)測未來空間的擴散情況，研究范圍內(nèi)精度較高，可以較好地滿足COVID-19疫情的時空預(yù)測.