基于混合模型的優(yōu)化低頻低壓減載方法研究

陳 軍,陸 旭，趙子涵，向 博，朱小紅

(1.國(guó)網(wǎng)四川省電力公司，四川 成都 610041；2.國(guó)網(wǎng)四川省電力公司內(nèi)江供電公司，四川 內(nèi)江 641003)

0 引 言

近年來(lái)，電力系統(tǒng)結(jié)構(gòu)已經(jīng)發(fā)生了巨大的改變，規(guī)模逐漸擴(kuò)大，聯(lián)系程度也日漸緊密[1-3]。電網(wǎng)公司對(duì)常見(jiàn)的單一故障、較嚴(yán)重的故障、罕見(jiàn)的嚴(yán)重故障這三級(jí)標(biāo)準(zhǔn)制定了相應(yīng)的解決措施，稱(chēng)之為保證規(guī)模安全穩(wěn)定運(yùn)行的三道防線(xiàn)[4-5]。目前，電網(wǎng)公司對(duì)第一、第二道防線(xiàn)設(shè)備相關(guān)的在線(xiàn)監(jiān)視、數(shù)據(jù)的信息化管控和數(shù)據(jù)的應(yīng)用與分析已經(jīng)逐漸趨于完善，然而對(duì)第三道防線(xiàn)設(shè)備數(shù)據(jù)的信息化管控能力有限[6-8]。低頻低壓減載屬于第三道防線(xiàn)的范疇內(nèi)。

為了保證電網(wǎng)在受到巨大擾動(dòng)后仍然能保證電力傳輸?shù)姆€(wěn)定性，防止頻率與電壓崩潰事故的出現(xiàn)[9-10]，下面在保證電壓穩(wěn)定的情況下對(duì)低頻低壓減載進(jìn)行了研究，提出了一個(gè)集成遺傳算法與人工神經(jīng)網(wǎng)絡(luò)的混合模型，在低頻低壓情況下進(jìn)行最小化負(fù)荷切除。該方法根據(jù)潮流雅可比矩陣最小特征值靈敏度選擇合適的節(jié)點(diǎn)進(jìn)行負(fù)荷切除。

1 目標(biāo)函數(shù)

建立以最小化減載量以及最大化電壓穩(wěn)定性為目標(biāo)的目標(biāo)函數(shù)[11-12]。所提目標(biāo)函數(shù)F由F1和F2的組合來(lái)表示，分別用于最小化減載量與電壓不穩(wěn)定性，如式(1)—式(4)所示。

目標(biāo)函數(shù)：

F=min{f(F1,F2)}

(1)

(2)

(3)

f(F1,F2)=γF1+(1-γ)F2

(4)

式中：f(F1,F2)為待優(yōu)化的組合目標(biāo)函數(shù)；F1、F2為目標(biāo)函數(shù)；γ為權(quán)重因子；PLi為第i個(gè)節(jié)點(diǎn)的有功功率；Vi為第i個(gè)節(jié)點(diǎn)的電壓值；fi(xmin)和fi(xmax)分別為第i個(gè)節(jié)點(diǎn)的最小限值和最大限值。同時(shí)，為了減少電壓崩潰，使用式(3)，使電壓變化的總幅度最小化。為了在保證電壓穩(wěn)定的情況下實(shí)現(xiàn)最小化減載，因此將權(quán)重因子γ設(shè)定為0.5。

為了優(yōu)化上述目標(biāo)函數(shù)，分別使用了等式和不等式約束，如潮流方程、雅可比矩陣的特征值、發(fā)電機(jī)的有功功率和無(wú)功功率、負(fù)荷節(jié)點(diǎn)的有功功率和無(wú)功功率。這些約束由以下等式詳細(xì)說(shuō)明。

1)功率約束用于計(jì)算當(dāng)前運(yùn)行條件下的功率，以及確定負(fù)載條件和減載后的功率。各節(jié)點(diǎn)處的無(wú)功功率平衡潮流方程如式(5)—式(6)所示。

Pi=Vi∑Vj(Gijcosθij+Bijsinθij)

(5)

Qi=Vi∑Vj(Gijsinθij-Bijcosθij)

(6)

式中：Pi和Qi分別為第i個(gè)節(jié)點(diǎn)的有功功率和無(wú)功功率；i=1,2,…,NB，NB為節(jié)點(diǎn)數(shù)量；j=1,2,…,NPQ，NPQ為PQ節(jié)點(diǎn)的數(shù)量；Gij和Bij分別為節(jié)點(diǎn)導(dǎo)納矩陣第(i,j)個(gè)元素的實(shí)部和虛部。

2)在不等式約束下，考慮了發(fā)電機(jī)和負(fù)荷的有功功率和無(wú)功功率。因此，優(yōu)化問(wèn)題的目標(biāo)函數(shù)可以在更短的收斂時(shí)間內(nèi)達(dá)到。不等式約束條件如式(7)—式(10)所示。

PGn_min≤PGn≤PGn_maxn=1,2,…NG

(7)

ΔPGn_min≤ΔPGn≤ΔPGn_max

(8)

QGn_min≤QGn≤QGn_maxn=1,2,…NG

(9)

ΔQGn_min≤ΔQGn≤ΔQGn_max

(10)

式中：NG為發(fā)電機(jī)數(shù)量；PGn為第n個(gè)發(fā)電機(jī)發(fā)出的有功功率；ΔPGn為第n個(gè)發(fā)電機(jī)的有功功率變化量；QGn為第n個(gè)發(fā)電機(jī)發(fā)出的無(wú)功功率；ΔQGn為第n個(gè)發(fā)電機(jī)的無(wú)功功率變化量。選擇所有節(jié)點(diǎn)電壓的幅值作為當(dāng)前狀態(tài)和減載條件下的不等式約束。

Vi_min≤Vi≤Vi_maxi=1,2,…NB

(11)

3)在潮流雅可比矩陣中，選擇矩陣特征值的最小值作為當(dāng)前運(yùn)行點(diǎn)和減載條件下的不等式約束。

λinitial_min(i)≥λthreshold_min(i)

(12)

λshed_min(i)≥λthreshold_min(i)

(13)

式中：λinitial_min(i)為第i個(gè)節(jié)點(diǎn)在正常工作點(diǎn)的初始最小特征值；λthreshold_min(i)為第i個(gè)節(jié)點(diǎn)的最小特征值閾值；λshed_min(i)為第i個(gè)節(jié)點(diǎn)在減載點(diǎn)的最小特征值。

因?yàn)樽钚p載量取決于系統(tǒng)視在功率特征值的靈敏度，所以根據(jù)潮流雅可比矩陣最小特征值對(duì)減載的靈敏度選擇合適的減載節(jié)點(diǎn)。第i個(gè)節(jié)點(diǎn)最小特征值的變化Δλmin(即特征值靈敏度)由特征值變化的斜率值和負(fù)荷功率的變化計(jì)算得出。

Δλmin=xiΔPi+yiΔQi

(14)

式中：xi為相對(duì)于特征值和有功功率的斜率特性變化；yi為相對(duì)于特征值和無(wú)功功率的斜率特性變化。

(15)

(16)

式中：Δλmin_P與Δλmin_Q分別為有功功率和無(wú)功功率變化量對(duì)應(yīng)的特征值變化量；ΔPi與ΔQi分別為第i個(gè)節(jié)點(diǎn)的有功功率和無(wú)功功率變化量。從式(14)中可以計(jì)算出特征值的變化，特征值的變化表明可以根據(jù)發(fā)電量的變化來(lái)確定最佳減載節(jié)點(diǎn)并給出減載量。

2 混合模型

采用遺傳算法和人工神經(jīng)網(wǎng)絡(luò)相結(jié)合的方法進(jìn)行減載計(jì)算。遺傳算法分為兩個(gè)階段：1)構(gòu)建優(yōu)化模型；2)生成減載模型的數(shù)據(jù)集。遺傳算法的第一階段由式(1)在約束條件下表示。在第二階段，使用遺傳算法生成數(shù)據(jù)集，并用該數(shù)據(jù)集訓(xùn)練神經(jīng)網(wǎng)絡(luò)模型，進(jìn)而提高減載模型的性能。根據(jù)神經(jīng)網(wǎng)絡(luò)模型，對(duì)于給定輸入特征值進(jìn)行減載預(yù)測(cè)。

2.1 遺傳算法

遺傳算法用于最小化負(fù)載有功功率變化和電壓變化[13]。為了最大限度地減少負(fù)荷切除以及電壓變化，遺傳算法被應(yīng)用于兩個(gè)階段。在第一階段，計(jì)算雅可比矩陣的最小特征值，得出進(jìn)行最小負(fù)荷切除的目標(biāo)節(jié)點(diǎn)；然后，通過(guò)使用遺傳算法的第二階段來(lái)減少電壓偏差，從而選擇負(fù)荷切除的數(shù)量；最后，從這兩個(gè)階段遺傳算法的結(jié)果中，產(chǎn)生最佳的訓(xùn)練數(shù)據(jù)集。

遺傳算法由種群初始化、適應(yīng)度評(píng)估、交叉、變異和終止5個(gè)步驟組成[14]。

1)初始化優(yōu)化族群。最小特征向量是按照特征值的范圍隨機(jī)初始化，特征值的范圍從雅可比矩陣的初始特征值中選擇。

λmin=[λmin(1),λmin(2),…,λmin(i)]i=1,2,…n

(17)

式中，λmin(i)為第i個(gè)節(jié)點(diǎn)的最小特征值。

2)計(jì)算初始節(jié)點(diǎn)的適應(yīng)度函數(shù)。在遺傳算法的第一階段，使用式(2)計(jì)算適應(yīng)度函數(shù)；第二階段使用式(3)計(jì)算適應(yīng)度函數(shù)。

λfit_min=[λfit_min(1),λfit_min(2),…，λfit_min(i)]

(18)

Pfit_shed=[Pfit_shed(1),Pfit_shed(2),…，Pfit_shed(i)]

(19)

式中：λfit_min(i)為第i個(gè)節(jié)點(diǎn)最小特征值的適應(yīng)值；Pfit_shed(i)為第i個(gè)節(jié)點(diǎn)負(fù)載功率的適應(yīng)值。

3)在染色體的適應(yīng)值和生成的新染色體之間進(jìn)行交叉操作。在生成新的染色體之后，對(duì)新的染色體應(yīng)用適應(yīng)函數(shù)。

4)在突變中，根據(jù)給定的突變率對(duì)基因進(jìn)行隨機(jī)突變。

5)在終止階段，根據(jù)適應(yīng)度函數(shù)選擇最優(yōu)方案。優(yōu)化過(guò)程的最優(yōu)值表示為λbest_min(i)和Pbest_shed(i)，分別為第i個(gè)節(jié)點(diǎn)的最優(yōu)特征值與第i個(gè)節(jié)點(diǎn)的最優(yōu)減載量。然后，將最優(yōu)擬合值輸入于神經(jīng)網(wǎng)絡(luò)，以訓(xùn)練減載模型。

2.2 人工神經(jīng)網(wǎng)絡(luò)

傳統(tǒng)減載預(yù)測(cè)中，人工神經(jīng)網(wǎng)絡(luò)的訓(xùn)練數(shù)據(jù)集由實(shí)際系統(tǒng)生成，這里采用遺傳算法生成的數(shù)據(jù)作為訓(xùn)練數(shù)據(jù)訓(xùn)練神經(jīng)網(wǎng)絡(luò)。神經(jīng)網(wǎng)絡(luò)的輸入為λbest_min(i)，輸出為Pbest_shed(i)。神經(jīng)網(wǎng)絡(luò)由輸入層、隱含層、輸出層組成[15]。網(wǎng)絡(luò)輸入訓(xùn)練數(shù)據(jù)以及輸出訓(xùn)練數(shù)據(jù)表示為：

λbest_min=[λbest_min(1),λbest_min(2),…，λbest_min(i)]

(20)

Pbest_shed=[Pbest_shed(1),Pbest_shed(2),…，Pbest_shed(i)]

(21)

神經(jīng)網(wǎng)絡(luò)中的反向傳播訓(xùn)練步驟如下：

1)為每一個(gè)神經(jīng)元初始化輸入、輸出以及權(quán)重。

2)確定輸出誤差E。

E=Pbest_shed-PN_shed

(22)

式中：Pbest_shed為目標(biāo)輸出；PN_shed為實(shí)際輸出。

3)網(wǎng)絡(luò)輸出計(jì)算。

(23)

(24)

式中，wi為神經(jīng)元權(quán)重。式(23)—式(24)分別為輸出層與隱含層的激活函數(shù)。

4)根據(jù)式(24)改變神經(jīng)元權(quán)重。

wnew=wold+Δw

(25)

Δw=x·PN_shed·E

(26)

式中，x為學(xué)習(xí)率，變化范圍為0.25～0.5。

5)重復(fù)步驟2至步驟4，直到輸出誤差為最小值。

E<0.1

(27)

當(dāng)訓(xùn)練完成后，神經(jīng)網(wǎng)絡(luò)將可以根據(jù)任意最小特征值確定減載量PN_shed。

3 仿真驗(yàn)證

將提出的混合模型減載方法在MATLAB工作平臺(tái)上實(shí)現(xiàn)。這里采用低頻低壓情況下的14節(jié)點(diǎn)系統(tǒng)對(duì)所提出的混合方法的性能進(jìn)行測(cè)試，評(píng)估負(fù)載最小特征值、節(jié)點(diǎn)電壓和負(fù)載有功功率。

該14節(jié)點(diǎn)系統(tǒng)由1號(hào)和2號(hào)節(jié)點(diǎn)上的兩臺(tái)發(fā)電機(jī)以及3號(hào)、6號(hào)和8號(hào)節(jié)點(diǎn)上的冷凝器組成。節(jié)點(diǎn)電壓的理想范圍為0.95～1.06 pu。此系統(tǒng)中引發(fā)減載的原因是發(fā)電短缺。

首先，根據(jù)雅可比矩陣計(jì)算負(fù)荷節(jié)點(diǎn)的特征值，并根據(jù)計(jì)算出的特征值及實(shí)際功率范圍確定這些節(jié)點(diǎn)的特征值范圍。然后，計(jì)算節(jié)點(diǎn)的靈敏度，并根據(jù)特征值的最大靈敏度選擇減載節(jié)點(diǎn)。

通過(guò)使用柱狀圖分析了混合算法的性能，并與基本情況和遺傳算法的結(jié)果進(jìn)行了比較。圖1—圖3分別展示了節(jié)點(diǎn)的最小特征值、電壓幅值和負(fù)載功率在使用不同方法下的變化情況。

從圖1可以看出，3號(hào)、4號(hào)和14號(hào)節(jié)點(diǎn)的特征值靈敏度最大，根據(jù)這些特征值的靈敏度，可以解決減載問(wèn)題。如圖3所示，在3號(hào)節(jié)點(diǎn)上，遺傳算法計(jì)算的減載量多于混合模型計(jì)算的減載量。比較結(jié)果表明，與基本情況相比，使用混合方法進(jìn)行減載可以達(dá)到最小化減載的效果。所有結(jié)果表明，所提出的混合方法可以實(shí)現(xiàn)最小化減載。

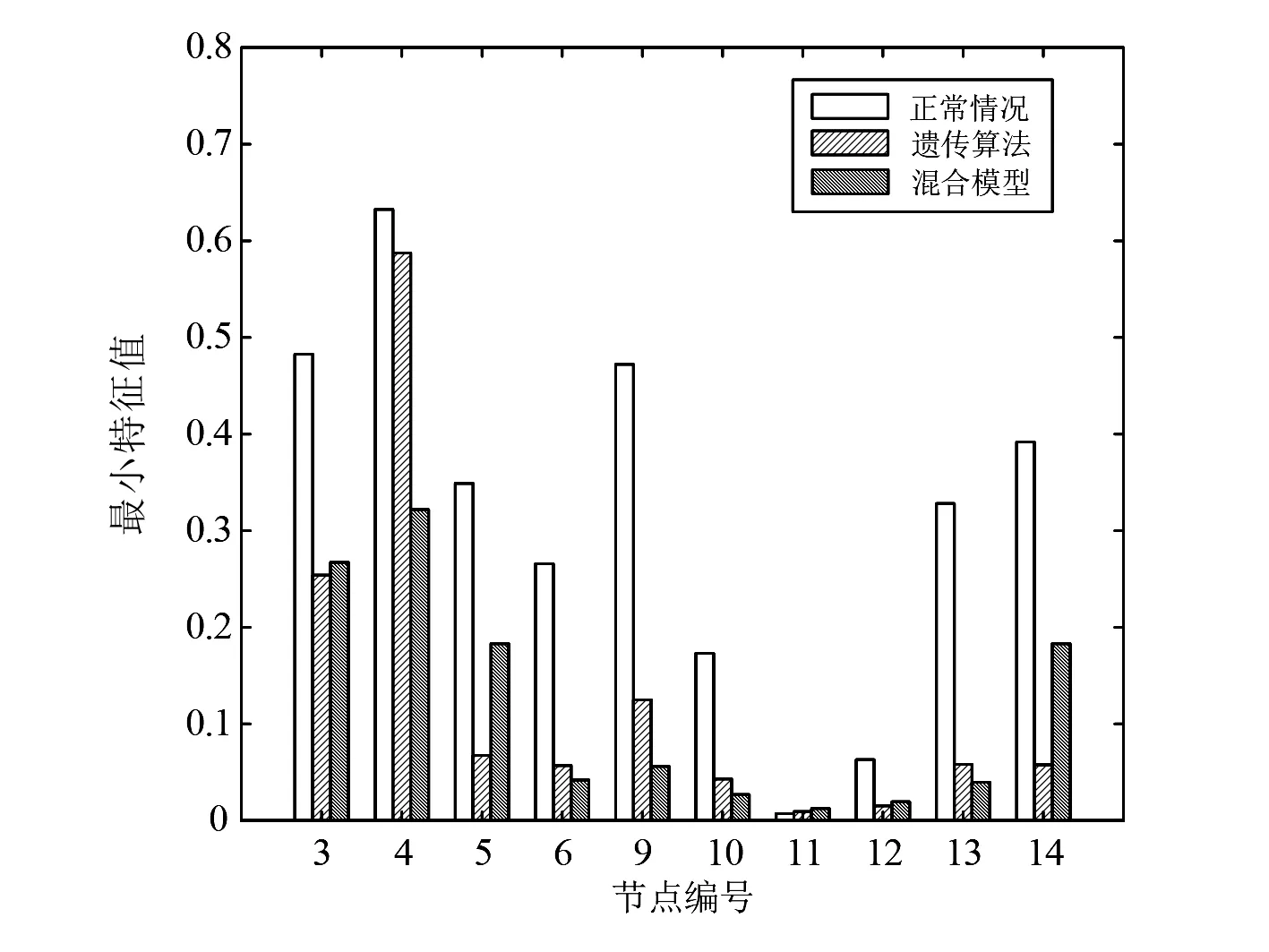
圖1 最小特征值比較

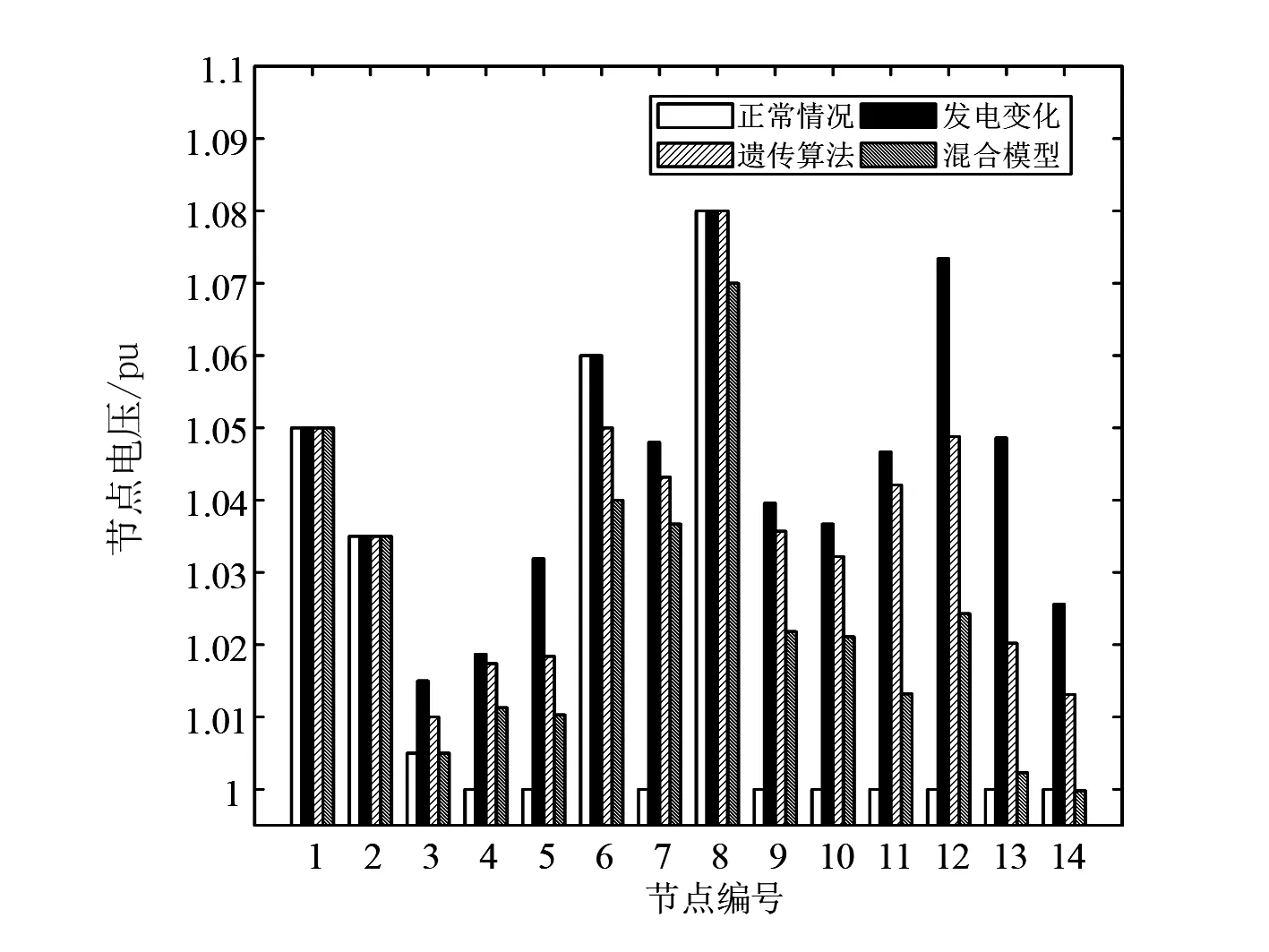
圖2 節(jié)點(diǎn)電壓大小比較

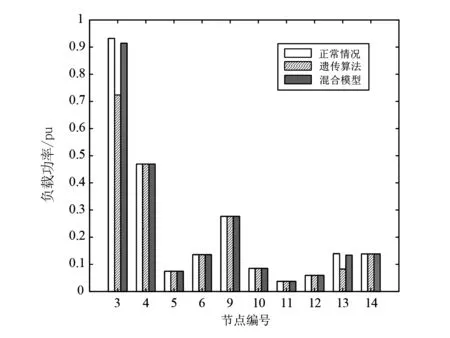
圖3 節(jié)點(diǎn)功率變化比較

4 結(jié) 論

上面提出了一種結(jié)合遺傳算法與人工神經(jīng)網(wǎng)絡(luò)的混合模型，用于在低頻低壓、保證電壓穩(wěn)定的情況下實(shí)現(xiàn)最小化減載的方法。在該混合模型中，遺傳算法分兩個(gè)階段使用，即構(gòu)建優(yōu)化模型和生成用于訓(xùn)練網(wǎng)絡(luò)的數(shù)據(jù)集。根據(jù)潮流雅可比矩陣最小特征值的靈敏度，選擇合適的減載節(jié)點(diǎn)。該算法計(jì)算簡(jiǎn)單，適用于非線(xiàn)性問(wèn)題。將該混合模型在低頻低壓情況下的14節(jié)點(diǎn)系統(tǒng)上進(jìn)行了測(cè)試，并對(duì)其有效性進(jìn)行了驗(yàn)證。結(jié)果表明，該方法可以在低頻低壓情況下實(shí)現(xiàn)最小化減載與最小化電壓波動(dòng)。