多種數值插值算法插值性能分析及優化
張增磊 呂達 趙燈 張強
(1、武漢第二船舶設計研究所,湖北 武漢 430000 2、武漢大學,湖北 武漢 430000)
考慮到強耦合過程的費時、費力、不經濟,目前多體或多場之間的耦合多屬于弱耦合問題。每一次完成弱耦合都需要對耦合面數據進行插值,達到耦合面數據交互的目的[1]。為了尋求更高的插值精度和插值效率,廣大學者提出了大量的插值算法,大致可以分為兩類[2]:函數插值法和投影插值法。函數插值法是直接在高維空間構建插值函數來傳遞耦合數據的一類流固耦合數據傳遞方法,包括最鄰近點插值法[3-4]、加權余量法[5]、基于徑向基函數(RBF)的插值法[6-7]、樣條函數法[8]等。投影插值法是先將待插值的網格節點以某種方法投影后再構建插值函數傳遞耦合數據的一類流固耦合數據傳遞方法,包括映射點插值法[9]、常體積轉換方法[10]、載荷面法[11]、定義局部坐標[12]和引入數據降維方法等距映射法ISOMAP[13]。
為了實現耦合面之間壓力的準確傳遞,本文針對最臨界點插值法、最小二乘插值法和等距映射法,利用數據計算,分析了網格數目、網格質量和耦合面邊界類型對插值精度和插值效率的影響規律,并提出了一種基于網格循環的插值策略,當耦合面采用高階單元時,可以提高耦合面插值效率,對耦合面總壓力的傳遞具有較高的準確率。
1 三種常見的數據插值算法
1.1 最鄰近點插值法(NN)
最鄰近點插值法(NN)實現方式較為簡單,通過對耦合面網格所有節點進行遍歷,將距離最近的節點載荷數據作為待插值節點的載荷數據。
為獲取待插值點M(x, y, z)的載荷數據,通過式(1)獲取該節點與源耦合面節點M′(xi, yi, zi)的距離

m 為源耦合面最大節點編號。若節點i 的載荷數據為N(xi,yi, zi),則節點M的載荷數據為N(xi, yi, zi)。
1.2 最小二乘多項式插值法(L2)
通過選取與待插值點M(x, y, z)臨近的k 個節點的載荷數據,構建如式(3)所示的多項式進行數據插值,獲取待插值點的載荷數據。
首先,依據源耦合面內k 個臨近節點構建載荷矩陣方程P=AB,其中
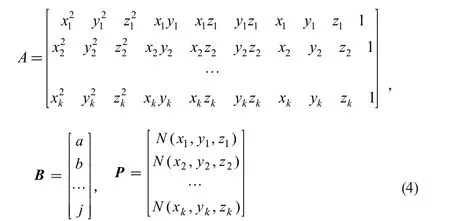

1.3 等距映射法(ISOMAP)
等距映射法是基于多維尺度分析(MDS)的非線性降維算法,可以消除耦合面空間非線性對耦合數據傳遞的影響。該算法先采用鄰域歐式最短距離估計點與點之間的距離,然后應用多為尺度分析計算在和數據的低維插值載荷數據。該過程的實現可分為以下三個步驟。
(1)構造鄰域圖。若源耦合面內節點總數為N,采用K- 鄰域判斷源耦合面內任意兩節點(i, j)是否相鄰,若相鄰,則確定節點距離d(i, j),并最終構建鄰域圖G。
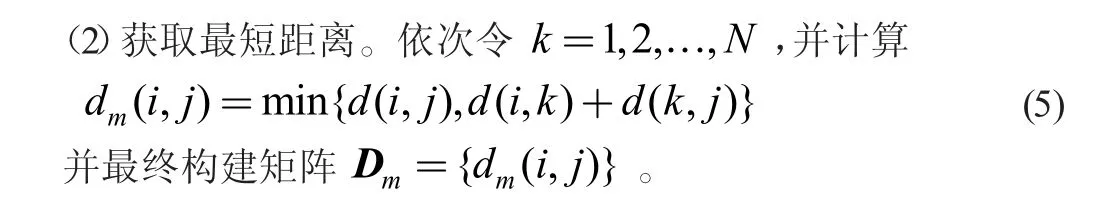
(3)構建d 維插值。對矩陣Dm應用MDS 算法構建最小化目標函數
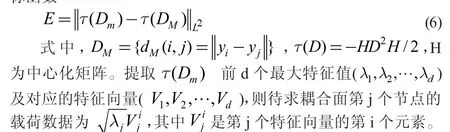
2 三種插值算法的插值性能分析
如圖1 所示,本文擬定兩個物理場的耦合面尺寸均為100mm×100mm,源耦合面網格節點均勻分布,而待求耦合面的網格節點依據給定的平均單元尺寸均勻分布或自由生成。通過對比最鄰近點插值法、最小二乘多項式插值法和等距映射法三種插值算法的插值計算時間、插值誤差進行對比,分析了不同耦合面網格尺寸、網格質量和耦合邊界類型對三種插值算法的插值效率和插值精度的影響。
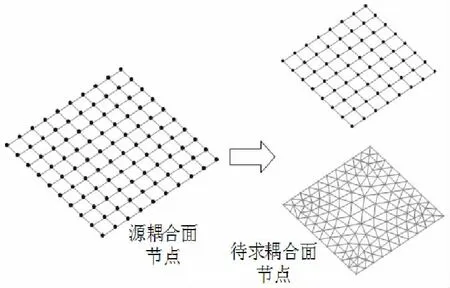
圖1 耦合面節點分布示意圖
2.1 網格尺寸
在分析單元尺寸對插值計算的影響時,本文設置待求耦合面采用網格自由劃分方式,更改耦合面單元尺寸,耦合面節點數據如表1 所示。
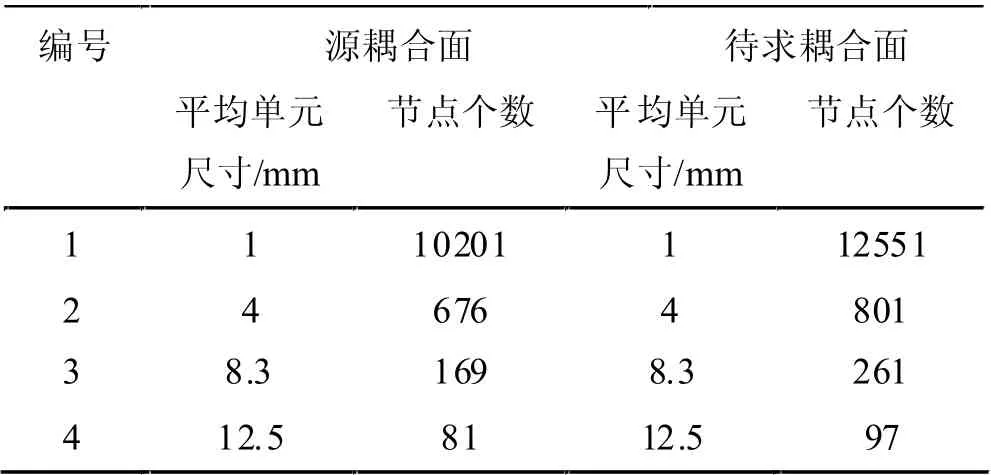
表1 耦合面網格尺寸設置

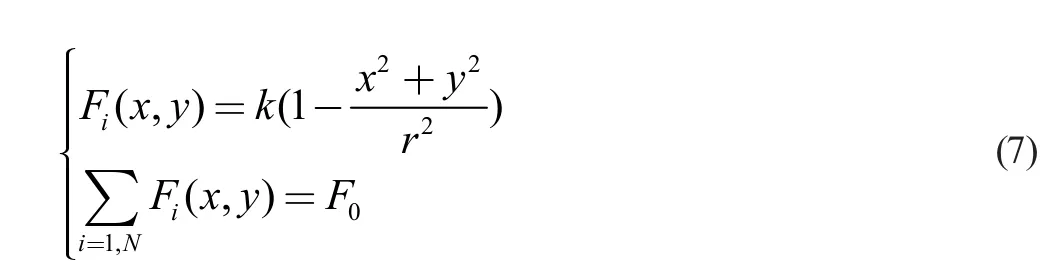
最鄰近點插值法、最小二乘多項式插值法和等距映射法三種插值算法的傳遞的總壓力和插值時間如圖2 所示。
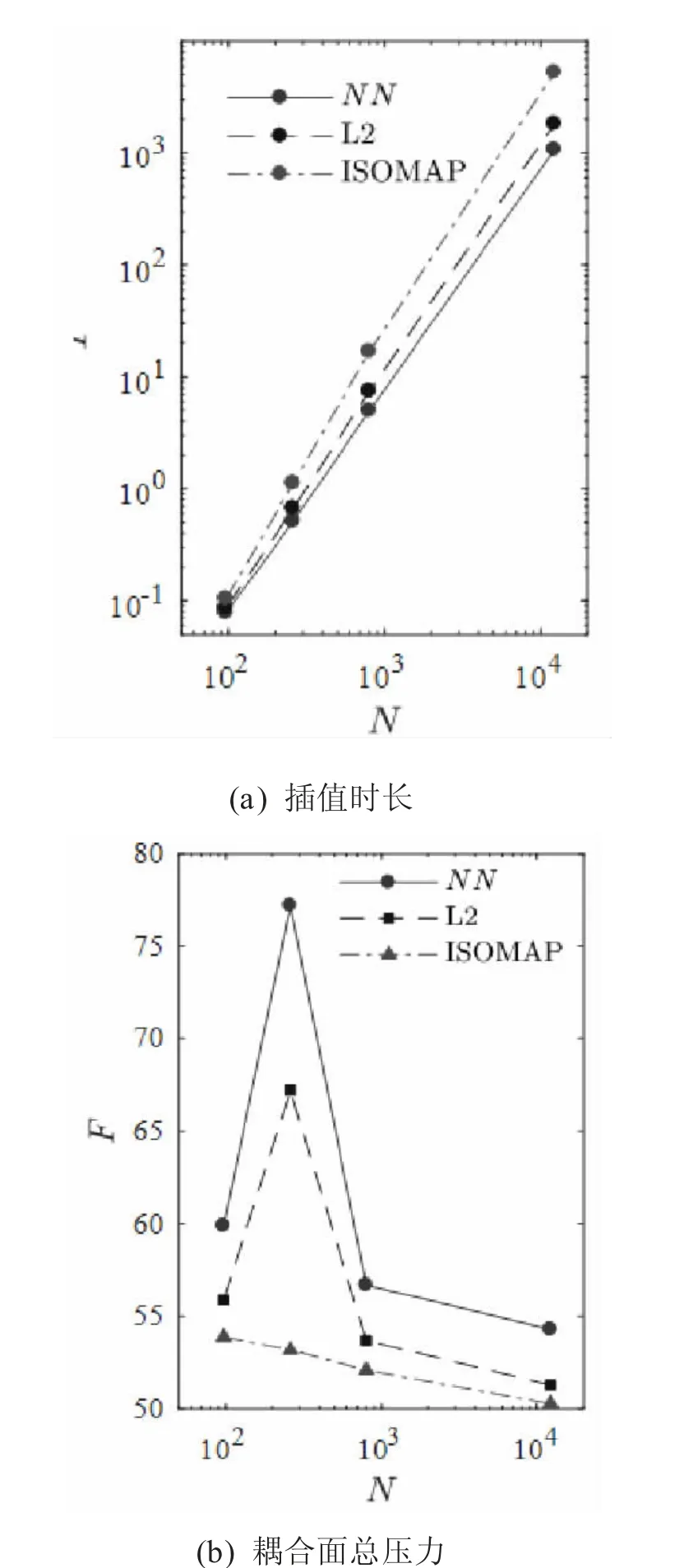
圖2 網格尺寸對插值效率和插值精度的影響
當兩個耦合面單元尺寸相近時,改變網格尺寸,插值時長與耦合面節點在對數坐標系下呈現正相關,即T∝Nk。對于三種插值算法,指數k 分別為1.97,2.05,2.14。最鄰近點插值法在整個插值過程中,包含兩類循環:一種是對待求耦合面所有節點進行循環,獲取每個節點的壓力值;另一種是對源耦合面所有節點進行循環,獲取源耦合面內待求節點的最鄰近節點。而第二種循環中嵌套在第一種循環中,導致了該算法的系數k 接近2。而最小二乘多項式插值法和等距映射法并不僅僅依靠最鄰近節點的壓力值而確定,會根據臨近多個節點進行擬合,獲取待插值點附近的更加準確的壓力分布,導致插值效率均低于最鄰近點插值法。
最鄰近點插值法在求解每個節點壓力時由較大誤差,導致了計算所得的總壓力大于源耦合面的總壓力,通過折算降低節點數目不等帶來的誤差后,最大誤差仍可達到34.9%。由于該插值算法中耦合面各節點互不干擾,獨立計算,當節點個數多于源耦合面節點數時,多出的節點必然會增加耦合面的總壓力。最小二乘多項式插值法也存在類似的不足之處。當節點數較少時,源耦合面節點承受的壓力遠高于節點數多的情形,多出的節點數目對總壓力的計算影響較大,導致了傳遞的總壓力隨著節點數的增加而呈現先增大或降低的趨勢。而等距映射法會構建鄰域圖,節點之間會相互影響,減弱多出的節點對計算的影響,插值精度也會隨著節點數目的增加而緩慢增加,但仍會增大傳遞的總壓強。
若以式(7)獲取的待插值點處壓力為準確數據,則第三組所有插值點的相對誤差如圖3 所示。
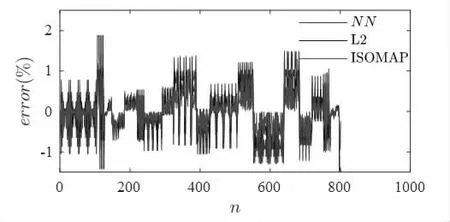
圖3 待插值節點壓力誤差
由圖3 可知,三種插值算法均能保證每個節點的相對誤差小于2%,但最鄰近點插值法的插值精度明顯弱于最小二乘插值法和等距映射法。對于同一套網格,利用三種算法計算的節點壓力的相對誤差的分布基本一致。由此圖可以推斷,網格質量或者節點分布均勻性對插值精度具有顯著的影響。若降低耦合面節點數目,必然導致源耦合面節點之間梯度變大,會加劇插值點的相對誤差,特別是對最臨近點插值法。
2.2 網格質量
為了研究耦合面節點的分布對插值過程的影響規律,在耦合面節點數目相同的基礎上,選定了三種待求耦合面節點分布,網格質量從左往右依次增加,示意圖如圖4 所示。在源耦合面上施加式(7)所示的壓力,三種插值算法的插值時長和耦合面總壓力如圖5 所示。提下,等距映射法插值效率最低,最鄰近點插值法插值效率最高,高于等距映射法的兩倍。
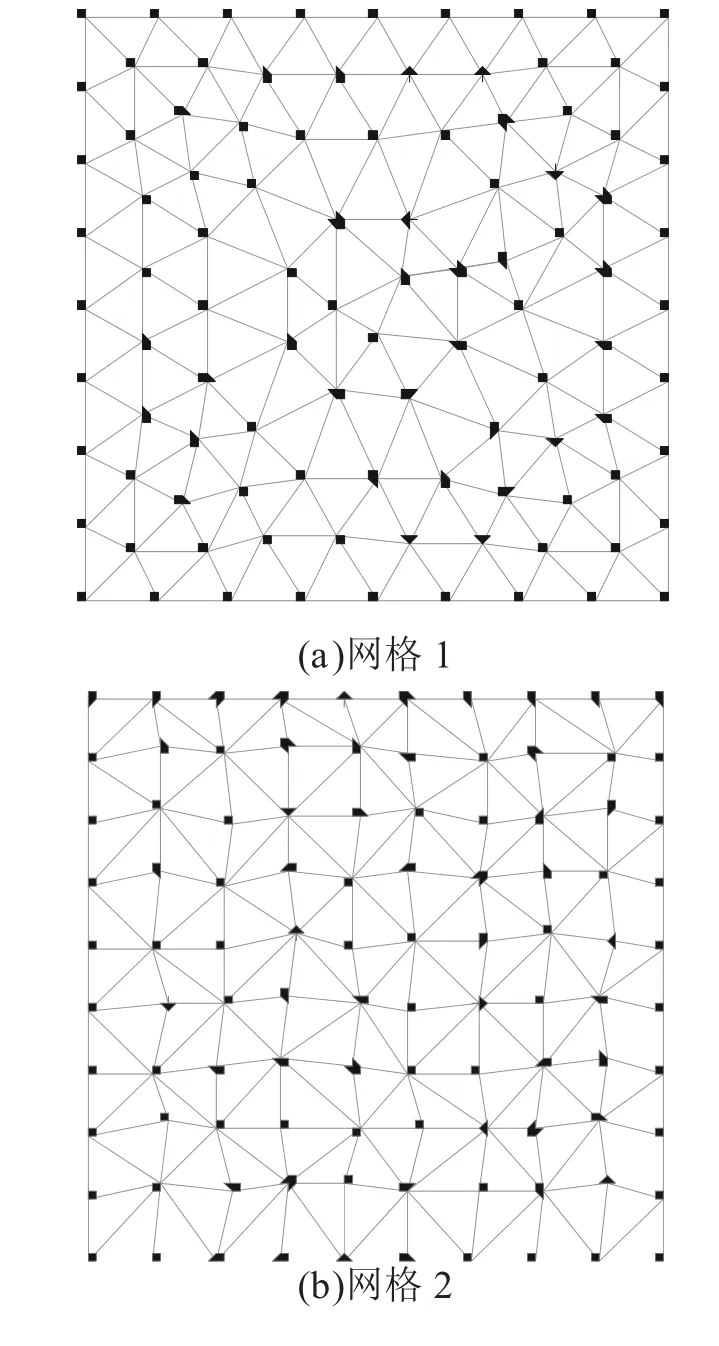
圖4 不同網格質量的待求耦合面節點分布
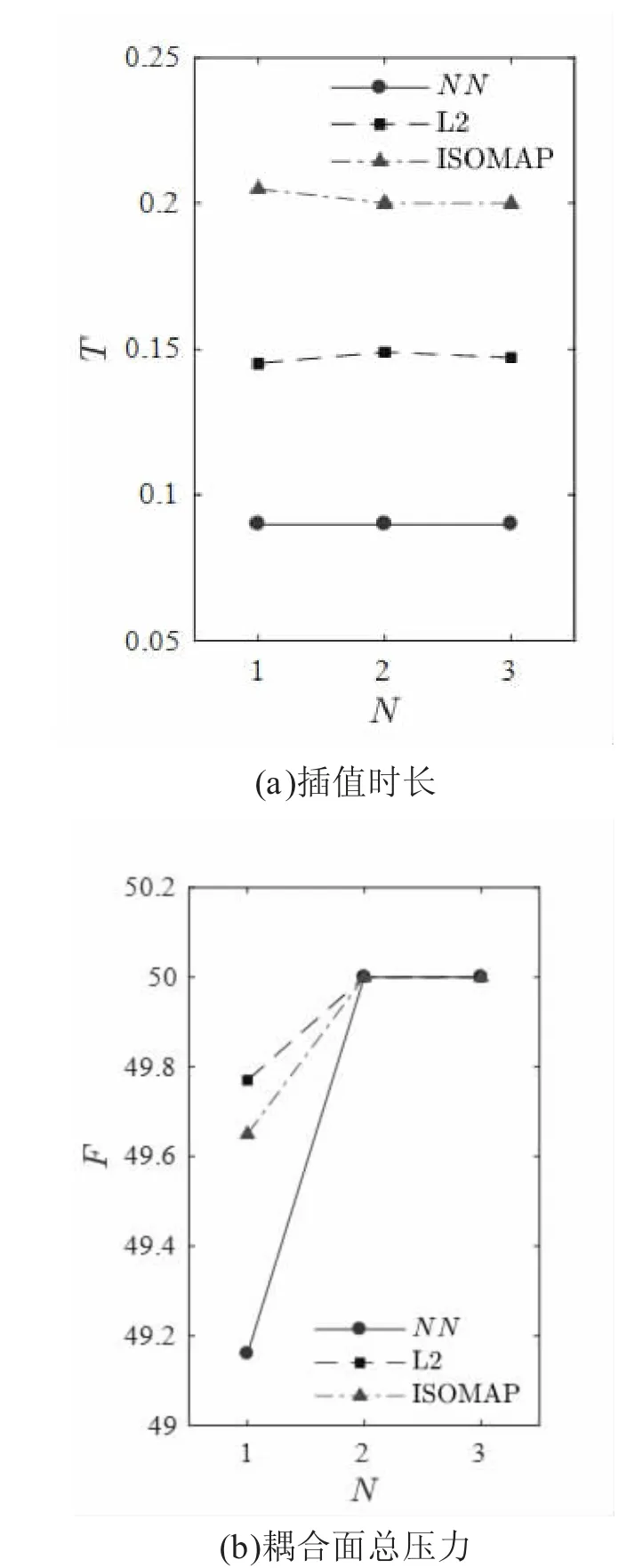
圖5 網格質量對插值效率和插值精度的影響

由圖5(b)可知,質量較高的網格可以提高插值精度。在提供的三種網格中,三種插值算法僅對網格1 產生較大的插值誤差,大小分別為1.68%,0.46%和0.70%,而對網格2 和網格3 的插值誤差均低于0.01%。
在不同網格質量下,每個節點壓力的相對誤差如圖6 所示,其中網格3 導致了相對誤差均為0,則并未附圖進行說明。從左往右分別利用了最臨近點插值法、最小二乘插值法和等距映射法進行計算。

圖6 節點插值壓力的相對誤差
圖6 直觀地展現了網格質量對插值精度的影響。當網格自由劃分時,節點一般會在靠近邊界的區域無規律分布,而恰好在該區域,節點的相對誤差較大,且變化明顯。針對網格2 和網格3,當節點分布較為均勻時,節點的相對誤差普遍較小,插值更加準確。
3 結論
本文介紹了三種常見的數據插值算法,分析了網格尺寸、網格質量對插值性能的影響規律,并提出了一種利用網格遍歷的插值優化策略,得到如下結論:

3.2 網格尺寸、網格數目對插值精度影響較大,三種插值算法對三種參數的敏感程度也不一致,且三種參數對三種插值算法在插值精度上的影響程度分別是最鄰近點插值法、最小二乘插值法和等距映射法。若以壓力作為傳遞參數,耦合面節點數目對傳遞的總載荷影響較大,待求耦合面節點數大于源耦合面節點數,導致了傳遞的總載荷增大,增大幅值近似于兩耦合面節點數之比。質量高或節點分布均勻的網格,耦合面變化梯度較小均有利于降低整體節點的壓力相對誤差,提高插值精度。若網格節點數目較少,甚至網格質量不高時,最臨界點插值法的插值精度會急劇增高,在本文所計算的數據中,最高可達到34.9%。

