機器人加工裝備運動學鏡像模型建立方法與實驗研究

南曉萱 王 俊 肖 明 席文明

(廈門大學航空航天學院，福建 廈門 361102)

在自動化制造階段，操作者通過示教器操縱機器人，形成操作者與機器人的直接關聯，這種模式適合大批量、產品單一的制造過程。在數字化制造階段，為適應多品種、少數量的訂單式生產，構建了與物理系統對應的數字系統，即物理系統的鏡像模型,實現數字系統對物理系統功能的部分替代，適應快速變化的制造過程[1-2]。在智能制造階段，為替代物理系統的更多功能，在鏡像模型的基礎上，實現數據的雙向傳輸，從而建立物理系統與數字系統的數字孿生[3-5]，通過物理系統的傳感數據，實現對物理系統的模擬、仿真與參數優化[6]。

建立物理系統的鏡像模型是實現智能制造的基礎，然而，由于機器人制造、安裝誤差的存在以及機器人串聯式結構，其物理機器人幾何參數與數字空間中的理論參數并不一致，導致機器人絕對定位精度低。構建物理機器人鏡像模型的方法是對機器人的本體和裝備進行標定[7]，利用標定的參數，實現數字空間中物理機器人的鏡像模型構建。標定精度決定著建立的鏡像模型精度，從而決定著機器人的作業精度。

現有標定方法沒有考慮零位誤差，即機器人零位時實際關節角與理論關節角差值對幾何參數標定的影響，導致標定后幾何參數的較大誤差[8]，降低了鏡像模型精度和機器人的作業精度。本文采用軸旋轉法標定方法，實現幾何參數與零位的解耦標定。利用坐標變換法建立標定后機器人的運動學方程，借助牛頓迭代法求取運動學逆解。

1 軸旋轉法標定機器人關節軸線

圖1是標定機器人幾何參數的實驗系統，由安川MH250機器人(日本安川公司，抓取重量250 kg，工作空間2 700 mm)、Radian激光跟蹤儀(美國自動精密工程公司，測量精度為5 μm)以及安裝在機器人末端電主軸連接塊上的靶球組成。標定過程為：①驅動機器人至零位。②在盡可能大的角度范圍內，按一定的角度間隔只旋轉一個軸而其他軸固定，記錄對應角度間隔的靶球空間坐標。③將靶球安裝到電主軸連接塊的另一個位置，重復②，即同一個軸測量兩次。④標定完一個軸后，重復①～③過程，直到所有關節軸標定完成。

對于記錄的同一個軸的兩組數據，它們處于繞該軸旋轉形成的空間圓上，如果能夠利用2組數據求得空間圓的圓心，則2個圓心的連線就是該軸的軸線。計算方法如下：

設測量點的坐標為Ki(xi，yi，zi)，i=1，2，...，n。空間平面的方程為：

apx+bpy+cpz-1=0

(1)

將n個測量點代入式(1)中，得：

ApXp-Lp=0

(2)

(3)

空間球方程為：

x2+y2+z2-Ax-By-Cz+D=0

(4)

將n個測量點代入公式(4)并以矩陣形式表示：

QqXq-Lq=0

(5)

則其最小二乘解為：

(6)

apx0+bpy0+cpz0-1=0

(7)

又向量O0平行于擬合平面的法向量(ap，bp，cp)，則：

(8)

聯立式(7)、(8)，可得擬合平面與擬合球相交的截圓圓心坐標：

(9)

設第二次擬合圓的圓心為o′(x01,y01,z01)，連接兩圓圓心，得到軸線的向量為：

n=(x01-x0,y01-y0,z01-z0)

(10)

軸線向量n已知，又軸線過擬合圓圓心o(x0,y0,z0)，則軸線方程為：

(11)

2 機器人運動學方程建立

由于制造和安裝誤差，導致物理機器人的軸線由理論的平行或垂直狀態變為不平行、不垂直，并且末端三軸不交于一點，無法采用D-H法建立運動學方程。圖2中，{in}表示理論模型的第i軸連桿坐標系，{ia}表示物理機器人第i軸連桿坐標系，li表示機器人基坐標系中第i軸的方向向量。

{in}繞ki軸旋轉λi角使旋轉后坐標系各坐標軸平行于{ia}坐標系各坐標軸，得到新坐標系{i1n}；然后將新坐標系{i1n}沿向量npi進行平移與坐標系{ia}重合，其中：

(12)

由各軸軸線的空間位姿，可以得到物理機器人的零位，見表1所示。

表1 機器人理論零位和實際零位值 (°)

假設理論模型各連桿坐標系相對于機器人基坐標系的位姿矩陣為Ii，則物理機器人各連桿坐標系相對于基坐標系的位姿矩陣Qi可通過式(13)進行求解：

Qi=IiTrans(npix,npiy,npiz)Rot(ki,λi)

(13)

式中：npix、npiy、npix是向量npi在坐標系{in}的3個坐標軸上的投影。

(3)繞{(i-1)2a}的z軸旋轉θi，使得{(i-1)2a}的姿態與{ia}完全一致，得{(i-1)3a}。

(4)沿向量Si(Six,Siy,Siz)平移，使得{(i-1)3a}最終與{ia}完全重合。

可得：

(14)

αi=arccos[(a(i-1)xaix+a(i-1)yaiy+a(i-1)zaiz)cosβi-1+

(n(i-1)xaix+n(i-1)yaiy+n(i-1)zaiz)sinβi-1]

(15)

(16)

求得的Qi數值代入式(14)～(16)，即可求得物理機器人的連桿參數，見表2所示。

表2 物理機器人連桿參數

物理機器人相鄰變換矩陣為：

(17)

其中：s表示sin，c表示cos。

根據正運動學方程的定義，得：

LS=MA

(18)

其中：L為投影矩陣，MA為給定機器人的末端位姿。矩陣取等式兩邊矩陣的前3行元素對應相等，構造方程組如下：

(19)

其中：f1(θ)～f12(θ)均是關于變量θ(θ1θ2θ3θ4θ5θ6)的多元函數，記為F=[f1(θ),f2(θ),…，f11(θ),f12(θ)]T。物理機器人逆運動學求解的本質是求方程組F關于變量θ的解，使用牛頓迭代法求解該方程組，具體步驟如下：

(1)首先求解方程組F的雅可比矩陣J(θ)，并構造θ求解的迭代公式。方程f1(θ)～f12(θ)分別對變量θ(θ1θ2θ3θ4θ5θ6)求偏導數，得到方程組F的雅可比矩陣J(θ)，如式(21)所示。

(20)

計算雅可比矩陣J(θ)的廣義逆矩陣，并由此得到θ求解的迭代公式，如式(21)所示。

θk+1=θk-[JT(θk)J(θk)]-1JT(θk)F(θk)

(21)

(2)利用機器人理論模型的逆運動學解，作為牛頓迭代的初值θ0。

(3)根據迭代公式(21)更新變量θ的值。

(4)根據加工要求給定迭代精度ξ，本文取小數點后4位。計算關節變化量dθ=θk+1-θk，判斷‖dθ‖∞≤ξ是否成立，若成立，取θ當前值作為物理機器人的逆解；若不成立，重復步驟③～步驟④，直至‖dθ‖∞≤ξ成立或超出迭代次數。

3 機器人加工裝備鏡像模型建立

物理機器人運動學標定完成后，就可以利用標定的參數建立物理機器人的鏡像模型。圖5a是物理機器人系統，圖5b是利用ADAMS軟件建立的與圖5a對應的鏡像模型，其方法是按照標定的參數建立各桿件CAD模型并將其導入到軟件中，按照標定的幾何參數裝配成鏡像模型。

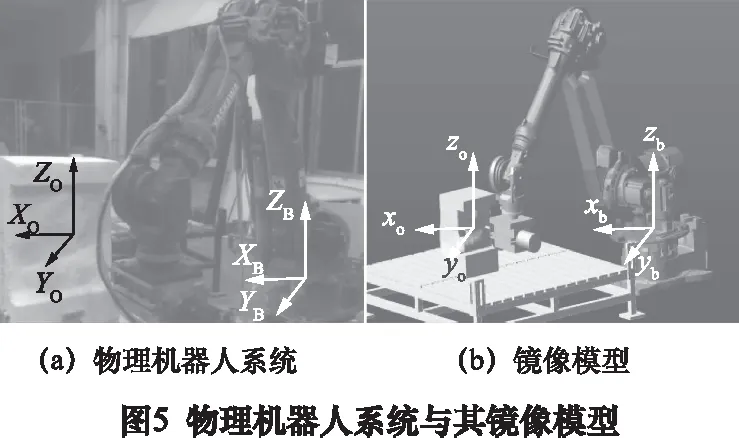
建立物理機器人的鏡像模型后，還需要建立機器人加工裝備的鏡像模型，即圖5a中的其他單元相對于機器人的位姿，與圖5b中的對應單元模型相對于機器人模型的位姿一致。以加工對象為例，設圖5a中加工對象的坐標系為{XOYOZO}，機器人坐標系為{XBYBZB}，它們之間的轉換矩陣為J1。圖5b中加工對象模型的坐標系為{xoyozo}，機器人模型坐標系為{xbybzb}，它們之間的轉換矩陣為J2。建立機器人加工裝備鏡像模型的方法為：在物理空間，利用標定后的機器人作為測量工具測量J1的值，然后在鏡像模型空間中，利用測量的J1值調整加工對象模型的位姿，即調整{xoyozo}的位姿，使得J2=J1。機器人加工裝備中其他單元的鏡像模型建立與此相同。

完成物理機器人本體和裝備的鏡像模型建立后，可以在數字空間中集成刀軌跡生成與后處理模塊以及加工仿真模塊，實現物理機器人加工前的軌跡生成與優化、加工仿真等。

在圖5b中，針對加工對象模型，CAM軟件生成的刀軌跡是相對于{xoyozo}坐標系，需要將刀軌跡通過{xoyozo}坐標系，轉換到機器人坐標系{xbybzb}中，生成機器人軌跡，這一過程被稱為刀軌跡后處理。{xoyozo}與{xbybzb}之間的轉換矩陣為J2，通過J2易于將刀軌跡轉換成機器人軌跡。

4 實驗驗證

圖6是沿長方體四周加工凹槽，通過測量凹槽加工后的錯位誤差以及尺寸精度，驗證物理機器人與裝備鏡像模型建立的有效性。采用理論運動學模型控制機器人加工的最大誤差為4.02 mm，而采用標定幾何參數的運動學模型控制機器人加工的最大誤差減少到0.28 mm。通過機器人幾何參數的標定，可以有效提高鏡像模型的精度，從而提高機器人的加工精度。

圖7a是采用變姿態對半球體進行加工，加工時，其刀具軸線指向球心，圖7b是完成加工后的半球，圖7c是半球加工后的誤差測量方法，即沿不同的d處，測量球冠半徑R。其中球體半徑為50 mm，d值以5 mm為間隔，共測量8次，每次重復測量10次，取其平均值。半球體加工的誤差范圍為-0.83～+0.52 mm，這其中部分誤差來源于電主軸連接塊的安裝和制造誤差，導致鏡像模型空間與物理空間的工具中心點(TCP)坐標系不一致而形成的誤差。

5 結語

本文利用軸旋轉法標定方法求取物理機器人的幾何參數，利用求取的幾何參數構建物理機器人的鏡像模型，為物理機器人數字孿生體的構建建立了基礎。后期，將利用機器人廠家提供的開發庫，獲取物理機器人的狀態參數以及加工參數，實現物理系統與數字系統間的數據雙向傳輸，建立物理機器人系統的數字孿生體，實現加工過程的監督與加工參數的優化。