非規則坡面形態對高位滑體失穩的影響研究

胡昌文，趙騰，龔小根

（1.深圳市綜合交通設計研究院有限公司，廣東 深圳 518003；2.中南大學 土木工程學院，湖南 長沙 410075）

滑坡與靜態邊坡的穩定性分析不同，是一個變形、解體、運動、堆積的動態過程[1-5]。在中國，滑坡地質災害日漸增多，造成了嚴重的人員傷亡和慘重的經濟損失。因此，研究滑體失穩，提高邊坡穩定性，至關重要[6]。針對滑坡失穩過程中的運動特性，國內外進行了很多研究。崔濤[7]針對壺大某公路段改擴建工程邊坡滑坡災害，通過現場工程地質調查與勘探，分析邊坡滑坡失穩機制，提出了加固方案，并采用數值分析方法進行驗證。魯志雄等人[8]運用地貌學和工程地質力學等方法對滑坡變形失穩影響因素進行分析，并提出應合理規劃以減少災害的發生。王升等人[9]采用更新拉格朗日控制方程的物質點法，建立了滑坡二維模型，模擬滑坡失穩、運動和沖擊過程，其結果表明：物質點法模擬分析獲得的滑坡滑裂面形態、失穩和運動特征與實際觀察結果較吻合。潘萬成等人[10]對滑坡地質條件、變形發育特征進行分析，并結合FLAC3D 數值模擬論證了滑坡的不穩定性，提出“地表排水＋抗滑樁＋格構錨桿”的綜合治理對策。Li 等人[11]采用簡化Bishop 法，分析了軟弱層傾角變化下邊坡穩定性變化規律，明確了軟弱層對邊坡滑移模式及穩定性的影響。ávila 等人[12]以65 個滑坡為研究對象，利用物理模型FS FⅠORⅠ對可能影響邊坡失穩因素進行了反演分析。Subramanian 等人[13]提出了一個空間分布和順序耦合數值模型，模擬了融雪水誘發流域尺度的邊坡失穩。該模型不僅能夠較好地預測融雪水誘發滑坡的觸發條件、震級和空間分布，而且具有較好的精度。影響滑體失穩運動的因素較多，但以坡表幾何形貌作為影響因素，研究對滑體失穩特征影響的較少。因此，作者擬針對該影響因素，基于離散傅里葉逆變換的邊坡坡表輪廓重構法，以顆粒單元組成失穩滑體，將未失穩坡體設置成為靜止不動的墻體，準確生成非規則坡面的幾何邊坡模型，并導入PFC 2D 軟件進行數值計算，通過設置監測顆粒和滑體分組，有效模擬了滑體顆粒在不同坡面輪廓下的運動軌跡，可為研究非規則坡面滑坡提供借鑒。

1 PFC 2D 工作原理及離散傅里葉逆變換

1.1 PFC 2D工作原理

與建立連續介質模型的有限元軟件不同，PFC 2D 離散元軟件以分子動力學為基本原理，建立非連續介質模型，軟件的基本單元為相互獨立的離散顆粒單元與墻體單元。本研究采用平行黏結模型，它包含5 個微觀力學參數：切向黏結強度、法向黏結強度、切向剛度、法向剛度、黏結半徑。每一個顆粒單元都能夠在外力作用下獨立運動，運動方式為轉動或平移，顆粒間既能傳遞力，也能傳遞彎矩。基于FⅠSH 語言編寫程序，分別給顆粒和墻體賦予不同材料參數，并在每個時步內更新單個顆粒、顆粒與顆粒、顆粒與墻體之間的速度、加速度、接觸力等信息。當系統平均不平衡力與平均接觸力之比小于1×10-5時，認為模型處于平衡狀態。

PFC 2D 中，顆粒單元與墻體單元的循環計算如圖1 所示。從圖1 中可以看出，顆粒單元與墻體單元信息的更新計算是一個反復循環的動態過程，在每一個循環過程中，通過運用牛頓第二定律（運動方程），計算得到每個顆粒單元的合力及合力矩。同時，對每個接觸使用力-位移方程進行求解，更新顆粒單元與墻體單元的位置信息，生成新的接觸，如此不斷循環計算并更新信息，直至模型達到平衡，計算停止。

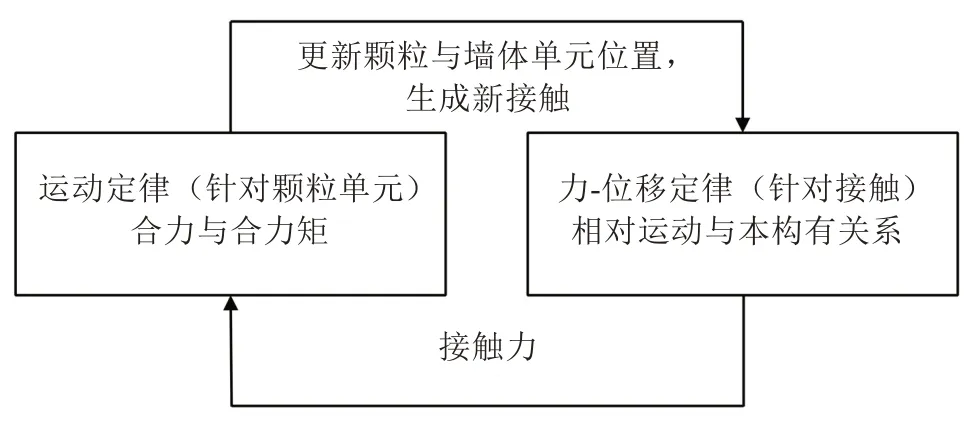
圖1 計算循環示意Fig.1 Schematic diagram of calculation cycle

1.2 邊坡坡表幾何特征分析

以某路基邊坡工程為例，對該坡表幾何特征進行分析。該路基右側邊坡的邊坡剖面線示意圖如圖2 所示。在圖2 中，共5 條剖面線，利用GⅠS軟件可分別得到相應的邊坡剖面基線，本研究選取b、d 2條邊坡剖面線進行分析。

圖2 路基右側邊坡剖面線示意（單位：m）Fig.2 Schematic of the section line of the right side slope of the roadbed（unit:m）

剖面b、d 的邊坡剖面基線圖與剖面線起伏分量圖如圖3 所示。從圖3 中可以看出，邊坡剖面線上局部起伏特征明顯，其中，圖3中的剖面基線圖中的直線是運用線性最小二乘法得到的整體坡度線，由此可以得到邊坡坡面局部的起伏分量。邊坡表面的非規則形態蘊含在該起伏分量中，即形態數據在一定水平（基線）上表現出有規律的波動。邊坡剖面的起伏分量呈現多個頻率的三角函數疊加特征，其中，低頻成分較多，高頻成分較少，而離散傅里葉正反變換分析法可以有效地描述這種規律性。因此，可基于離散傅里葉逆變換對非規則邊坡輪廓進行重構。

圖3 剖面b、d的邊坡剖面基線與剖面線起伏分量圖Fig.3 The slope profile baseline and profile line fluctuation component diagram of the section b and the section d

1.3 基于離散傅里葉逆變換的邊坡坡表輪廓重構

在信號處理時，離散傅里葉逆變換（inverse discrete fourier transform，簡稱為ⅠDFT）具有將離散的頻域信號合成為離散時域信號的特點。因此，坡表輪廓的生成過程中，可應用離散傅里葉逆變換的方法，將坡表輪廓視為時域信號，并將其基本公式[14]通過適當改寫，可得到[15]：

式中：n為諧波編號為諧波總個數；y為最終i通過離散傅里葉方法合成坡表輪廓在y方向的坐標值；y0為離散信號的均值；θi為坡表輪廓表達式的自變量；An和Bn為離散傅里葉正變換后得到的2個頻域信號；?n為初相位；

由式（1）～（5）可知，當待分析的坡表輪廓線的離散點總數一定時，坡表輪廓線可完全分解為傅里葉描述因子Dn和初相位?n，n=1,2,3,…,64，二者均為無量綱數，即Dn和?n包含坡表輪廓線的全部幾何特征。Dn本質上是三角函數的幅值，直接決定諧波的起伏程度（坡表輪廓線的主要形態），而初相位?n決定了各諧波在傳播方向的平移情況。

1.4 傅里葉描述因子

根據文獻[15]可知：傅里葉描述因子Di代表三角函數的幅值，其頻譜整體為遞減趨勢，頻譜分布情況大致為對數形式，可采用式（6）進行擬合。

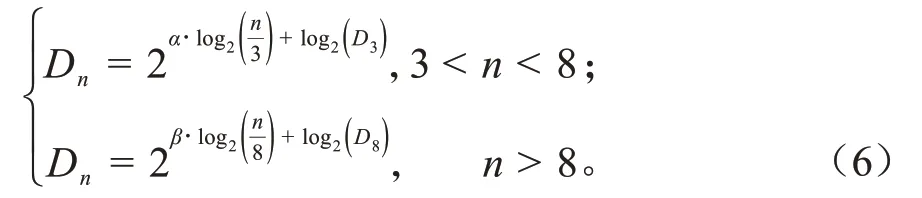
其中，α=－1.40，β=－1.35，二者皆為無量綱的修正系數，D2、D3、D8為擬合公式中的自變量。

根據傅里葉描述因子對坡表幾何形貌的控制作用，可以將傅里葉描述因子分為D2，D3→D7和D8→D64三大類。這三大類控制作用相應地由D2、D3、D8所決定，其中，D2控制坡面曲線較大的均勻起伏程度，D3控制坡面曲線較小的非均勻起伏程度，D8控制坡面曲線的最小起伏（即粗糙程度），如圖4～5所示。

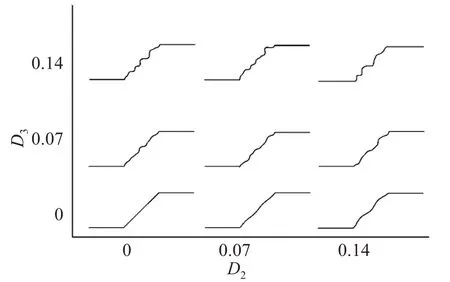
圖4 D2與D3對坡面幾何形貌的影響（D8=0）Fig.4 Ⅰnfluence of the D2 and D3 on slope geometry（D8=0）

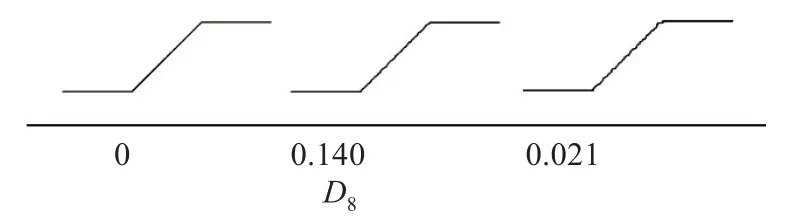
圖5 D8對坡面幾何形貌的影響（D2=D3=0）Fig.5 Ⅰnfluence the D8 on slope geometry（D2=D3=0）

2 坡表幾何形貌對高位滑體滑移特性影響

2.1 模型建立

非規則邊坡高位局部失穩滑動模型如圖6 所示，采用參數t控制坡面角大小。坡面角t取值為38.7°，滑面段水平距離為2 m，坡面段水平距離為6 m，水平段長度為15 m。滑面段上方設有由墻體單元圍成的矩形積土槽，用于生成并儲存滑體顆粒，將滑體儲存在簡單矩形（二維）或長方體（三維）積土槽中。在數值模擬中，將非規則邊坡高位處失穩滑體統一簡化為矩形，所有墻體單元均保持靜止不動。

圖6 非規則邊坡高位局部失穩滑移模型（單位：m）Fig.6 High-locality landslide model of irregular slope（unit:m）

生成的滑體模型如圖7 所示，滑體長為2.56 m，高為1.2 m，生成的土體顆粒充滿整個積土槽，顆粒總數為3 660 顆。為有效區分不同部位的滑體，在軟件中編寫命令語言，以矩形滑體形心為中心，將整個滑體平均分為4組，并以不同序號進行標記區分：上前部分滑體標為Ⅰ號，為第1 組；上后部分滑體標為Ⅱ號，為第2 組；下后部分滑體標為Ⅲ號，為第3組；下前部分滑體標為Ⅳ號，為第4 組。為選取滑體中具有代表性的顆粒進行分析，在矩形滑體的4個頂角處及中心位置，分別設置1個監測球，編號為1～5，用于監測該處顆粒的運動情況。

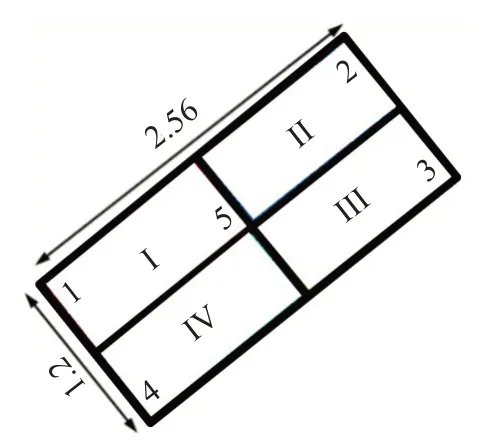
圖7 滑體分組及監測球布置示意（單位：m）Fig.7 Schematic diagram of sliding body grouping and monitoring ball arrangement（unit:m）

2.2 數值模擬

由于傅里葉描述因子D2、D3、D8對坡面幾何形貌具有不同控制作用，不同類因子的取值范圍不同，Di取值過大或過小都會使得幾何形貌失真，不符合實際情況。因此，在MATLAB 中生成大量的非規則幾何形貌邊坡，與實例的路基邊坡工程中的邊坡輪廓進行對比，經過多次試算與調整，使生成的非規則幾何形貌邊坡與實際自然邊坡輪廓相似，從而確定合理的Di取值范圍。其中，內摩擦角為5°～40°；坡面角為21.8°～90°；用于評判邊坡穩定性無量綱系數γH/c為10，γ為土體重度，H為邊坡高度，c為土體黏聚力；D2為0.100～0.280；D3為0.050～0.120；D8為0.007～0.021。

由確定的D2、D3、D8參數取值范圍，采用控制單一變量的方法，保持初相位為定值，確定模型中D2為 0.100 或 0.250，D3為 0.050 或 0.120，D8為0.007或0.020。當D2、D3、D8皆為0時，整個坡表變為直線型。

先將MATLAB 生成的邊坡輪廓數據點的坐標信息導入AutoCAD 中。再進行繪圖操作，生成相應邊坡輪廓圖形。然后，將生成的邊坡保存為dxf格式，導入PFC 2D 軟件之中。最后，進一步編寫命令生成組成積土槽的三面墻體，完成模型地建立。

將所有墻體摩擦系數設置為0，并在積土槽中生成滑體顆粒，初始顆粒之間接觸選用線性接觸，顆粒間摩擦系數為0，并賦予相應剛度，使生成的顆粒相互作用而彈開，最終充滿整個積土槽。當積土槽中顆粒穩定后，摩擦系數重新規定，顆粒間定為0.25，而顆粒與墻體之間定為0.40。對于黏性土，再一次賦予顆粒之間的接觸為平行黏結模型，對于無黏性土，顆粒之間仍保持線性模型不變。設置完接觸模型后需要對模型進行再一次平衡，得到最終平衡后的模型參數取值。球的粒徑比為1.50，密度為1 980 kg/m3；球-球的法向接觸剛度為3 000 kN/m，切向與法向剛度比為1，摩擦系數為0.25；墻的摩擦系數為0.40；黏結模型（接觸黏結）的法向黏結強度為5 000 Pa，切向黏結強度為5 000 Pa。

當滑體最終平衡之后，刪除作為積土槽的墻體單元，讓滑體在自重作用下變形解體，并沿著坡表向下運動，直到停止。

2.3 結果分析

為了研究坡面段幾何形貌對滑體運動軌跡的影響，在滑體中設置5個監測球，監測并分析滑體4 個頂點和中心顆粒在不同坡面段幾何形貌下的運動軌跡，每個編號顆粒的運動軌跡采用不同形式的軌跡線表示。

2.3.1 黏性顆粒的運動軌跡

直線型坡表中每個黏性顆粒的運動軌跡如圖8所示。從圖8 中可以看出，對于黏性滑體，編號1～5 的監測顆粒運動軌跡在直線型坡表呈現不同特征。3 號顆粒運動距離是最短的，表明：該處顆粒所受的阻力最大。1 號顆粒類似于拋物線型運動，表明：該顆粒沒有受到其他顆粒的相互作用，即該顆粒的黏結接觸破壞最早，隨后顆粒沿著坡表運動。從整體上看，位于滑體上部顆粒的運動距離遠大于位于底部顆粒的。

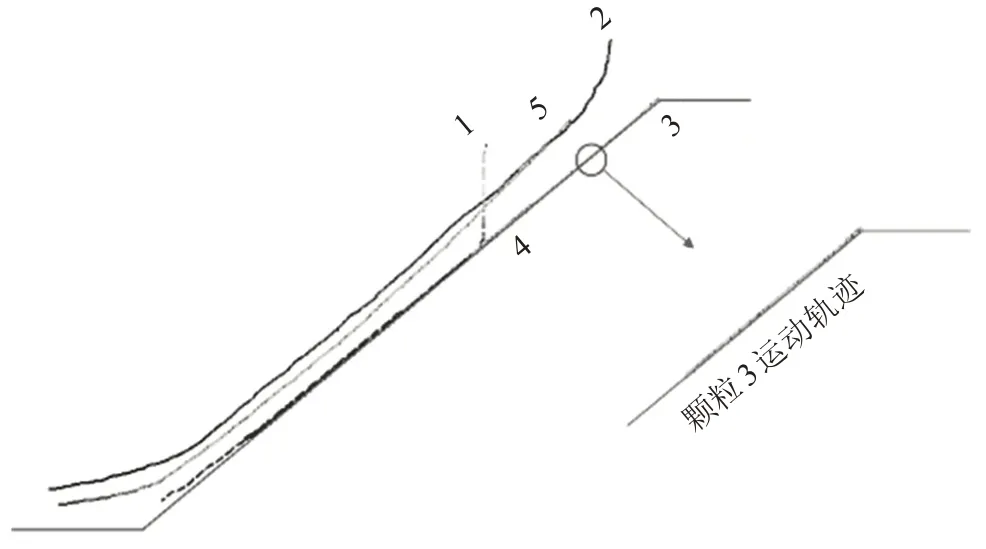
圖8 直線型坡表黏性顆粒運動軌跡Fig.8 Diagram of the movement trajectory of viscous particles on the straight slope surface

D2類坡表中每個黏性顆粒的運動軌跡如圖9所示。從圖9中可以看出，隨著D2的增大，監測顆粒的軌跡具有不同特征：4 號顆粒運動軌跡為均勻起伏型，D2越大起伏程度就越大；1 號顆粒先類似于拋物線型運動，然后與4 號顆粒一樣沿坡表運動；2 號和5 號顆粒在坡面段運動軌跡類似于均勻起伏型，但與4號顆粒相比，起伏程度較小，隨著D2的增大，起伏程度相應增大，相對于顆粒5平滑的運動軌跡，顆粒2的運動軌跡較為粗糙。

圖9 不同D2下黏性顆粒運動軌跡Fig.9 Diagram of movement trajectory of viscous particles under different D2 conditions

D3類坡表中每個黏性顆粒的運動軌跡如圖10所示。從圖10 中可以看出，隨著D3的增大，監測顆粒的軌跡具有不同特征：D3取值較小時（D3=0.05），4 號顆粒運動軌跡為非均勻起伏型，1 號顆粒先類似于拋物線型運動，隨后變為非均勻起伏型；2 號和5 號顆粒運動情況類似，與4 號顆粒相比，均為程度較小的非均勻起伏型，顆粒2運動軌跡略為粗糙；D3取值較大時（D3=0.12），某一特殊幾何形貌對顆粒運動軌跡影響較大，1 號顆粒做類拋物運動的距離增大，4 號顆粒在較大凹陷處運動軌跡脫離坡表，2 號和5 號顆粒在此處運動軌跡類似于直線型。

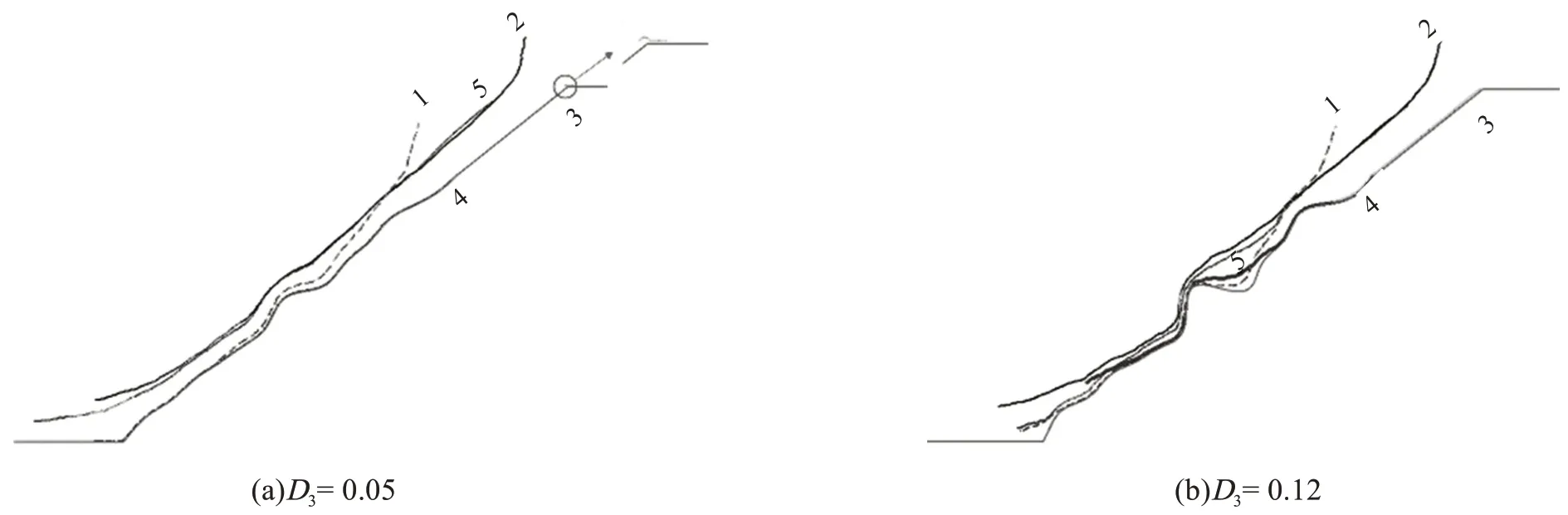
圖10 不同D3下黏性顆粒運動軌跡Fig.10 Diagram of movement trajectory of viscous particles under different D3 conditions

D8類坡表中每個黏性顆粒的運動軌跡如圖11所示，從圖11 可以看出，隨著D8的增大，監測顆粒的軌跡具有不同特征：當D8=0.02 時，4 號顆粒由于失穩時受到前方凸起坡表的影響，運動距離較短，最終停留在坡表凹陷處；1 號顆粒運動軌跡在坡面段為最小程度非均勻起伏型；2 號與5 號顆粒坡面段運動軌跡趨近于直線型，但2號顆粒軌跡線略微粗糙。

圖11 不同D8下黏性顆粒運動軌跡Fig.11 Diagram of movement trajectory of viscous particles under different D8 conditions

2.3.2 無黏性顆粒的運動軌跡

直線型坡表無黏性顆粒運動軌跡如圖12所示，與圖8對比可知，黏性與無黏性顆粒運動軌跡并無很大差異，但也有不同之處。無黏性1號顆粒停留在水平段，黏性1號顆粒停留在坡面段，前者運動距離更長；無黏性2 號顆粒的運動距離比黏性2 號顆粒的短。

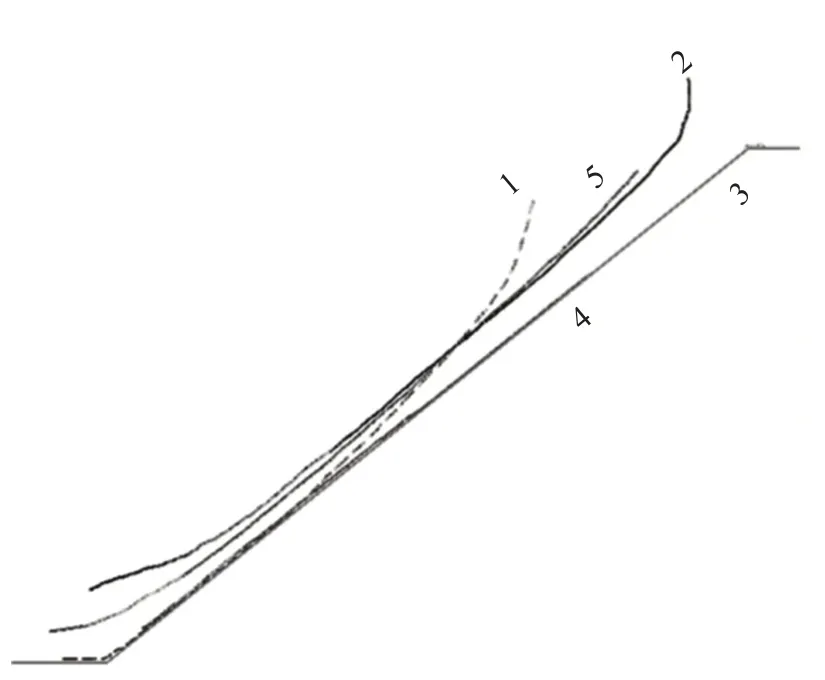
圖12 直線型坡表無黏性顆粒運動軌跡Fig.12 Diagram of the movement trajectory of non-viscous particles on the straight slope surface

D2類坡表無黏性顆粒運動軌跡如圖13 所示，與圖9對比可知，兩類監測顆粒運動軌跡相似，但也有不同之處。隨著D2的增大，黏性1號顆粒與無黏性1號顆粒之間的運動距離相差越來越小；黏性2 號顆粒與無黏性2 號顆粒運動距離之差隨著D2的增大而減小。當D2=0.2 時，兩類顆粒運動距離大致相同，無黏性1號顆粒運動軌跡隨著坡面均勻起伏程度的增大，而逐漸脫離坡表，在坡表上方運動。

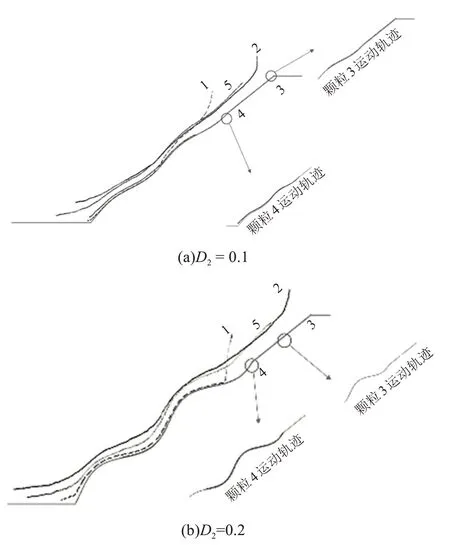
圖13 不同D2下無黏性顆粒運動軌跡Fig.13 Diagram of movement trajectory of non-viscous particles under different D2 conditions

D3類坡表無黏性顆粒運動軌跡如圖14 所示，對比圖10 可知，D3取值較小時（D3=0.05），兩類1號顆粒運動距離基本一樣。當D3取值較大時（D3=0.12），黏性1 號顆粒的運動距離明顯大于無黏性1號顆粒的，這與直線型和D2類坡表明顯不同。隨著D3的增大，兩類2 號顆粒運動距離相差越來越小。當D3=0.12 時，黏性2 號顆粒的運動距離反而大于無黏性2號顆粒的。當D3取值較大時，無黏性4 號顆粒由于特殊幾何形貌的影響，其運動距離明顯小于黏性4號顆粒的。

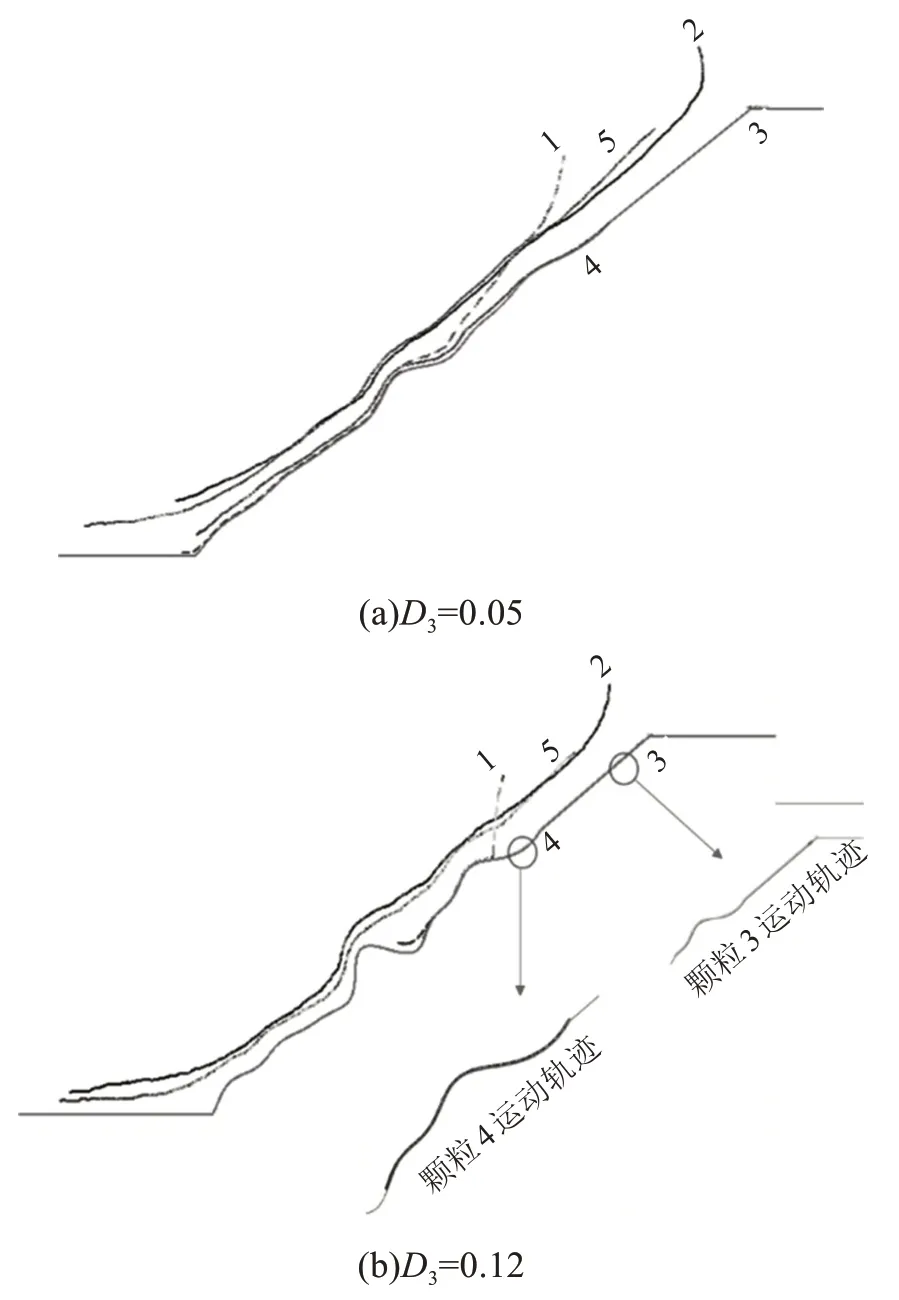
圖14 不同D3下無黏性顆粒運動軌跡Fig.14 Diagram of movement trajectory of non-viscous particles under different D3 conditions

D8類坡表無黏性顆粒運動軌跡如圖15 所示，對比圖11 可知，隨著D8的增大，兩類2 號顆粒運動距離之差逐漸減小。當D8=0.02 時，黏性與無黏性2 號顆粒運動距離大致相同。兩類1 號顆粒運動距離之差隨D8的增大而減小，最終趨近于0。

圖15 不同D8下無黏性顆粒運動軌跡Fig.15 Diagram of movement trajectory of non-viscous particles under different D8 conditions

對于黏性與無黏滑體，5 個監測顆粒運動軌跡在非規則坡表上各自特點：①當坡表為直線時，2號、4號、5號顆粒運動軌跡皆大致為直線，1號顆粒由于最先失穩且處于上前方，所以運動軌跡先為曲線型，再沿坡面運動成直線型。②當坡表為非規則幾何形貌時，對1 號、2 號、4 號、5 號顆粒運動軌跡有較大影響，而對運動距離很短的3號顆粒可以忽略。滑體上方的1 號、2 號、5 號顆粒的運動距離明顯大于位于底部4號顆粒的。

坡面幾何形貌對不同土類滑體的運動軌跡影響也不相同。對于D2類坡表，隨著D2取值的增大，無黏性1 號顆粒的運動距離逐漸趨近于1 號黏性顆粒的，2 號顆粒的運動規律也是如此，且無黏性1號顆粒隨著D2的增大而略微脫離坡表運動，這是由于無黏性土內部顆粒間沒有黏聚力，整體性較差導致的。對于D3類坡表，D3較小時，兩類顆粒運動距離基本相同，但繼續增大后，由于坡表存在較大凹陷與凸起處，導致黏性顆粒的運動距離將大于無黏性顆粒的。對于D8類坡表，當D8取值較大時，黏性與無黏性的1 號、2 號顆粒的運動距離大致相同。

3 結論

基于離散元軟件PFC 2D，對非規則邊坡高位滑體失穩模型進行數值分析，同時，基于離散傅里葉逆變換分析得到三類傅里葉描述因子Di對邊坡坡表幾何特征的影響規律，研究討論了不同傅里葉描述因子取值條件下的坡表輪廓對黏性與無黏性滑體失穩運動特性的影響，得到結論為：

1）整體分析表明，D2、D3、D8三類傅里葉描述因子不同取值形成不同類型的非規則坡面，而且坡面非規則幾何形貌對黏性與非黏性滑體的失穩運動特性都有明顯影響。

2）坡面非規則幾何形貌對下前方的4 號顆粒運動軌跡影響是最大的，1 號顆粒也受到坡面幾何形貌的影響，2 號、5 號顆粒運動軌跡受到坡面幾何形貌的影響相對較小，這是由于2 號、5 號顆粒所處位置較高且靠后的原因。因此，顆粒所處的位置越靠后、越高，其運動軌跡所受坡面幾何形貌的影響越小。

3）對于相同坡表，黏性與無黏性滑體內部5個監測顆粒運動軌跡相似，但也有部分差異。對于取值較大的D3與D8類坡表，某一特殊的幾何形貌出現在特定位置會對顆粒運動軌跡產生較大影響，而D2類坡表由于坡面幾何形貌均勻起伏，因此不會出現這種現象。