美英早期代數(shù)教科書中的一元二次不等式
狄 邁 (華東師范大學(xué)教師教育學(xué)院 200062)
1 引言
高考綜合改革制度下《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)(2017年版)》(下稱《標(biāo)準(zhǔn)》)將原課標(biāo)位于“必修五”的“不等式”置于必修模塊“主題一:預(yù)備知識(shí)”,要求幫助學(xué)生通過(guò)類比理解等式與不等式的異同,更進(jìn)一步地從函數(shù)觀點(diǎn)看一元二次不等式[1].在“雙新”背景之下,“一元二次不等式”作為初升高“預(yù)備知識(shí)”,正處于學(xué)生知識(shí)結(jié)構(gòu)銜接的核心地位,這時(shí)要幫助學(xué)生體會(huì)數(shù)學(xué)語(yǔ)言的抽象性以及思維方式從感性到理性的躍遷,使學(xué)生順利地跨越斷層,完成初高中數(shù)學(xué)學(xué)習(xí)的過(guò)渡.[2]
另一方面,《標(biāo)準(zhǔn)》重視數(shù)學(xué)文化的作用,提出“通過(guò)高中數(shù)學(xué)課程的學(xué)習(xí),認(rèn)識(shí)數(shù)學(xué)的科學(xué)價(jià)值、應(yīng)用價(jià)值、文化價(jià)值和審美價(jià)值”[1],數(shù)學(xué)不僅是一些知識(shí),而且是一種素質(zhì);當(dāng)然數(shù)學(xué)也不僅是一門科學(xué),更是一種文化;在“課程結(jié)構(gòu)”中指出,“把數(shù)學(xué)文化融入課程內(nèi)容中”.?dāng)?shù)學(xué)史是數(shù)學(xué)文化的重要組成部分.實(shí)踐表明,在數(shù)學(xué)教學(xué)中,數(shù)學(xué)史可以揭示知識(shí)之諧,呈現(xiàn)方法之美,營(yíng)造探究之樂(lè),達(dá)成能力之助,展示文化之魅,實(shí)現(xiàn)德育之效[3].
研究表明,對(duì)于剛學(xué)習(xí)不等式知識(shí)的學(xué)生來(lái)說(shuō),有較為明顯的歷史相似性[4].學(xué)生在求解一元二次不等式過(guò)程中常出現(xiàn)將解方程代替解不等式、將解方程方法遷移到不等式等錯(cuò)誤[5].考慮到學(xué)生的先驗(yàn)知識(shí),教師必須遵循教材編排順序進(jìn)行教學(xué),但是新入學(xué)的學(xué)生常會(huì)產(chǎn)生如下疑惑:等式與不等式在求解上有何異同?為何要用函數(shù)的方法對(duì)不等式進(jìn)行求解?不等式的各種求解方式有何聯(lián)系?為了回答這些問(wèn)題,我們對(duì)美英早期教科書中有關(guān)一元二次不等式的內(nèi)容進(jìn)行考察,以期從中獲取思想的啟迪,為教學(xué)提供有益的參考.
2 早期文獻(xiàn)中的不等式性質(zhì)
公元前3世紀(jì),古希臘數(shù)學(xué)家歐幾里得(Euclid)在《幾何原本》中提出公理——“整體大于部分”,在此基礎(chǔ)上,借助不等式的基本性質(zhì)證明了許多涉及不等關(guān)系的命題.
如卷一命題17:“任意一個(gè)三角形,其兩內(nèi)角的和總小于兩個(gè)直角.”歐幾里得的證明如下:如圖1,因∠ACD>∠ABC,故∠ACD+∠ACB>∠ABC+∠ACB,因此,∠ABC+∠ACB小于二直角.這里,歐幾里得運(yùn)用了不等式的性質(zhì):若x>y,則x+z>y+z.
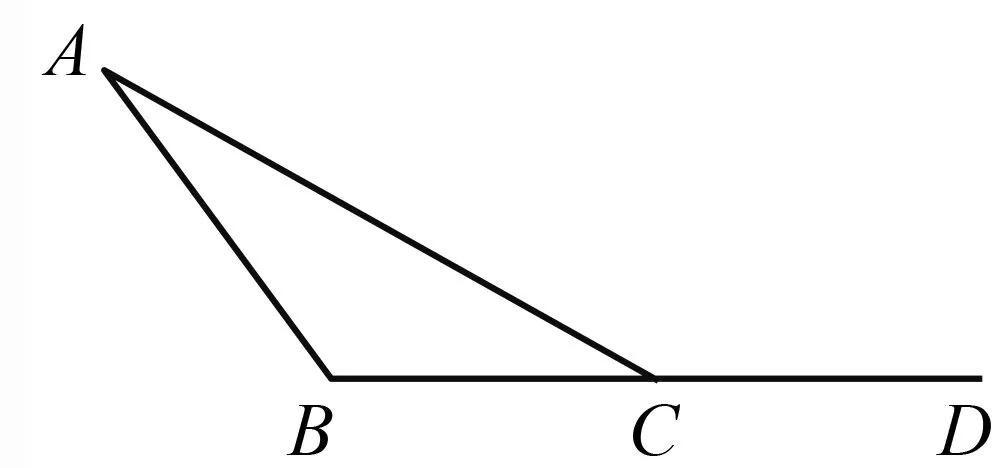
圖1
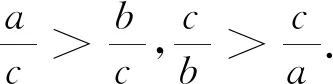
19世紀(jì)30年代,美英代數(shù)教科書中已經(jīng)出現(xiàn)了不等式(Inequality)及其簡(jiǎn)單的運(yùn)算規(guī)則.Davies總結(jié)了不等式的以下性質(zhì)[7]:
(1)在不等式兩端增加或減去相同的數(shù)量,所得到的不等關(guān)系不變.
(2)將相同意義(不等號(hào)相同)的兩個(gè)不等式兩端分別相加,所得到的不等關(guān)系不變.如,若a>b,c>d,e>f,則a+c+e>b+d+f;但兩端分別相減時(shí),結(jié)果不一定成立,如9>10,8>6,但9-8<10-6.
(3)不等式兩端同乘一個(gè)正數(shù),所得到的不等關(guān)系不變.如,由a>b可得3a>3b;不等式兩端同乘一個(gè)負(fù)數(shù),所得到的不等關(guān)系反向,如,由8>7,兩端同乘-3,得-24<-21.
(4)正數(shù)之間的不等式兩端各取平方值,不等關(guān)系不變.
(5)當(dāng)不等式兩端有一負(fù)數(shù)時(shí),無(wú)法在執(zhí)行運(yùn)算之前知道結(jié)果是什么.
該書對(duì)不等式的基本性質(zhì)進(jìn)行了介紹,指出不等式的變形與等式變形是類似的.
Edgerton等人敘述了不等式變形的七條法則,指出:若不等式兩端的值均為正,則兩端取相同次冪或相同次方根,不等關(guān)系不變,并且可以像等式那樣對(duì)不等式進(jìn)行變形[8].
我們看到,古希臘時(shí)期數(shù)學(xué)家借助幾何圖形得到不等式的基本性質(zhì).到后來(lái),數(shù)學(xué)家們均提出“像等式變形那樣,對(duì)不等式進(jìn)行變形”,所提出的變形規(guī)則也依據(jù)等式的變形規(guī)則而來(lái)再加以完善.換句話說(shuō),一切依賴于不等式變形的不等式求解,與其相應(yīng)的等式變形與求解過(guò)程是一體同心的.
3 一元二次不等式的求解
直到19世紀(jì)末,代數(shù)教科書中終于出現(xiàn)了一元二次不等式及其解法,其解法一定程度上借鑒了一元二次方程的求解方式.
3.1 配方法
與一元二次方程的情形類似,對(duì)于一元二次不等式,人們最先想到的解法也是配方法.但與方程情形不同的是,在求解不等式時(shí),人們并沒有借助于幾何圖形.
Smith給出了一元二次不等式的第一種解法——配方法[9].例如,對(duì)于不等式x2-4x+3>-1,將不等式左邊進(jìn)行配方,得x2-4x+3=(x-2)2-4+3.因此,不等式變?yōu)?x-2)2-1>-1,故得不等式的解集為{x|x∈R,且x≠2}.
Rouse也運(yùn)用配方法對(duì)一元二次不等式進(jìn)行求解[10].對(duì)于不等式k2-8k>0,不等式兩端分別加16,得到k2-8k+16>16,(k-4)2>16,由此可得k-4<-4,或k-4>4,于是得k>8或k<0.因此,不等式的解集為{k|k>8或k<0}.
Smith的例子較為特殊,經(jīng)移項(xiàng),不等號(hào)左邊原本就是完全平方,并且運(yùn)算大多涉及不等號(hào)左邊的恒等變形,并未脫離等式的配方法.Rouse運(yùn)用不等式的基本性質(zhì),通過(guò)不等號(hào)兩邊加上同一常數(shù)進(jìn)行配方,將等式的某些結(jié)論遷移至不等式,展現(xiàn)了不等式配方法本身的特點(diǎn).
3.2 因式分解法
歐拉(L. Euler, 1707-1783)在其《無(wú)窮分析引論》中指出,將整式函數(shù)分解成因式,其性質(zhì)就變得很明顯,一眼就可以看出變量取何值時(shí)函數(shù)值為零[11].通過(guò)因式分解,一元二次不等式也可以更直接地看出滿足要求的x的取值范圍.
Fisher 等人利用因式分解法來(lái)解一元二次不等式.例如,對(duì)于不等式x2+5x>-6,將-6移至左邊,得x2+5x+6>0,進(jìn)而得(x+2)(x+3)>0.為了使得(x+2)與(x+3)乘積為正,則兩個(gè)乘數(shù)需同時(shí)為正或同時(shí)為負(fù).當(dāng)x>-2時(shí),(x+2)與(x+3)同時(shí)為正;當(dāng)x<-3時(shí),兩者同時(shí)為負(fù).因此,滿足該不等式的x的取值范圍為x>-2或x<-3.[12]
可見,早期人們用因式分解法來(lái)解一元二次不等式時(shí),大多借助于代數(shù)運(yùn)算法則,通過(guò)因子相乘后的符號(hào)來(lái)推斷每一個(gè)因子的符號(hào),進(jìn)而得出x的取值范圍,是一種以代數(shù)為導(dǎo)向的求解方式.
Miller等人對(duì)于一元二次不等式的求解提出了三種不同方式,其中包括因式分解法[13].以不等式x2+x+6>0為例,將其寫成(x-2)(x+3)>0,根據(jù)乘積正負(fù)與因子正負(fù)的關(guān)系,得表1.

表1 (x-2)(x+3)正負(fù)與各因子正負(fù)的關(guān)系
20世紀(jì)初,教科書開始采用因式分解法來(lái)解一元二次不等式,通過(guò)乘積正負(fù)與因子正負(fù)的關(guān)系,判斷未知數(shù)x的取值范圍,隨后代入特殊數(shù)值加以檢驗(yàn).顯然,此時(shí)人們尚未將不等式與函數(shù)聯(lián)系在一起,而只局限于代數(shù)算法規(guī)則本身,自然不會(huì)出現(xiàn)利用圖象“穿針引線”的直觀方法.
3.3 求根法
求根法是指運(yùn)用一元二次方程的求根公式,先考察判別式Δ=b2-4ac的正負(fù)情況,若滿足Δ≥0,則求出對(duì)應(yīng)一元二次方程的根,再根據(jù)二次項(xiàng)系數(shù)a的正負(fù)性確定x的取值.
Hawkes在《高等代數(shù)》中首次借助一元二次方程,對(duì)一般的一元二次不等式解的情況進(jìn)行了討論.
當(dāng)一元二次方程ax2+bx+c=0(a≠0)有相同實(shí)根或虛根的時(shí)候,相對(duì)應(yīng)的一元二次不等式的符號(hào)取決于二次項(xiàng)系數(shù)a的符號(hào);如果方程有兩個(gè)不同的實(shí)根,x的取值介于兩根之間還是兩側(cè),也取決于系數(shù)a的符號(hào).具體如表2所示:
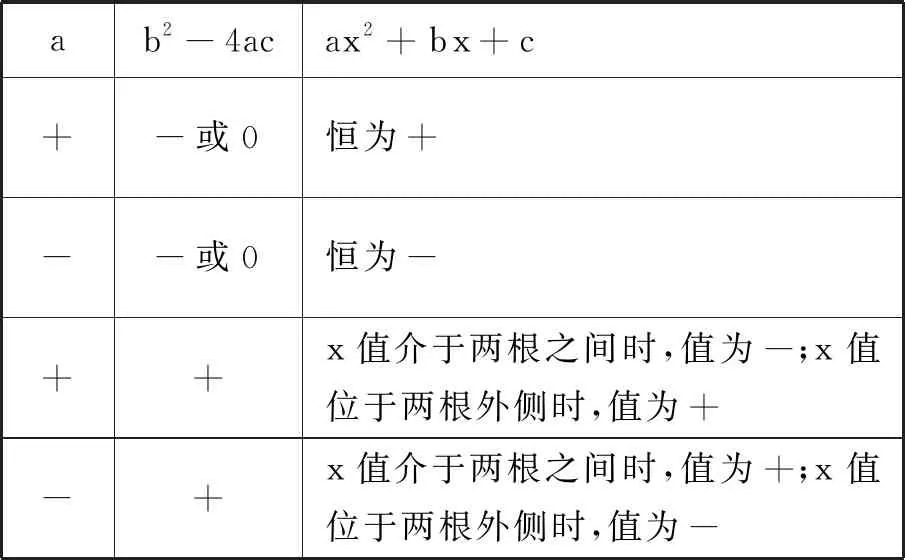
表2 Hawkes對(duì)一元二次不等式解的判斷[14]
明確將一元二次方程的根與一元二次不等式的解集聯(lián)系在一起,是這個(gè)時(shí)期教科書所實(shí)現(xiàn)的巨大飛躍,它與上文中的因式分解法的區(qū)別在于更加直接地肯定了求方程根的重要作用.可以說(shuō),求根法充分利用了一元二次方程本身的性質(zhì),從等式出發(fā)探索不等關(guān)系,將等式的相關(guān)知識(shí)與結(jié)論運(yùn)用于不等式.但是,教科書并未解釋清楚系數(shù)a的正負(fù)與x取值介于兩根之間抑或是兩側(cè)的關(guān)系,只是將它們之間的對(duì)應(yīng)關(guān)系進(jìn)行了簡(jiǎn)單的概括.
3.4 函數(shù)圖象法
函數(shù)思想在中學(xué)數(shù)學(xué)學(xué)習(xí)中占有重要地位.今日教科書中,解一元二次不等式的主流方法就是函數(shù)法.簡(jiǎn)單地說(shuō),函數(shù)法是指將原有一元二次不等式化為一元二次函數(shù),根據(jù)函數(shù)的性質(zhì)繪制相應(yīng)的函數(shù)圖象,通過(guò)數(shù)形結(jié)合得到未知數(shù)取值范圍的方法.
Hedrick首次借助函數(shù)圖象解決不等式問(wèn)題,總結(jié)出一元二次方程的根、其代表的函數(shù)圖象與不等式解集之間的關(guān)系.
以不等式x2+2x-8>0為例,求解滿足該不等式的未知數(shù)x的取值范圍.首先,令l(x)=x2+2x-8>0,繪制其圖象(圖2).可以得出,l>0等價(jià)于函數(shù)圖象位于x軸上方,當(dāng)x取值位于x= -4左側(cè)或x=2右側(cè)時(shí)成立.x=-4與x=2兩個(gè)實(shí)數(shù)點(diǎn)可以通過(guò)解方程l(x)=0,即x2+2x-8=0得到.類似地,方程x2+2x-8=0的兩個(gè)根分別為x1=-4,x2=2,由圖得出,滿足不等式x2+2x-8<0的x的值介于兩根x1=-4,x2=2之間,即-4 圖2 l(x)的圖象 Hedrick指出:類似地,在任何情況下,我們都可以用圖象表示不等號(hào)的左右兩側(cè),看看何時(shí)一方超過(guò)另一方.從圖上可以明顯地看出,我們首先應(yīng)該找出當(dāng)兩邊相等時(shí),使得其成立的點(diǎn)就是兩個(gè)圖象的交點(diǎn)[15]. Hedrick的方法點(diǎn)明了不等式中“相等”的重要性,“相等”是“不等”的邊界.另外,此種借助圖象來(lái)求解一元二次不等式的方式不局限于一元二次不等式,還可以推廣到任何不等式的求解.通過(guò)移項(xiàng),繪制不等式兩側(cè)代數(shù)式所代表的函數(shù)的圖象,觀察比較兩側(cè)函數(shù)值的大小,得到對(duì)應(yīng)的自變量x的取值范圍就是不等式的解集.在該書中,作者雖用函數(shù)的圖象來(lái)求解不等式,也沒有明確提及用函數(shù)來(lái)解決不等式的問(wèn)題,但是其中蘊(yùn)含了今日的函數(shù)思想. Edgerton等人明確提出用函數(shù)來(lái)解不等式:將不等式進(jìn)行移項(xiàng),左邊的代數(shù)式轉(zhuǎn)化為函數(shù)f(x),繪制函數(shù)圖象,當(dāng)函數(shù)圖象位于x軸上方時(shí),函數(shù)值為正,即滿足不等式f(x)>0[8]. Davis給出了一般一元二次不等式的函數(shù)解法.對(duì)于一般一元二次不等式ax2+bx+c>0 (其中a,b,c均為常數(shù),若不等號(hào)為“<”則兩端同乘-1,得到“>”),我們繪制以x為自變量的函數(shù)y=ax2+bx+c的圖象.如果函數(shù)圖象全部位于x軸上方,那么不等式ax2+bx+c>0對(duì)于一切x均成立;相反地,如果函數(shù)圖象全部位于x軸下方,那么不等式對(duì)于任何x都不成立,即無(wú)解.如果介于中間的情況,有部分值滿足y>0這一條件.顯而易見的是,滿足條件的x的值介于一元二次方程ax2+bx+c=0的兩根之間,或小于較小的根、大于較大的根[16]. 至此,一元二次不等式與函數(shù)終于難舍難分,此后幾乎所有有關(guān)一元二次不等式的求解均會(huì)提到“函數(shù)圖象解法”. Hart將函數(shù)解法稱為“不等式的圖象解法”,將求解的重點(diǎn)放于對(duì)函數(shù)圖象的觀察與解釋.他指出:一元不等式可以通過(guò)變形化為f(x)>0或f(x)<0的形式.對(duì)變形后的不等式的求解步驟為:(1)畫出函數(shù)f(x)的圖象;(2)使得f(x)圖象位于x軸上方的x的取值,即為滿足不等式f(x)>0的x的取值;使得f(x)圖象位于x軸下方的x的取值,即為滿足不等式f(x)<0的x的取值[17]. 根據(jù)早期代數(shù)教科書中相關(guān)敘述,以20年為一單位,呈現(xiàn)了“一元二次不等式”求解方法的演進(jìn)過(guò)程(圖3). 圖3 求解方法演進(jìn)過(guò)程 早期一元二次不等式的求解方式呈現(xiàn)出由單一走向多樣,最后回歸單一的趨勢(shì). 20世紀(jì)前,人們單純將等式求解遷移到不等式,“配方法”是求解一元二次不等式的主流.20世紀(jì)初,“函數(shù)圖象法”出現(xiàn),在后續(xù)的幾十年中迅速占據(jù)重要地位,究其原因,其一,分析理論的逐漸完善促進(jìn)了“函數(shù)思想”的發(fā)展;其二,20世紀(jì)初,F(xiàn).克萊因(F.C. Klein, 1849—1925)提出了“米蘭大綱”,發(fā)表自己對(duì)數(shù)學(xué)教育的看法,主張“函數(shù)是中學(xué)數(shù)學(xué)教育的基石”,加強(qiáng)函數(shù)思想的教學(xué),使得函數(shù)在數(shù)學(xué)課程之中地位提高. 綜上所述,歷史上出現(xiàn)了一元二次不等式的多種求解方法,為今日不等式教學(xué)提供了諸多啟示. 其一,注重知識(shí)之間的普遍聯(lián)系.在早期教科書對(duì)于“一元二次不等式”的求解過(guò)程中,表現(xiàn)出對(duì)“方程思想”“函數(shù)思想”的運(yùn)用;某些教科書習(xí)題[18]中也將行列式的計(jì)算與不等式的求解聯(lián)系在一起,溝通不等式與其他數(shù)學(xué)知識(shí).因此,在復(fù)習(xí)課中,可以基于“一元二次不等式”設(shè)計(jì)問(wèn)題串,使用“1+X”教學(xué)模式,將不等式與方程、函數(shù)、解析幾何等知識(shí)聯(lián)系在一起,形成知識(shí)網(wǎng)絡(luò),構(gòu)建知識(shí)之諧,展現(xiàn)方法之美. 其二,嘗試跨學(xué)科教學(xué).跨學(xué)科學(xué)習(xí)可以幫助學(xué)生在學(xué)習(xí)某一學(xué)科知識(shí)時(shí),從促進(jìn)知識(shí)的理解起步,再到對(duì)知識(shí)或?qū)W科內(nèi)容的個(gè)性化建構(gòu),然后能結(jié)合實(shí)際中的生活問(wèn)題進(jìn)行創(chuàng)新或創(chuàng)造[19].Rouse基于物理中的“上拋運(yùn)動(dòng)”[10]設(shè)計(jì)了“一元二次不等式”的相關(guān)問(wèn)題,將其與物理、實(shí)際生活聯(lián)系在一起.在教學(xué)過(guò)程中,教師可以基于該知識(shí)設(shè)計(jì)項(xiàng)目式學(xué)習(xí)活動(dòng),尋找生活中的“一元二次不等式”,溝通數(shù)學(xué)與現(xiàn)實(shí),打破學(xué)科之間的壁壘,使數(shù)學(xué)真正地服務(wù)于生活,讓學(xué)生體會(huì)數(shù)學(xué)文化. 其三,通過(guò)技術(shù)實(shí)現(xiàn)由靜到動(dòng)的轉(zhuǎn)變.中國(guó)教育信息化已步入了融合創(chuàng)新、智能引領(lǐng)的新時(shí)代——教育信息化2.0 時(shí)代[20].當(dāng)下需要實(shí)施能有效變革課堂教學(xué)結(jié)構(gòu)的創(chuàng)新教學(xué)模式[21],發(fā)展與深入研究適合學(xué)科的信息技術(shù),促進(jìn)學(xué)生的認(rèn)知與交流.高一學(xué)生對(duì)“函數(shù)”的認(rèn)識(shí)多停留于靜態(tài),其與“不等式”的聯(lián)系重點(diǎn)是“動(dòng)態(tài)”的實(shí)現(xiàn).因此,教師可通過(guò)幾何畫板的動(dòng)態(tài)展示,引導(dǎo)學(xué)生自主地將二次函數(shù)與方程、不等式的解聯(lián)系在一起,從具體的動(dòng)畫中抽象出數(shù)學(xué)概念,實(shí)現(xiàn)能力之助. 其四,比較方程與不等式的異同.學(xué)生由初中到高中,解不等式的過(guò)程中常常會(huì)“生搬硬套”,產(chǎn)生負(fù)遷移.早期教科書中所說(shuō)的“像求解等式那樣求解不等式”[7],或許也是造成某些錯(cuò)誤的一部分原因.現(xiàn)行教學(xué)中也多出現(xiàn)方程與等式對(duì)等的情況,這常常使得學(xué)生將等式(方程)求解過(guò)程直接遷移至不等式,因此在教學(xué)過(guò)程中,教師有必要強(qiáng)調(diào)方程與不等式的異同.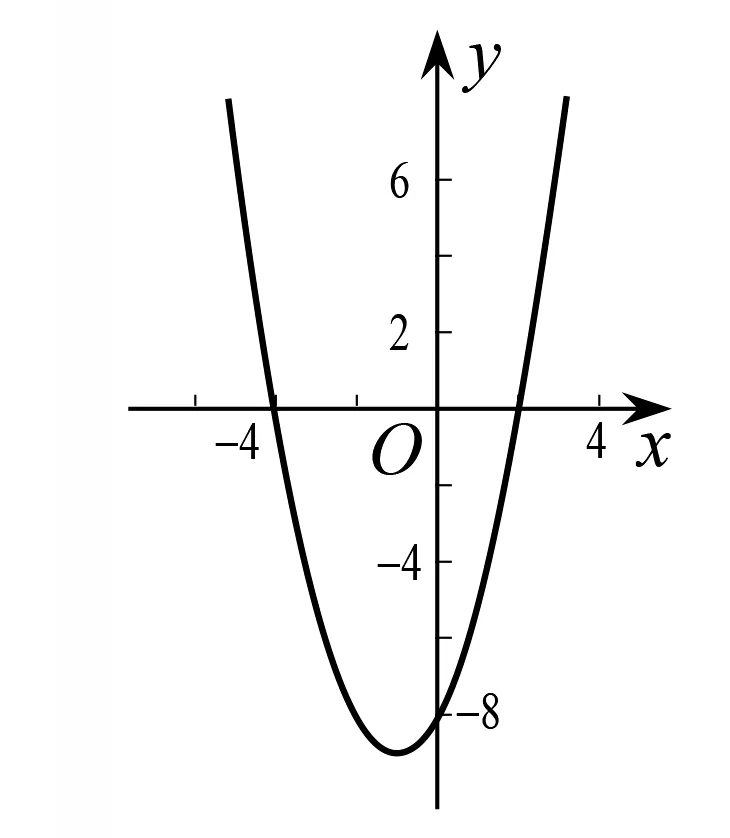
4 一元二次不等式求解方法的演變
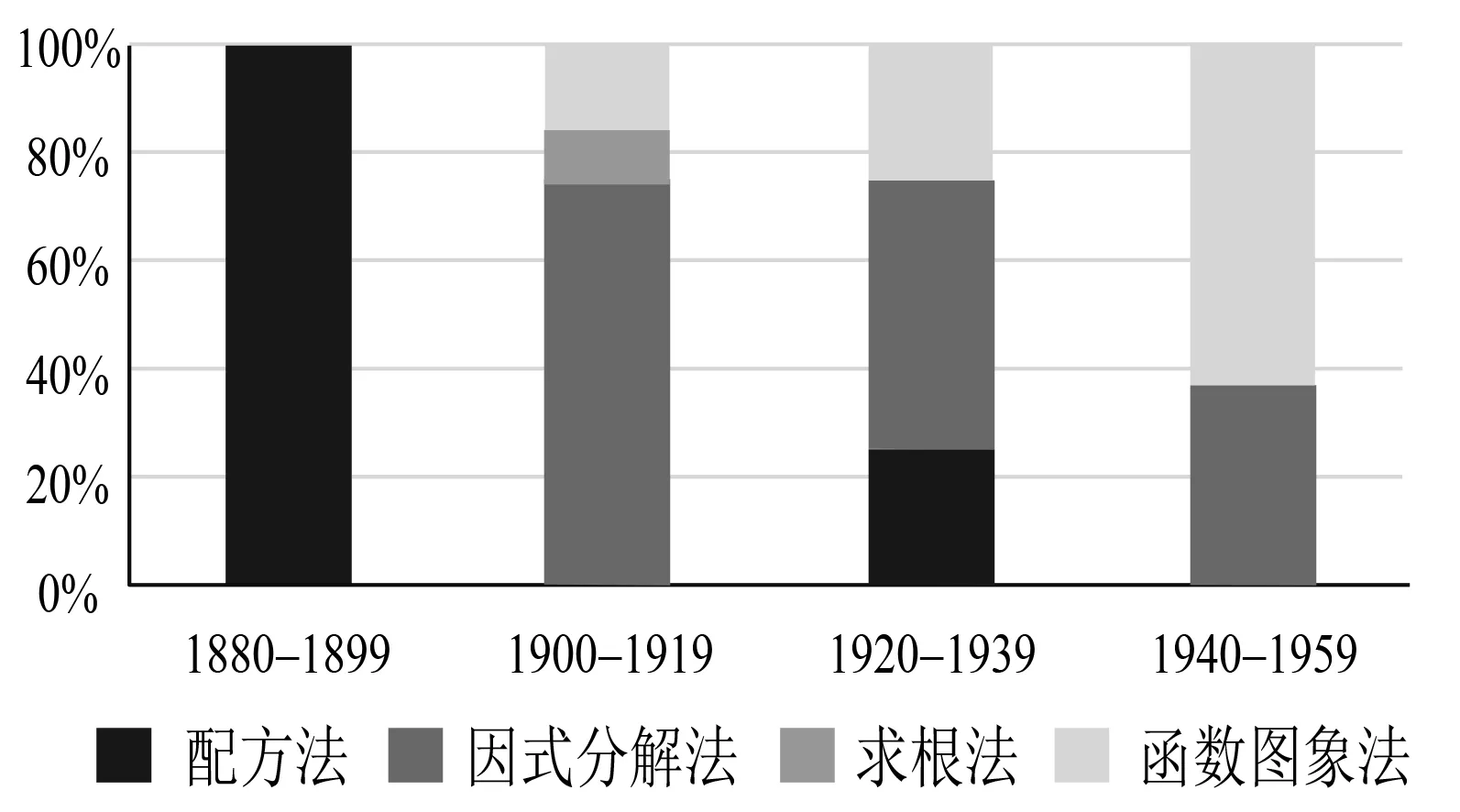
5 教學(xué)啟示
- 中學(xué)數(shù)學(xué)雜志的其它文章
- 中國(guó)數(shù)學(xué)教育研究的現(xiàn)實(shí)圖景與未來(lái)道路
——聚焦國(guó)內(nèi)同行對(duì)ICME-14的學(xué)術(shù)貢獻(xiàn) - 基于數(shù)學(xué)運(yùn)算素養(yǎng)的一道聯(lián)考題的思考
- 探究構(gòu)圖 優(yōu)化路徑 提升素養(yǎng)
——記一道解析幾何題的求解歷程 - 追本溯源 深度思維
——對(duì)一道中考模擬壓軸題的思考 - “爬樓梯車輪支架旋轉(zhuǎn)半徑的優(yōu)化設(shè)計(jì)”辨析
- 高中數(shù)學(xué)跨學(xué)科教學(xué)的實(shí)踐
——以數(shù)學(xué)與人文學(xué)科的融合為例*

