Soliton molecules and asymmetric solitons of the extended Lax equation via velocity resonance
Hongcai Ma(馬紅彩) Yuxin Wang(王玉鑫) and Aiping Deng(鄧愛平)
1Department of Applied Mathematics,Donghua University,Shanghai 201620,China
2Institute for Nonlinear Sciences,Donghua University,Shanghai 201620,China
Keywords: the extended Lax equation,soliton molecules,velocity resonance mechanism
1. Introduction
In recent years,there has been a growing number of publications focusing on soliton molecules. Soliton molecules as localized nonlinear waves were proposed by Akhmediev in 2000.[1]In some fields, soliton molecules have been observed experimentally.[2-6]First of all, in a dispersionmanaged optical fiber,soliton molecules were firstly observed in experiments.[2]As a kind of local nonlinear waves in the fields of physics, solitons have exhibited bound states, which are similar to molecules including optics,[7]plasma physics,[8]fluid dynamics,[9]gravity,[10]and so forth. Recent work by Herinket al.[11]has settled the evolution of femtosecond soliton molecules in the cavity of a several period mode-locked laser with the help of a novel time-stretch technique. The authors in Ref. [11] examined the existence state and two- and three-soliton stability of bound states in a dispersion managed fiber in 2013.
Recently, one of the most important events of the soliton molecules was that in Refs. [12,13], the authors theoretically obtained the three kinds of (1+1)-dimensional soliton molecules and asymmetric solitons using velocity resonance for the first time in 2019, including the fifth-order Korteweg-de Vries(KdV)equation,the Sawada-Kotera(SK)equation and the Kaup-Kupershmidt equation. The authors in Ref.[14]resolved soliton molecules,asymmetric solitons and mixed solutions for(2+1)-dimensional fifth-order KdV equation in 2019. These trends in velocity resonance of the soliton molecules have led to a proliferation of research. For example, in 2020, Yanet al.[15]investigated the breathing soliton molecules, kink molecules and half periodic kink molecules of the(1+1)-dimensional Sharma-Tasso-Olver-Burgers equation. Based on theN-soliton solution,Yanget al. have investigated several fresh molds of mixed solutions which are made up of soliton molecules, breather waves and lump waves of the (2+1)-dimensional BKP equation[16]using velocity resonance method, module resonance method and long wave limit method. Yanget al. also investigated soliton molecules andN-order smooth position solutions for the Gerdjikov-Ivanov equation.[17]Meanwhile, based on theN-soliton solutions, some new types of mixed solutions to the (2+1)-dimensional bidirectional SK equation[18]are generated in the same way. After that, Maet al.obtained soliton molecules and several new mixed solutions for some(2+1)-dimensional equations.[19,20]Therefore,we will get round to consider other integrable equations. Then we make great efforts to seek out the soliton molecules, asymmetric solitons and the interaction between solitons and soliton molecules(or the interaction between solitons and asymmetric solitons). It is noteworthy that Ma gave a universal study onN-soliton solutions and the Hirota conditions for(1+1)-dimensional equations[21]and for(2+1)-dimensional equations.[22]As a rare example,a new example in(2+1)-dimensions was presented in Ref.[23].
The aim of this paper is to examine the soliton molecules of the extended Lax equation[24]
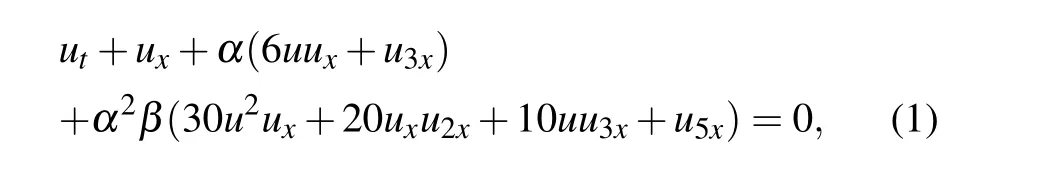
whereα ?1 is a non-dimensional measure of the small wave amplitude related to depth, andβis the coefficient of the higher-order terms. Compared with the Lax equation,the the extended Lax equation is constituted of the two linear dispersive termsu3xandu5xas well as four nonlinear terms. It is obvious that the extended Lax equation is derived from the extended KdV equation.The issue if the extended KdV equation is integrable was further discussed in Refs.[25-29]. In 2016,Wazwaz[24]used the simplified Hirota method to officially obtain multiple soliton solutions of the extended Lax equation.However, soliton molecules, asymmetric solitons and the interaction between solitons and soliton molecules of the extended Lax equation have not been investigated. Therefore,the primary aim of this paper is to critically analyze the soliton molecules, asymmetric solitons and the interaction between solitons and soliton molecules of the extended Lax equation.
The remaining part of the paper proceeds as follows:In Section 1, we study the extended Lax equation’s soliton molecules based onN-soliton formula and the interactions between solitons and soliton molecules using the method of velocity resonance. In Section 3,we derive the asymmetric soliton of the extended Lax equation by properly setting parameters’constraints for soliton molecules. In Section 4,we give a brief summary and critique of the findings.
2. Solitons and soliton molecules of the extended Lax equation
N-soliton solutions to Eq.(1)can be written as[24]

On the basis of this resonant condition(8), by combining theith andjth solitons,a soliton molecule can be constructed according to the choice of the solution parameters.
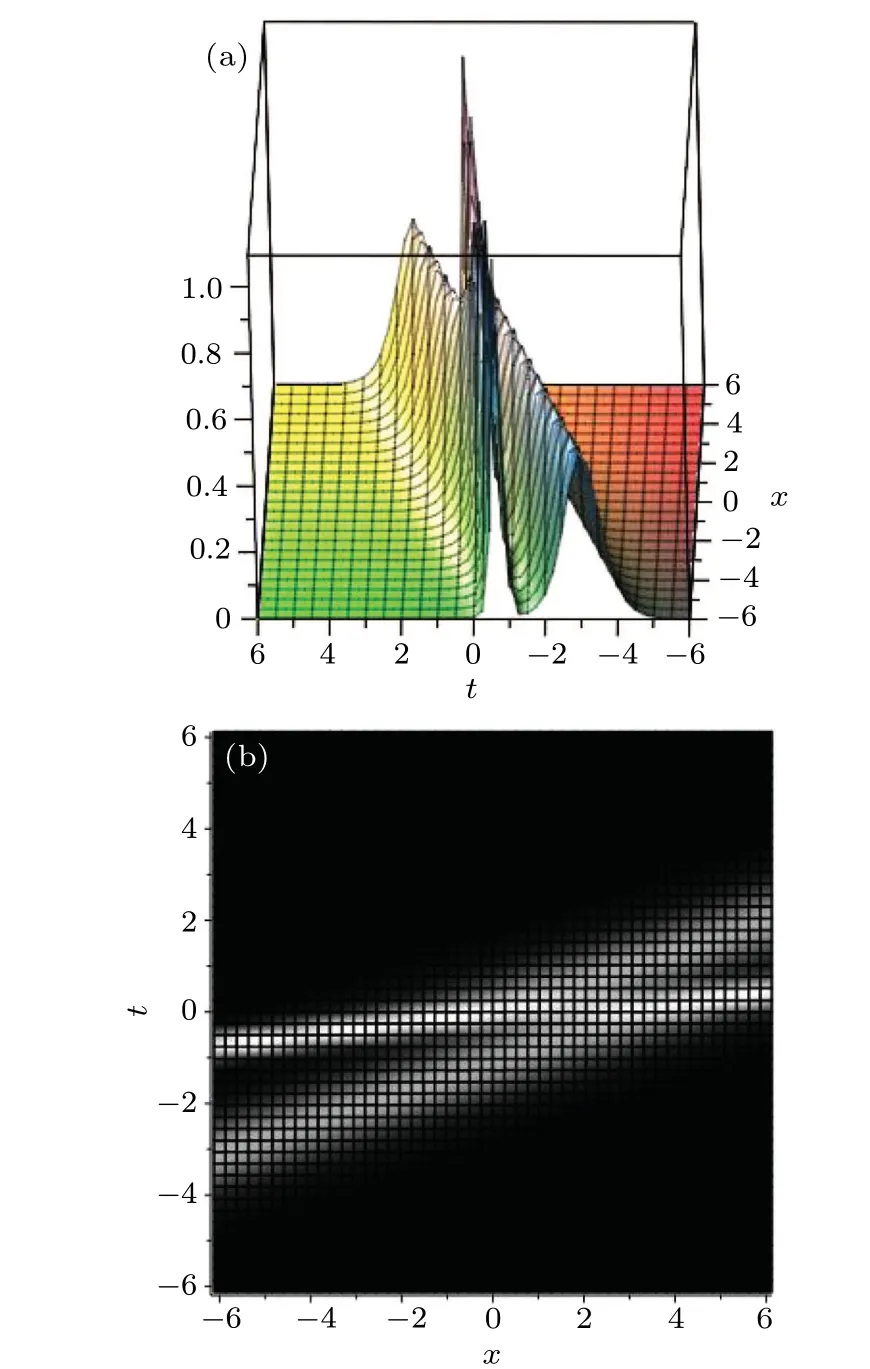
Fig.1.(a)The 3D diagram of the two-soliton solution u(x,t)for k1=1,k2=1.5,α =1,β =1. (b)The density diagram of the two-soliton solution u(x,t)with the same parameters.
In order to show this phenomenon more and more intuitive, let us takeN= 2 as an example to conduct a study.On the basis of the resonant condition (8), the two solitons forN=2 in Eqs. (3)-(6) are bounded to generate a soliton molecule. Figure 2 shows a soliton molecule where the parameters are fixed as

From Fig. 2(a), we can observe that two solitons in the molecule are not the same due tok1/=k2even though their velocities are same. Moreover, we can find that the selection of parameterφdetermines the distance between soliton molecules. When the two peaks of soliton molecules are close enough,the soliton molecule seems to become one soliton,we will call this kind of soliton molecule an asymmetric soliton.Hence,an asymmetric soliton solution can be generated from the soliton molecule by choosing the appropriate parameterφ.In order to show this phenomenon more intuitively,the author is going to set the same parameters as used in Fig.2,except to changeφ2to-1. What can be clearly seen in Fig. 3 are the plots of the asymmetric soliton.
For the three-soliton solution to the extended Lax equation, the three-soliton solution to Eqs. (3)-(6) are shown in Fig. 4. Moreover, we will set up the interaction solutions between a two-soliton molecule and a common soliton. The three-soliton solution will become an interaction solution between a soliton molecule and a soliton if two solitons are bounded together to form a soliton molecule. A special interaction solution between a common soliton and a soliton molecule is depicted in Fig.5,where the parameters are fixed as

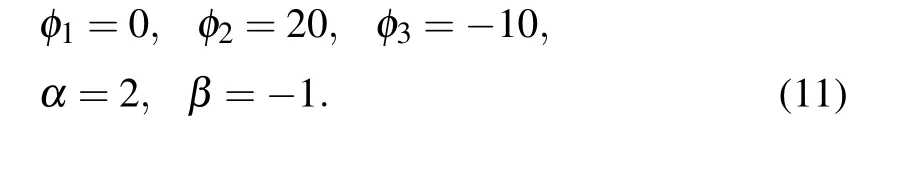
It can be seen from the above discussion that when the distance of peaks between two solitons in the soliton molecule is small enough,that is,by changing theφ2value,the soliton molecule can be converted into an asymmetric soliton. Figure 6 shows the interaction between an asymmetric soliton and a soliton by changing theφ2from 20 to-5.
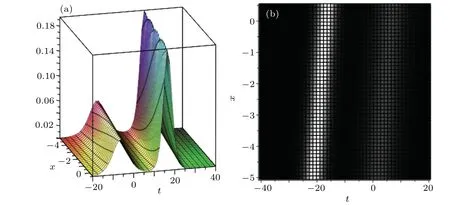
Fig.2. Soliton molecule structure of Eq.(1)with the parameters set as in(10): (a)3D diagram,(b)density diagram.

Fig.3. Asymmetric soliton of Eq.(1)with the parameters set in(10)but φ2=-1: (a)3D image,(b)2D image.

Fig.4. The three-soliton solution u(x,t)for k1=1,k2=1.2,k3=1.4,α =1,β =1: (a)3D diagram,(b)density diagram.
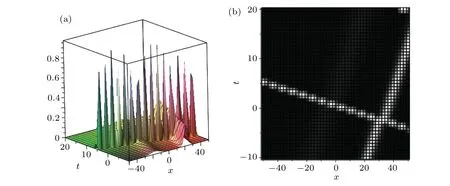
Fig.5.Special interaction solution between a common soliton and a soliton molecule of Eq.(1)with the parameters set as(11):(a)3D diagram,(b)density diagram.
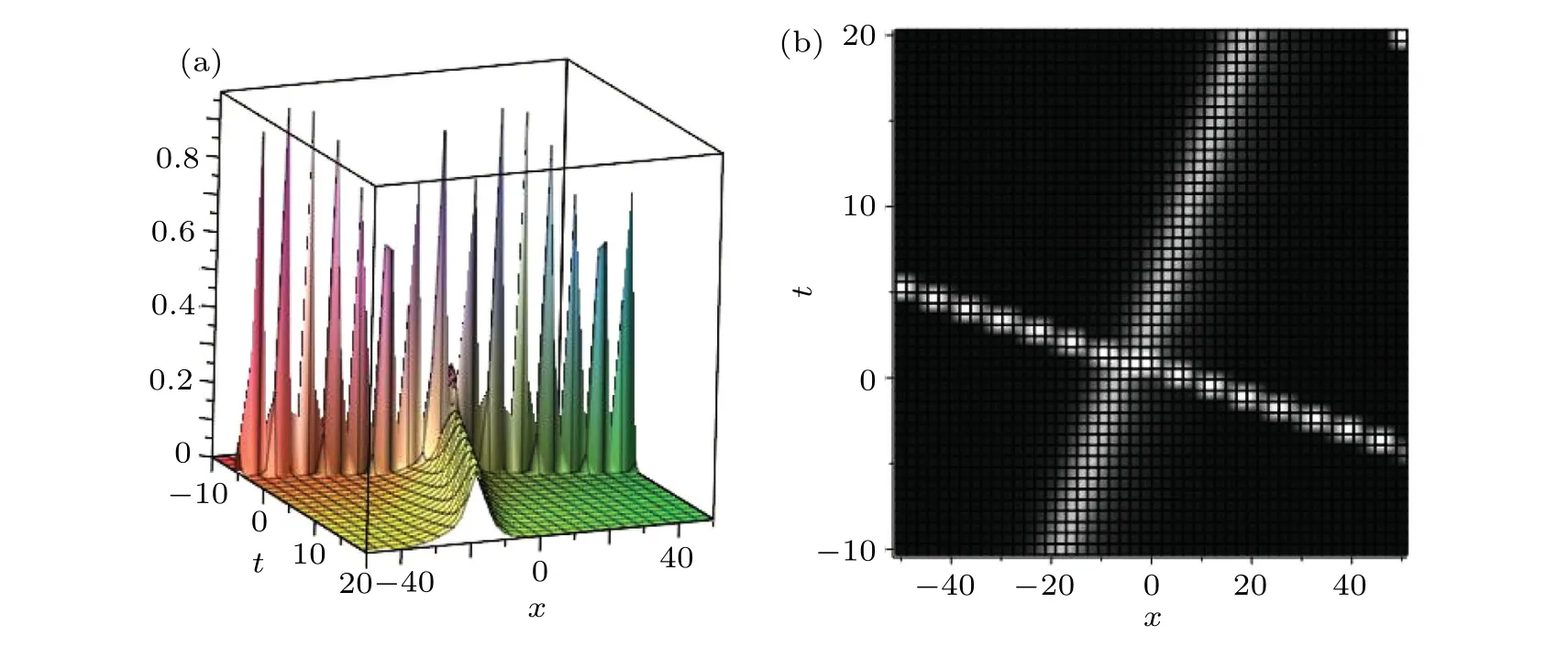
Fig. 6. The interaction solution among a single-soliton solution and an asymmetric soliton: (a) 3D diagram, (b) density diagram, (a) 3D diagram,and(b)density diagram.
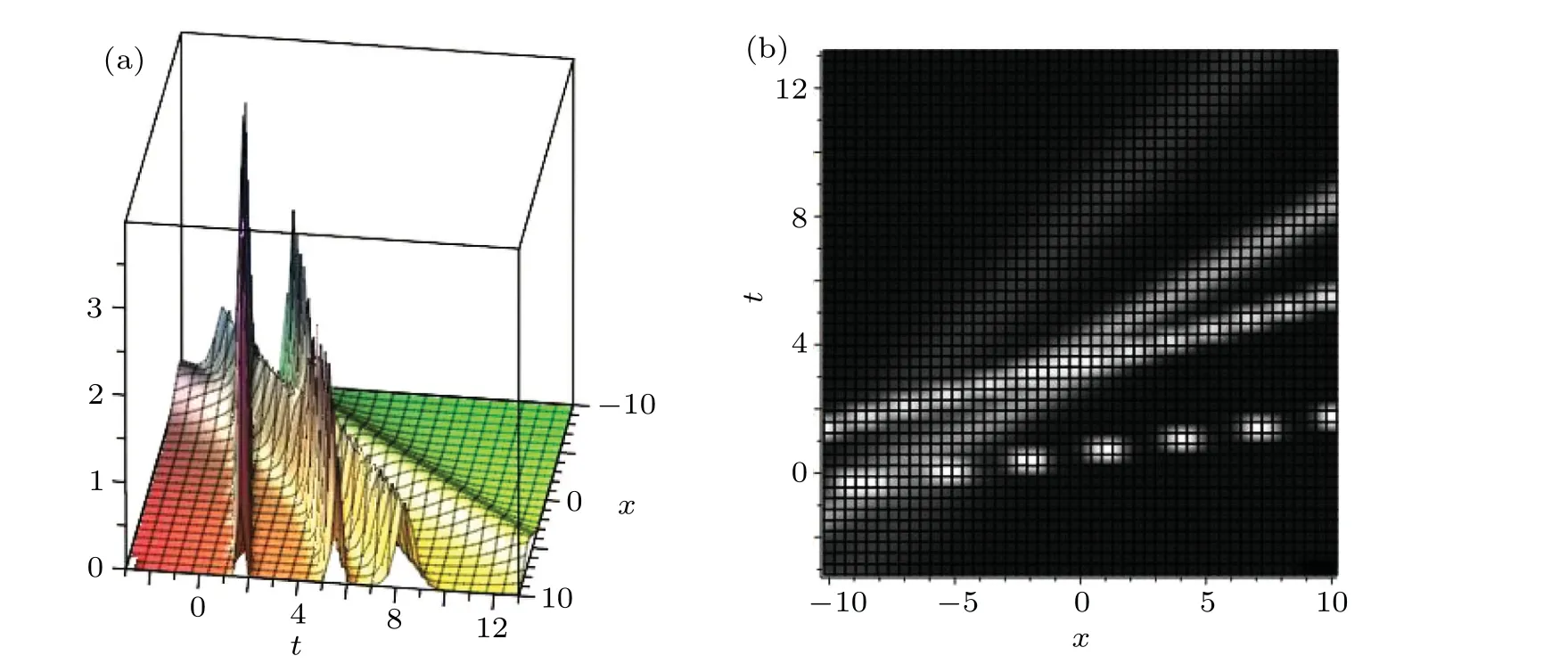
Fig. 7. The four-soliton solution u(x,t) for k1 =1, k2 =2, k3 =3, k4 =4, α =1/4, β =1/4, φ1 =10, φ2 =20, φ3 =50, φ4 =30: (a) 3D diagram,(b)density diagram.
In the following,we consider the condition ofN=4,the four-soliton solution of Eqs.(3)-(6)can be obtained. Figure 7 presents the structure of its four-soliton solution.Furthermore,we can also construct the interaction solutions between a soliton molecule and a two-soliton solution. If two solitons are combined into a soliton molecule, the four-soliton solution will turn into an interaction solution among a two-soliton solution and a soliton molecule.Figure 8 presents the interaction solution between a two-soliton solution and a soliton molecule where the parameters are fixed as
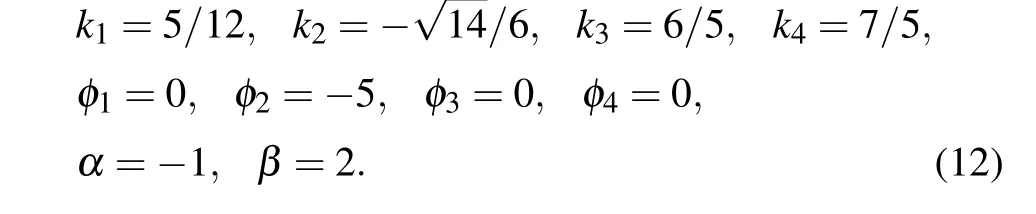
Accordingly, we can infer that four-soliton solution can produce two soliton molecules;kiandci(i=1,2,3,4)satisfy Eq.(5). Figure 9 shows the property of the interaction for the extended Lax equation withN=4 and with parameters

Not only can we construct two soliton molecules from four-soliton solution,but also we can transform these two soliton molecules into two asymmetric solitons via changing the value ofφ. Looking at Fig.10,it is apparently shown that the interaction between two asymmetric solitons with the parameters(13)butφ2=5-13 andφ3=10-5.
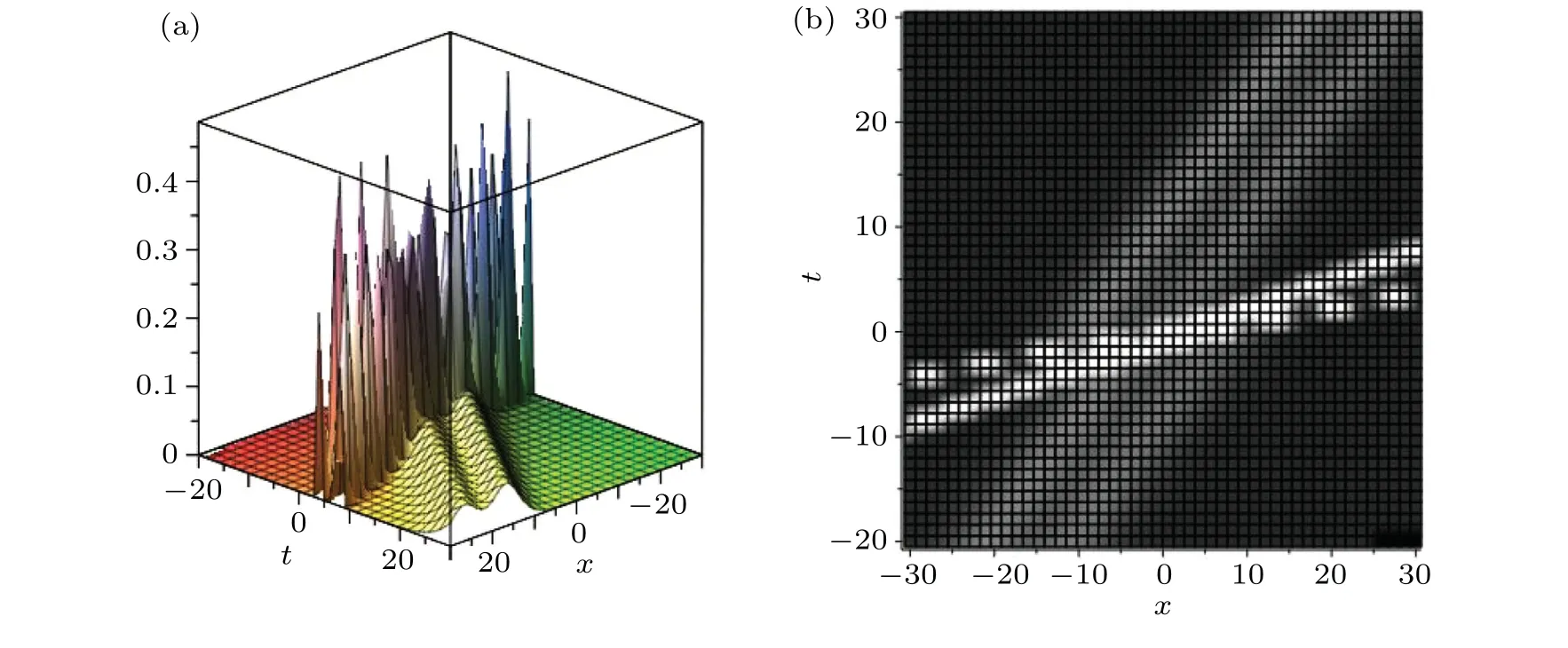
Fig.8. The interaction solution between a two-soliton solution and a soliton molecule: (a)3D diagram,(b)density diagram.

Fig.9. Two-soliton-molecule structure for Eq.(1)with N=4 and(13): (a)3D image,(b)density diagram.
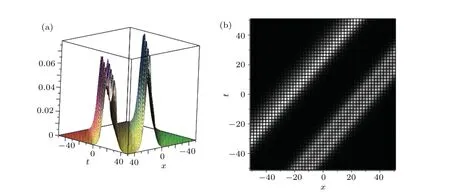
Fig.10. Two-asymmetric-soliton structure for Eq.(1): (a)3D image,(b)density diagram.
3. Conclusion
This study set out to use a new method for investigating soliton molecules,asymmetric solitons,the interaction solution between solitons and soliton molecules(or asymmetric soliton),the interaction between two soliton molecules(or between two asymmetric solitons by setting the appropriateφ)of the extended Lax equation. Meanwhile, we display some related pictures as mentioned above of these solutions. It is worth noting that the velocity resonance leads to theN-wave solution to traveling wave solutions,so it can generate a kind of special solutions. The interaction solutions are long-wave limits ofN-soliton solutions or envelop solutions ofN-soliton solutions.Therefore,it is worth studying the Hirota conditions for nonlinear equations. We hope that the results of this paper can provide valuable information about the study of mathematical physics.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant Nos. 11371086, 11671258, and 11975145),the Fund of Science and Technology Commission of Shanghai Municipality, China (Grant No. 13ZR1400100),the Fund of Institute for Nonlinear Sciences, Donghua University, and the Fundamental Research Funds for the Central Universities,China(Grant No.2232021G-13).
- Chinese Physics B的其它文章
- Role of compositional changes on thermal,magnetic,and mechanical properties of Fe–P–C-based amorphous alloys
- Substrate tuned reconstructed polymerization of naphthalocyanine on Ag(110)
- Anti-PT-symmetric Kerr gyroscope
- Information flow between stock markets:A Koopman decomposition approach
- Cascading failures of overload behaviors using a new coupled network model between edges
- High efficiency ETM-free perovskite cell composed of CuSCN and increasing gradient CH3NH3PbI3

