Disorder in parity–time symmetric quantum walks
Peng Xue(薛鵬)
Beijing Computational Science Research Center,Beijing 100084,China
Keywords: parity-time symmetry,quantum walks,disorder
1. Introduction
One of the fundamental features of quantum mechanics is associated with the Hermiticity of Hamiltonian operators,which implies both real eigenenegies and conserved probabilities. Recently, more and more attention is attracted by a wide class of non-Hermitian Hamiltonians with party-time(PT) symmetry,[1]which still show entirely real spectra. PTsymmetric dynamics have been implemented in various physical systems,[2-14]where PT-related notions and behaviors can be observed and experimentally investigated.[15-22]However,the effect of disorder in a non-Hermitian system is still less investigated.
It is well known that static disorder leads to an absence of diffusion and the wavefunction of the particle becomes localized, which was first predicted by Anderson in 1958.[23]The so-called Anderson localization has been investigated in various physical systems,for example,photons in semiconductor powders,[24]light in photonic lattices,[25,26]and light or photons in quantum-walk architectures,[27-30]or even via Bose-Einstein condensates.[31,32]However,no effect of disorder has even been observed in a non-Hermitian system.
Quantum walks provide a good testbed for quantum computations,[33]quantum communications,[34,35]quantum measurements,[36]and quantum simulations.[18,37-40]In this paper, we present the experimental realization of PTsymmetric quantum walks for single photons[41-47]with controlled dynamics,in which controllable coin operations allow us to simulate different environmental influences including static disorder and dynamic disorder.

2. Theoretical model
Firstly, we define a split-step unitary quantum walk described by the operator

whereεis complex,in general,andε0is a negative real number. However, whenUgl(= e-ε0Ull)possesses PT symmetry and the eigenstate|ψλ〉is the eigenstate of the PT symmetry operator,εis guaranteed to be real. Here we derive the eigenvalue of the PT-symmetric non-unitary quantum walks in the homogeneous system,and derive the condition that the quasieigenenergyεbecomes real.
To this end, by assuming that angles of coin operatorsθ1andθ2are constants over the position space, we describe the non-unitary time-evolution operatorUglin the momentum space. With the Fourier transformation, the coin, conditional position shift, and gain-loss operators are rewritten respectively as

Since the presence of PT symmetry guarantees|λgl|=1,we find that the value ofd0(k) determines that the system is in the unbroken PT-symmetric phase (|d0(k)|< 1 for allk ∈[0,2π)), the broken PT-symmetric phase (|d0(k)|>1, at least,for somek),or at the exceptional point(|d0(k*)|=1 for somek*and|d0(k)|<1 for otherk).
Therefore, by recovering the prefactor of the right hand side of Eq.(9),the real and imaginary parts of the eigenvalueλof the non-unitary quantum walks with alternating losses,Ull,is described as follows:

We show the presence or absence of complex quasieigenenergies in Fig. 1. When the PT symmetry is unbroken, all quasi-eigenenergies are all real and are plotted in the light blue squares.Whereas,when the PT symmetry is broken,quasi-eigenenergies are complex and shown in the light red areas. The size of the light red area is due to the loss parameter.Here we choosel1=1 andl2=0.8. The colored dots denote the parameters we choose for experiments.

Fig. 1. Presence or absence of complex quasi-eigenenergies. When PT symmetry is unbroken, all quasi-eigenenergies are all real and are plotted in the light blue squares. Whereas, when PT symmetry is broken, quasieigenenergies are complex and shown in the light red areas. The size of the light red area is due to the loss parameter. Here we choose L1 =1 and L2=0.8.The colored dots denote the parameters we choose for experiments of quantum walk in the unbroken PT-symmetric phase ({θ1 =π/3,θ2 =0.23π},red dot),at the exceptional point({θ1=π/3,θ2=0.2754π},black dot),and in the broken PT-symmetric phase({θ1=π/3,θ2=0.32π},blue dot),respectively.
3. Experimental realization


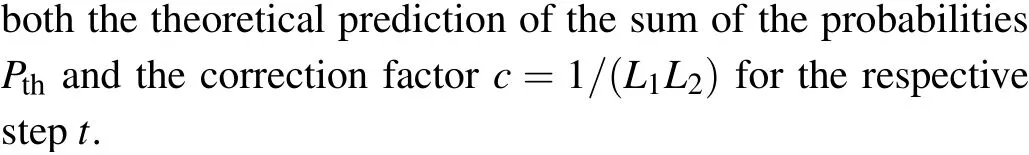


Fig.2.Experimental setup.Photons in pair are generated via the SPDC in PPKTP,with one serving as a trigger photon and the other as the quantum walker projected into the quantum-walk network. The coin operation C is implemented by a HWP and the shift operator S is implemented via a BD. The loss operator L is implemented via a PPBS.Photons appearing in the spatial modes at the output of the quantum-walk network are detected by single photon detectors(as known as APDs),in coincidence with the trigger photon.
4. Experimental results
We experimentally analyse the PT-symmetric quantum walk with various coin angles (θ1,θ2) = (π/3,0.23π),(θ1,θ2) = (π/3,0.2754π), and (θ1,θ2) = (π/3,0.32π), respectively,and with fixed loss parameters(L1,L2)=(1,0.8)as illustrated in Fig.1.For the fist case with the choice of the coin parameters (θ1,θ2) = (π/3,0.23π), the quasi-eigenenergies of the walker+coin system remain entirely real and the corresponding non-unitary time evolution preserves PT symmetry. For the second case of the choice of the coin parameters(θ1,θ2)=(π/3,0.2754π),the PT-symmetric quantum walk is now at the exceptional point from the unbroken to broken PTsymmetric phase. For the third case,by further increasing the coin parameterθ2to 0.32πand keepingθ1unchanged, the walker+coin system enters the broken PT-symmetric phase,in which the quasi-eigenenergies of the system are typically complex. The corrected probability distribution of the PTsymmetric quantum walk up to 6 steps and the variance of the distribution are shown in Fig.3. We can see that the experimental results represented by symbols agree well with those obtained by numerical simulations represented by curves. We can also see that for the PT unbroken case,the corrected probability distribution is almost the same as that of the standard unitary quantum walk.
For the second case, at the exceptional point, the corrected probability distribution is different from that of the standard unitary quantum walk as the peaks are squeezed a bit.However, by comparing the variances of the distributions for the two cases,we confirm that even at the exception point,the behavior of the walker is still ballistic.
However,for the PT broken case,the corrected probability distribution and the variance become completely different from the standard unitary quantum walk. The distribution is now Gaussian-like,which is a typical phenomenon in the broken PT-symmetric phase. The variance also confirms that the walk shows a diffusive behavior.



Fig.3. Experimental results of the PT-symmetric quantum walk with the coin angles(θ1,θ2)=(π/3,0.23π),(θ1,θ2)=(π/3,0.2754π),and(θ1,θ2)=(π/3,0.32π),respectively,and with loss parameters(L1,L2)=(1,0.8). Variances for the quantum walk up to 50 in(a)and 6 steps in(b)vs. the number of the steps. Colored curves indicate the numerical simulations of the variances, while experimental results are presented by symbols. Experimental errors are due to photon counting statistics. (c)-(e) Experimental results of the probability distributions for all the three cases of PT unbroken, PT broken,and exception point,respectively.

Fig. 4. Experimental results of the disordered PT-symmetric quantum walk with the coin angles (θ1,θ2)=(π/3,0.23π) and with loss parameters(L1,L2)=(1,0.8). The walker+coin system is in the PT unbroken phase. Variances for the quantum walk up to 50 in (a) and 6 steps in (b) vs.the number of the steps. Colored curves indicate the numerical simulations of the variances, while experimental results are presented by symbols.Experimental errors are due to photon counting statistics. (c)-(e) Experimental results of the probability distributions of the PT-symmetric quantum walk in the PT unbroken phase without disorder,with dynamic disorder,and with static disorder,respectively.

Fig. 5. Experimental results of the disordered PT-symmetric quantum walk with the coin angles (θ1,θ2)=(π/3,0.2754π) and with loss parameters(L1,L2)=(1,0.8). The walker+coin system is at the exceptional point. Variances for the quantum walk up to 50 in(a)and 6 steps in(b)vs. the number of the steps. Colored curves indicate the numerical simulations of the variances, while experimental results are presented by symbols. Experimental errors are due to photon counting statistics. (c)-(e) Experimental results of the probability distributions of the PT-symmetric quantum walk at the exception point without disorder,with dynamic disorder,and with static disorder,respectively.

Fig. 6. Experimental results of the disordered PT-symmetric quantum walk with the coin angles (θ1,θ2)=(π/3,0.32π) and with loss parameters(L1,L2)=(1,0.8). The walker+coin system is in the PT broken phase. (a), (b) Variances vs. the number of the steps. Colored curves indicate the numerical simulations of the variances and the experimental results are presented by symbols. Experimental errors are due to photon counting statistics.(c)-(e)Experimental results of the probability distributions of the PT-symmetric quantum walk in the PT broken phase without disorder,with dynamic disorder,and with static disorder,respectively.
On the other hand, the influence of static disorder stops the spread of the walker and leads to a localization for all the three cases. The localization is further confirmed by smaller variances for all the three cases. Our experimental investigations show how the two kinds of disorders influence the behavior of the quantum walker in the PT-symmetric quantum dynamics.
5. Conclusion
We experimentally investigate how dynamic disorder and static disorder can influence the non-unitary evolution of a PT-symmetric quantum walk and show the controlled transition between the different regimes. We realize a passive PTsymmetric quantum dynamics of single photons via temporally alternating photon losses in the cascaded interferometric network. Furthermore,via controllable coin operations we simulate different environmental influences of both dynamic and static disorders on the walker+coin system,which result in a standard ballistic spread, a classical diffusive behavior, and a localization of the walker in a PT-symmetric quantum walk architecture, respectively. Our setup of the single-photon implementation of PT-symmetric quantum walks with high flexibility and full control allows us not only to study the interesting features in non-Hermitian quantum dynamics but also to simulate interesting scenarios for the community of condensed matter physics and high-energy physics. Our experimental results suggest exciting methods for the investigation of Anderson localization of non-Hermitian systems using onedimensional discrete-time quantum walks.
Acknowledgment
This work was supported by the National Natural Science Foundation of China(Grant Nos.12025401 and U1930402).
- Chinese Physics B的其它文章
- Role of compositional changes on thermal,magnetic,and mechanical properties of Fe–P–C-based amorphous alloys
- Substrate tuned reconstructed polymerization of naphthalocyanine on Ag(110)
- Anti-PT-symmetric Kerr gyroscope
- Information flow between stock markets:A Koopman decomposition approach
- Cascading failures of overload behaviors using a new coupled network model between edges
- High efficiency ETM-free perovskite cell composed of CuSCN and increasing gradient CH3NH3PbI3

