坐標觀測值的《誤差理論與測量平差基礎》教學內容設計

劉志平 李洪娜 汪林根 仇春平

(1. 中國礦業大學 江蘇省環境資源信息工程重點實驗室, 江蘇 徐州 221116; 2. 中國礦業大學 環境與測繪學院, 江蘇 徐州 221116)

0 引言

《誤差理論與測量平差基礎》(簡稱《經典平差》)是測繪工程專業核心課程之一,在該專業本科教學體系中占有非常重要的地位,也為后續研究生階段的學習提供先修基礎[1-3]。由此,《經典平差》課程教改研究一直受眾多同行關注,其中部分研究成果專注于教學模式、方法與形式革新[4-6]。然而,若按一流本科課程(“金課”)建設標準,則亟須關注《經典平差》教學內容本身的創新研究[7]。也正因此,許多學者圍繞測量平差中矩陣算子作用[7]、多余觀測值剖析[8]、測量平差模型的完善[9-11]、虛擬觀測值的理解[12]、多維觀測值的平差方法[13-14]等進行了有益的教學內容改革嘗試。當前,本專業在不斷吸收測繪新理論、新技術以適應新時代發展和專業課程教學學時不斷壓縮的雙重背景下,《經典平差》課程的重視程度在本專業相對下降[7],正成為該課程教學在將來面臨的主要挑戰,即“存量更新、增量補充”問題。

作者認為導致這種狀況的主要原因在于《經典平差》課程教學案例陳舊、類型單一、可遷移性弱,同時在處理與后續專業課程關系時易陷入首鼠兩端。例如,水準網、三角網和導線平差(對應高差、角度和邊長一維觀測值)等至今仍然是主要教學案例,然而大量照搬《大地測量學基礎》《攝影測量原理》《GNSS測量原理》《工程測量學》《GIS原理》等核心專業課程中的測量平差問題又會產生重復教學矛盾。鑒于此,本文立足于測繪類專業的高精度、高可靠位置服務這一本質,牢牢抓住“坐標觀測值”的測量平差問題作為測繪類核心專業課程的有機聯系,試圖圍繞點、線、面構建二維平面、三維空間中的多種坐標觀測值方程,既豐富了《經典平差》教學案例的內容類型、增強了可遷移性,又避免了與后續核心專業課程的重復教學矛盾。與此同時,深入探討了坐標觀測值平差模型屬性特點,揭示了現有教材中關于多余觀測數計算存在的不足,為《經典平差》教學內容革新提供了新思考。

1 二維平面的坐標觀測值方程

1.1 橢圓方程

在高斯平面坐標系中,設橢圓上的坐標觀測值為(x,y),橢圓圓心坐標參數為(x0,y0),旋轉角參數θ,二維半軸參數為(rx,ry),則可寫出坐標觀測值表示的二維平面橢圓方程

(1)

進一步,對式(1)進行整理化簡可得橢圓的二元二次方程

Ax2+By2+Cxy+Dx+Ey+F=0

(2)

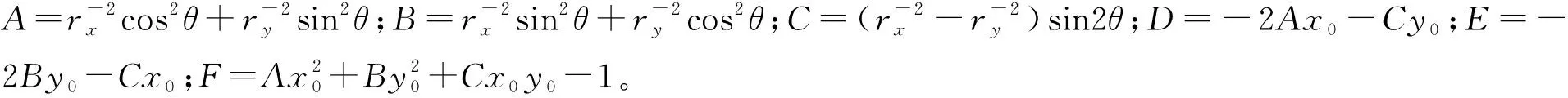
特殊地,當θ=0,rx=ry=r,則式(2)退化為二維平面的圓方程

x2+y2+D′x+E′y+F′=0

(3)

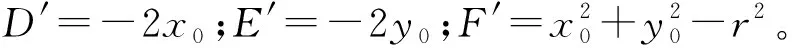
分析式(1)可知,確定平面橢圓位置、大小、形狀的必要參數為5個。式(2)中含6個參數,表明參數之間相關且有1個非必要參數。一般可采用A=1,B=1或者A2+B2=1等的限制條件。分析式(3)可知,確定平面圓位置、大小的必要參數個數為3,與式(3)的參數個數相同,表明參數之間不相關。此外,當有N個坐標點,則坐標觀測值個數為2N,一般條件方程個數為N。

1.2 共線方程

(4)

分析式(4)可知,若有N個二維坐標點滿足同一共線條件,則坐標觀測值個數為2N,一般條件方程個數為N-2。進一步分析可知,式(4)本質上為平面坐標共線的條件平差方法。若利用間接平差方法,平面直線擬合僅需要2個必要參數。

1.3 方位方程

設xi=(xi,yi),xj=(xj,yj)分別為高斯平面坐標系下的兩個點坐標,當已知它們與某中心站點x0的已知夾角為αij,則可列立坐標觀測值表示的已知夾角方程

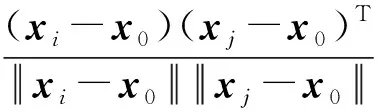
(5)

分析可知,當α=0°或α=180°,式(5)實際上表示xj、x0、xi滿足三點共線條件;當α=90°,式(5)實際上表示直線(x0,xj)與直線(x0,xi)滿足正交條件。此外,當直線(x0,xj)與坐標縱軸平行,則式(5)實際上表示(x0,xi)的坐標方位角。此時,對于已知站點x0與N個坐標點可形成N個已知方位Ai,則坐標觀測值表示的已知方位方程

(6)

分析式(6)可知,對于中心站點x0和N個坐標點xi,若已知相應的N個已知方位Ai,不考慮中心站點坐標誤差的情況下,則坐標觀測值個數為2N,一般條件方程個數為N。

1.4 平行四邊形方程

在高斯平面坐標系中,設四邊形中按逆時針編號的4個角點坐標分別為x1=(x1,y1),x2=(x2,y2),x3=(x3,y3),x4=(x4,y4),為了將該四邊形修正為平行四邊形,則需根據平行四邊形的任意一個判定條件:(1)對邊相等;(2)對角相等;(3)對邊平行條件;(4)中心對稱圖形。建立相應的坐標條件方程

(7)

(8)

(9)

x2+x4=x1+x3

(10)

式(7)～(10)分別為以距離表示的對邊相等方程、以角度余弦表示的對角相等方程、以零行列式表示的平行方程和以對角線中心重合表示的中心對稱方程。顯見,式(10)為線性方程,其余均為非線性方程,表明通過適當的參數選取方式可有效簡化方程復雜性或者降低平差模型復雜性。進一步,若需要獲得平行四邊形的中心坐標參數xc,則可重新列立包括4個角點坐標和1個中心坐標在內的一般條件方程

(11)

分析式(11)可知,對于4個角點的平行四邊形修正要求,在選取1個中心坐標作為參數的情況下,則坐標觀測值個數為8,一般條件方程個數為4。

1.5 坐標轉換

設xI=(xI,yI)T和xII=(xII,yII)T分別為兩個不同高斯平面坐標系下的某公共點二維坐標,則它們存在如式(12)的坐標轉換關系[14]

(12)

式中,k為尺度參數;θ為旋轉角參數;dx,dy表示平移參數。

分析式(12)可知,必要參數個數為4。若有N個公共坐標點,在僅假設源坐標系下坐標沒有誤差的情況下,則坐標觀測值個數為2N,一般條件方程個數為2N。

2 三維空間的坐標觀測值方程

2.1 橢球方程

將二維平面拓展到三維空間,可以參考式(2)直接寫出三維橢球的三元二次方程

(13)

特殊地,若三維半軸相等時,即rx=ry=rz=r,則三維橢球退化為三維圓球方程

x2+y2+z2+Gx+Hy+Iz+J=0

(14)

2.2 圓曲線方程

設平面上的某三維坐標記為(x0,y0,z0),該平面法向量記為(a,b,c),則可建立該平面的點法式平面方程。同時,結合三維空間的圓球方程式(14),則可以建立由平面與圓球在三維空間相交而成的三維圓曲線方程

(15)

式中,d=-ax0-by0-cz0。

分析式(15)可知,三維空間的平面式含有4個參數,圓球式含有4個參數。其中,法向量為非零向量,能夠通過某種標準化施加1個限制條件,例如a=1,b=1,c=1或者a2+b2+c2=1等。由此表明,平面式僅含3個必要參數,三維圓曲線包括7個必要參數。此外,當有N個坐標點,則坐標觀測值個數為3N,一般條件方程個數為2N。

進一步地,若式(15)中的平面穿過圓球的圓心,則需要再增加1個限制條件

a·G+b·H+c·I=2d

(16)

2.3 共面方程

[(xi+1-xi)×(xi+2-xi)](xi+3-xi)T=0

(17)

分析式(17)可知,若有N個坐標點滿足同一共面條件,則坐標觀測值個數為3N,一般條件方程個數為N-3。進一步分析可知,式(17)本質上為三維坐標共面的條件平差方法。若利用間接平差方法,三維平面擬合僅需要3個必要參數。

2.4 直線方程

根據三維空間的平面方程式原理,當兩個不同的平面在三維空間相交的交線則可以形成直線,則由坐標觀測值表示的三維直線方程如下[15]

(18)

分析式(18)可知,根據平面法向量不為零向量,則需對兩個平面施加2個限制條件,具體限制條件可以參考2.2節。具體地,式(18)中8個參數,包括6個必要參數、2個非必要參數。此外,當有N個坐標點,則坐標觀測值個數為3N,一般條件方程個數為2N。

2.5 坐標轉換

設XI=(xyz)T和XII=(XYZ)T分別為兩個不同空間直角坐標系下的某公共點三維坐標,則它們存在如式(19)的坐標轉換關系[16]:

XI=k·R·XII+T

(19)

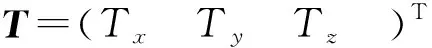
分析式(19)可知,必要參數個數為7。若有N個公共坐標點,在不考慮源坐標系下坐標誤差的情況下,則坐標觀測值個數為3N,一般條件方程個數為3N。

3 坐標觀測值平差模型屬性分析

基于第1和第2節的分析,若有N個坐標點,分別按二維橢圓方程式(2)、二維圓方程式(3)、二維共線方程式(4)、二維方位方程式(6)、平行四邊形方程式(11)、二維坐標轉換方程式(12)和三維橢球方程式(13)、三維圓球方程式(14)、三維圓曲線方程式(15)、三維共面方程式(17)、三維直線方程式(18)、三維坐標轉換方程式(19)。若將坐標觀測值個數記為n、確定模型的必要參數個數記為t、選取參數個數記為u、一般條件方程個數記為c、限制條件方程個數記為s、模型自由度記為f、多余觀測數記為r,并建立相應平差函數模型,則各平差模型的屬性數據如表1所示。

表1的建模方式表示利用坐標數據建模的方式。從表1可看出,本文討論的二維平面、三維空間的坐標觀測值平差模型較好地覆蓋了《誤差理論與測量平差基礎》的四種經典平差方法。其中,(1)二維共線、二維方位和三維共面均屬于條件平差模型,所選參數個數u=0;(2)平行四邊形屬于具有參數的條件平差,所選參數獨立且個數ut,形成s=u-t個限制條件方程。需指出的是,限制條件個數公式s=max(u-t,0)更具有普適性。此外,通過表1加強認識模型屬性數據的規律:即一般條件個數c與限制條件個數s之和等于參數個數u與多余觀測數r之和,即c+s=r+u。其中,多余觀測數r等價于平差模型自由度f,即r=f=c+s-u。同時,根據限制條件數s=max(u-t,0),可得更具普適性的多余觀測數公式r=c-min(u,t)。

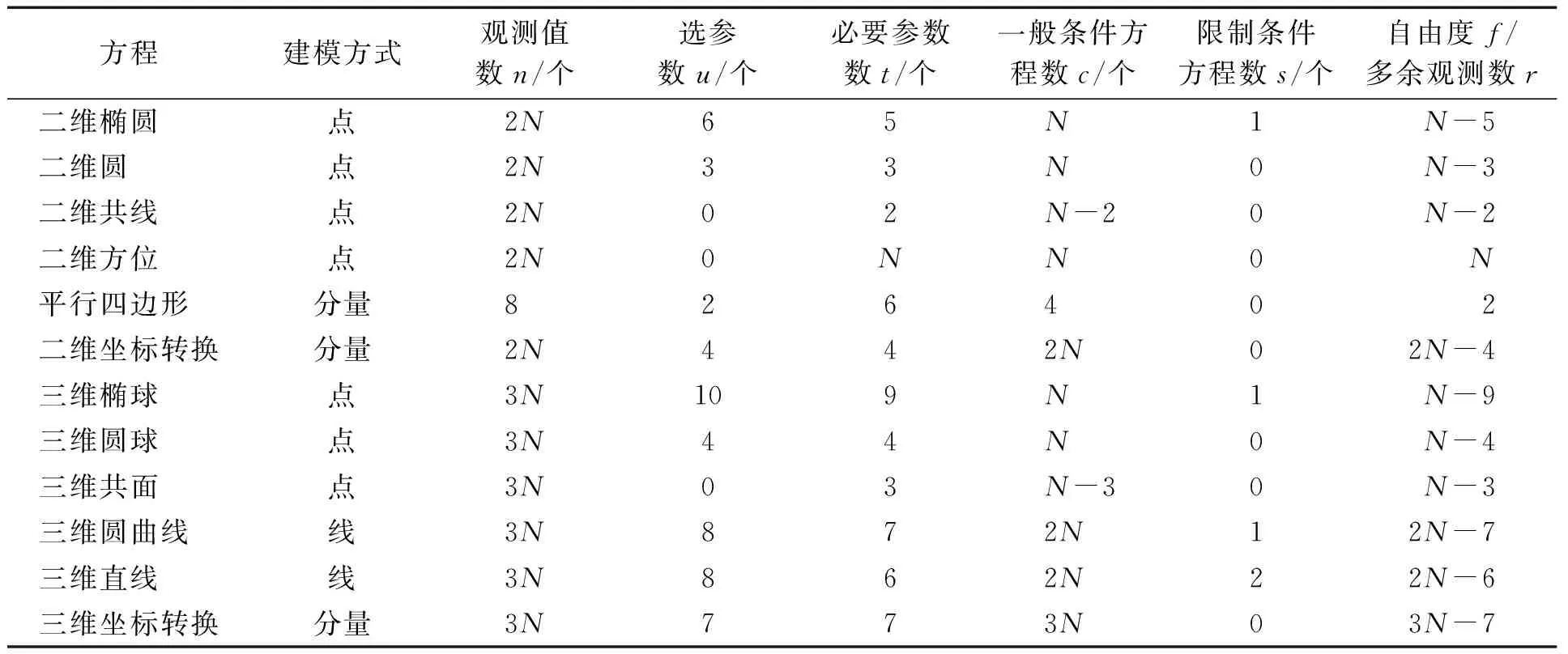
表1 N個坐標點的平差模型屬性數據

進一步分析表1中二維坐標觀測值的平差情形可得:(1)對于二維共線的條件平差模型,多余觀測數r=c-min(u,t)=N-2,然而按照現有教材的多余觀測計算式,多余觀測數r=n-t=2N-2,顯然不正確;(2)對于平行四邊形的具有參數條件平差模型,多余觀測數r=c-min(u,t)=2,與現有教材r=n-t=2結果一致;(3)對于二維坐標轉換的間接平差模型,多余觀測數r=c-min(u,t)=2N-4,即N>2,與現有教材r=n-t=2N-4結果一致;(4)對于二維橢圓的概括平差模型,多余觀測數r=c-min(u,t)=N-5,即N>5,然而按照現有教材的多余觀測計算式,則多余觀測數r=n-t=2N-5顯然不正確。由此顯見,當且僅當采用坐標分量建模方式,由于一般條件方程個數與坐標維數成正比,現有教材的多余觀測數計算式正確;而當利用非坐標分量建模方式,由于一般條件方程個數與坐標維數沒有確定性關系,導致現有教材的多余觀測計算式錯誤。因此,本文多余觀測值計算式,同時適用于坐標分量和非坐標分量建模方式。同理,該結論也適用于三維觀測值的平差模型,限于篇幅要求不再贅述。綜上,本文通過探討進一步明確了坐標觀測值平差模型中多余觀測值的內涵,建議將多余觀測值計算式改為r=c-min(u,t),其中c表示一般條件方程個數,t表示必要參數個數,u表示所選參數個數。

4 結束語

作者通過《經典平差》多年教學經驗發現,隨著專業課程專業學時減少和測繪新技術快速發展,該課程近年來面臨比較嚴峻的課程體系“存量更新、增量補充”問題。鑒于此,本文緊緊抓住測繪類專業的位置服務本質,通過構建以二維、三維坐標觀測值為研究對象的“點線面”測量平差問題,既拓廣了高差、邊長和角度一維觀測值的傳統課程案例邊界,又加強了與《大地測量學基礎》《攝影測量原理》《GNSS測量原理》《GIS原理》等后續核心專業課程的通用性聯系。與此同時,通過5類二維和5類三維坐標觀測值平差模型的屬性數據分析,指出了現有教材多余觀測數計算式存在的不足，并給出了坐標分量和非坐標分量建模方式的多余觀測數通用計算式。總之,本文依據“內容為王、通用呈現”的坐標觀測值測量平差教學內容設計思路,為持續增強學生在誤差理論方面的遷移學習能力提供借鑒。