新型變齒磁流體密封結構設計及性能研究

吳朝軍 朱維兵 顏招強 張 林 王和順

(1.西華大學機械工程學院 四川成都 610039；2.自貢兆強密封制品實業有限公司 四川自貢 643000)

20世紀60年代，磁流體密封技術被用于火箭液體燃料穩固和宇航服真空密封后逐漸進入人們的視野[1]。磁流體密封具有“零泄漏”、使用壽命長、可靠性高、低維修成本、抗干擾能力強等特點，目前廣泛應用于航天、電子、化工、機械、能源、環保、醫療等領域[2]。磁流體密封的結構設計是決定密封間隙內磁感應強度分布及密封性能的關鍵因素。因此，在設計磁流體密封結構需準確計算出密封結構內磁感應強度分布。常規數值方法很難準確計算出密封結構內磁感應強度分布，而有限元計算法為解決這一難點提供了有效的途徑。因此新型磁流體密封結構設計并利用有限元方法進行磁場分析已成為該領域的研究熱點。

2002年李德才等[3]設計了應用于干式羅茨真空泵的磁流體密封，并對密封磁場進行有限元分析。2004年李保鋒等[4]利用有限元數值計算方法及實驗證實了變齒寬結構能夠提升磁流體密封耐壓能力，但未確定具體的齒寬變化系數。2006年李國斌等[5]利用有限元方法分析對比對齒聚磁結構和單側極齒聚磁結構的聚磁性能，發現對齒結構中間極齒磁感應強度遠大于單側極齒結構，且密封性能約為單側極齒結構的2倍。2012年RADIONOV等[6]考慮極靴和轉軸材料的非線性磁性，通過有限元軟件分析了磁流體密封裝置的磁場強度分布以及磁流體的流動特性，發現磁場強度和磁流體流動特性在不同位置處存在明顯差異。2016年吳旭東等[7]在傳統高速磁流體密封裝置的基礎上對密封結構關鍵部件進行優化設計，并利用有限元軟件模擬計算出優化后磁流體密封結構中的磁感應強度，驗證了優化結構的合理性。楊小龍等[8]以階梯式迷宮密封為基礎提出了一種階梯式磁流體密封結構，并通過有限元數值計算方法分析階梯式磁流體密封結構密封間隙內磁場強度并計算出密封耐壓能力，發現隨著徑向密封間隙的增大階梯式磁流體密封耐壓性能降低。2020年PARMAR等[9]通過有限元軟件分析了不同極齒結構、密封間隙、磁流體飽和磁化強度對密封性能的影響。呂濤濤等[10]運用有限元軟件分析磁流體密封結構中磁場強度分布，得到極齒結構參數、數量及密封間隙對磁場強度的影響。

磁流體密封裝置一般是安裝在其他設備上使用，所以對尺寸和質量有一定限制，要求在有限的空間內密封裝置能滿足耐壓要求。而目前磁流體密封裝置想要提高密封耐壓值需增加密封級數[11]，這與尺寸的限制要求相沖突。針對在密封級數不變情況下而提高密封耐壓值這一問題，本文作者設計了一種新型變齒磁流體密封結構，并利用ANSYS Maxwell有限元軟件對密封間隙內磁感應強度大小進行計算，采用控制變量法分析不同變齒系數對磁流體密封性能的影響，確定密封性能最優的變齒系數，為磁流體密封裝置的設計提供一種新的思路，拓展了磁流體密封的使用范圍。

1 新型變齒磁流體密封

1.1 新型變齒磁流體密封結構設計

磁流體是一種新型的功能材料，它是將納米級的固體磁性材料通過表面活性劑均勻分散在液體介質中而形成的穩定膠體溶液[12]。圖1是磁流體組成示意圖。磁流體不但擁有流體特性而且具有磁響應特性，所以應用領域廣泛且發揮作用越來越大，在密封領域尤為突出。

圖1 磁流體組成示意

基于傳統磁流體密封結構，設計了一種新型變齒磁流體密封結構，如圖2(a)所示。其主要由永磁鐵、變齒極靴、旋轉軸、磁流體、密封外殼組成。根據轉軸軸徑為30 mm及文獻[13]設計變齒磁流體密封各元件：變齒極靴內徑Ra、外徑Rg、軸向寬度W尺寸分別為15.2、33、10 mm；永磁鐵內徑Ra、外徑Rg、軸向寬度W尺寸分別為23、33、9.5 mm；外殼內徑Ra、外徑Rg、軸向寬度W分別為33、36、37 mm。各元件尺寸參數詳情如表1所示。

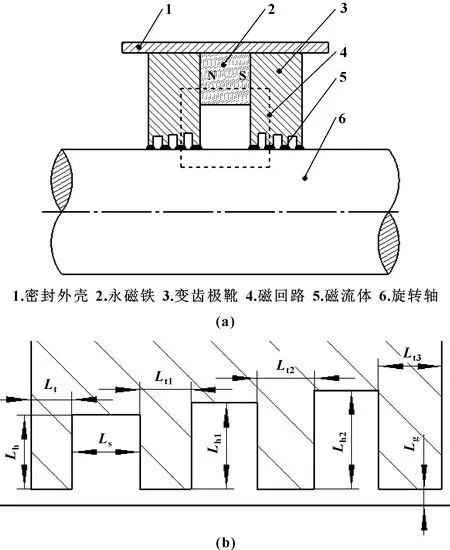
圖2 變齒磁流體密封結構示意

表1 密封元件尺寸參數

由于變齒磁流體密封結構中極齒尺寸隨變齒系數的改變而變化，所以設計一套傳統極齒結構并以該結構為基礎分析各變齒系數對密封性能的影響，確定最優變齒系數。其齒寬Lt、齒高Lh、齒槽寬Ls、密封間隙Lg、單個極靴極齒數量N分別為1、1.8、2、0.2 mm、4，尺寸參數詳情如表2所示，密封結構如圖2(b) 所示，則變齒寬系數λ和變齒高系數γ可用式(1)表示。

表2 極齒尺寸參數

(1)

1.2 新型變齒磁流體密封工作原理

由于磁回路的存在以及磁流體具有磁場響應特性，所以注入密封間隙內的磁流體會匯聚在變齒極靴與旋轉軸的密封間隙內并形成多個“O”形密封圈。磁流體“O”形密封圈在工作過程中的位置和形狀隨著密封介質側壓力的變化而改變，變化過程如圖3所示。圖3中左側為密封介質側，右側為外界。當左右兩側壓力相等磁流體“O”形密封圈不發生變化，如圖3(a)所示；當左側壓力大于右側壓力時磁流體“O”形密封圈向右移動并發生彎曲變形，如圖3(b)所示；當左側壓力大于右側壓力一定值時磁流體“O”形密封圈中會形成氣孔，如圖3(c)所示；當左右兩側壓差超過磁流體密封耐壓極限時磁流體“O”形密封圈會被擊穿導致密封失效，如圖3(d)所示。破壞后的磁流體“O”形密封圈左右兩側壓力相等，由于磁流體密封的自恢復特性則磁流體又會重新愈合，恢復耐壓能力[14]。為了提高磁流體密封耐壓值，一般將磁流體密封設計為多極齒的結構，因為磁流體密封裝置的耐壓值為各磁流體“O”形密封圈的耐壓值之和[15]。

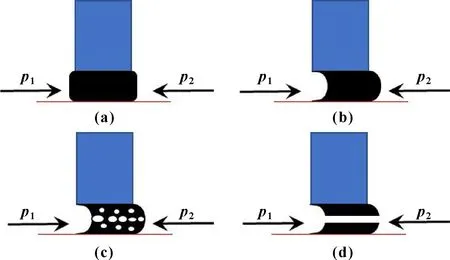
圖3 磁流體工作變形示意

1.3 新型變齒磁流體密封耐壓理論

在一般情況下，磁流體的伯努利方程[16]可表示為

(2)

式中：p為磁流體的復合壓力，Pa；ρf為磁流體密度，kg/m3；v為磁流體速度,m/s；g是重力加速度，m/s2；h為磁流體參考高度,m；μ0為真空磁導率；M為磁流體磁化強度，A/m；H為外磁場強度,T；C是常數。

對于磁流體密封中的靜壓場合，速度對磁流體密封的影響可以忽略。同樣由于密封間隙內的磁場力遠大于重力，所以密封間隙中的重力效應也可以忽略。因此，磁流體密封的總密封壓力簡化為

MsΔBsum

(3)

通過式(3)不難發現新型變齒磁流體密封耐壓性能主要取決于磁流體的飽和磁化強度以及總的磁感應強度差。所以要提高磁流體密封的耐壓能力主要從研發出具有高飽和磁化強度的磁流體和提高密封結構總磁感應強度差ΔBsum2個方面入手[17]。

2 仿真模型建立與計算

2.1 模型建立及材料選擇

由于新型變齒磁流體密封結構為軸對稱結構，所以在Maxwell軟件中將模型簡化為以Z軸為對稱軸的二維平面結構。根據前面所設計的磁流體密封結構參數進行仿真模型建立，并在模型周圍創建計算區域。仿真分析模型如圖4所示。

圖4 仿真模型

模型建立完成后對各元件進行材料選擇及添加，其中轉軸、變齒極靴材料為10鋼；永磁鐵材料為釹鐵硼(NdFe35)，其相對磁導率μr=1.099 H/m，矯頑力Hc=8.9×105A/m；密封外殼材料為鋁；計算區域定義為空氣。各元件材料詳情如表3所示。

表3 密封元件材料

2.2 仿真條件設置與計算

在計算條件設置中將永磁鐵的充磁方向設置為+Z方向且磁力線平行于Z軸，計算區域邊界AB、BC、AD設置Balloon邊界，計算最大迭代步數設置為30，誤差設置為1%。網格劃分采用軟件默認的四面體網格，每次迭代網格加密設置為30%，非線性殘差設置為0.1%。圖5所示為模型密封間隙周圍網格劃分。設置完成后便可進行檢驗計算。

圖5 網格劃分

3 仿真結果與性能分析

3.1 仿真結果

圖6所示為計算完成后計算區域的磁場強度分布。可知，磁場強度分布存在明顯差異，在極齒與旋轉軸之間的密封間隙處磁場強度最大，其余區域較小且均勻。根據磁流體具有磁場響應特性，磁流體會聚集在密封間隙中磁場強度大的區域，并形成磁液密封圈起到密封作用。

圖6 磁場強度分布

為了查看極齒和旋轉軸密封間隙的磁感應強度變化，通過軟件后處理器在密封間隙中間位置定義一條平行于Z軸的軌線E-F，如圖7所示。通過將計算出的磁感應強度映射到此軌線上進行分析討論。

圖7 磁感應強度測量位置

3.2 變齒寬系數對密封性能的影響

當密封間隙為0.2 mm時，沿軌線E-F方向不同變齒寬系數下密封間隙內磁感應強度及變化曲線如圖8所示，其中變齒寬系數λ分別為1、1.1、1.2、1.3、1.4。可知，磁感應強度映射到軌線E-F上時呈現出結構性變化規律，波峰對應極齒位置磁感應強度，波谷對應齒槽位置磁感應強度。傳統磁流體密封結構即變齒寬系數λ=1時，由于邊緣效應的存在所以中間2個極齒位置對應的磁感應強度更大，左右兩極齒位置對應磁感應強度被削弱了。而新型變齒寬磁流體密封結構中極齒寬度沿軌線E-F方向逐漸增加，右邊極齒邊緣效應的影響減小，所以沿軌線E-F方向極齒、齒槽位置對應磁感應強度逐漸增大。隨著變齒寬系數的增加，遠離永磁體位置的2個極齒位置對應的磁感應強度逐漸減小，而靠近永磁體位置的2個極齒位置對應的磁感應強度逐漸增大后再減小。

圖8 不同變齒寬結構磁感應強度分布

根據上述計算結果計算各λ系數下磁感應強度差ΔBsum的大小，結果如圖9所示。可知，隨著變齒寬系數的增加磁感應強度差ΔBsum先增加后減小，并且在λ=1.2時值最大。根據公式(3)說明新型變齒寬結構可以提高磁流體密封的耐壓能力。以上分析結果與文獻[4]通過實驗得到的變齒寬結構能提高密封承壓值的結論是一致的，說明文中仿真計算方法及參數設置是正確的。

圖9 磁感應強度差與變齒寬系數的關系

3.3 變齒高系數對密封性能的影響

在密封間隙為0.2 mm時，沿軌線E-F方向不同變齒高系數下密封間隙內磁感應強度及變化曲線如圖10所示，其中變齒高系數γ分別為1、1.1、1.15、1.2、1.25。可知，與傳統磁流體密封結構即變齒高系數γ=1時相比較，新型變齒高磁流體密封結構中極齒高度沿軌線E-F方向逐漸增加，右邊兩極齒、齒槽對應的磁感應強度受邊緣效應的影響更加明顯，所以沿軌線E-F方向右邊兩極齒位置對應磁感應強度被削弱減小。隨著變齒高系數的增加，在遠離永磁體位置的兩極齒、齒槽處的磁感應強度大小受變齒高系數影響很小，但靠近永磁體位置的兩極齒、齒槽處的磁感應強度隨著變齒高系數的增加逐漸減小。

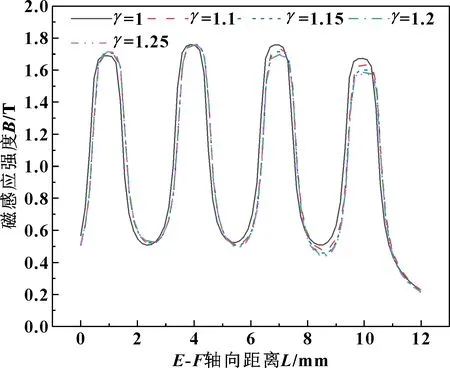
圖10 不同變齒高結構磁感應強度分布

根據上述計算結果計算各γ系數下磁感應強度差ΔBsum的大小，結果如圖11所示。可知，隨著變齒高系數的增加磁感應強度差ΔBsum逐漸減小，說明變齒高結構會降低磁流體密封的耐壓能力。

圖11 磁感應強度差與變齒高系數的關系

3.4 混合變齒系數對密封性能的影響

在密封間隙為0.2 mm時，沿軌線E-F方向分析不同變齒寬系數及變齒高系數共同對密封間隙內磁感應強度大小分布的影響，進而得到對密封性能的影響，其中變齒寬系數λ、變齒高系數γ取值同前面一致。

首先，分析一系列變齒寬結構下不同變齒高系數對磁感應強度差ΔBsum大小的影響，其結果如圖12所示。可知，隨著變齒高系數的增加不同變齒寬結構對應的磁感應強度差值呈現不同的變化趨勢。其中變齒寬系數為1.1、1.2的變齒寬結構對應的磁感應強度差值明顯大于其余結構，并在變齒寬系數、變齒高系數均為1.1時磁感應強度差值最大。變齒寬系數為1.3的變齒寬結構隨變齒高系數的增加磁感應強度差值變化情況和傳統結構相反。變齒寬系數為1.4的變齒寬結構隨著變齒高系數的增加磁感應強度差值變化略有波動，但其磁感應強度差值明顯低于其他變齒結構的磁感應強度差值。

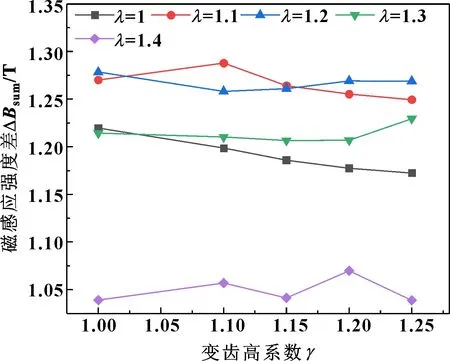
圖12 不同變齒寬結構的ΔBsum與γ的關系曲線

其次，分析不同變齒高結構情況下不同變齒寬系數對磁感應強度差值ΔBsum大小的影響，其結果如圖13所示。可知，在所有變齒高結構中隨著變齒寬系數的增加其磁感應強度差值變化趨勢相同，都是先增加后減小。其中變齒高系數為1.1、1.15的變齒高結構中磁感應強度差最大值出現在變齒寬系數為1.1的情況下，變齒高系數為1.2、1.25的變齒高結構在變齒寬系數為1.2時達到最大值。

圖13 變齒高結構ΔBsum與λ的關系曲線

4 結論

(1)以傳統磁流體密封為基礎設計了一種新型變齒磁流體密封結構，為磁流體密封裝置的設計提供了一種新的思路。

(2)通過軟件后處理器，得到了磁場強度分布云圖以及極靴和旋轉軸密封間隙中間位置磁感應強度變化曲線圖。研究發現新型變齒磁流體密封結構在極齒位置磁場強度值最大，決定了新型變齒磁流體密封的可行性。

(3)新型變齒寬密封結構中，隨著變齒寬系數的增加，磁感應強度差值先增加后減小，且在變齒寬系數為1.2時磁感應強度差值最大。因此新型變齒寬結構可以提高磁流體密封耐壓能力。

(4)新型變齒高密封結構中，隨著變齒高系數的增加，磁感應強度差值逐漸減小。因此新型變齒高結構會降低磁流體密封耐壓能力。

(5)新型混合變齒結構中，在變齒寬系數、變齒高系數均為1.1的情況下磁感應強度差值為最大值，密封性能最優。