基于GRU和XGBoost的礦壓顯現規律預測

柴敬， 劉義龍， 王安義， 屈世甲， 歐陽一博

(1.西安科技大學 能源學院， 陜西 西安 710054； 2.西安科技大學 西部礦井開采及災害防治教育部 重點實驗室， 陜西 西安 710054； 3.西安科技大學 通信與信息工程學院, 陜西 西安 710054； 4.天地(常州)自動化股份有限公司， 江蘇 常州 213015)

0 引言

煤炭開采過程破壞了巖層間原始的應力平衡狀態，在重力影響下，巖體會產生新的應力場，通常稱為礦壓顯現。劇烈的礦壓會誘發巷道變形失穩、瓦斯突出、沖擊地壓等地質災害，為煤礦生產帶來巨大的損失[1-2]。因此，為減少地質災害的發生，掌握礦壓顯現的規律并對礦壓進行有效預測和控制是煤礦安全生產的重要課題之一。

近年來，分布式光纖傳感技術[3-5]的興起有效解決了礦壓難以監測的問題。但是，由于采動過程中巖層變形具有隨機性、非線性的特點，導致礦壓規律難以預測。為解決該問題，許多學者采用光纖傳感器監測的光纖頻移值對礦壓顯現規律進行表征。王潤沛[6]基于光纖平均頻移變化度表征礦壓的原理，結合機器學習算法對礦壓進行預測。鞏師鑫等[7]基于液壓支架工作阻力數據表征礦壓的原理，采用MRDA FLPEM(流形正則域適應函數鏈接預測誤差)集成算法預測了綜采工作面礦壓。趙毅鑫等[8]利用液壓支架阻力數據分析了大采高工作面的礦壓顯現規律并采用深度學習算法預測了礦壓。常峰[9]基于工作面頂板礦壓數據，采用遺傳算法優化后的BP神經網絡模型預測了綜采工作面頂板的來壓規律。李澤萌[10]采用LSTM(Long Short-Term Memory，長短期記憶網絡)模型對支架阻力數據表征的礦壓進行預測。趙銘生等[11]基于工作面綜采條件下的礦壓破壞深度實測數據，采用遺傳算法優化后的BP神經網絡模型對礦壓破壞深度進行預測。上述研究在數據完整情況下對礦壓顯現規律進行了有效預測，但礦井環境惡劣，傳感器采集的數據存在缺失現象，導致無法準確預測礦壓顯現規律。因此，本文以義馬煤業(集團)有限責任公司千秋煤礦為工程背景，搭建三維相似物理模型，在假設光纖下半部分數據丟失的前提下，引入GRU(Gated Recurrent Unit，門控循環單元)和LSTM預測模型，對缺失的光纖頻移值進行對比預測，使用預測效果較優的缺失值填補光纖頻移值數據缺失位置。將填補后的光纖頻移值數據轉換為能表征礦壓規律的光纖平均頻移變化度數據，引入極端梯度提升(eXtreme Gradient Boosting，XGBoost)[12]模型和BP神經網絡模型進行對比預測，得到較適合的礦壓預測模型。

1 相似物理模型及光纖數據監測系統搭建

1.1 相似物理模型搭建

根據千秋煤礦的地質特征及構造(表1)搭建三維相似物理模型，如圖1所示。模型幾何相似比為1∶400，容重相似比為1∶1.6，尺寸為3 600 mm×2 000 mm×2 000 mm(長×寬×高)。模型中上覆巖層厚度為174 mm，模擬煤層厚度為60 mm，底板厚度為200 mm。在模型上方均勻放置載荷共計3.4 kPa的沙袋。自開切眼位置從左至右進行掘進，工作面推進步距為40 mm，推進總長為2 400 mm。

1.2 光纖數據監測系統搭建

在相似物理模型中埋設分布式光纖傳感器，建立光纖數據監測系統，如圖2所示。該系統由光纖傳感器、NBX-6055應力分析儀及計算機組成。在模型中部等間距布設3條垂直光纖Fv1，Fv2，Fv3，光纖數據采樣間隔為10 mm，有效長度為1 740 mm。在模擬工作面掘進時，光纖受到巖層內部變形力的作用發生頻移，通過NBX-6055應力分析儀將光信號轉換為電信號后，傳輸到計算機，最后使用計算機軟件實現對光纖數據的解析和存儲，采集到的數據以.bat格式存放。為了便于處理，將數據遷移至excel表格中，數據結構為174×60的矩陣形式，行代表整條光纖各個位置的數據，列代表工作面的推進距離。

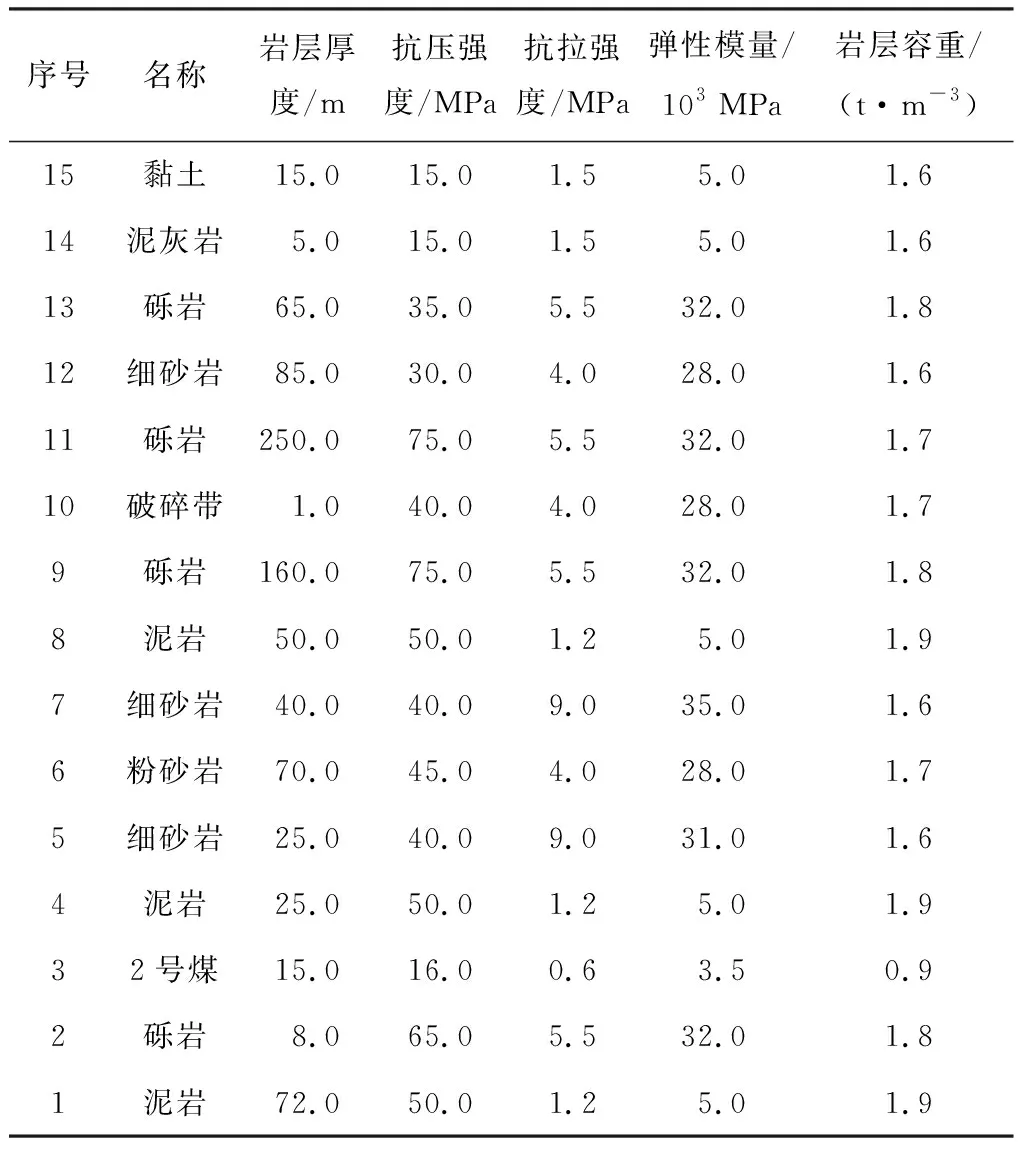
表1 覆巖結構及物理力學參數Table 1 Rock structure and physical and mechanical parameters

圖1 三維相似物理模型Fig.1 3D similar physical model

2 相關原理

2.1 光纖頻移數據表征礦壓原理

根據光纖傳感原理可知，在消除溫度因素影響后，布里淵頻移值與應變存在線性關系。布里淵頻移值的變化是傳感光纖對巖體變形破裂過程中信息變化的反映。巖層產生的變形越明顯，光纖所受應力越大，光纖監測系統測得的布里淵頻移值變化也越大；當巖層產生的變形不明顯時，光纖監測系統測得的布里淵頻移值變化小。基于上述巖層變形引起的光纖頻移值變化規律，文獻[13-16]提出了一種利用光纖平均頻移變化度表征礦壓的方法，即將光纖平均頻移變化度曲線中的“尖峰”位置作為上覆巖層礦壓顯現的判斷指標。光纖平均頻移變化度公式為

(1)

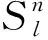
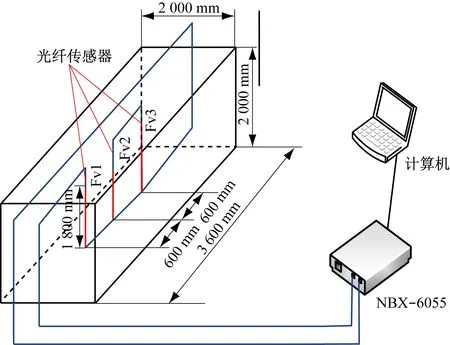
圖2 光纖監測系統Fig.2 Optical fiber monitoring system

2.2 GRU預測原理

GRU模型是基于RNN(Recurrent Neural Network，循環神經網絡)預測模型和LSTM預測模型的改進模型，既解決了RNN模型中由于共享系數矩陣導致的梯度彌散和梯度爆炸的問題，也解決了LSTM中內部單元結構冗余的問題。這使得GRU模型在運算速度上優于LSTM模型，且對小樣本數據集的預測精度更高。

GRU模型內部單元主要由重置門和更新門組成，如圖3所示。重置門可以令當前神經元的隱藏狀態遺忘與預測不相關的信息。更新門用于更新當前時刻該神經單元記憶有效信息的程度，更新門的值越大說明記憶的有效信息越多。

GRU模型內部各部分運算表達式為

r=σ(Wrxt+Brht-1)

(2)

z=σ(Wzxt+Bzht-1)

(3)

g=tanh(Wgxt+Bgrht-1)

(4)

ht=(1-z)ht-1+zg

(5)

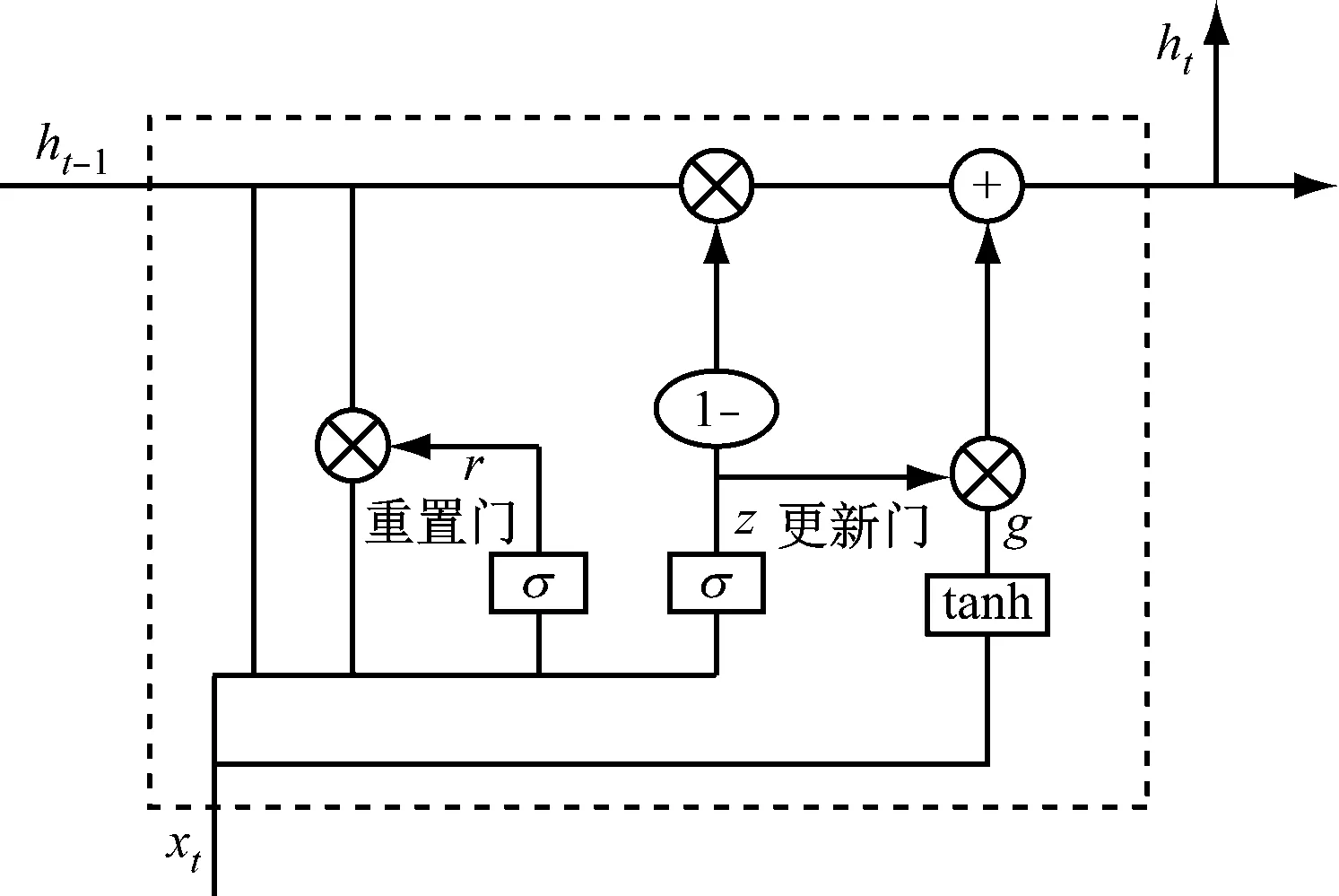
圖3 GRU網絡結構Fig.3 GRU network topology

式中：r為重置門；σ為sigmoid激活函數，表示神經元的激活率；Wr，Br，Wz，Bz，Wg，Bg分別為重置門、更新門和候選隱藏狀態的上一時刻輸出及當前時刻輸入所對應的權重矩陣；xt為t時刻的輸入；ht-1為t-1時刻的輸出；z為更新門；g為候選隱藏狀態；ht為t時刻的輸出。

2.3 XGBoost預測原理

XGBoost是在上一次模型預測的基礎上加入一顆新樹，然后去擬合前面樹的預測結果與真實值之間的殘差從而形成新模型，并將新模型作為下次模型學習的基礎，以此提升模型的預測精度。其函數為

(6)

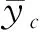
XGBoost使用的目標函數為

(7)

(8)

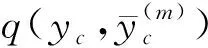
2.4 評估指標

采用平均絕對誤差MR和平均相對誤差MA作為模型預測效果的評價指標。

(9)

(10)

式中C為參與評估的樣本數。

3 基于GRU模型的缺失值處理

3.1 參數設置

為選取較優模型進行缺失值處理，對LSTM和GRU模型的預測效果進行對比。采用掘進至2 320 mm的光纖頻移值數據作為GRU和LSTM模型的數據集，將數據集按照7∶3的比例劃分為訓練集和測試集。設預測步長為1，將均方誤差函數作為損失函數，批尺寸為3，迭代次數為20。

3.2 實驗結果分析

LSTM和GRU模型的損失函數分別如圖4、圖5所示。可看出在迭代過程中，LSTM模型在7次迭代后收斂過程平穩，GRU模型在5次迭代后收斂過程平穩，訓練集損失函數和測試集損失函數均達到平穩狀態，說明GRU模型的收斂速度比LSTM模型的收斂速度快。

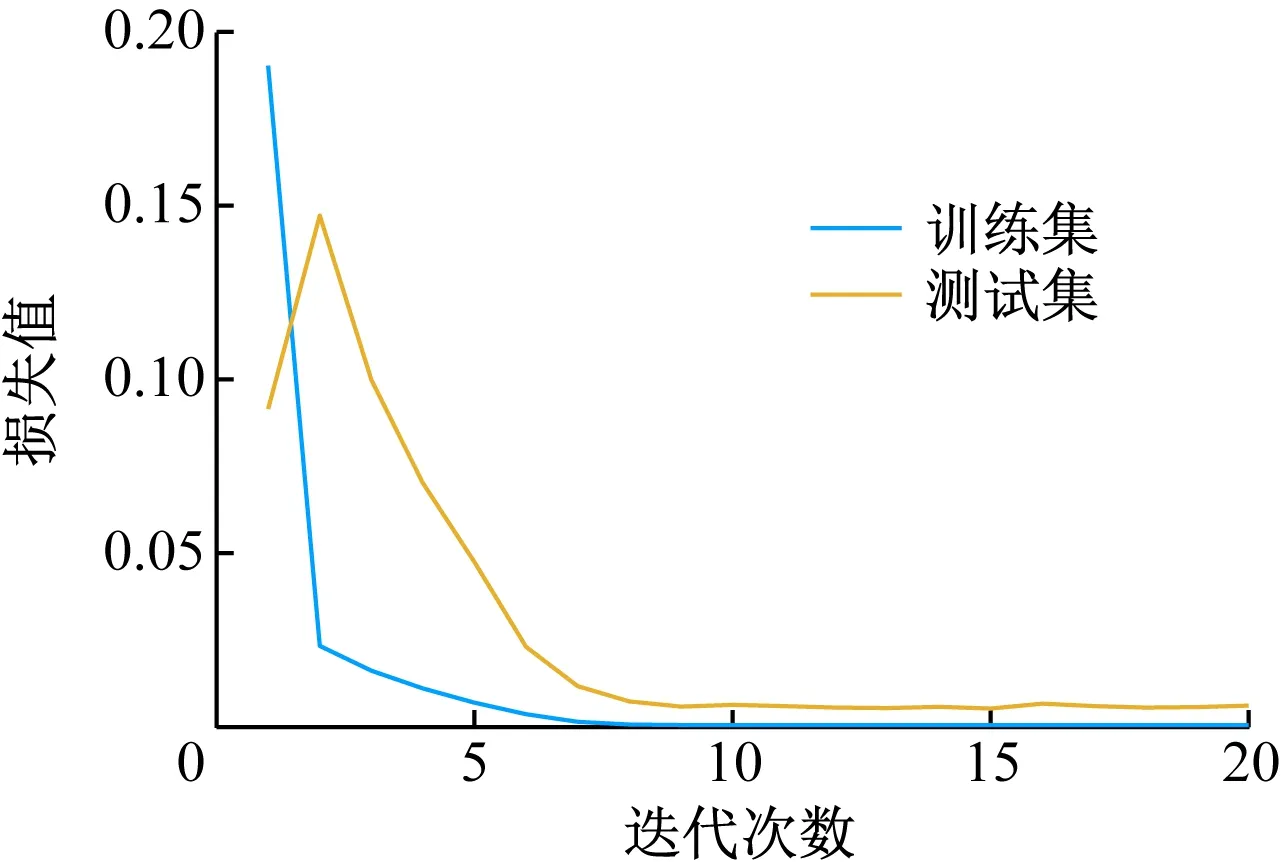
圖4 LSTM模型損失函數Fig.4 LSTM model loss function

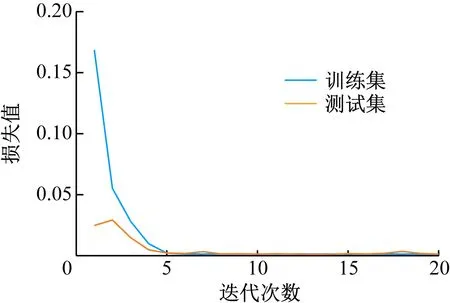
圖5 GRU模型損失函數Fig.5 GRU model loss function

LSTM和GRU模型對Fv1光纖下半部分數據反歸一化后的預測結果如圖6所示。可看出2種預測模型都能準確預測出光纖下半部分頻移數據。為衡量模型的表現能力，計算真實值和預測值的誤差可得：LSTM模型的平均相對誤差為15.63%，平均絕對誤差為17.43 MHz，GRU模型的平均相對誤差為10.84%，平均絕對誤差為9.78 MHz。說明GRU模型的精度比LSTM模型的精度高。因此，使用GRU模型對缺失值進行回歸預測可得到更優效果。

3.3 GRU模型泛化能力評估

為了評估GRU模型的泛化能力，假設工作面掘進至1 320 mm時出現缺失現象，導致在后續監測過程中，光纖監測的下半部分光纖頻移值數據均缺失，采用GRU模型進行多次預測，將預測結果填補至缺失位置，如圖7所示。與光纖原始頻移數據(圖8)對比可知，使用GRU模型預測的光纖數據與原始光纖頻移數據曲線基本一致，說明GRU模型具有良好的泛化能力。

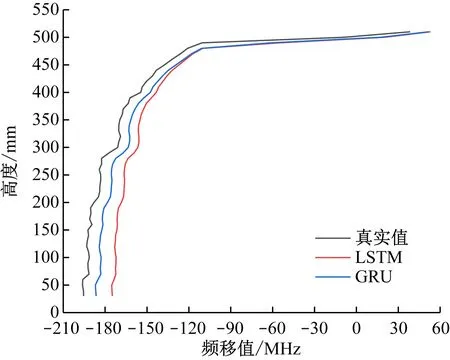
圖6 LSTM和GRU模型的預測結果Fig.6 The prediction results of LSTM and GRU models

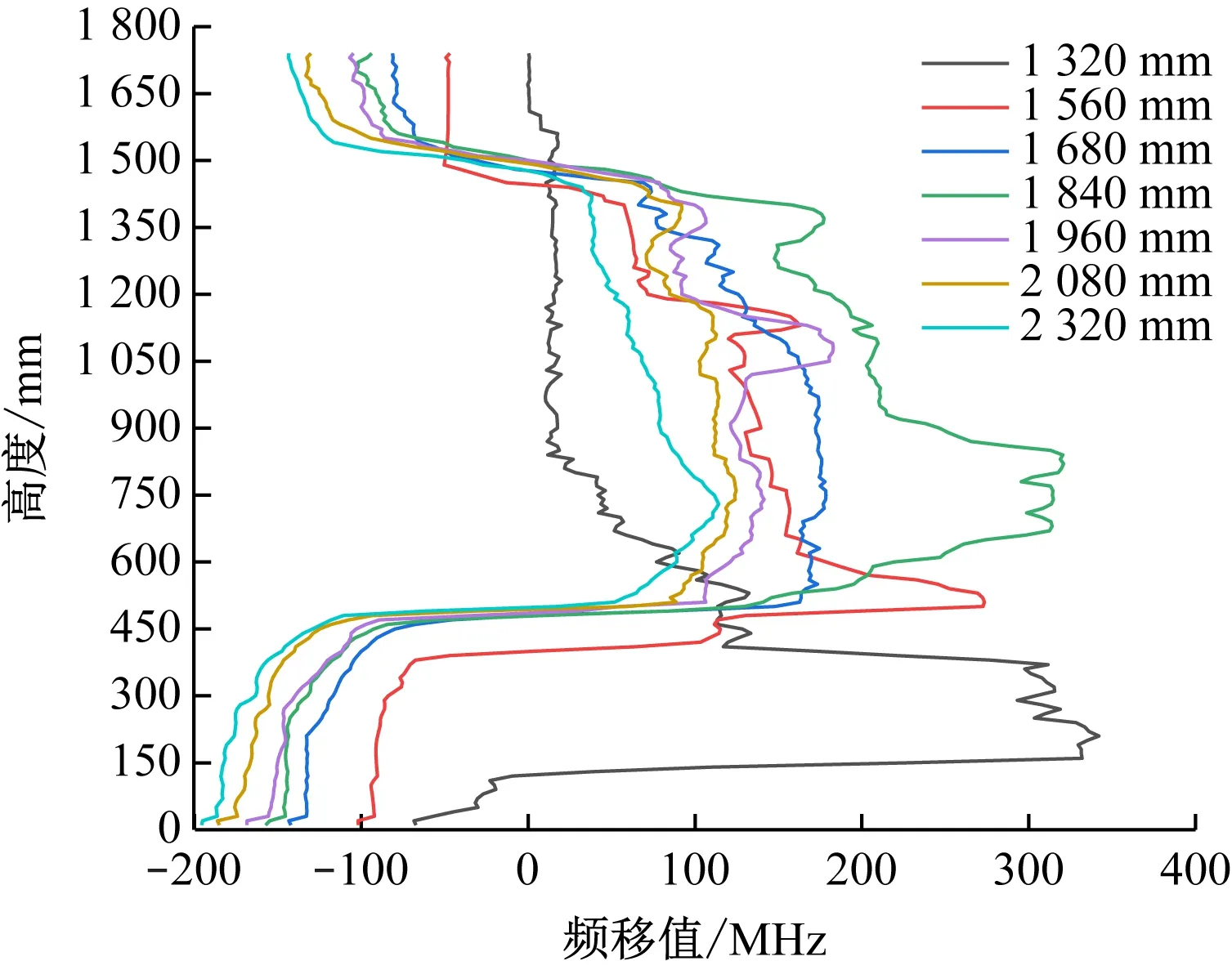
圖7 光纖預測數據整合Fig.7 The optical fiber prediction data integration

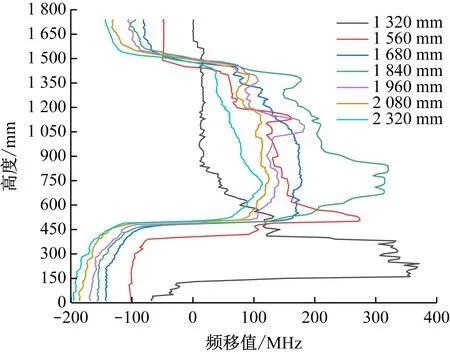
圖8 光纖原始頻移數據Fig.8 The optical fiber raw frequency shift data

4 基于XGBoost模型的礦壓預測

4.1 數據預處理

為了驗證XGBoost模型在預測礦壓規律上的優越性，采用傳統的BP神經網絡模型與XGBoost模型對礦壓進行對比預測。將完整的光纖頻移值轉換為能表征礦壓現象的光纖平均頻移變化度曲線，如圖9所示。根據光纖平均頻移變化度“尖峰”可以表征礦壓的原理，對“尖峰”進行標注，在工作面掘進過程中，共出現14次來壓現象。

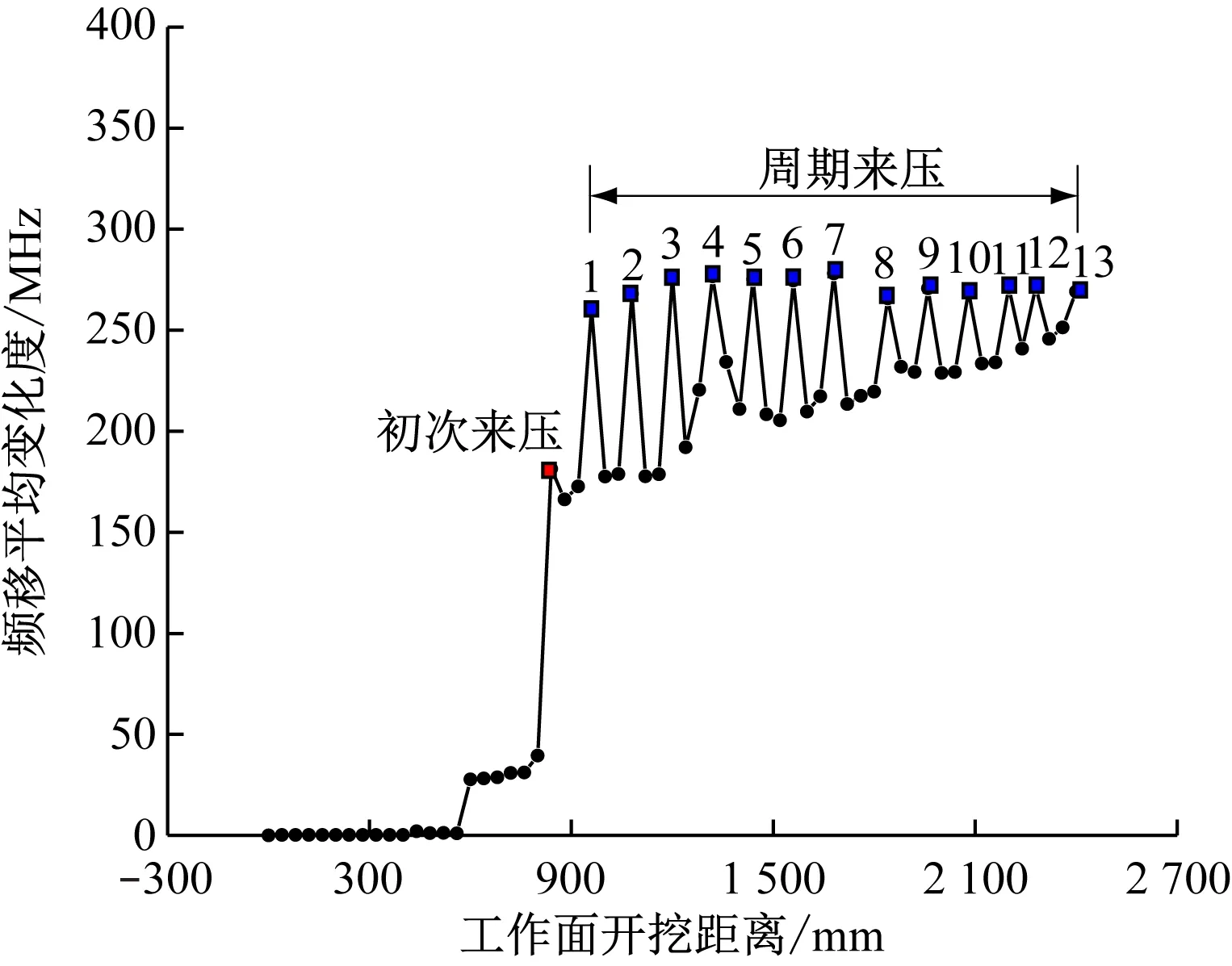
圖9 Fv1光纖平均頻移變化度曲線Fig.9 The average frequency shift curve of Fv1 optical fiber

4.2 數據集構建

基于混沌理論[17]對光纖平均頻移變化度數據進行相空間重構，通過自相關法得到最佳延遲時間τ和嵌入維數v。經實驗得到當v=3，τ=1時，模型達到最優狀態。設P為根據嵌入維數v建立的輸入數據集，Q為根據延遲時間τ建立的輸出數據集,數據集形式為

(11)

式中p為數據集中的數據。

將經過相空間重構的數據集按照4∶1的比例劃分為訓練集和測試集，將訓練集代入模型進行學習，測試集用來評估模型預測效果。

4.3 礦壓預測

采用網格搜索算法對XGBoost模型中樹的深度和數量等超參數進行最優化，當樹的深度為6、樹的數量為60時，可使模型性能達到最優。XGBoost模型和BP神經網絡模型的預測結果如圖10所示。可看出XGBoost模型能準確預測出測試集中所有出現“尖峰”的位置，而BP神經網絡模型只預測出2處“尖峰”的位置，說明XGBoost模型的預測效果優于BP神經網絡模型的預測效果。

計算可得BP神經網絡模型的平均絕對誤差為34.42 MHz，平均相對誤差為23.01%，XGBoost模型的平均絕對誤差為13.60 MHz，平均相對誤差為9.45%，XGBoost模型誤差小于BP神經網絡模型，說明XGBoost模型預測礦壓的準確率優于BP神經網絡模型。

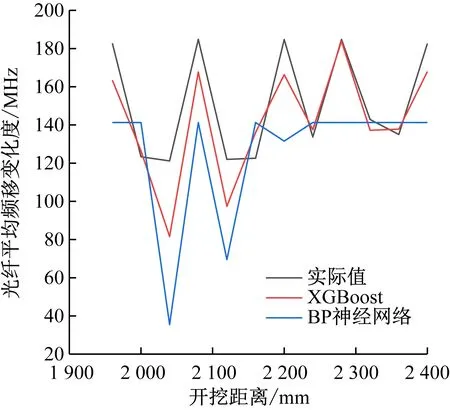
圖10 XGBoost模型和BP神經網絡模型的預測結果Fig.10 Prediction results of XGBoost model and BP neural network model

5 實驗驗證

為驗證使用GRU模型預測缺失值的有效性和采用XGBoost模型預測礦壓的泛化性，將預測出來的缺失數據填補到缺失位置，形成“完整”的光纖頻移值數據，將其轉換為光纖頻移變化度數據后，再使用XGBoost模型進行預測，實驗結果如圖11所示。可看出經缺失值填補后，采用XGBoost模型依然可以準確預測出“尖峰”位置。對XGBoost 模型預測出來的數據與真實數據間的誤差進行統計，可得平均絕對誤差為13.74 MHz，平均相對誤差為9.48%。與使用XGBoost模型預測完整光纖的效果相差不大。綜上所述，使用GRU模型可對缺失的光纖數據進行有效預測，且XGBoost模型在其他數據集中的表現良好。

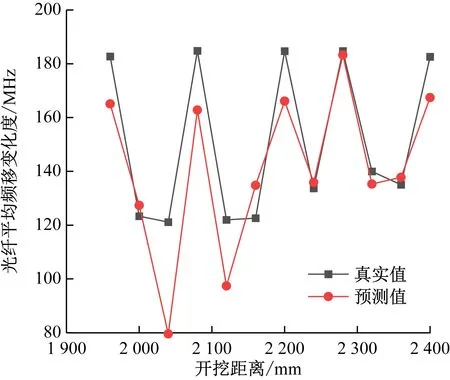
圖11 替換數據預測Fig.11 Replacement data prediction

6 結論

(1) 通過LSTM和GRU模型對光纖下半部分數據進行預測。結果表明，2種模型均可準確預測出光纖下半部分的數據，且GRU模型準確性較LSTM模型準確性高。

(2) 基于表征礦壓規律的相似物理模型實驗測得的光纖頻移數據，使用XGBoost模型對模擬工作面推進下的礦壓進行預測，可準確預測出測試集中所有出現“尖峰”的位置，其平均絕對誤差為13.60 MHz，平均相對誤差為9.45%。

(3) 通過多次采用GRU模型預測其他掘進次數的光纖下半部分數據，用預測結果替換原始監測結果，重新計算光纖平均頻移變化度，經歸一化、相空間重構后代入XGBoost模型進行預測。結果表明，替換后的數據能準確預測出周期來壓，與原始結果基本吻合，其平均絕對誤差為13.74 MHz，平均相對誤差為9.48%。