不同節間長度下鋼桁架結構受力性能研究

王雅文

(廈門中建東北設計院有限公司 福建廈門 361000)

0 引言

鋼桁架結構20世紀60年代在我國首次應用。近年來，隨著各類體育場館、大型機場和會展中心等大型公共建筑的建設日益增多，鋼桁架結構獲得迅速發展，吸引了工程師和學者的廣泛研究。

楊文偉等[1]對4個鋼管桁架結構K形搭接節點足尺試件進行試驗研究，試驗結果表明：K形搭接節點內隱藏焊縫對試件的承載能力影響不大，隱藏焊縫不焊接節點試件的滯回耗能優于隱藏焊縫焊接的節點試件；隱藏焊縫不焊接節點試件的變形是隱藏焊縫焊接節點試件的1.1～1.2倍。黃逸群等[2]以某工業管道支架采用的兩端簡支矩形截面空間鋼管桁架為研究對象，采用非線性有限元法，進行結構整體穩定分析，提出矩形截面空間鋼管桁架整體穩定實用設計方法。趙嘯峰等[3]采用3種方法對4種桁架結構進行連續倒塌動力有限元分析，結果表明：瞬時剛度退化法能夠較準確地模擬桿件失效所引起的結構動力響應，高敏感性桿件失效時，建議采用瞬時剛度退化法。徐琳等[4]對大跨度雙曲面管桁架鋼結構屋蓋施工受力性能進行研究，通過有限元方法對吊裝施工過程進行數值模擬分析，驗算桁架在吊裝過程中支架和主體結構的安全性。陳波[5]等對矢跨比分別為1/4、1/6和1/8的3個拱形桁架屋面進行同步測壓風洞試驗，分析風荷載和結構參數對平面拱形桁架風振響應和等效靜風荷載的影響規律，結果表明：0°風向時，高矢跨比屋面的最大負壓幅值出現在屋頂，而低矢跨比的出現在迎風前緣。

目前國內針對桁架節點、抗連續倒塌、施工受力性能、桁架風振相應等方面做了相關研究，但對于桁架設計參數的研究相對較少。同時，我國2010年發布了《空間網格結構技術規程》JGJ 7[6]，對網架結構的跨高比、短向網格數、相鄰桿件夾角及撓度限值等作了相關規定，但缺少對桁架結構節間長度的設計參數參考取值，不利于桁架結構的發展。本文選取桁架結構作為研究對象，基于實際工程，分析節間長度對桁架的受力、變形性能及含鋼量等的影響規律，提出相應的參考取值范圍，可為廣泛的工程應用提供參考。

1 工程背景及分析模型的選取

某工程位于福建省，其中某棟為單層封閉式游泳池，跨度達61 m×36 m，局部有夾層，其中一側為兩層走廊，底部結構形式為鋼框架結構上部屋面短跨采用單向平面桁架，建筑結構設計使用年限50年，安全等級為二級，抗震設防類別為丙類，抗震設防烈度為7度，基本地震加速度0.1 g，設計地震分組第三組，場地類別為Ⅱ類，特征周期0.45 s，基本風壓為0.8 kN/m2(50年一遇)，地面粗糙度按A類。

結構平面圖如圖1所示，選取圖中虛線范圍單榀平面桁架進行分析。為了簡化模型，作出以下基本假定：

(1)桁架桿件均為直桿；

(2)桁架支座剛接；

(3)桁架間距取7.5 m計算荷載，且荷載均作用在桁架平面內。

簡化模型示意如圖2所示。

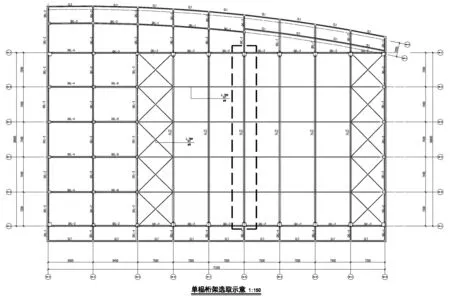
圖1 結構平面圖

圖2 簡化模型示意圖

2 分析模型的建立

采用3D3S(版本V2020.3.20)進行分析，桁架跨度36 m，桁架跨高比取1/15，腹桿采用全斜式，上下弦節間長度分別取1.2 m、1.6 m、2.0 m、2.4 m、2.8 m、3.2 m、3.6 m和4.0 m，上弦桿截面均取A377×14 mm，下弦桿截面均取A530×14 mm，腹桿截面均取A140×10 mm。鋼構件均采用Q355B結構鋼，彈性模量取2.06×105kN/mm2，泊松比取0.3，線膨脹系數取1.2×105，密度取7850 kg/m3，荷載工況及荷載取值如表1所示。

表1 荷載工況及荷載取值

3 結果分析

各桁架跨中和支座處的上、下弦桿及腹桿內力最大值對比如圖3所示，最大位移如圖4所示，構件強度應力比對比如表2所示，整體穩定應力比對比如表3所示，含鋼量對比如表4所示。

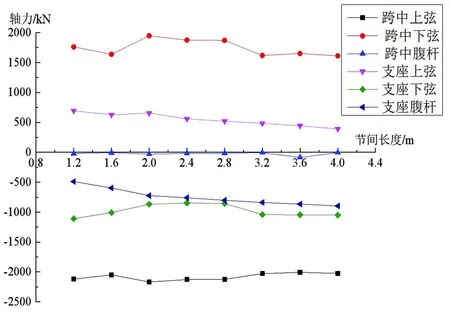
(a)軸力

(b)剪力

(c)彎矩

圖4 不同節間長度桁架最大位移對比

由圖3可知，節間長度L的變化對桁架跨中構件最大內力的影響不大，對支座構件的影響較為明顯。隨著L的增加，支座上弦軸力減小，L=4 m(ln/9，ln為跨度，余同)時支座上弦軸力比L=1.2 m(ln/30)時減小43.6%，影響較大，剪力和彎矩變化不大。增大L，支座下弦軸力先減小后增大，當L=2.8 m(ln/12.8)時最小；剪力和彎矩逐漸減小，L=4 m時支座上弦的剪力和彎矩比L=1.2 m時分別減小57.6%和28.5%，影響較為顯著。支座腹桿軸力隨著L的增加逐漸增大，L=4m時支座腹桿的軸力比L=1.2m時增加83.4%，影響顯著。同時，可以看出，在設計過程中調整節間長度時，應重點關注支座處的受力狀態和構件截面的調整。

由表2可知，增大L使得桁架整體強度應力水平增大；當L=1.2 m時，由于支座下弦桿線剛度過大，導致支座下弦桿應力超限(圖5)，不滿足規范要求，因此節間長度不宜過小。由表3可知，桁架整體穩定應力比隨著L的增加而增大，整體穩定性逐漸下降，當L=4 m時，整體穩定應力比超限，不滿足規范要求，因此節間長度不宜過大。

由圖4可知，隨著L的增加，桁架最大位移逐漸減小。為了進一步分析節點長度對桁架剛度的影響規律，按式(1)分別計算各桁架的抗彎剛度：

P=KΔ

(1)

式中：P為結構所受外荷載，K為桁架抗彎剛度，Δ為桁架豎向變形。

剛度計算結果如圖6所示，由圖可知，桁架剛度隨節間長度的增加而增大，L=4 m時桁架剛度比L=1.2 m時提高18.5%。由于桁架的受力類似于空腹梁，根據上述分析可知，節間長度越大，腹桿與下弦桿的夾角越小，對桁架的抗彎越有利。

由表4可知，增大L桁架含鋼量降低，但對含鋼量的影響逐漸減小。不同節間長度桁架自重與外荷載比值對比如表5所示。由表可知，桁架自重與外荷載的比值約為36%～41%，占比相對較大，分析時不可忽略自重的改變對結構受力和變形的影響。綜上所述，節間長度可取1.6 m～3.6 m，即跨度的1/22～1/10，建議取1/13～1/12。

不同節間長度對應的腹桿間夾角(不包括支座)如表5所示。結合上述分析由表5可知，腹桿間夾角不宜小于30°，也不宜過大，建議取60°。

圖5 L=1.2m時桁架強度應力比

圖6 不同節間長度桁架剛度對比

表2 不同節間長度強度應力比對比%

表3 不同節間長度整體穩定應力比對比 %

表4 不同節間長度桁架含鋼量對比

表5 不同節間長度桁架自重與外荷載比值對比

表6 不同節間長度對應的腹桿間夾角

4 結論

本文針對鋼桁架結構，分析了不同節間長度時桁架結構的受力、變形和含鋼量等的變化規律，得出以下結論：

(1)節間長度的變化對桁架跨中構件最大內力的影響不大，對支座構件的影響較為明顯。隨著節間長度的增加，支座上弦軸力減小，剪力和彎矩變化不大；支座下弦軸力先減小后增大，當節間長度為2.8 m時最小，剪力和彎矩逐漸減小，影響較為顯著；支座腹桿軸力逐漸增大，影響顯著。

(2)增大節間長度，桁架最大位移減小，桁架剛度增大，桁架整體強度應力水平和穩定性應力比增大；但節間長度過小時支座下弦強度超限，過大時整體穩定性不滿足要求。

(3)增大節間長度，桁架含鋼量降低，但對含鋼量的影響逐漸減小。

(4)節間長度可取1.6 m～3.6 m，即跨度的1/22～1/10，建議取1/13～1/12。

(5)腹桿間夾角不宜小于30°，也不宜過大，建議取60°。