電磁發射超高速彈丸氣動特性數值分析 *

馮軍紅，魯軍勇，李 開，李湘平

(海軍工程大學 艦船綜合電力技術國防科技重點實驗室， 湖北 武漢 430033)

電磁發射超高速彈丸是指利用電磁能技術發射一體化彈丸至超高速狀態，其具有初速高(可達6Ma以上)、射程遠(可達200 km以上)、威力大以及發射能量精確可調等優勢，是一種先進的動能殺傷武器[1-3]。作為大空域飛行的超高速彈丸，其氣動減阻以及飛行穩定特性是關鍵，值得深入研究。隨著計算流體力學的發展，采用數值方法計算超高速彈丸的氣動力及力矩逐漸被國內外學者普遍接受，成為研究彈丸氣動特性的重要手段[4-9]。

相對于傳統的低速彈丸，超高速彈丸的飛行空域和速域范圍較大，幾乎覆蓋了大氣層的不同層段，涉及稠密大氣層減阻、稀薄氣體效應以及黏性干擾效應等氣動現象，使得超高速彈丸氣動力、力矩以及壓心變化較大，存在大空域氣動減阻、氣動熱防護和飛行穩定性等諸多問題。近年來，國內南京理工大學等[9-10]單位開展了超高速彈丸的氣動特性研究，重點分析了彈丸的氣動力和氣動熱特性，但缺乏對彈丸再入飛行段大攻角下的氣動特性分析。其他研究單位也較少涉及這一方面的研究。

本文以電磁發射超高速彈丸為研究對象，采用雷諾平均數值方法計算了超高速彈丸的三維氣動流場，并通過風洞試驗數據驗證了數值計算精度。重點分析了超高速彈丸再入段大攻角下的氣動特性，得到了彈丸的非線性氣動參數，為超高速彈丸再入段飛行穩定性研究提供了氣動數據，也為彈丸外形設計提供了參考。

1 數值仿真方法

1.1 控制方程

不考慮體積力，采用Favre平均定常張量形式的N-S方程為：

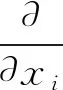
(1)

(2)

(3)

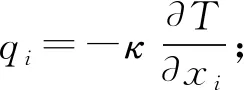
1.2 湍流模型

對于彈丸的外部流場計算，最為常用的湍流模型是S-A(Spalart-Allmaras)單方程模型，詳細的模型說明可見文獻[11]。但是S-A湍流模型在預測分離流方面誤差較大，石磊等[12]對比分析了S-A和k-ωSST湍流模型在預測高速旋轉彈丸氣動特性的精度，指出SST湍流模型在可壓縮分離流預測方面優于S-A模型。SST湍流模型適合用于高速流動和由于逆壓梯度造成的分流流動[13]，并得到了廣泛的應用[9,14]，有關k-ωSST湍流模型的詳細說明可見文獻[15]。本文擬采用這兩種湍流模型計算超高速彈丸的三維流場，并將計算結果與風洞試驗進行對比，同時，采用k-ωSST湍流模型計算超高速彈丸再入段大攻角下的氣動流場。

1.3 計算模型及網格

為減小氣動阻力，采用無翼式布局，流線型外形，見圖1。以彈丸總長L為特征長度，彈丸長細比約為7，尾翼呈“×”型結構，翼厚度為2 mm，斜置安裝于彈丸底部。由于尾翼斜置的原因，使得彈丸并不完全對稱，因此，建立了三維全彈模型，同時考慮超聲速來流，前場流場區域為0.5倍彈長，后場區域為3倍彈長，徑向為1.5倍彈長。采用ICEM CFD軟件進行網格劃分，在彈丸和尾翼壁面處進行網格加密處理，保證壁面y+值位于30～35之間，網格過渡比為1.2，如圖1所示。

(a) 計算模型及對稱面網格(a) Calculation model and grid of symmetry plane

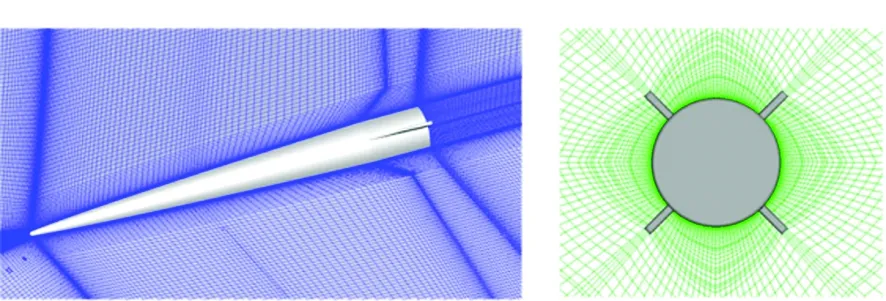
(b) 三維網格結構(b) Three-dimensional grid (c) 尾部剖面網格(c) Tail section grid圖1 計算模型及網格示意圖Fig.1 Computation model and grids distribution

利用有限體積法、基于隱式方法數值求解定常的N-S方程，空間上采用二階迎風格式進行離散，采用AUSM+通量分裂格式，彈丸和彈翼表面采用無滑移的絕熱壁面條件，在來流入口、出口以及周向邊界上均采用壓力遠場邊界條件。整個計算工況見表1。基準工況的大氣壓力為101 325 Pa，溫度為288.15 K，再入工況可取12 km海拔高度的大氣參數，大氣壓力為19 399 Pa，溫度為216.65 K。

表1 計算工況

2 計算結果分析

2.1 數值驗證

2.1.1 網格無關性驗證

為驗證計算網格無關性，在現有模型基礎上劃分了3套不同數量的網格，網格加密方式相同，在彈體壁面附近進行網格加密，粗網格數量為160萬，最小網格尺寸為0.05 mm，最大網格尺寸為4 mm；適中網格數量為260萬，最小網格尺寸為0.02 mm，最大網格尺寸為1.5 mm；精細網格數量為330萬，最小網格尺寸為0.01 mm，最大網格尺寸為1 mm。數值計算結果可見表2，升力系數的相對誤差較小。俯仰力矩系數的相對誤差從210萬加密到330萬時計算結果相差0.06%，這說明網格影響趨于收斂，本文選用適中網格數量滿足計算要求。

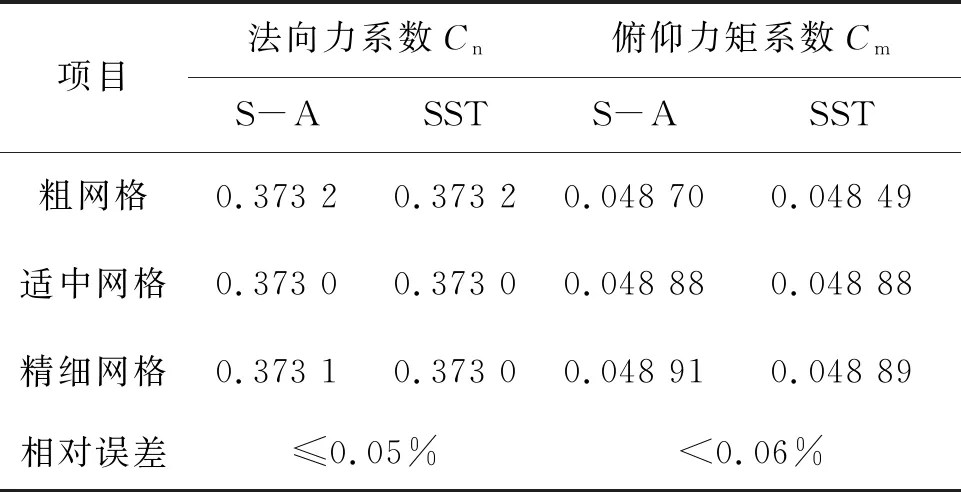
表2 網格無關性數值驗證

2.1.2 數值結果試驗驗證

采用風洞試驗數據驗證數值仿真結果，圖2～4顯示了數值計算和風洞試驗的對比結果，分別對比了高馬赫數下S-A和k-ωSST湍流模型的預測精度。可看出，法向力系數和俯仰力矩系數吻合較好，最大誤差為1.8%。同時兩種湍流模型的預測精度相當。相對于S-A湍流模型，k-ωSST湍流模型的最大誤差為1.7%，略高于S-A模型的預測精度，這是因為法向力系數與俯仰力矩系數主要由氣體壓差產生，黏性項貢獻較小，而兩種湍流模型對壓力項預測精度較高，所以誤差較小。

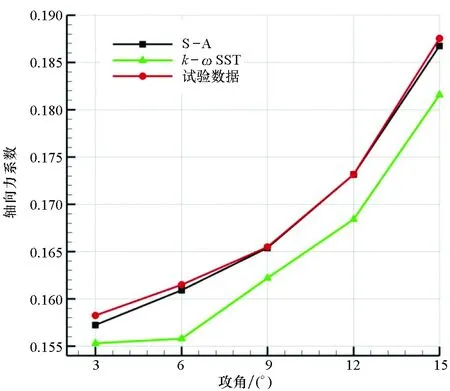
圖2 軸向力系數隨攻角變化曲線(Ma=4)Fig.2 Variation curve of axial force coefficient with angle of attack (Ma=4)

針對軸向力系數，兩種湍流模型的預測精度較低，尤其是k-ωSST湍流模型，最大誤差達到14%，而S-A湍流模型的最大誤差為4.7%。這是由于相對于法向力系數，軸向力系數的黏性項貢獻較大，而湍流渦黏模型在預測湍流黏性項方面的誤差較大，使得計算結果偏差較大。而S-A模型在計算外流場方面具有優勢，因此得到了廣泛的應用。但k-ωSST模型在計算分離流方面更具有優勢[12-15]。因此，本文在基準工況下采用S-A模型；在再入工況下，由于彈丸攻角較大，會產生分離流，采用k-ωSST湍流模型進行計算。

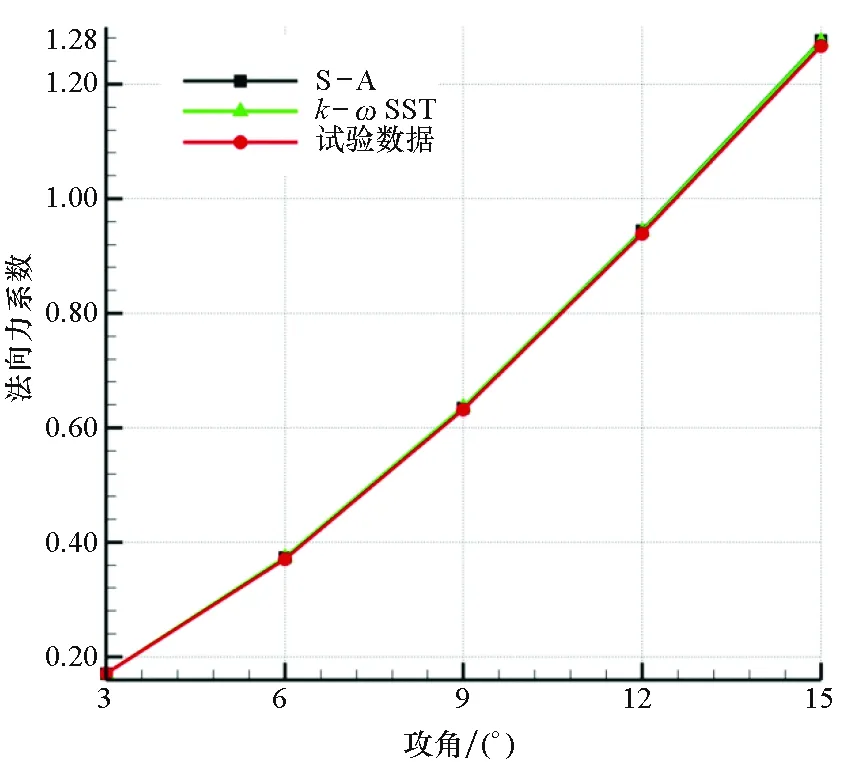
圖3 法向力系數隨攻角變化曲線(Ma=4)Fig.3 Variation curve of normal force coefficient with angle of attack (Ma=4)

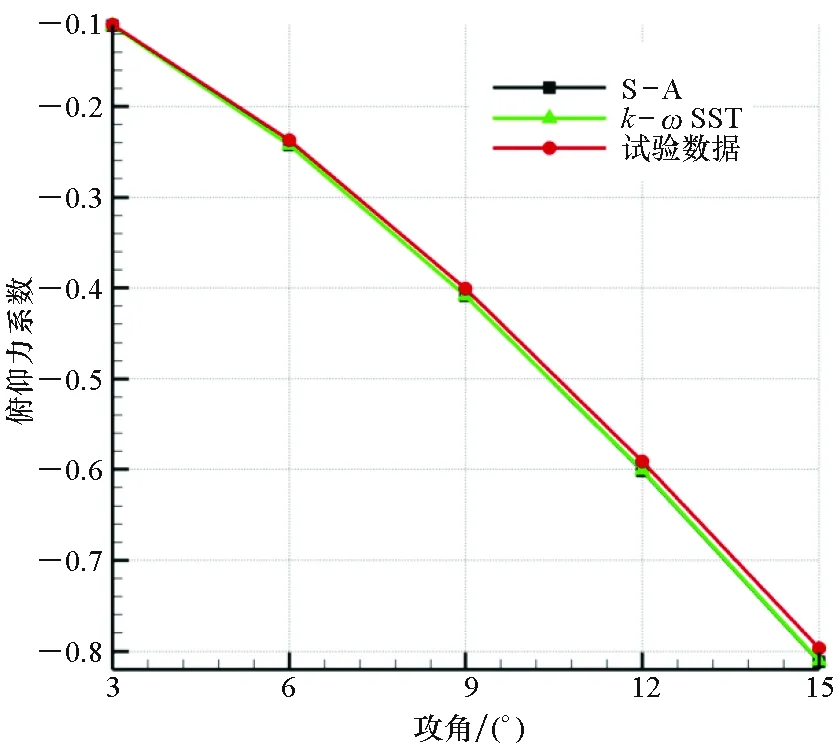
圖4 俯仰力矩系數隨攻角變化曲線(Ma=4)Fig.4 Variation curve of pitching moment coefficient with angle of attack (Ma=4)

2.2 基準工況氣動分析

采用S-A湍流模型的計算結果分析了彈丸氣動流場特性。圖5顯示了攻角3°工況下，不同截面的流場壓力分布云圖。圖5(a)表示0°截面，即彈體的鉛垂面，圖5(b)表示45°截面，即繞彈中心軸旋轉45°的截面。來流在彈體頭部以及彈翼前緣形成脫體激波，但由于彈丸鈍角較小，脫體激波距離較小。激波向周圍空間延伸，且強度逐漸降低。針對高馬赫數來流工況，來流激波角較小，使得激波后的氣流貼近物體壁面。氣流經過彈丸底部先膨脹后壓縮，即底部流場除了由于高速氣流引射作用形成的低壓回流區外，還會形成再壓縮波或激波，流場總壓進一步損失。

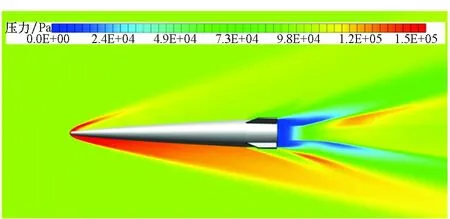
(a) 0° 截面(a) 0° section

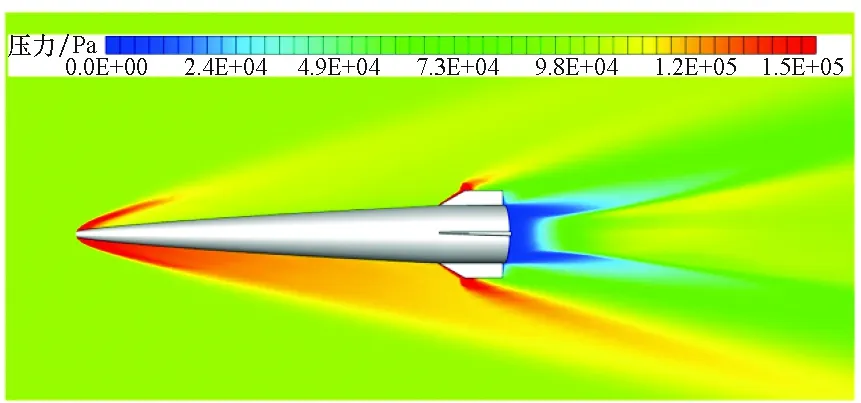
(b) 45° 截面(b) 45° section圖5 不同截面的流場壓力分布云圖(基準工況)Fig.5 Pressure contour in different cross sections (base case)

對于超高速彈丸，氣動阻力主要由三部分組成，即摩擦阻力、波系阻力以及底部阻力。從圖5中可清楚看出波系阻力和底部阻力的產生機理。波系阻力主要是由于氣流經過激波后總壓損失，而底部阻力是由于彈丸底部低壓造成的。圖6顯示了不同攻角下升力系數和阻力系數的變化曲線。升力系數隨攻角接近于線性增長，而阻力系數隨攻角的增長規律呈非線性。

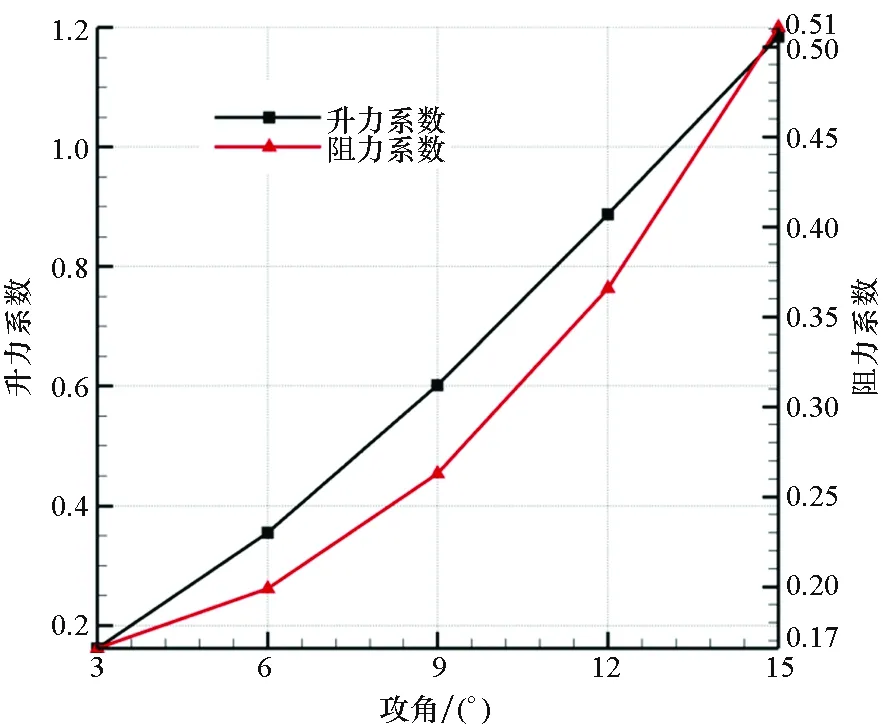
圖6 升力系數和阻力系數隨攻角變化曲線Fig.6 Variation curve of lift and drag coefficient with angle of attack

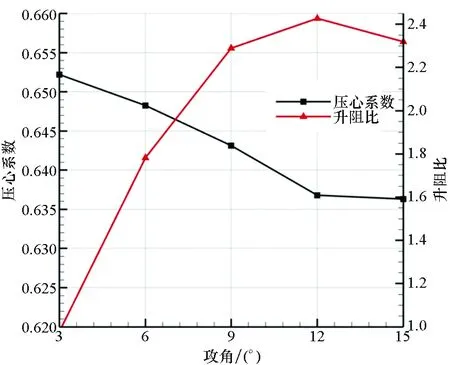
圖7 壓心系數和升阻比隨攻角變化曲線Fig.7 Variation curve of pressure center coefficient and lift drag ratio with angle of attack

圖7顯示了彈丸壓心系數和升阻比隨攻角的變化曲線。隨攻角的逐漸增大，彈丸的壓心系數逐漸變小，說明彈丸的靜穩定裕度降低，在大攻角下，彈丸的穩定性變差，不利于彈丸姿態收斂。此外，升阻比隨攻角先增大后減小，從圖6也可看出，升力系數和阻力系數增長趨勢不同，在大攻角下，阻力系數增長更快，而升力系數相對較慢，導致升阻比增長逐漸變小，存在極值，針對本文研究的彈丸，在Ma=4工況下，攻角在12°左右，升阻比達到最大值。這是因為在大攻角下，氣體流動分離導致誘導阻力急劇增大，使得總阻力增大，最終導致升阻比達到極值，這也符合升阻比變化規律。

2.3 再入工況氣動分析

重點分析了再入工況下彈丸在大攻角下的氣動特性。圖8顯示了攻角25°下，不同截面的流場壓力分布云圖(圖8(a)和圖8(b)的截面定義與圖5相同)。大攻角下，氣體橫向效應比較明顯，彈丸迎風面這一側的激波強度較大，激波后的靜壓急劇增大，而彈丸的背風面由于氣流的分離作用使得壓力逐漸減小。相對于低攻角工況，流場的波系結構對彈丸的影響比重較大，使得彈丸的氣動阻力和升力均增大。

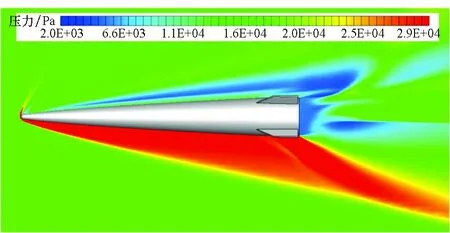
(a) 0°截面(a) 0° section

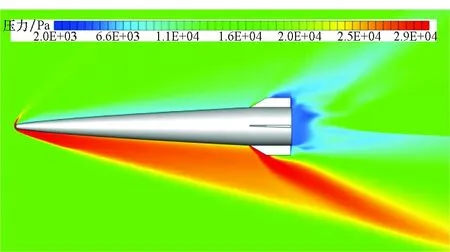
(b) 45°截面(b) 45° section圖8 不同截面的流場壓力分布云圖(再入工況)Fig.8 Pressure contour in different cross sections (reentry case)

圖9對比了攻角3°和攻角25°兩種工況下的底部流場結構。在小攻角下，彈丸來流邊界層未發生分離現象，底部回流區相對對稱，而在大攻角下，由于彈丸背風面的邊界層分離與再附作用，使得來流較為復雜，回流區呈現更為復雜的形態，存在滑移線，形成剪切層。這些流場形態均會影響彈丸的氣動特性和飛行穩定性。

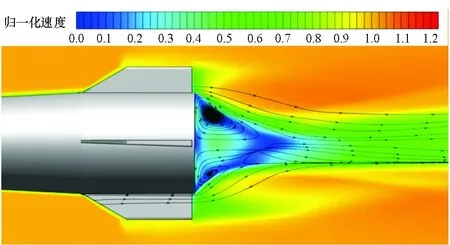
(a) 3° 攻角(a) 3° angle of attack

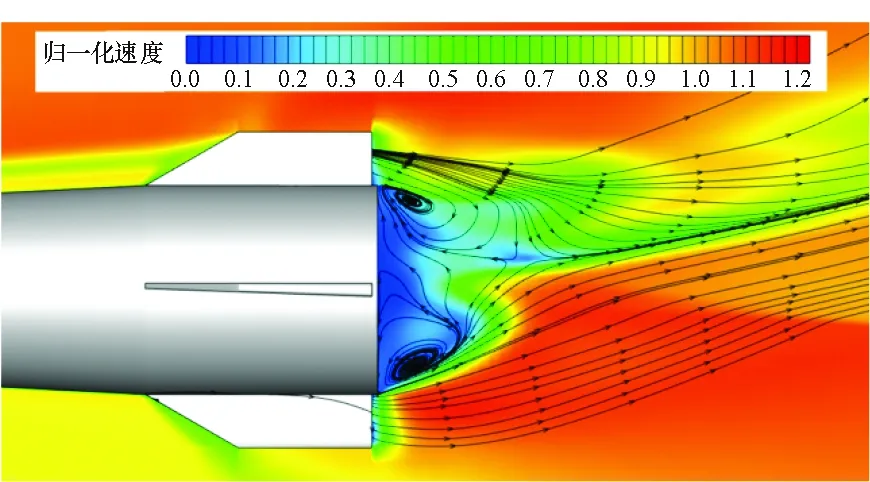
(b) 25°攻角(b) 25° angle of attack圖9 彈丸底部流場速度分布云圖Fig.9 Velocity distribution of flow field at the base of projectile

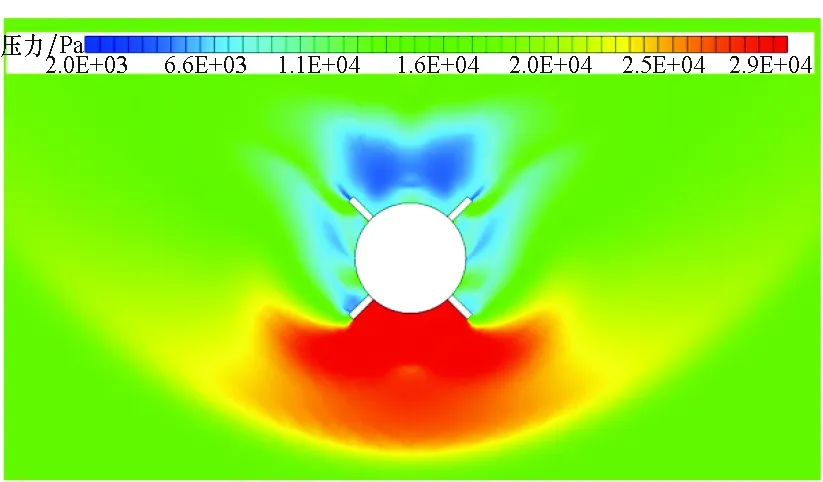
圖10 流向截面的壓力分布云圖(再入工況)Fig.10 Pressure distribution in streamwise section (reentry case)

由于彈丸在大攻角下橫流效應明顯，這里詳細分析了流向截面的壓力分布和流向渦結構分布。圖10顯示了靠近彈丸尾部流向截面的壓力分布云圖，可明顯看出經過激波后的流場壓力突增，類似于乘波結構，而在彈丸的背風面，由于分離作用彈丸表面壓力較小，使得彈丸上下壓差較大，形成氣動升力。圖11對比了不同攻角下的流向渦結構，重點分析橫流繞過彈丸表面后，在背風面的氣流形態，可看出，在小攻角下，氣體橫向流速較小，基本貼體流動；而在大攻角下，橫向氣流繞過彈體后形成脫落渦結構及一對清晰的流向渦，流向渦導致彈丸背風面形成低壓回流區，使得壓力降低。由此可知，大攻角下彈丸的迎風面氣動流場類似于乘波結構，彈丸的背風面流場類似于低壓脫落渦結構。這兩種流場機理均對彈丸的氣動特性存在影響。

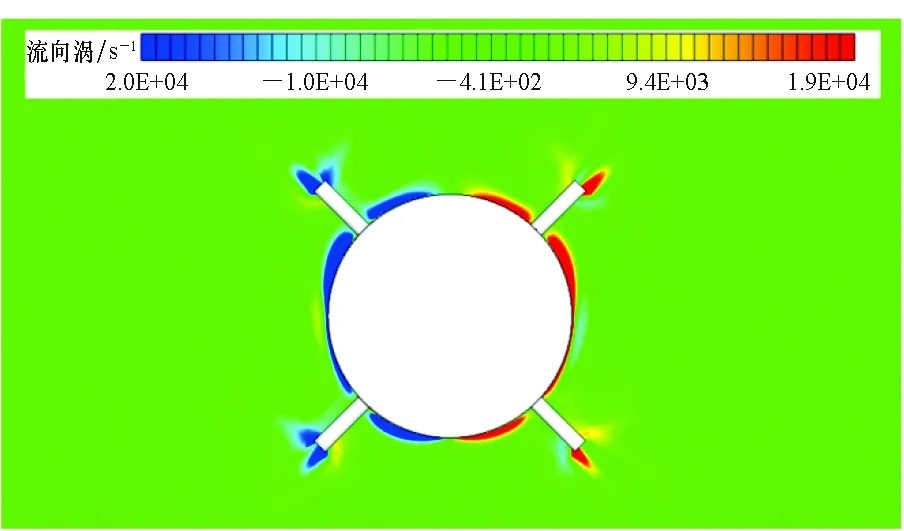
(a) 3° 攻角(a) 3° angle of attack

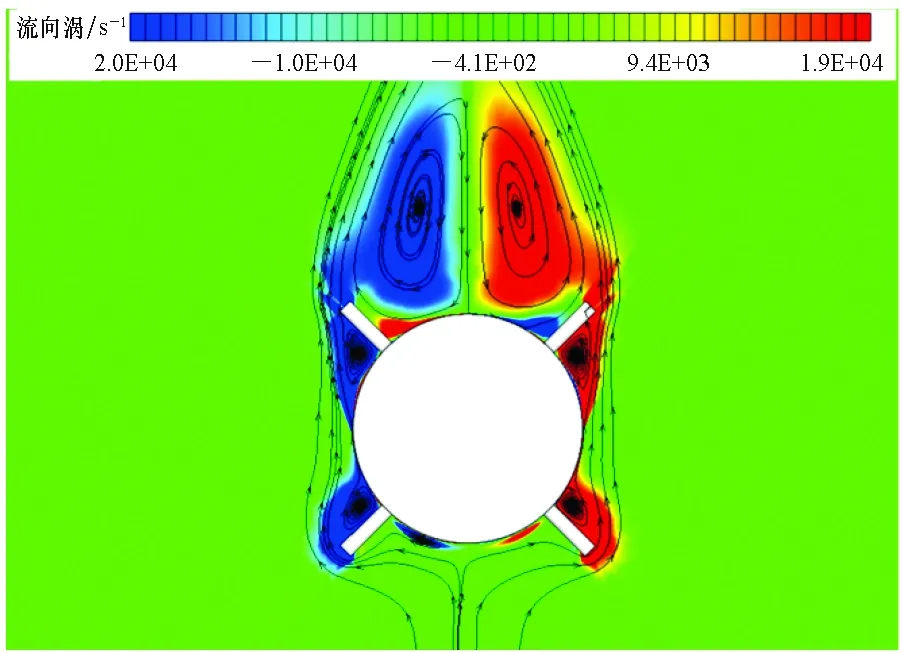
(b) 25° 攻角(b) 25° angle of attack圖11 不同攻角流向截面的流向渦分布云圖Fig.11 Streamwise vortex distribution in different streamwise sections

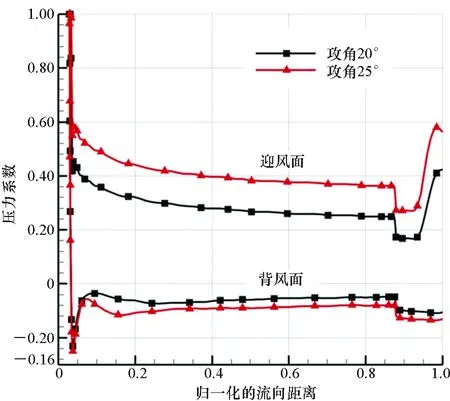
圖12 彈丸表面壓力系數流向變化曲線Fig.12 Pressure coefficient curve on projectile surface

為進一步分析這兩種機理對彈丸氣動特性的影響效果，分析了彈丸表面的壓力系數變化規律，如圖12所示。氣流經過彈丸頭部后，由于激波作用，壓力系數急劇降低，隨后流經迎風面的氣流壓力系數逐漸減小，而背風面的氣流壓力系數變化較小，在靠近尾翼處，由于尾翼的影響，使得壓力系數產生突變。對比不同攻角的壓力系數變化，可看出，隨攻角的增大，迎風面的壓力系數變化較大，而背風面的壓力系數變化相對較小，這說明迎風面的波系結構、流場特性對彈丸的氣動特性影響更為顯著。

圖13顯示了再入工況下(Ma=2)彈丸阻力系數和壓心系數隨攻角變化曲線。隨著彈丸攻角的增大，阻力系數迅速增大，尤其是攻角大于15°后，彈丸的阻力系數增長較快，這說明了大攻角下阻力系數的非線性特性。同時，彈丸的壓心系數也逐漸減小，當攻角大于15°后，由于彈丸壓心系數的前移，使得靜穩定裕度降低了4.5%，這說明再入工況下，彈丸的再入攻角較大，使得彈丸氣動阻力迅速增大，靜穩定裕度急劇降低，彈丸的姿態收斂較慢，從而使彈丸再入段的速度衰減較大。

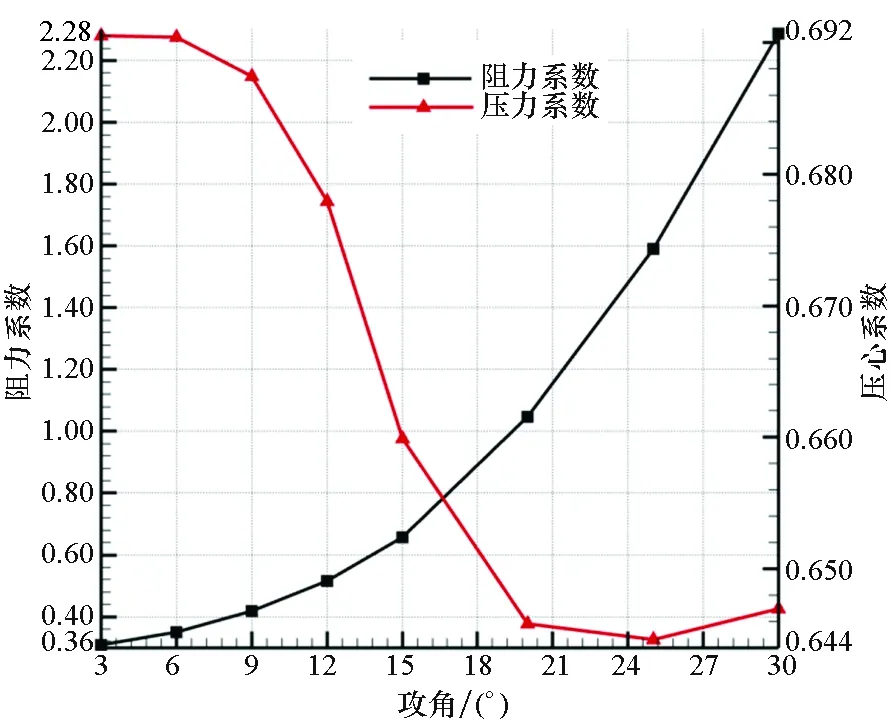
圖13 阻力系數和壓心系數隨攻角變化曲線(再入工況)Fig.13 Drag coefficient and pressure center coefficient change with angle of attack (reentry case)

彈丸的阻力系數是攻角的偶函數，略去四階以上微分項，可寫為：

(4)

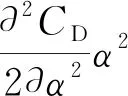
(5)

式中，ΔCD=(CDj-CD(j-1))/(αj-αj-1)，Δα=αj-αj-1。計算結果見表3。初步評估在大攻角工況下，彈丸的阻力二階項是小攻角的2倍，這說明在大攻角下，阻力系數二階項或誘導阻力是彈丸氣動阻力的主要組成部分。

彈丸升力系數是攻角的奇函數，略去高階項，可得：

(6)

可采用一階差分格式評估彈丸氣動升力的非線性特性。計算公式為：

(7)

計算結果可見表3。在小攻角工況下，ΔCL/Δα的值較小，且基本相同，這說明升力系數隨攻角的線性變化特性；在大攻角下，ΔCL/Δα的值是小攻角的2倍，這說明一階線性近似誤差較大，而且隨著攻角的逐漸增大，ΔCL/Δα值逐漸增大，這說明大攻角下彈丸升力系數的非線性特性，高階項的比重逐漸增大，需要引入更高階量才能更為準確地計算氣動參數。

表3 氣動系數與攻角的差分量

3 結論

采用數值計算方法研究了超高速彈丸的氣動流場特性。利用風洞試驗數據對比了兩種湍流模型對超高速彈丸氣動數據的預測能力，計算結果表明兩種湍流模型在計算法向力和俯仰力矩系數等方面的預測精度較高，可達到2%以內，而在阻力系數預測方面，精度較差，S-A湍流模型的預測精度達到4.6%，而k-ωSST湍流模型的預測精度達到14%，這說明S-A湍流模型在預測彈丸外流場特性方面具有較高的精度，這與先前的研究結果一致。

分析了彈丸的底部和橫向流場分布特性。相對于小攻角的氣動流場，大攻角的彈丸底部流場更為復雜，回流區存在滑移線等非定常流場結構。大攻角下的彈丸橫流效應更為明顯，使得高速流場在彈丸背風面形成對稱的脫落流向渦，這些流向渦導致彈丸背風面的壓力降低。在迎風面，激波效應較為明顯，激波后壓力急劇增大，類似于乘波結構，而迎風面的壓力變化對彈丸的氣動阻力和升力特性貢獻作用更大。

最后，分析了彈丸氣動非線性特性，在大攻角下，彈丸的氣動升力和阻力系數呈現明顯的非線性特性，阻力系數明顯增大，而且彈丸的靜穩定裕度也急劇降低，使得彈丸的收斂特性變差，這是引起彈丸再入段速度衰減的主要原因。