改進多線性主成分分析網絡及其在滾動軸承故障診斷中的應用
郭家昕 程軍圣 楊 宇
1.湖南大學機械與運載工程學院,長沙,4100822.汽車車身先進設計制造國家重點實驗室,長沙,410082
0 引言
滾動軸承作為關鍵零部件被廣泛應用于機電設備,滾動軸承出現故障常會造成嚴重的事故和經濟損失,因此,開展滾動軸承故障診斷研究具有重要意義。
滾動軸承的傳統智能診斷方法普遍存在依靠專家知識以及人工提取數據特征工作量大的問題,近年來,卷積神經網絡(convolutional neural network,CNN)作為一種經典深度學習模型[1],可以自主深度挖掘數據特征,成為了滾動軸承智能診斷領域的研究熱點。然而,CNN模型在訓練過程中存在參數爆炸、梯度擴散和反向傳播計算成本高的缺點[2-7],這導致其在滾動軸承故障診斷領域的應用中存在訓練時間較長、訓練小樣本數據易出現過擬合的問題[8]。針對以上問題,CHAN等[9]提出了一種基于CNN的簡單深度學習模型,即主成分分析網絡(principal component analysis network,PCAnet)模型,該模型由卷積層中的PCA濾波器組、非線性處理層中的哈希編碼以及輸出層中的級聯塊狀直方圖組成。PCAnet模型相比于CNN模型,結構有所簡化,無需反向傳播,訓練參數大大減少,一定程度上解決了梯度消失、梯度擴散、訓練時間長的問題以及訓練樣本少時效果不佳的問題。
滾動軸承故障診斷領域中,絕大多數振動信號的各類時頻圖均是彩色圖像,即列、行、色彩模式的三階張量,其中蘊含了豐富的原始信號空間結構信息。傳統的PCAnet模型及其同類方法對圖像進行分類時,均先將多維張量對象轉化成一維向量,再對其進行特征提取,而一維向量則會不可避免地破壞多維圖像中的空間結構,同時也可能造成維度災難[10],因此這種方法在對多維圖像進行自動特征提取時表現欠佳。針對PCAnet模型的這一缺點,WU等[11]提出了多線性主成分分析網絡(mutilinear principle component analysis networks,MPCAnet)模型,該模型是對PCAnet的張量擴展,它從多維空間中提取了圖像的高級語義特征,有效地利用了多維圖像空間結構關系,從而使自動提取的特征盡可能最小化張量對象的類內不變性。MPCAnet卷積層中的MPCA濾波器組對高階張量對象進行處理時不需要對其進行向量化展開,直接輸出低維的同階張量,保留了高階結構,需要估計的參數更少且計算要求更低[12],同時越來越多的學者也證明了張量形式更適合對多維圖像進行分類識別[13]。實踐證明,MPCAnet在多維圖像的分類中取得了更好的效果,僅一層的MPCAnet的分類準確率就超過了兩層的PCAnet[11]。
目前絕大多數基于圖像分類的滾動軸承故障診斷方法,其分類對象都是由運行設備的原始振動信號經過時頻分析產生的時頻圖,工程實際中的原始振動信號通常存在噪聲干擾,具有非平穩和非線性的特點,而MPCAnet在提取數據深層特征時忽略了特征間的非線性關系,不能保證原數據特征線性可分,特征聚類性一般。由于非線性擬合能力較差,所以模型需要更多的訓練樣本數據,而工程實際中滾動軸承的故障樣本往往很難獲得。針對這一問題,本文在MPCAnet的基礎上引入核(Kernel)變換,將原始數據特征映射到了高維核空間實現高度線性可分[14],同時進行降維并訓練得到濾波器組。改進后的模型僅需要少量樣本數據就可以提取到聚類性較強的高維圖像深層特征,泛化能力進一步增強,一定程度上解決了工程實際應用中故障樣本難以獲取的問題。與此同時很大程度上增大了樣本特征之間的差異度,模型的非線性擬合能力得到提高,較原方法的分類精度有所提高。本文提出的改進多線性核主成分分析網絡(multilinear kernal principle component analysis network,MKPCAnet)模型由多線性主成分分析(MPCA)、核主成分分析(KPCA)、二值化哈希層和分塊直方圖四部分組成。將該方法運用到不同類型的滾動軸承故障診斷實例中,結果表明本文提出的基于MKPCAnet的滾動軸承故障診斷方法具有較高的準確性和魯棒性。
1 改進多線性主成分分析網絡
1.1 多線性主成分分析算法
MPCA是PCA從向量到高階張量的一個延伸[15],PCA是將向量投影到向量,MPCA是將張量投影到張量。MPCA可以比PCA捕獲更多原始張量的變化信息和局部特征,通過多線投影進行輸入張量的特征提取。它將原始問題分解為一系列多投影子問題,具有投影結構相對簡單、運算量較少的優勢,適合處理旋轉機械振動信號三維時頻圖像。
將N階張量表示為X∈RI1×I2×…×IN,由N個指標In(n=1,2,…,N)表示,每個指標In都是張量X的n-mode。
張量X與矩陣U∈RJn×In的n-mode積定義為
(1)
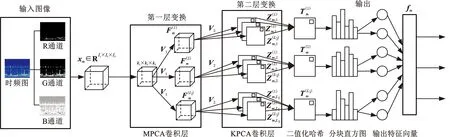
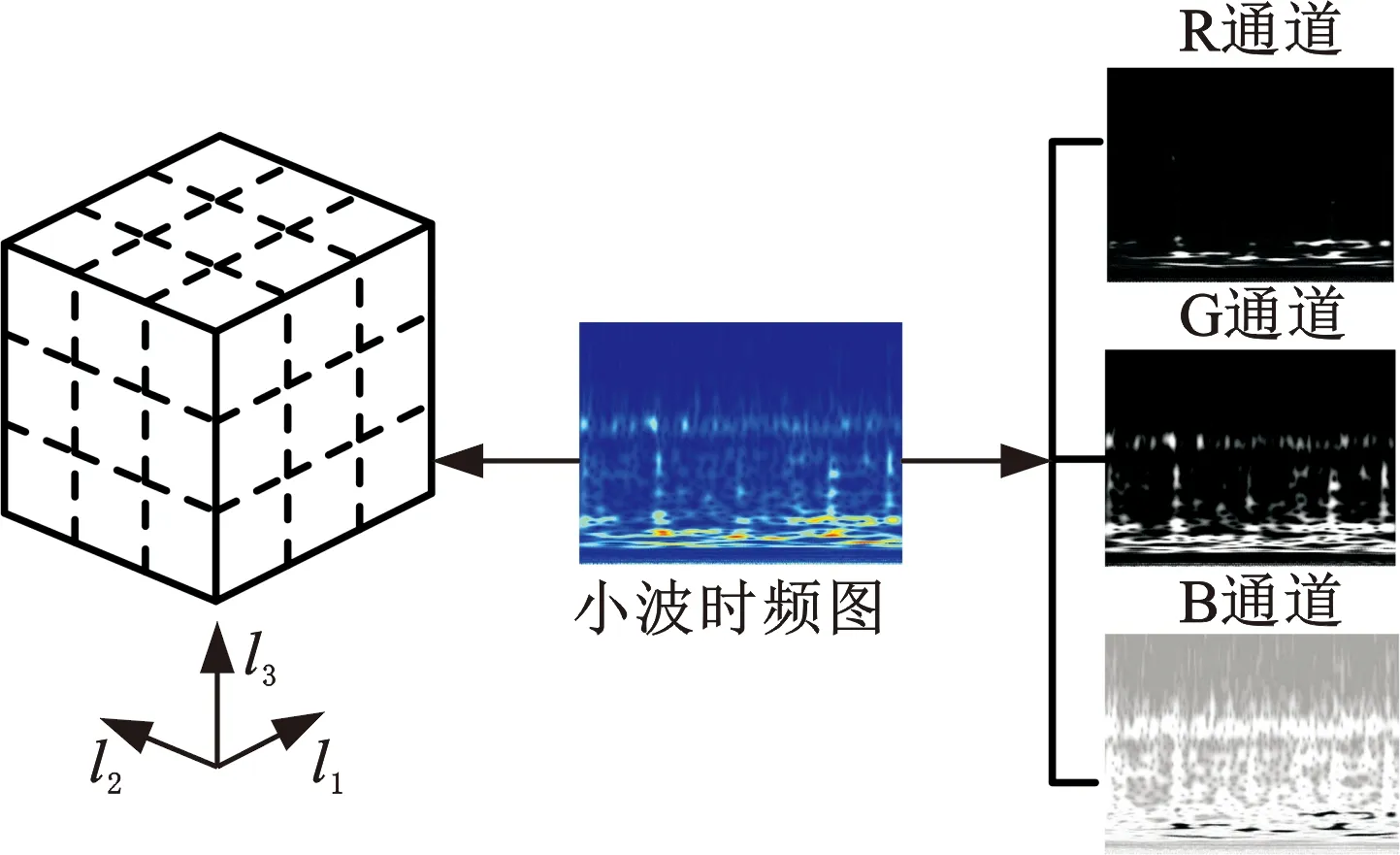
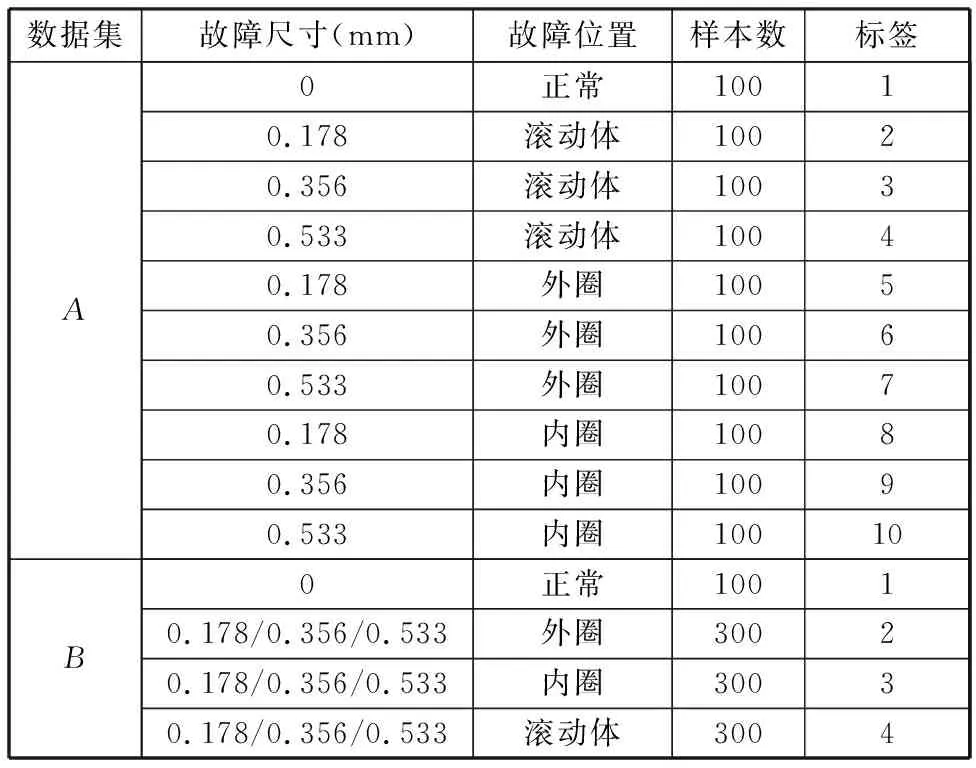
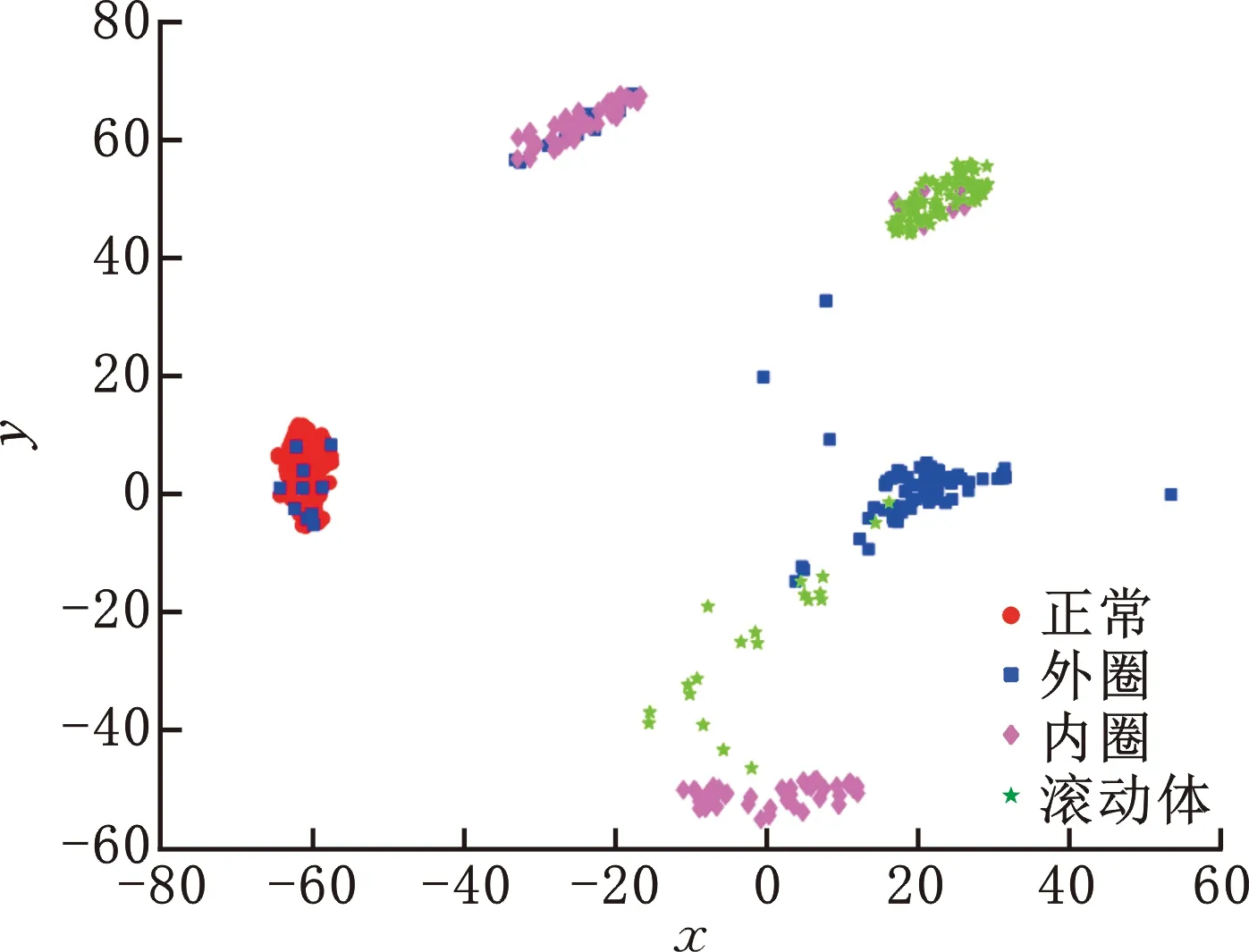
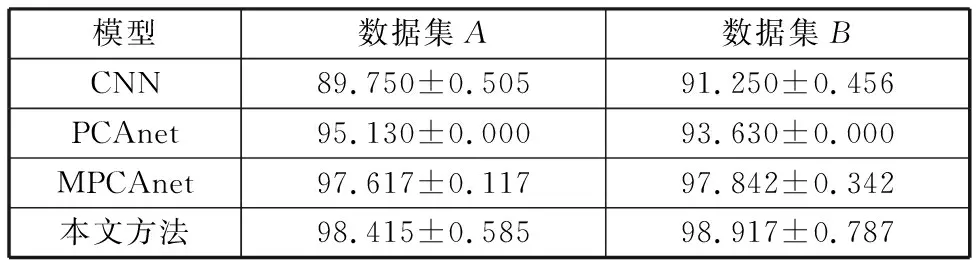
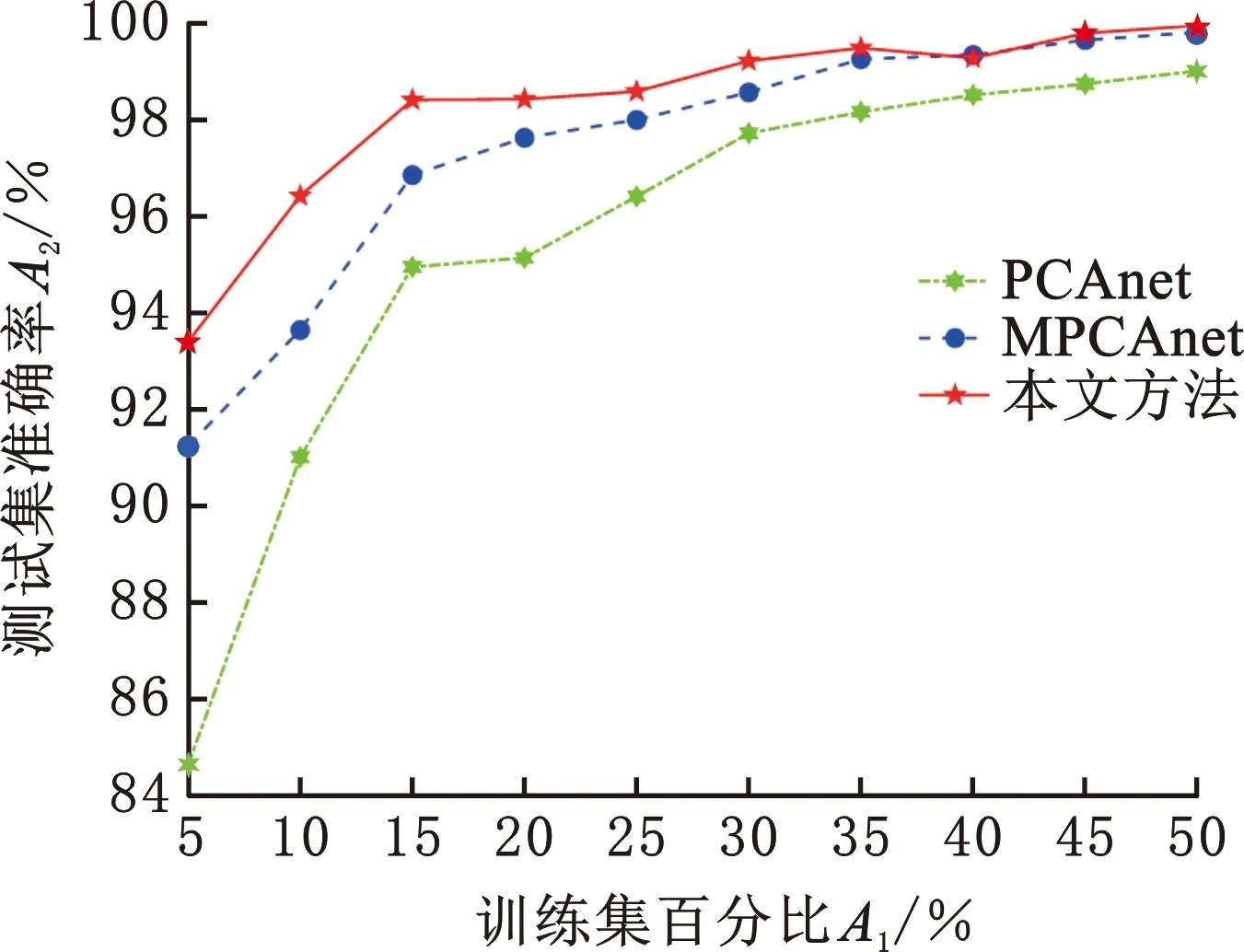
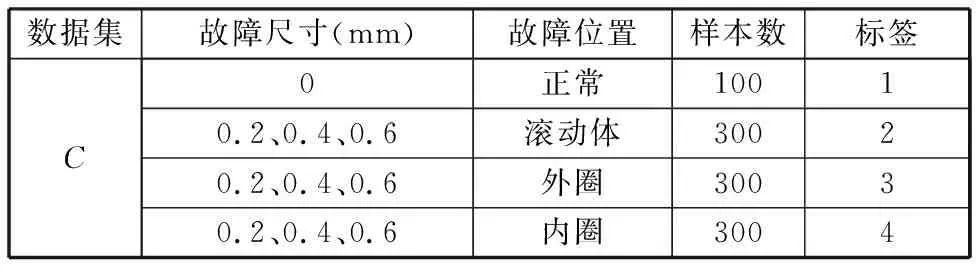
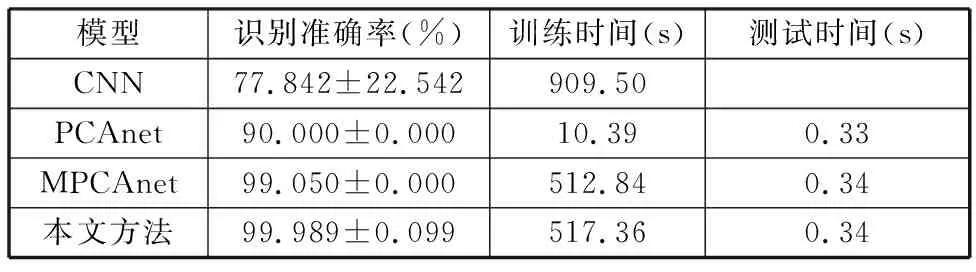
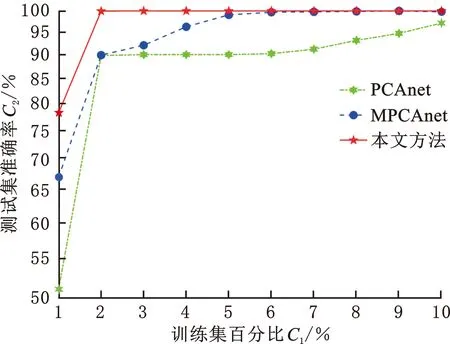
通過投影矩陣{(V(n))T∈RPn×In,n=1,2,…,N},可以將一組(M個)張量對象{Xm∈RI1×I2×…×IN,m=1,2,…,M}映射為另一組(M個)張量對象{Ym∈RP1×P2×…×PN,m=1,2,…,M},其中Pn Ym=Xm×1(V(1))T×2(V(2))T×…×N(V(N))T (2) m=1,2,…,M 式(2)也可以用矩陣的形式表示如下: Xm(n)=V(n)Ym(n)(V(n+1)?V(n+2)?… ?V(N)?V(1)?V(2)?…?V(n-1))T (3) 式中,?表示kronecker積;Xm(n)為張量Xm的n-mode的展開矩陣;Ym(n)為張量Ym的n-mode展開矩陣。 MPCA的目標是確定滿足總張量散射ψY最大化條件的N個投影矩陣{V(n)∈RPn×In,n=1,2,…,N},即 {V(n)}=argmaxV(1),V(2),…,V(N)(ψY) (4) 式(4)的解法如下。令{V(n),n=1,2,…,N}為式(4)的解,其他投影矩陣為V(1),…,V(n-1),V(n+1),…,V(N),矩陣V(n)由Pn個特征向量組成,對應于如下矩陣的最大的Pn個特征值: (5) Vφ(n)=V(n+1)?V(n+2)?…V(N)? V(1)?V(2)?…?V(n-1) (6) Xm(n)由式(3)給出。 最終得到了投影矩陣{V(n),n=1,2,…N}和投影后的張量Ym。 本文提出的改進多線性主成分分析網絡模型由MPCA濾波器組、KPCA濾波器組、二值化哈希層以及分塊直方圖層四部分組成,模型結構示意圖見圖1。 圖1 改進主成分分析網絡模型結構示意圖Fig.1 Flowchart of impoved multilinear principal component analysis network 1.2.1第一層卷積:MPCA層 MPCA層對應卷積神經網絡中的第一層卷積層,類似于神經元局部感受野,起權值共享的作用。 (7) (8) 1.2.2第二層卷積:KPCA層 MPCA層只進行線性變換,非線性擬合能力較差,故引入KPCA算法,當其核函數是非線性核時,能將線性不可分的數據映射到高維空間的線性子空間中,使得數據線性可分。輸入張量數據在MPCA層進行卷積操作后得到第一層特征并輸出到第二層,在第二層被映射到高維核空間中進行特征學習。 KPCA層對應卷積神經網絡中的第二層卷積層。所有輸入圖像經過第一層變換后得到的特征值矩陣可以看作L1×M幅大小為I1×I2的“圖像”,接著用第二層設置的大小為k1×k2的濾波器滑塊遍歷每幅圖像Fi∈RI1×I2,i=1,2,…,L1×M,上述k1和k2均為奇數且1 yi,1,yi,2,…,yi,I1I2∈Rk1k2 (9) 中心化式(9)中的列向量值,得 (10) (11) i=1,2,…,L1M 分別求局部特征矩陣Yi的協方差矩陣: (12) 接著求取L1M個協方差矩陣的平均矩陣: (13) (14) 其中,σ是實參數。接著對矩陣K取均值可得 (15) (16) Zi,j,h∈RI1×I2 (17) i=1,2,…,M;j=1,2,…,L1;h=1,2,…,L2 1.2.3輸出層:哈希和直方圖 fm= (18) 將網絡輸出得到的特征向量fm作為SVM分類器的輸入,訓練分類器,進一步輸入測試圖像進行分類。 基于改進多線性主成分分析網絡的滾動軸承故障診斷具體步驟如下: (1)采用加速度傳感器采集滾動軸承原始振動信號,本文選取小波變換的方法將振動信號轉化為小波時頻圖。由其他方法變換得到的時頻圖像也可以作為本模型的輸入對象。由于morlet小波的沖擊適應性好[17],故本文選用morlet小波作為小波基函數進行連續小波變換來獲得一維時間振動信號的時頻圖,為減少運算量,時頻圖大小統一處理為64×64×3,如圖2所示。 圖2 三階張量小波時頻圖Fig.2 Third-order tensor wavelet time-frequency images (2)根據不同輸入數據集的特性,對比分析確定模型的參數。MKPCAnet模型參數包括:每層濾波器數目、模型層數、輸出層中局部直方圖塊大小、塊重疊區域比率以及KPCA層中的高斯核參數σ。 (3)將三維彩色小波時頻圖作為模型輸入,樣本劃分為訓練集和測試集,通過訓練集來構建最優MKPCAnet故障診斷模型,驗證測試集識別精度,達到故障診斷的目的。 實驗1數據來自美國凱斯西儲大學軸承數據中心。采用型號為6205-2RS SKF的深溝球軸承,采樣頻率為48 kHz,每4800個采樣點劃分為一個樣本。將樣本進行連續小波變換所用尺度序列的長度設置為256,尺度范圍為6~1536,得到每個樣本的小波時頻圖。為保證模型性能評價的客觀全面,數據集A用來識別故障類型及故障程度,負載設置為0HP,共1000個樣本;數據集B只用來識別故障類型,每類故障由不同故障程度樣本組合而成,負載設置為3HP,共1000個樣本。故障類型見表1。 表1 軸承數據樣本 將樣本的三維彩色小波時頻圖作為CNN、PCAnet、MPCAnet以及本文提出方法MKPCAnet的輸入。其中,CNN網絡結構選取經典的AlexNet框架,包括5層卷積層和3層全連接層,輸入圖片大小設置為AlexNet網絡固定輸入格式227×227×3。PCAnet、MPCAnet以及MKPCAnet的輸入圖片大小統一處理為64×64×3。通過對比分析確定各自分類效果最優時的模型參數:三者均采用2層結構,每層濾波器數目均為8,兩層濾波器的大小均為7×7。PCAnet輸出層中局部直方圖塊大小為7×7,MPCAnet和MKPCAnet輸出層中局部直方圖塊大小為24×32,三者塊重疊區域比率均為50%。MPCAnet第一層為MPCA濾波層,第二層為PCA濾波層;MKPCAnet中的KPCA濾波層選擇高斯核函數,通過對比分析確定效果最佳時的高斯核參數σ=6。 為了直觀地展示本文提出模型的優越性能,使用t分布隨機嵌入(t-SNE)算法對每種網絡模型學習后的樣本特征進行可視化處理。選取數據集B的四種故障類型(每類故障90個樣本)進行展示。對比方法包括CNN學習特征、PCAnet學習特征、MPCAnet學習特征和本文提出方法的學習特征,特征可視化結果如圖3所示。結果表明,相比CNN、PCAnet和MPCAnet,本文提出的MKPCAnet模型深度學習得到的特征在同類故障樣本中聚類性更強,異類故障樣本間的距離更遠,可以更清晰地描述和區分不同故障狀態下的軸承信號。 (a) CNN 分別在數據集A、B上進行實驗,每種故障類型均取20%作為訓練集,剩余樣本作為測試集。取10次獨立實驗的平均準確率進行展示,結果見表2。 表2 識別準確率 由表2可以看出,PCAnet較傳統使用隨機梯度下降(SGD)優化算法進行梯度反向傳播的CNN相比,可以在輸入圖像尺寸更小、網絡層數更淺的情況下更精準地識別不同的故障類型和不同程度的故障。基于PCAnet模型進行改進的MPCAnet模型的分類準確率進一步提高。而本文提出的MKPCAnet在數據集A、數據集B中均取得了最高的識別準確率,這是由于MPCA層更有效地利用了多維圖像的空間結構關系,加強了對圖像高級語義特征的提取,KPCA層則提高了模型的非線性擬合能力,這一效果在設置負載的數據集B的測試結果中尤為明顯。 為了驗證本文提出方法的泛化能力,將數據集A采用不同數量的樣本作為訓練集,其余樣本作為測試集,觀察測試集的準確率。每種模型進行獨立重復10次實驗,平均分類精確率如圖4所示。 圖4 識別精度隨訓練集樣本量變化Fig.4 Recognition accuracy changes with the sample size of training set 由圖4可以看出,本文提出方法的準確率高于其他同類方法,同時優于CNN。在小樣本訓練的情況下,KPCA的引入對模型的改善尤為明顯。本文提出的方法準確率較PCAnet提高了8.63%,較MPCAnet提高了3.03%,在每類僅有5%訓練樣本的情況下也能保證測試集達到93%以上的準確率,每類15%訓練樣本時測試集準確率達到了98%以上。說明該方法在小樣本訓練下表現優異且有著良好的泛化能力,一定程度上緩解了工程實際中故障樣本難以獲取的問題。 實驗2數據來自湖南大學旋轉機械故障試驗臺的滾動軸承數據,試驗臺架如圖5所示。在試驗臺上,滾動軸承型號為6205-2RS SKF,通過激光切割技術模擬了內圈故障、外圈故障和滾動體故障。故障尺寸分別為0.2 mm、0.4 mm、0.6 mm,轉速為986.1 r/min,采樣頻率為10 kHz,每條信號的長度為10 000個采樣點,連續小波變換參數與實驗1相同。 圖5 旋轉機械故障試驗臺Fig.5 Rotating machinery failure test device 為更真實地模擬工程實際運行條件,統一將施加載荷設置為2 kN。為驗證本文提出方法在非平穩工況下的診斷魯棒性,統一給所有信號樣本添加10 db高斯白噪聲,獲取的樣本描述見表3。 表3 軸承數據樣本 各模型參數設置與實驗1相同。每一類故障類型取5%的樣本量作為訓練集,剩余樣本作為測試集。在處理器型號為IntelCorei7-8550U CPU @1.80 GHz的PC機上,基于MATLAB2018b平臺記錄訓練時間和測試時間,實驗結果如表4所示。 表4 識別準確率及平均運行時間 由表4可以看出,本文提出的MKPCAnet方法依舊表現出最高的識別準確率。值得一提的是,所有方法的訓練時間相較CNN都有大幅縮短。雖然MKPCAnet的訓練時間相較于結構更為簡單的PCAnet和MPCAnet有所增長,但測試時間均在0.3 s左右,能夠滿足工程實踐中的診斷要求。 進行10次隨機獨立重復實驗,觀察測試集準確率隨訓練集樣本量變化的趨勢,訓練集樣本量從每類故障樣本量的1%到10%依次遞增,結果如圖6所示。本文提出方法仍擁有最好的識別效果,不僅識別精度最高而且表現穩定,具有較好的魯棒性。對于本文提出的方法,當每類故障僅取2%的樣本量作為訓練集時,測試集就可以達到99.96%以上的準確率,遠高于其他方法,滿足工程實際應用需求。 圖6 識別精度隨訓練集樣本量變化Fig.6 Recognition accuracy changes with the sample size of training set 本文提出一種改進的多線性主成分分析網絡并用于滾動軸承故障診斷。改進后的模型由MPCA濾波器組、KPCA濾波器組、二值化哈希層以及分塊直方圖層組成。該網絡使用張量對高維圖像進行自動特征提取,充分利用了高維圖像的空間結構關系,有效提取了圖像的高級語義特征。在此基礎上引入了核主成分分析的方法,提高了模型的非線性擬合能力,進一步提高了分類精度,在小樣本訓練和有噪聲干擾的情況下,模型在分類性能和泛化能力上的提高尤為突出,有效緩解了工程實際中故障樣本難以獲取、信號采集過程振動噪聲干擾等問題帶來的診斷壓力。實驗結果表明本文提出的方法識別性能和魯棒性均高于傳統方法,對傳統基于CNN模型的深度學習識別方法提出了挑戰,對實際工程應用有重要參考意義。 本研究仍有一部分工作尚可繼續深入研究,例如:可進一步研究模型中不同層數、不同濾波器尺寸和不同濾波器個數等參數對模型性能的影響,分析原因;可采用多種時頻分析方法處理得到不同類別的時頻圖像,分別輸入本模型橫向對比診斷效果,找到更合適的信號預處理方法;可嘗試將多源異構信號、多通道信號組成的張量對象作為本模型的輸入進行故障診斷等。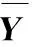
1.2 改進多線性主成分分析網絡
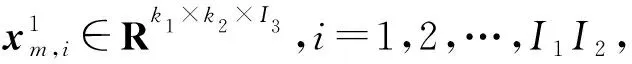
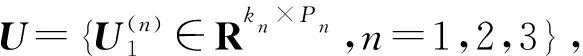
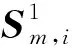
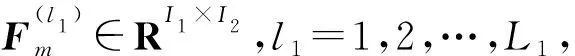
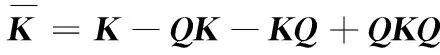
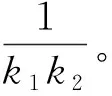
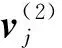
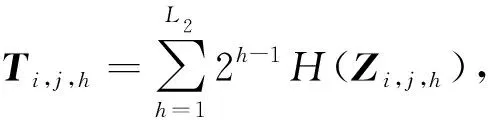
2 MKPCAnet模型滾動軸承故障診斷
3 實驗數據分析

4 結論

