迎角受限的高超聲速飛行器固定時(shí)間魯棒控制
董澤洪,李穎暉,呂茂隆,趙子龍,裴彬彬
(1. 空軍工程大學(xué)航空工程學(xué)院,西安 710038; 2. 空軍工程大學(xué)研究生院,西安 710038;3. 空軍工程大學(xué)空管領(lǐng)航學(xué)院,西安 710051; 4. 荷蘭代爾夫特理工大學(xué)電氣工程、數(shù)學(xué)和計(jì)算機(jī)科學(xué)學(xué)院,代爾夫特 999025)
0 引 言
高超聲速飛行器(Hypersonic flight vehicle,HFV)因其飛行速度快、機(jī)動(dòng)性強(qiáng)、突防能力好等特點(diǎn),具有重要的軍事價(jià)值和民用價(jià)值,受到國(guó)內(nèi)外學(xué)者的廣泛關(guān)注[1-5]。但由于HFV具有強(qiáng)非線性、強(qiáng)耦合、非最小相位的特性,且面臨復(fù)雜快時(shí)變的飛行環(huán)境、大飛行包線內(nèi)實(shí)際的氣動(dòng)參數(shù)與地面風(fēng)洞/仿真所得的氣動(dòng)參數(shù)存在偏差等原因,HFV的飛行控制系統(tǒng)必須具備快速反應(yīng)能力、魯棒性和抗干擾能力[6-7]。另外,超燃沖壓發(fā)動(dòng)機(jī)的工作狀態(tài)與迎角的大小密切相關(guān),迎角必須滿足一定的約束[8]。因此,HFV的飛行控制系統(tǒng)設(shè)計(jì)是一個(gè)重要而極具挑戰(zhàn)性的課題。
為了應(yīng)對(duì)高超聲速飛行器模型不確定的問題,魯棒控制[9-10]、滑模控制[11]、神經(jīng)網(wǎng)絡(luò)控制/模糊控制[12-13]等方法被提出。這些方法雖能處理模型不確定HFV的控制問題,但它們忽略了閉環(huán)系統(tǒng)跟蹤誤差的收斂速率。對(duì)于具有非最小相位特性、高動(dòng)態(tài)、高機(jī)動(dòng)性的HFV,跟蹤誤差的收斂速率彌足重要,誤差收斂的慢不僅會(huì)影響系統(tǒng)的控制性能,嚴(yán)重時(shí)還會(huì)導(dǎo)致系統(tǒng)失穩(wěn)[14]。為了提高HFV系統(tǒng)跟蹤誤差的收斂速率,減少跟蹤誤差的收斂時(shí)間,有限時(shí)間穩(wěn)定定理被應(yīng)用到HFV跟蹤控制器的設(shè)計(jì)中,在指數(shù)收斂控制器的基礎(chǔ)上增加了關(guān)于跟蹤誤差的分?jǐn)?shù)冪次項(xiàng)(冪指數(shù)在0到1之間)[15-17]。然而,有限時(shí)間控制器的誤差收斂時(shí)間與系統(tǒng)的初值有關(guān),在系統(tǒng)初值不能被準(zhǔn)確獲悉的情形下,難以準(zhǔn)確計(jì)算跟蹤誤差的收斂時(shí)間。為了解決收斂時(shí)間的初值依賴問題,固定時(shí)間跟蹤控制器被提出,它在有限時(shí)間控制器的基礎(chǔ)上又增加了一個(gè)關(guān)于跟蹤誤差的分?jǐn)?shù)冪次項(xiàng)(冪指數(shù)大于1),使得跟蹤誤差的收斂時(shí)間不依賴于系統(tǒng)初值[18-20]。有限時(shí)間控制器和固定時(shí)間控制器在提高系統(tǒng)收斂速率的同時(shí),也會(huì)帶來一些問題,例如控制律中關(guān)于跟蹤誤差的分?jǐn)?shù)冪次項(xiàng)(冪指數(shù)在0到1之間)求導(dǎo)時(shí),產(chǎn)生跟蹤誤差的負(fù)次冪項(xiàng),在跟蹤誤差等于零時(shí),這一項(xiàng)將會(huì)變得無窮大,造成閉環(huán)系統(tǒng)的崩潰,即所謂的奇異值問題。因此,在設(shè)計(jì)固定時(shí)間控制器時(shí)應(yīng)避免奇異值問題。
從實(shí)際角度看,超燃沖壓發(fā)動(dòng)機(jī)推進(jìn)系統(tǒng)的工作狀態(tài)對(duì)高超聲速飛行至關(guān)重要,而超燃沖壓發(fā)動(dòng)機(jī)推進(jìn)系統(tǒng)的工作狀態(tài)與高超聲速發(fā)動(dòng)機(jī)的迎角密切相關(guān)。在一定的迎角范圍內(nèi),超燃沖壓發(fā)動(dòng)機(jī)涵道才能獲得足夠的進(jìn)氣量,從而保證超燃沖壓發(fā)動(dòng)機(jī)穩(wěn)定、有效地工作[8]。為了在全飛行包線內(nèi)將迎角限制在一定范圍,文獻(xiàn)[8]和[21]提出了一種基于障礙函數(shù)的HFV迎角受限控制器,然而僅考慮了對(duì)稱時(shí)不變的迎角限制,在設(shè)置限制時(shí)也只能設(shè)置為最小的迎角限制,在全飛行包線內(nèi)這樣的考慮是相對(duì)保守的。文獻(xiàn)[22]基于障礙函數(shù)提出了一種考慮約束的高超聲速飛行器制導(dǎo)與控制一體化設(shè)計(jì)方法。文獻(xiàn)[23]考慮了HFV飛行條件的變化,提出了一種考慮非對(duì)稱時(shí)變迎角約束的自適應(yīng)控制方法。然而,上述方法中跟蹤誤差的收斂速率問題沒有被考慮。
據(jù)作者所知,尚未有關(guān)于考慮非對(duì)稱時(shí)變迎角限制的HFV非奇異固定時(shí)間跟蹤控制方法被公開報(bào)道。因此,本文為HFV設(shè)計(jì)了一種新型考慮非對(duì)稱時(shí)變迎角限制的非奇異固定時(shí)間跟蹤控制器,主要?jiǎng)?chuàng)新點(diǎn)歸納如下:
1)提出了一種跟蹤誤差快速收斂的迎角受限跟蹤控制方法,相比于現(xiàn)有的HFV迎角受限文獻(xiàn)[8]、[21-23],本文方法可以使跟蹤誤差在固定時(shí)間收斂至零的任意小鄰域,提升了系統(tǒng)的穩(wěn)定速度。
2)設(shè)計(jì)了一種光滑切換開關(guān)函數(shù),避免了固定時(shí)間控制方法中的奇異值問題,并且保證了控制輸入的值和導(dǎo)數(shù)在切換處連續(xù)。
3)提出了一種新的固定時(shí)間穩(wěn)定的補(bǔ)償系統(tǒng),用來補(bǔ)償迎角虛擬控制器飽和系統(tǒng)不確定性給控制性能帶來的不利影響。相比于文獻(xiàn)[21],本文方法可以將補(bǔ)償信號(hào)由指數(shù)穩(wěn)定提高到固定時(shí)間穩(wěn)定。
1 高超聲速飛行器動(dòng)力學(xué)模型及預(yù)備知識(shí)
1.1 飛行器動(dòng)力學(xué)模型
考慮到超燃沖壓發(fā)動(dòng)機(jī)對(duì)飛行姿態(tài)異常敏感和為了節(jié)省燃料,實(shí)際飛行中HFV應(yīng)盡量避免橫向機(jī)動(dòng),HFV的縱向動(dòng)力學(xué)模型可表示為[14]:
(1)
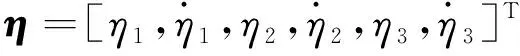
(2)
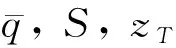
(3)
1.2 模型分解
本文采用反步法設(shè)計(jì)控制器,為了便于控制器設(shè)計(jì),假設(shè)sinγ≈γ, cosγ≈1[16]。考慮外部擾動(dòng)和氣動(dòng)參數(shù)攝動(dòng),將式(1)~(3)分解為速度子系統(tǒng)和高度子系統(tǒng),分別表示為:
(4)
(5)
式中:
(6)
式中:F=[FV,Fγ,Fα,FQ]T受氣動(dòng)參數(shù)攝動(dòng)和不可控彈性狀態(tài)影響,為系統(tǒng)的不確定項(xiàng);gV和gQ等于標(biāo)稱氣動(dòng)參數(shù)計(jì)算得到的值;d=[dV,dh,dγ,dα,dQ]T為未知的外界擾動(dòng)。
假設(shè)1[24].存在未知但有界的正函數(shù)FiM,diM,i∈{V,h,γ,α,Q}使得|Fi|≤FiM, |di|≤diM。
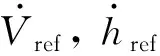
1.3 預(yù)備知識(shí)
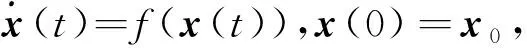
V(x)≤-aVp(x)-bVq(x)+η
(7)
那么稱系統(tǒng)的軌跡是實(shí)用固定時(shí)間穩(wěn)定的,并且穩(wěn)定時(shí)間Ts可以估計(jì)為:
(8)
式中:0<φ<1,系統(tǒng)的解將收斂至如下緊集內(nèi):
(9)
引理2[27].對(duì)于任意a≥0,b>0,c>0,下列不等式成立:
(10)
引理3[27].對(duì)于任意a>0,b≤a,c>1,下列不等式成立:
(a-b)c≥bc-ac
(11)
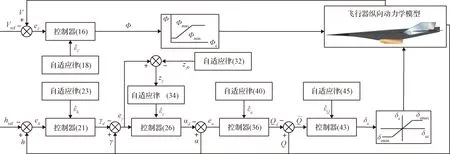
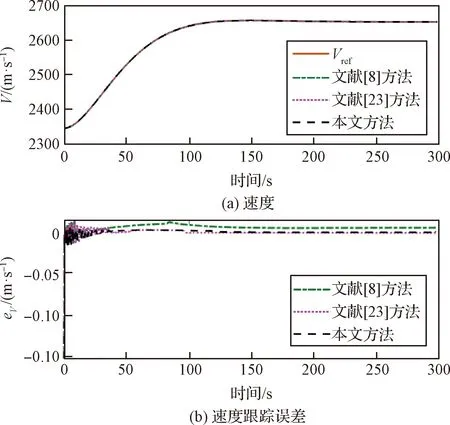
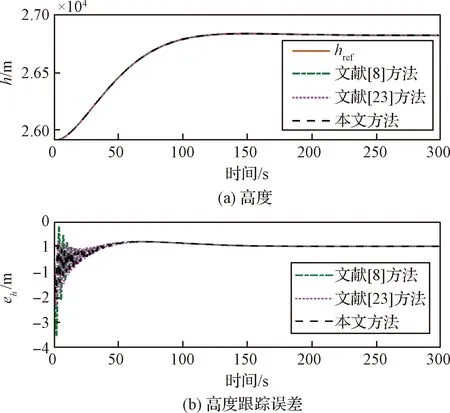
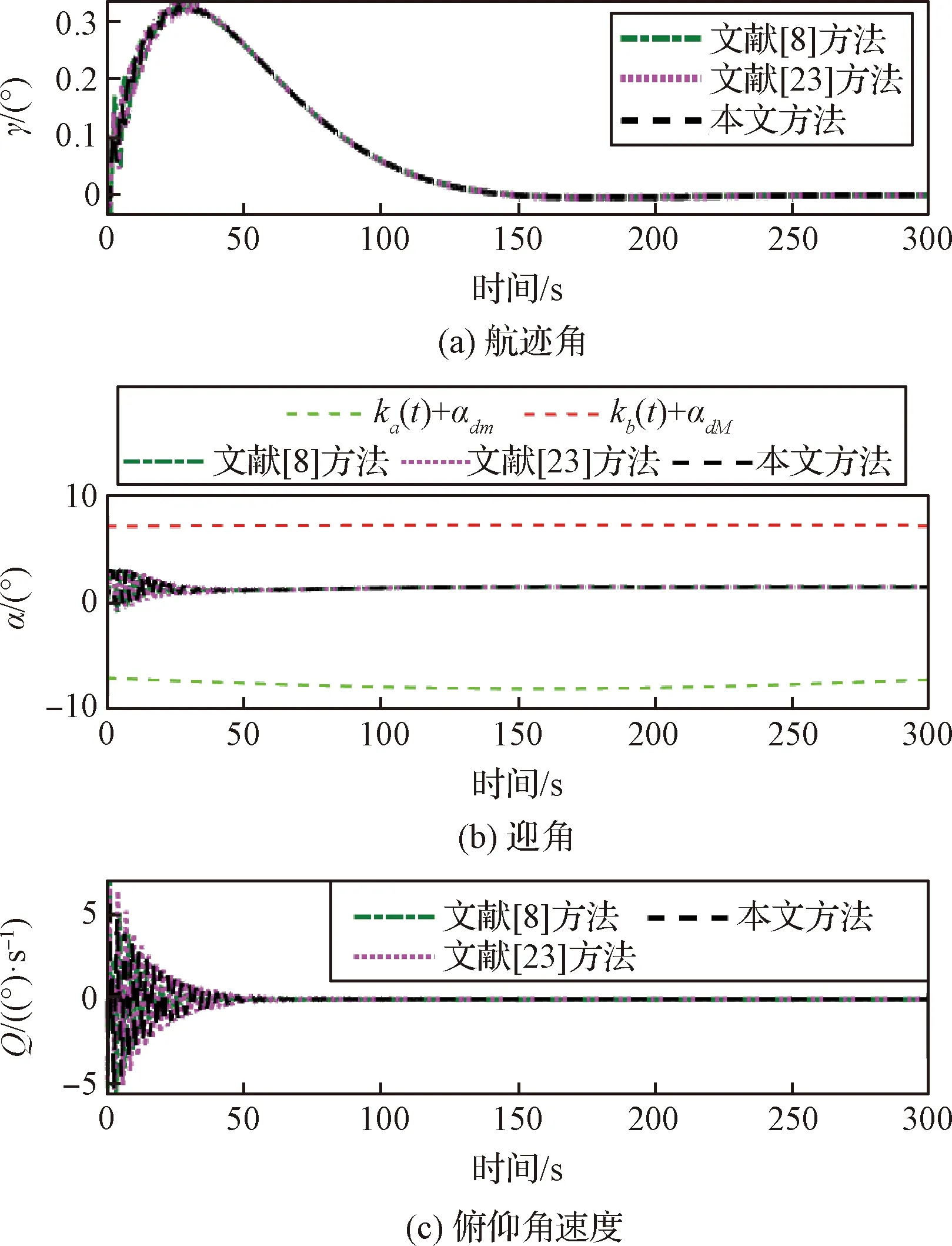
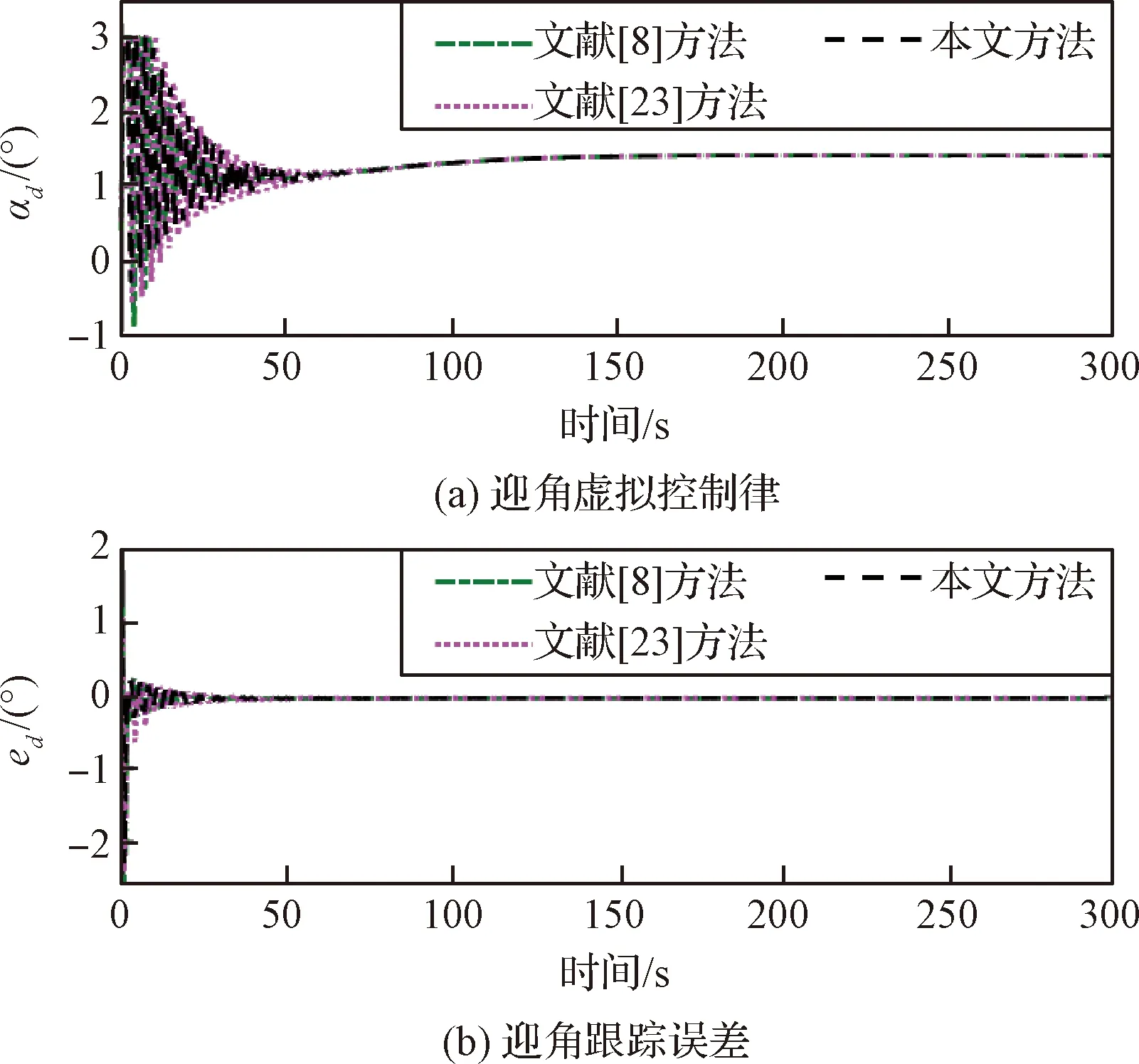
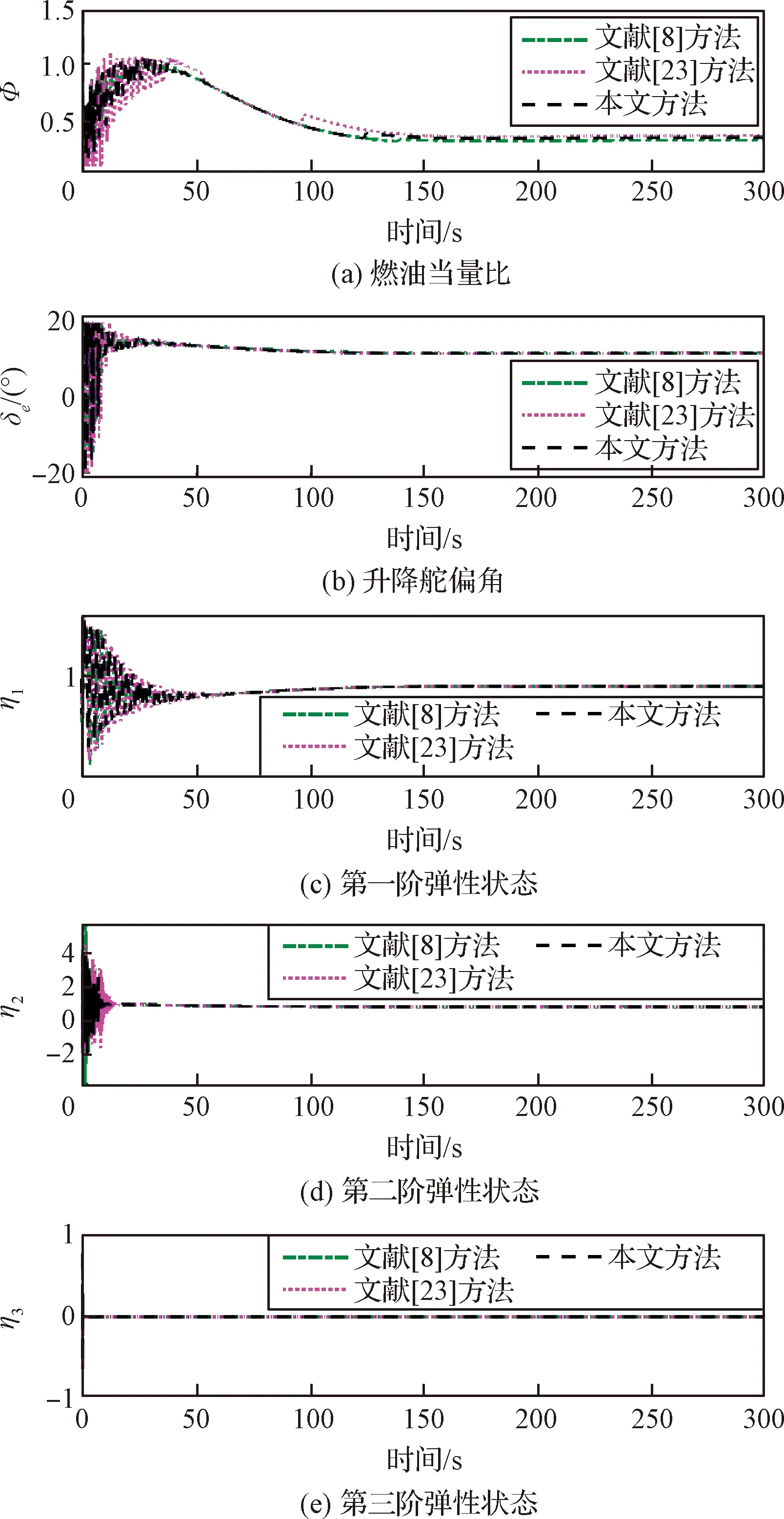
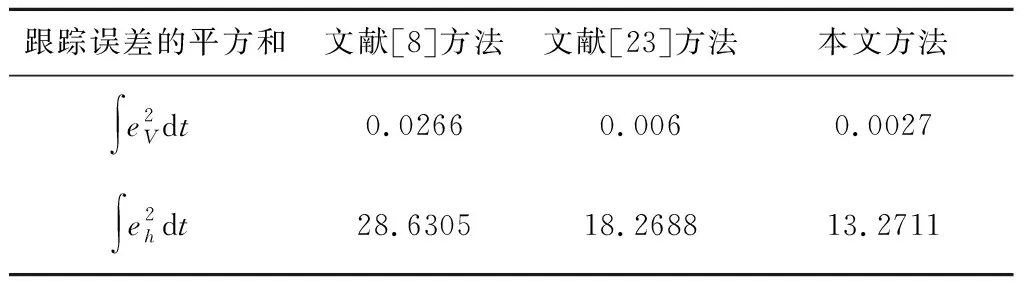
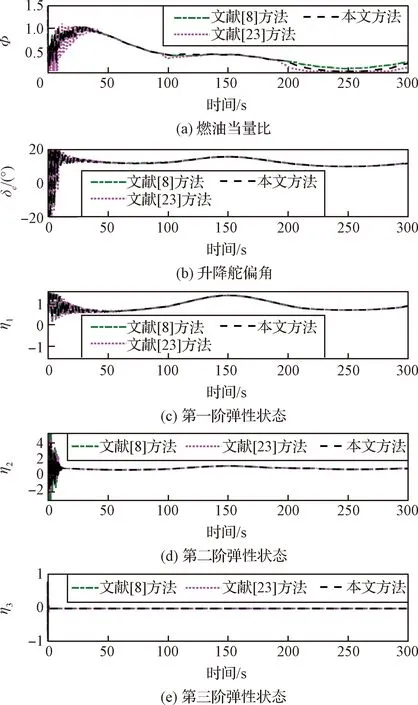
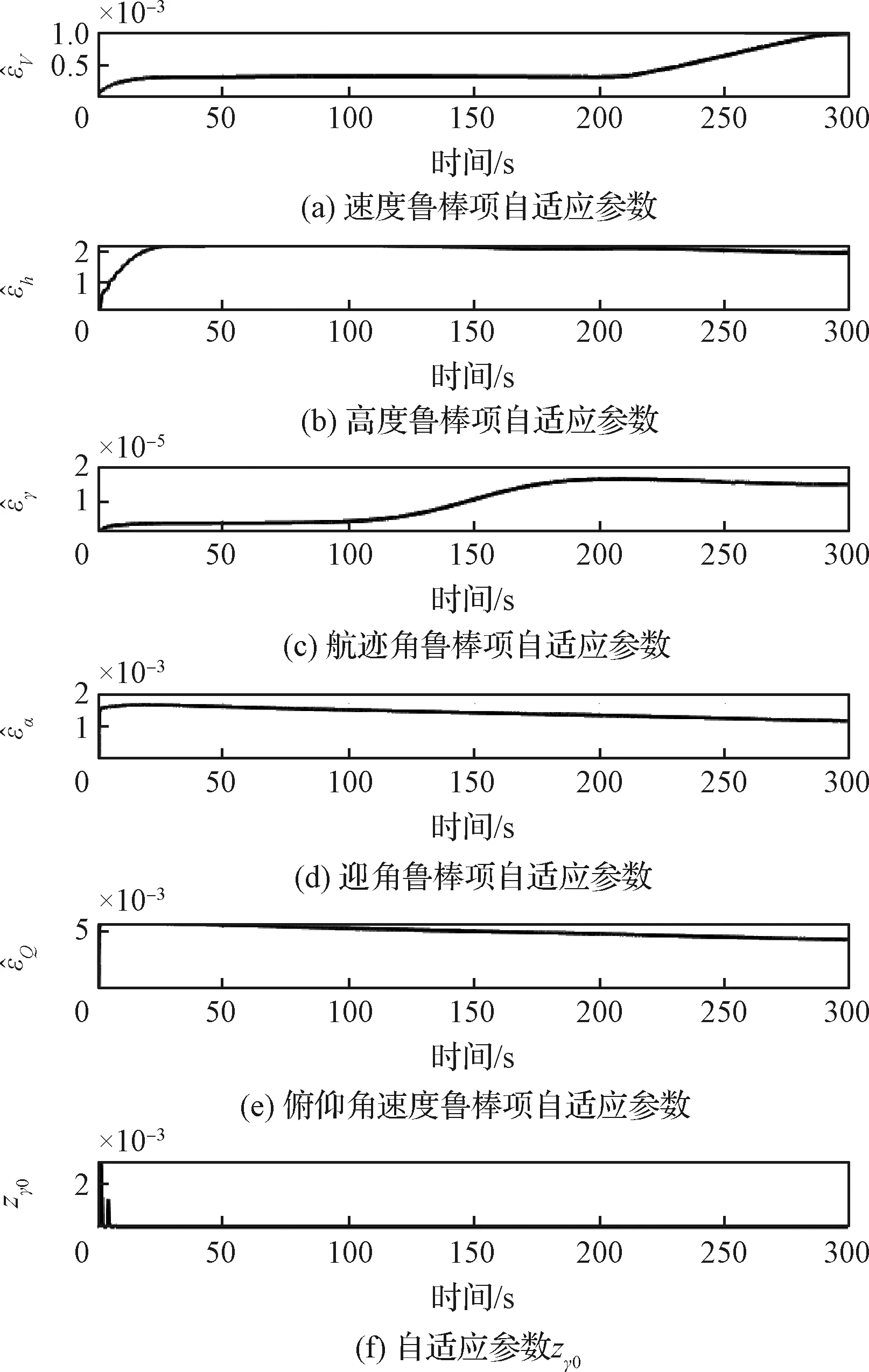
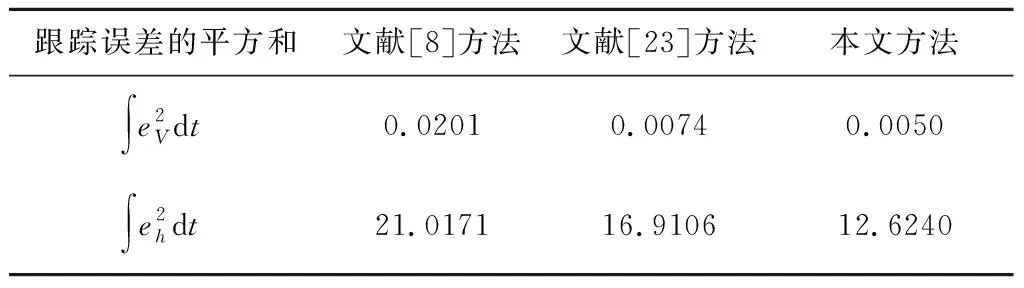
引理4[28]:對(duì)于任意k>0,如果存在常數(shù)e滿足|e| (12) (13) 定義速度跟蹤誤差為: eV=V-Vref (14) 式中:Vref為速度參考指令。結(jié)合式(4)和式(14),eV的導(dǎo)數(shù)為: (15) (16) 式中:p>1,kV1,kV2,kV3,σV為正的設(shè)計(jì)參數(shù)。sg(·q)=sgn(·)|·|q, sgn(·)為符號(hào)函數(shù)。切換函數(shù)?V被設(shè)計(jì)為: (17) 式中,0 設(shè)計(jì)自適應(yīng)律為: (18) 式中:lV1,lV2,lV3為正的設(shè)計(jì)參數(shù)。 1) 定義高度跟蹤誤差為: eh=h-href (19) 式中:href為速度參考指令。結(jié)合式(5)和式(19),eh的導(dǎo)數(shù)為: (20) (21) 式中:kh1,kh2,kh3,σh為正的設(shè)計(jì)參數(shù)。切換項(xiàng)?h設(shè)計(jì)為: (22) 式中:τh為正的設(shè)計(jì)參數(shù)。 設(shè)計(jì)自適應(yīng)律為: (23) 式中:lh1,lh2,lh3為正的設(shè)計(jì)參數(shù)。 2) 定義航跡角跟蹤誤差為: eγ=γ-γd (24) 結(jié)合式(5)和式(24),eγ的導(dǎo)數(shù)為: (25) (26) 式中:kγ1,kγ2,kγ3,σγ為正的設(shè)計(jì)參數(shù)。切換項(xiàng)?γ設(shè)計(jì)為: (27) 式中:τγ為正的設(shè)計(jì)參數(shù)。 為了滿足迎角限制,令αd通過如下飽和函數(shù): (28) 式中:αdM和αdm分別為αd的設(shè)計(jì)上下界。 定義迎角跟蹤誤差為: eα=α-αds (29) bα=αds-αd (30) 結(jié)合式(5)、式(29)和式(30),eγ的導(dǎo)數(shù)為: (31) 為了補(bǔ)償虛擬控制器飽和帶來的不利影響,定義zγ=eγ-zγ0。設(shè)計(jì)zγ0的自適應(yīng)律為: (32) zγ的時(shí)間導(dǎo)數(shù)為: (33) 設(shè)計(jì)自適應(yīng)律為: (34) 式中:lγ1,lγ2,lγ3為正的設(shè)計(jì)參數(shù)。 3) 由式(29)可得eα的導(dǎo)數(shù)為: (35) (36) 式中:kα1,kα2,kα3,σα為正的設(shè)計(jì)參數(shù)。切換項(xiàng)?α設(shè)計(jì)為: (37) 式中:τα為正的設(shè)計(jì)參數(shù)。 (38) 式中:οα為正的設(shè)計(jì)參數(shù)。 非對(duì)稱時(shí)變函數(shù)k(t)為: (39) 設(shè)計(jì)自適應(yīng)律為: (40) 式中:lα1,lα2,lα3為正的設(shè)計(jì)參數(shù)。 4) 定義俯仰角速度跟蹤誤差為: eQ=Q-Qd (41) 結(jié)合式(4)和式(41),eQ的導(dǎo)數(shù)為: (42) (43) 式中:kQ1,kQ2,kQ3,σQ為正的設(shè)計(jì)參數(shù)。切換項(xiàng)?Q設(shè)計(jì)為: (44) 式中:τQ為正的設(shè)計(jì)參數(shù)。 設(shè)計(jì)自適應(yīng)律為: (45) 式中:lQ1,lQ2,lQ3為正的設(shè)計(jì)參數(shù)。 本文設(shè)計(jì)的迎角受限控制器框圖如圖1所示。 圖1 迎角受限控制器設(shè)計(jì)框圖Fig.1 The design block diagram of the controller with AOA constraint 定理 1.考慮HFV動(dòng)力學(xué)系統(tǒng)(4)~(5),如果假設(shè)1~2成立且迎角初始跟蹤誤差滿足ka(0) 證.選擇如下Lyapunov函數(shù): L=LV+Lh+Lγ+Lα+LQ (46) 式中: (47) (48) (49) 對(duì)式(47)求導(dǎo)并代入式(15),(18),(20),(23),(25),(42),(45),可得: (50) 將式(16),(21),(43)代入式(50)得: (51) 根據(jù)楊氏不等式可得: (52) (53) 根據(jù)引理2~3可得: (54) (55) 根據(jù)引理5可得: (56) 將式(52)~(56)代入式(51)中,可得: (57) 對(duì)式(48)求導(dǎo)并代入式(32)~(34),可得: (58) 由楊氏不等式得: (59) (60) 結(jié)合式(53)~(55)和式(59)~(60),可將式(58)推導(dǎo)為: (61) 對(duì)式(49)求導(dǎo)并代入式(35)和式(40),可得: (62) 將式(36)代入式(62)并利用引理5,可得: (63) 由式(38)可得: (64) 根據(jù)楊氏不等式可得: (65) 根據(jù)式(46),(57),(61)和(65),可得: (66) 根據(jù)式(17),(22),(27),(37),(44)中?·的設(shè)計(jì),式(66)可分為以下兩種情形討論。 1) 當(dāng)|e·|>τ·時(shí),式(66)可寫為: (67) 式(67)可寫為如下形式: (68) 式中: 2) 當(dāng)|e·|≤τ·時(shí),式(69)可寫為: (69) 式(69)可寫為如下形式: (70) (71) 式中:Vref(s)和href(s)為濾波器的輸入;Vc(s)和hc(s)為濾波器的輸出。 表1 高超聲速飛行器的初始狀態(tài)Table 1 Initial states of HFV 為了說明本文所提的考慮非對(duì)稱時(shí)變迎角限制固定時(shí)間跟蹤控制器的有效性,將本文方法與文獻(xiàn)[8]中的考慮對(duì)稱迎角限制的跟蹤控制器以及文獻(xiàn)[23]中的考慮非對(duì)稱時(shí)變迎角限制的跟蹤控制器進(jìn)行對(duì)比分析。 情形1:假設(shè)氣動(dòng)參數(shù)等于標(biāo)稱值,且無外界擾動(dòng),且存在初始誤差eV(0)=-0.1524 m/s,eh(0)=-0.1524 m。 情形1下的速度和速度跟蹤誤差如圖2所示,高度和高度跟蹤誤差如圖3所示。可以看出,在標(biāo)稱參數(shù)情形下,采用本文方法產(chǎn)生的速度跟蹤誤差的超調(diào)量和高度跟蹤誤差的超調(diào)量要小于文獻(xiàn)[8]和文獻(xiàn)[23]方法產(chǎn)生的超調(diào)。圖4為航跡角、迎角和俯仰角速度,采用三種方法的迎角均能保持在預(yù)設(shè)限制內(nèi)。圖5為迎角虛擬控制律和迎角跟蹤誤差,采用三種迎角受限跟蹤控制方法都能將迎角虛擬控制律和跟蹤誤差限制在設(shè)定范圍內(nèi)。燃油當(dāng)量比、升降舵偏角和彈性狀態(tài)如圖6所示,可見采用本文方法的控制輸入和彈性狀態(tài)很快穩(wěn)定。從圖7可外界以看出,本文方法的魯棒項(xiàng)自適應(yīng)參數(shù)及自適應(yīng)參數(shù)zγ0是有界的。為了更加明顯地比較三種方法的控制性能,將三種方法的速度跟蹤誤差的平方和以及高度跟蹤誤差的平方和列于表2中。可見,采用本文方法得到的速度跟蹤誤差平方和以及高度跟蹤誤差平方和都小于文獻(xiàn)[8]和文獻(xiàn)[23]方法得到的速度跟蹤誤差平方和以及高度跟蹤誤差平方和。因此,本文方法具有更好的控制性能。 圖2 速度和速度跟蹤誤差Fig.2 The velocity and tracking errors of velocity 圖3 高度和高度跟蹤誤差Fig.3 The altitude and tracking errors of altitude 圖4 航跡角、迎角和俯仰角速度Fig.4 The flight path angle, AOA and pitch rate 圖5 迎角虛擬控制律和迎角跟蹤誤差Fig.5 The virtual law of AOA and tracking errors of AOA 圖6 燃油當(dāng)量比、升降舵偏角和彈性狀態(tài)Fig.6 The Fuel equivalent ratio, elevator deflection angle and flexible states 圖7 魯棒項(xiàng)自適應(yīng)參數(shù)及自適應(yīng)參數(shù)zγ0Fig.7 The adaptive parameters of robust term and the adaptive parameters zγ0 表2 情形1的跟蹤誤差平方和Table 2 The squares sum of tracking errors for Case 1 情形2:假設(shè)初始誤差與情形1相同,考慮未知擾動(dòng)dV=sin(0.1πt),dγ=dα=0.001sin(0.01πt),dQ=0.01sin(0.01πt),以及氣動(dòng)參數(shù)攝動(dòng): (72) 式中:Ci,i∈{L,D,M,T}表示考慮不確定性的參數(shù)值,Ci0表示標(biāo)稱的參數(shù)值。 情形2下的速度和速度跟蹤誤差如圖8所示,高度和高度跟蹤誤差如圖9所示。可見本文方法不僅能使速度和高度更快地跟蹤上參考指令,而且在受到外界擾動(dòng)影響時(shí),能使跟蹤誤差的波動(dòng)更小。航跡角、迎角和俯仰角速度如圖10所示,采用三種控制方法皆能保證迎角不超出預(yù)設(shè)限制。圖11為迎角虛擬控制律和迎角跟蹤誤差,采用三種控制方法都能將迎角虛擬控制律和跟蹤誤差限制在設(shè)定范圍內(nèi)。圖12為燃油當(dāng)量比、升降舵偏角和彈性狀態(tài)。圖13顯示本文方法的魯棒項(xiàng)自適應(yīng)參數(shù)及自適應(yīng)參數(shù)zγ0是有界的。情形2的速度跟蹤誤差的平方和以及高度跟蹤誤差的平方和如表3所示,在存在參數(shù)攝動(dòng)和外界擾動(dòng)的情形下,本文方法仍具有更加優(yōu)越的控制性能。 圖8 速度和速度跟蹤誤差Fig.8 The velocity and tracking errors of velocity 圖9 高度和高度跟蹤誤差Fig.9 The altitude and tracking errors of altitude 圖10 航跡角、迎角和俯仰角速度Fig.10 The flight path angle, AOA and pitch rate 圖11 迎角虛擬控制律和迎角跟蹤誤差Fig.11 The virtual law of AOA and tracking errors of AOA 圖12 燃油當(dāng)量比、升降舵偏角和彈性狀態(tài)Fig.12 The fuel equivalent ratio, elevator deflection angle and flexible states 圖13 魯棒項(xiàng)自適應(yīng)參數(shù)及自適應(yīng)參數(shù)zγ0Fig.13 The adaptive parameters of robust term and the adaptive parameters zγ0 表3 情形2的跟蹤誤差平方和Table 3 The squares sum of tracking errors for case 2 本文考慮非對(duì)稱時(shí)變迎角限制、氣動(dòng)參數(shù)不確定性以及外界擾動(dòng)的影響,開展了高超聲速飛行器的固定時(shí)間非奇異跟蹤控制研究。通過理論分析和仿真驗(yàn)證,有如下結(jié)論成立: 1) 設(shè)計(jì)了固定時(shí)間非奇異魯棒跟蹤控制器,保證系統(tǒng)的跟蹤誤差和估計(jì)誤差在固定時(shí)間內(nèi)收斂,且能避免奇異點(diǎn)問題。 2) 所設(shè)計(jì)的控制器能夠保證高超聲速飛行器的迎角始終不超出預(yù)設(shè)的非對(duì)稱時(shí)變限制。 3) 相比于跟蹤誤差按指數(shù)收斂的迎角受限控制器,所設(shè)計(jì)控制器具有更好的控制性能。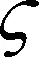
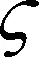
2 固定時(shí)間自適應(yīng)控制器設(shè)計(jì)
2.1 速度控制器
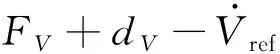
2.2 高度控制器
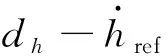
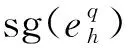
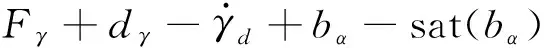
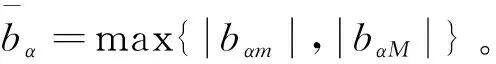
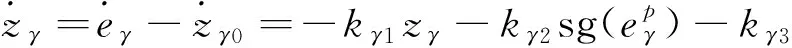
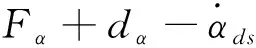
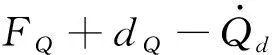
3 穩(wěn)定性分析
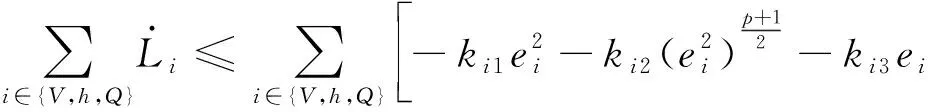
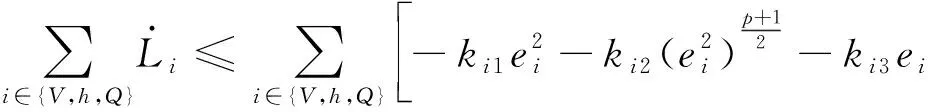
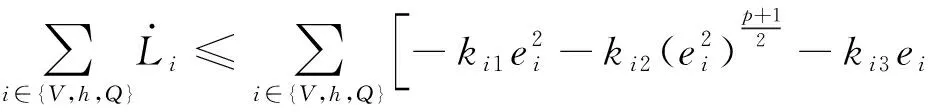
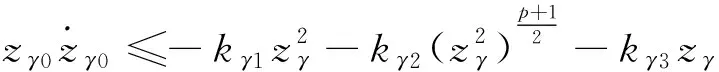
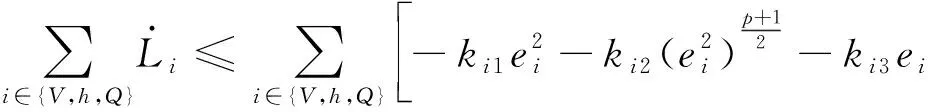

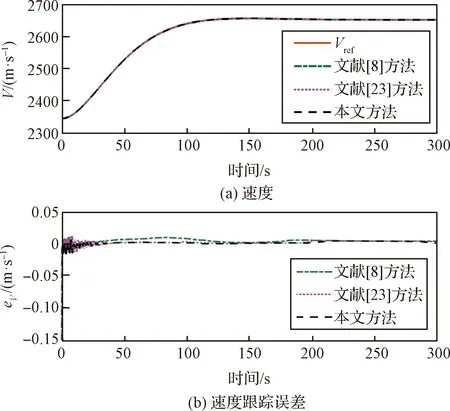
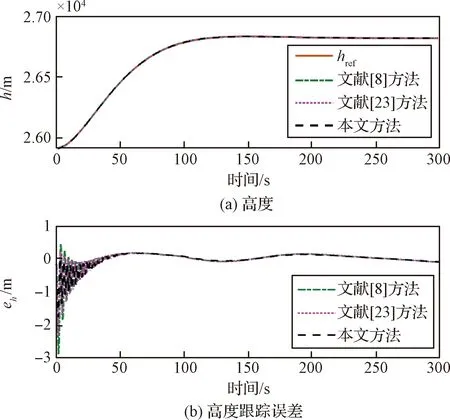
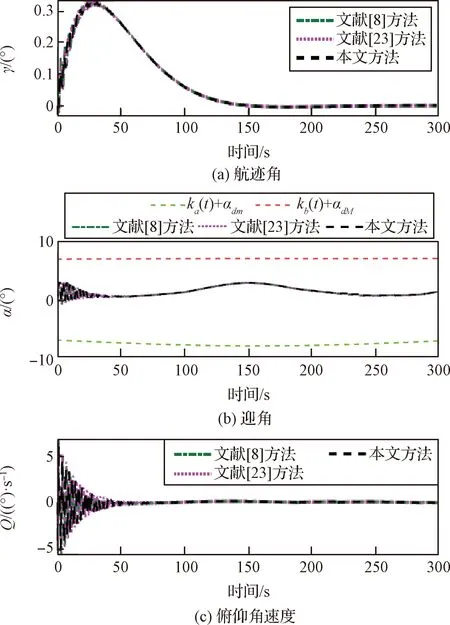
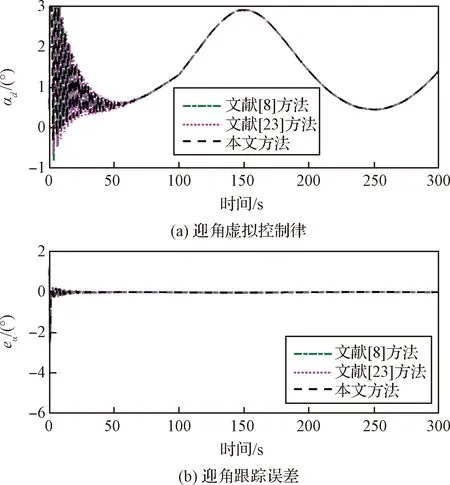
4 仿真校驗(yàn)



5 結(jié) 論

