巴特沃斯低通濾波器的設計與仿真分析
楊輝


摘要:巴特沃斯濾波器具有通頻帶內的頻率響應曲線最大限度平坦、沒有紋波、而在阻頻帶則逐漸下降為零的優點。本文從巴特沃斯濾波器的傳遞函數著手,針對特定設計參數通過雙線性變換完成了數字濾波器的設計,最后通過仿真分析,展示了巴特沃斯濾波器在幅值衰減與相位滯后的特點,為工程技術人員在濾波器的選擇與設計上提供參考。
關鍵詞:巴特沃斯濾波器;傳遞函數;雙線性變換
0引言
巴特沃斯濾波器(Butterworth Filter)也被稱作最大平坦濾波器。其特點是在通頻帶內,其頻率響應曲線最大限度平坦、單調遞減無波紋產生;而在阻頻帶內,其頻率響應曲線逐漸下降為零。這些優點使其在信號處理領域有著廣泛的應用。對于濾波器的性能一般考慮其幅頻特性,但對于更深層次的信號處理應用方面,濾波器的相頻特性也是其重要特性之一。尤其是在多點激勵、載荷建立以及傳遞路徑識別等方面問題的研究中具有重要作用。
1巴特沃斯濾波器傳遞函數分析
連續時間巴特沃斯低通濾波器可用式(1)表示。
式中:B(jω)為連續時間巴特沃斯傳遞函數,ω為頻率,ωC 為濾波器截止頻率,N 為階數,該濾波器 Bode 圖如圖1所示。
將式(1)轉換為 Laplace 域分析,即令 s=jω,可得到式(2)。
圖1巴特沃斯濾波器Bode圖
求解式(2)的極點,可得式(3)。
對極點作歸一化處理,即令:
作歸一化巴特沃斯濾波器的拉普拉斯域平面,可以得到2N個以虛軸Im對稱的極點,以 N=3為例其極點分布如圖2所示,所有極點都均分在以原點為中心的單位圓上。
為形成因果穩定系統,取左半平面極點構建式(5)的傳遞函數。
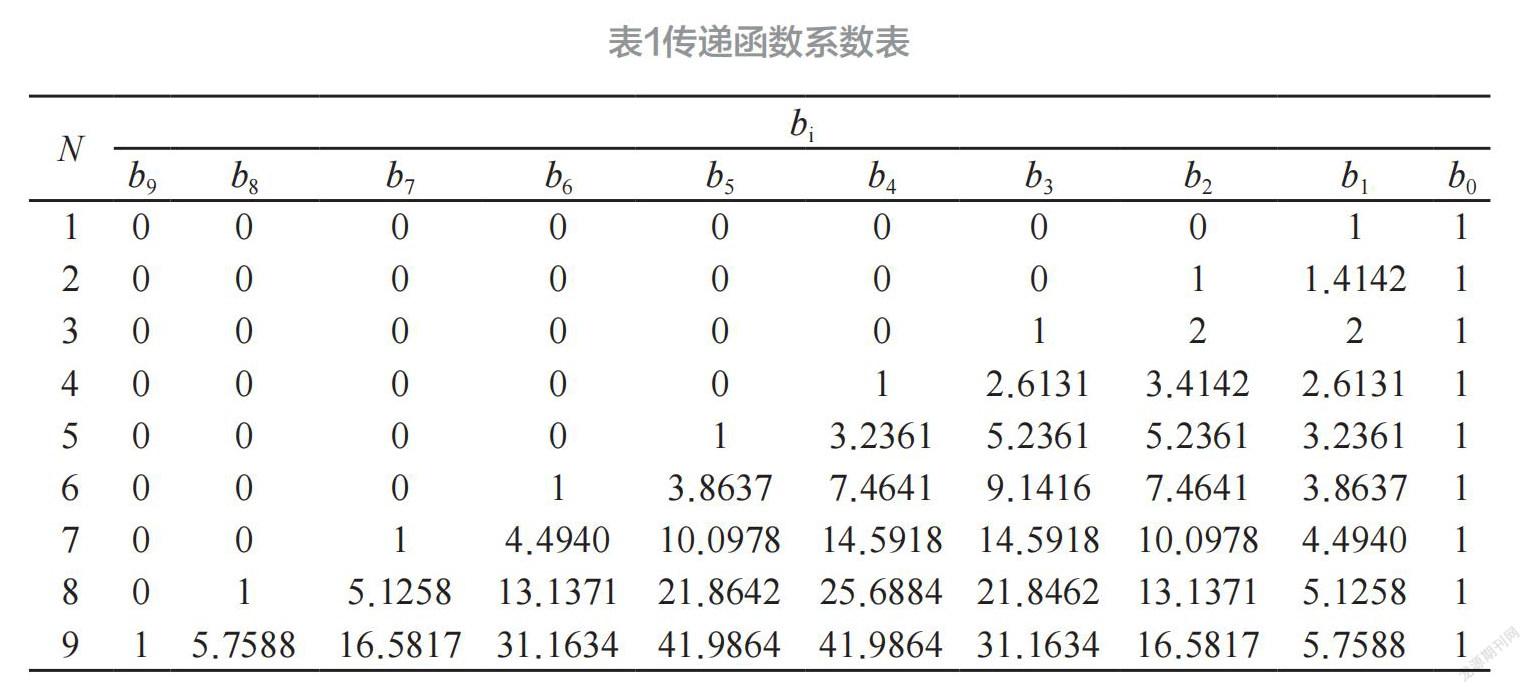
其中多項式系數 bi 可構為建歸一化 N 階巴特沃斯濾波器的傳遞函數系數,不同階數系數如表1所示。
對應不同階數 N,繪制歸一化巴特沃斯濾波器Bode 圖如圖3所示。
2數字濾波器設計實例
現以表2所述濾波器性能參數,實例設計巴特沃斯型數字濾波器。
針對通帶截止頻率與阻帶截止頻率設計要求,建立式(6)與(7)的濾波器設計約束條件。
通過約束條件,可通過式(8)得到理論設計階數。
由于階數需為整數,將理論階數 N*向高階取整以得到 N,并代入式(9),即可得到截止頻率ωC。
經計算,N=4,ωC=5.275 kHz,通過歸一化濾波器系數,即可表得到濾波器的傳遞函數為式(10)。
采用雙線性變換法,即通過式(11)完成 s 域到 z域的映射。由此即可得到在采樣頻率下的數字濾波器傳遞函數。
3 濾波器的仿真分析
仿真過程中,通過構建兩路不同頻率正弦波信號x1 和 x2 進行疊加作為輸入,其中 x1 為 300 Hz,x2 為15 kHz。按圖 4 所示原理圖,將疊加信號通過采樣器采樣后輸入數字濾波器,通過示波器分別顯示原始疊加信號、低頻信號與濾波信號的波形。
通過圖 5 的波形分析可以看出,該濾波器可以很好的將高頻信號濾除,濾波信號的波形基本能夠還原輸入的低頻信號。只是在幅值上有 0.028% 的衰減,相位上存在 127.433 ?s 的延遲。
4 結束語
本文從巴特沃斯濾波器的設計原理著手,通過極點分析推導了巴特沃斯系數表的構建方法,并分析了設計階數對濾波器的幅頻特性與相頻特性所產生的影響。通過結合實例指標參數要求,使用雙線性變換法完成了巴特沃斯型數字濾波器的設計。最后通過仿真分析,驗證了該數字濾波器的濾波效果,結果表明在通頻段信號的幅值有微弱的降低,相位有少量滯后,但總體還原程度較高,效果理想。
參考文獻:
[1][美]ALAN V O,等.信號與系統[M].3版.劉樹棠,譯.北京:電子工業出版社,2013.
[2]龔作豪,沈君鳳.巴特沃斯低通濾波器的仿真設計[J].信息通信, 2014(139):40-41.
[3]仲帥.基于改進粒子群算法的數字濾波器設計及應用[D].長春:吉林大學,2016.

