巧用實數定方案

文／王云峰

實數在生活中至關重要，我們時時刻刻都能用到它。下面，我們一起來看看生活中的實數問題。

例為了增加小區的綠化面積，幸福公園準備修建一塊面積為121πm2的草坪，草坪周圍用籬笆圍繞。現從對稱美的角度考慮設計了甲、乙兩種方案。

甲方案：建成正方形；

乙方案：建成圓形。

（1）如果從節省籬笆費用的角度考慮，你會選擇哪種方案呢？請說明理由。

（2）對方案進行審批時發現，修如此大的草坪目的是親近自然，若按甲、乙兩種方案就達不到目的，因此建議用如圖1 所示的設計方案：建成正方形，正方形里修三條小路，三條小路的寬度相同，這樣草坪的實際面積就減少了21πm2，求此方案中小路的寬度。

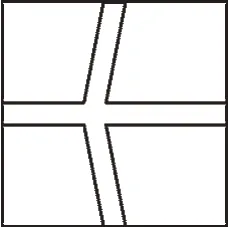
圖1

【分析】（1）從節省籬笆費用的角度考慮，就是比較正方形的周長與圓的周長的大小，選擇其中周長較小的即可；（2）將與正方形的邊不平行的小路進行平移，再根據修三條小路后草坪的面積列方程求解即可。

解：（1）選擇乙方案。

理由如下：設甲方案中正方形的邊長為xm。根據題意得x2=121π。

∴x=

∴正方形的周長為4x=44

設乙方案中圓的半徑為rm，根據題意得πr2=121π。

∴r=11。∴圓的周長為2πr=22π（m）。

∴從節省籬笆費用的角度考慮，我會選擇乙方案。

（2）根據題意可對小路進行如圖2 所示的平移。設小路的寬度為ym。根據題意，得

圖2

比較正無理數的大小，我們可采用平方法，即將無理數進行平方，平方的結果較大的無理數也較大。