水下垂直樁柱結構局部沖刷研究與進展

李健華，周 川，王 俊，潘冬冬，孫忠濱

(1.中國能源建設集團廣東省電力設計研究院有限公司,廣州 510663;2.廣東科諾勘測工程有限公司,廣州 510663;3.南京水利科學研究院,南京 210029)

海上風電是清潔能源以及可再生能源的重要發展方向之一，兼具良好的規模化開發條件和商業化發展前景，因此在世界范圍內得到了廣泛的關注。與陸地風能資源相比，海上風能資源具有風速大，風垂直切變更小，年利用時間長等明顯優勢，因此近年來我國的海上風電事業得到了蓬勃發展。風機基礎是保障風機安全運行的重要設施，占整個風電場建造成本的20%～30%。單樁基礎具有結構形式簡單、施工工藝成熟、建造成本較低等特點，因此廣泛應用于海上風電工程。原本處于動態平衡的海床，由于單樁基礎的安裝，勢必會改變當地的水動力條件，使得維持動態平衡的外部條件被打破，其直接后果是導致結構物附近的泥沙發生局部沖刷。局部沖刷會使得樁基基礎的承載力下降，橫向受力不均勻，最終會導致樁基基礎發生在位失穩，嚴重威脅風機的安全運營。此外，風機基礎的局部沖刷涉及到復雜的流體-結構-海床強非線性相互作用，其中蘊含著豐富的物理現象。因此，有關風機基礎的局部沖刷研究工作具有重要的工程應用價值和科學研究意義。本文從風機基礎局部沖刷的沖刷機理、物理模型試驗、數值模擬和理論分析、現場觀測等方面對已有的研究工作進行總結和分析，在此基礎上，對未來研究工作的開展給出建議。

1 沖刷機理研究

海上單樁風機基礎通常為圓柱形結構。因此，國內外的眾多學者將其簡化為水下直立圓柱，進而對其局部沖刷問題開展研究工作。當流體流經圓柱結構時，由于結構的存在，導致其周圍的流動結構發生深刻變化，具體包括圓柱前方的下降水流、前緣馬蹄渦結構、后方尾渦脫落以及圓柱兩側的流線收縮，相關的流動結構如圖1所示，流動結構的改變對圓柱的局部沖刷有著重要的影響作用。

圖1 單樁基礎周圍流動結構[1]Fig.1 Schematic diagram of flow structure around a vertical pile[1]

馬蹄渦是誘發水下垂直圓柱發生局部沖刷的關鍵因素，眾多學者對其開展大量的研究工作。由于圓柱的存在，其上游會產生負壓梯度，從而使來流邊界層發生流動分離，分離的邊界層會在圓柱的前緣形成馬蹄渦系結構[1]。SCHWIND[2]和BAKER[3]在風洞試驗中通過煙霧可視化技術、DARGAHI[4]在水槽試驗中使用氫氣泡可視化技術證明了馬蹄渦系結構的存在。HJORTH[5]和BAKER[3]通過在水槽試驗中測量流速剖面，分析獲得了馬蹄渦結構對海床剪切應力τ分布的影響作用。相關的研究結果表明，馬蹄渦影響下的海床剪切應力值相比遠場情況增加了5～11倍[5]，海床剪切應力的放大是結構發生局部沖刷的決定性因素。HJORTH[5]和BAKER[3]的研究結果證明了馬蹄渦是影響圓柱局部沖刷的重要因素。BAKER[3]還研究了影響馬蹄渦強度的因素，包括來流邊界層厚度δ、雷諾數Re、樁柱橫截面形狀、淹沒高度等，其中，Re數的定義為Re=UD/υ，U為來流流速、D為結構特征長度(對于圓柱結構，特征長度為其直徑)、υ為流體的運動粘性系數。

圓柱兩側的流線收縮以及后方脫落的卡門渦街也是影響局部沖刷的重要因素。SUMER和FREDS?E[1]通過對圓柱兩側海床剪切應力的分析，解釋了流線收縮對局部沖刷的影響作用。尾渦是由圓柱兩側表面的邊界層分離所引起的，主要影響因素為雷諾數Re和截面形狀。SUMER和FREDS?E[6]對圓柱后方尾渦脫落開展了系統研究工作，闡明了發生渦脫落的物理機制，分析了雷諾數Re、表面粗糙度、截面形狀、來流湍流度等因素對渦脫落的影響。

上述的研究工作表明，馬蹄渦的形成和圓柱兩側的流線收縮，使得圓柱近底周圍的床面剪切應力增大，導致輸沙率增加，進而在結構物四周形成倒錐形的局部沖坑。在下降水流的淘刷作用下，沖刷坑進一步擴展；同時，馬蹄渦強度逐漸增強并向沖坑內移動，與后方尾渦共同作用將沖坑內泥沙輸運到下游。

2 物理模型實驗研究

根據來流條件所對應希爾茲參數θ與泥沙臨界希爾茲參數θcr的關系，可將局部沖刷分為清水沖刷(θ>θcr)和動床沖刷(θ>θcr)。眾多學者對這兩種條件下的圓柱局部沖刷問題開展了大量物理模型試驗研究工作，主要研究局部沖刷的發展規律、沖刷時間尺度T、平衡沖刷深度S0對相關影響因素的依賴關系，并建立了相應的經驗預報模型。

FREDS?E和SUMER等[7]基于松散均勻沙試驗，建立了均勻流條件下，圓柱局部沖刷深度隨時間變化的經驗公式

(1)

式中：T為沖刷時間尺度；t為時間。WHITEHOUSE[8]對上述公式進行了改進，通過在公式(1)中引入了冪指數項i，使得對沖刷的發展過程及平衡沖刷深度的預報更加準確，其公式為

(2)

BRIAUD等[9]基于粘性土沖刷試驗，同時引入沖刷擴展速率的概念，提出了沖刷深度隨時間變化的公式

(3)

式中：V為在沖刷初始階段的擴展速率，BRIAUD等[9]同時給出了平衡沖刷深度S0的表達式，該表達式唯一依賴于Re數，形式為S0(mm) = 0.18Re0.635。

影響局部沖刷深度的因素較多，如泥沙級配、圓柱淹沒深度、截面形狀、泥沙粘性等，眾多學者針對上述影響因素開展了系統的研究工作。RAUDKIVI和ETTEMA[10]研究了清水沖刷條件下泥沙幾何均方差對平衡沖刷深度的影響作用，發現該物理量對局部沖刷有較大的影響。隨后，BAKER[11]通過實驗發現，在動床沖刷條件下，泥沙顆粒的幾何均方差對平衡沖刷深度的影響相對清水沖刷較弱。BAKER[12]開展了樁柱淹沒高度對平衡沖刷深度影響的研究工作。相關的結果表明，隨著樁柱高度的增大，馬蹄渦的強度會不斷增強，平衡沖刷深度也會隨之增大；當圓柱高度大于5D時，將不再對平衡沖刷深度產生影響。MELVILLE和SUTHERLAND[13]研究了水深對平衡沖刷深度的影響，并在水深與圓柱直徑比h/D<2.6時，引入了水深影響系數Kh=0.78(h/D)0.255，得出圓柱周圍可能發生的最大沖刷深度為2.4D。但在MELVILLE和CHIEW[14]后續的研究工作中提出，當水深較淺時，水深對沖刷平衡深度的影響需要開展進一步研究工作。MELVILLE和SUTHERLAND[13]根據ETTEMA[15]和CHIEW[16]的動床沖刷實驗數據，分析了泥沙中值粒徑d50對平衡沖刷深度的影響。當D/d50<50時，平衡沖刷深度隨泥沙中值粒徑的增大而增大；而當D/d50≥50，泥沙中值粒徑不再對沖刷平衡深度產生影響，ETTEMA[15]認為這是由于泥沙顆粒間孔隙率增大引起的水流能量耗散所導致的。SUMER和CHRISTIANSEN等[17]研究了截面形狀對平衡沖刷深度的影響，闡明了截面形狀影響馬蹄渦的強度，進而影響沖刷深度的物理機制。MELVILLE和SUTHERLAND[13]根據物理模型試驗結果，引入截面形狀系數，從而獲得了具有不同截面形狀立柱結構的局部沖刷平衡深度預測公式。LAURSEN[18]研究了矩形截面與來流角度對立柱沖刷深度的影響作用。BRIAUD[9]開展了垂直圓柱在粘性土條件下的局部沖刷實驗，其研究結果表明，粘性海床達到平衡沖刷深度所需的時間要遠大于松散均勻沙的條件，這也是國際上目前開展的為數不多的基于粘性土的物理模型試驗。于通順[19]通過開展復合筒型基礎在單向流作用下的物理沖刷實驗，獲得了結構基礎周邊的沖刷深度和沖刷平衡時間。研究發現，沖刷坑呈勺狀并且其分布范圍在基礎模型后方45°～90°的區域內。韓海騫[20]針對杭州灣跨海橋梁沖刷結果進行了系統地分析，通過研究給出了水流作用下的大直徑橋梁墩柱局部沖刷計算公式。李林普等[21]通過對水流作用下大直徑圓柱基底的局部沖刷進行研究，得到了適用于淺海砂質海床的最大沖深計算公式。研究結果表明，大直徑圓柱基底沖淤圖呈W型，最大沖深位于圓柱前方45°～90°的區域內。MELVILLE和SUTHERLAND[13]對于均勻流作用下具有不同截面形狀的水下垂直樁柱平衡沖刷深度開展研究工作，建立如式(4)所示的可考慮多種因素影響的平衡沖刷深度預報公式[13]

S0/D=KIKδKdKsKα

(4)

式中：KI、Kδ、Kd、Ks、Kα分別為與希爾茲數、水深、泥沙中值粒徑、截面形狀、來流攻角有關的參數。

此外，王汝凱[22]基于水槽試驗，總結了適用于波浪引起沖刷計算的公式。周益人和陳國平[23]對大直徑圓柱式結構物在不規則波作用下的局部沖刷進行實驗研究，給出了大直徑圓柱結構的最大沖刷深度計算公式。在波浪作用下的平衡沖刷深度預測方面，SUMER和FREDS?E[1]基于大量的實驗數據，得到了考慮波浪KC數影響條件下的垂直圓柱局部沖刷經驗預報公式

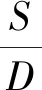
(5)

式中：KC數的定義為KC=UwT/D，其中Uw為波浪水質點運動速度的幅值，T為波浪周期。

黃瑩等[24]開展了海洋平臺樁基的沖刷機理研究，考慮了樁基、波流以及泥沙的相互作用，利用海床剪切應力、泥沙起動率以及輸沙率等參數判斷泥沙的運動狀態，得到樁基局部沖刷結果與SUMER和FREDS?E[25]較為一致。程永舟等[26]利用SUMER和FREDS?E[25]提出的沖深計算公式和Stokes二階波浪理論，提出了隨機波和水流共同作用的沖刷計算方法。研究發現，引起細顆粒泥沙運動的滲流力隨著波浪周期增大而增大。楊子希等[27]采用系列模型試驗方法，針對極細沙海床在波流共同作用下的樁基礎沖刷深度及防護措施效果展開研究，并將試驗結果與學者經驗公式計算結果進行比較。對于波流聯合作用下的平衡沖刷深度預測，SUMER和FREDS?E[1]提出以下經驗公式

(6)

式中：S0為根據式(4)計算得到的水流作用下平衡沖刷深度預測結果，A和B是與流動條件相關的參數。其中A=0.03+0.75Ucw2.6，B=6×exp(-4.7Ucw)，Ucw=U/(U+Uw)。

以上基于物理模型試驗，對影響圓柱局部沖刷的各項因素進行了總結分析，并給出了不同流動條件下的沖刷平衡深度經驗預報公式。需要說明的是，以上經驗公式基本都是在松散均勻沙物理試驗基礎上獲得的，難以考慮實際工程現場海域常見粘土的輸運特性，需要開展更加深入的研究工作，從而使得基于實驗室松散均勻沙所建立的經驗預報公式更加具有工程指導價值。

3 數值模擬和理論分析

如前文所述，圓柱前緣的馬蹄渦流動結構是影響其局部沖刷的關鍵因素，BRILEY和MCDONAL[28]、KWAK等[29]、DENG和PIQUET[30]、KOBAYASHI[31]等眾多學者開展了大量數值模擬研究工作，通過對流動結構的分析，系統地研究了馬蹄渦結構的生成和演化機制，為進一步研究圓柱局部沖刷的數值模擬奠定了重要基礎。方許聞等[32]在理想數值水槽中，將風電樁基作為陸域邊界直接模擬，通過等效阻力法和等阻水面積法對樁基進行概化，通過對這兩種概化方法的結果進行比較分析，表明在實際應用中需根據樁基的形式選取適合的概化方法。李紹武和楊航[33]利用FLOW-3D三維模擬軟件中大渦模擬紊流模型模塊以及泥沙沖刷模塊，對不同尺度圓柱周邊的局部沖刷進行系統模擬研究。計算結果表明，在不同圓柱直徑下，圓柱的迎水側、背水側以及對稱側的平衡沖刷深度始終保持著特定的比例關系。

在清水沖刷的數值模擬方面，OLSEN和MELAAEN[34]較早開展了圓柱局部沖刷的數值模擬研究工作。在其數值模型中，流體運動的控制方程為雷諾平均的Navier-Stokes方程，并采用k-ε模型進行湍流封閉，模型中同時考慮可懸移質輸沙和推移質輸沙，數值計算得到的沖坑幾何特征與試驗結果吻合較好，驗證了通過數值模擬進行圓柱局部沖刷研究的可行性。需要說明該項工作僅對沖刷的初始階段進行模擬，沖刷未達到平衡。在此基礎上，OLSEN和KJELLESVING[35]進一步對清水沖刷條件下圓柱局部沖刷的整個歷程開展數值模擬工作，模擬得到的平衡沖刷深度與經驗公式計算結果吻合良好。張博杰[36]基于OpenFOAM開源程序構建了三維水流模型，并利用海床切應力平衡方法給出了海洋結構物局部沖刷的數學模型。研究結果表明，利用三維水流-局部沖刷數學模型可以較好地模擬圓柱周圍粘性泥沙的沖刷過程，得到的最大沖深與物理模型試驗較為一致。趙雁飛[37]利用FLOW-3D流體程序構建了三維數值水池，針對波浪作用下風電基礎的受力情況和基礎局部沖刷情況開展系統研究。研究結果表明，利用FLOW-3D構建的三維數值水池可以準確地模擬風電基礎沖坑深度，并能較好地捕捉沖刷過程中床面的變化。為深入分析海上風電單樁基礎的沖刷過程及防沖刷措施的效果，凈曉飛等[38]利用FLOW-3D三維模擬軟件對有無防護下的單樁基礎進行數值模擬并和模型實驗對比。結果表明FLOW-3D可以較好地反映各防護措施下的沖刷過程，與模型實驗結果吻合良好。

在動床沖刷的數值模擬方面，ROULUND等[39]在OLSEN和MELAAEN[34]以及OLSEN和KJELLESVING[35]的工作基礎上，采用EllipSys3D模型對圓柱的局部沖刷開展了研究工作。該模型同樣采用雷諾平均的Navier-Stokes方程作為流體運動的控制方程并通過k-ε模型進行湍流封閉。數值模型中同樣考慮了推移質輸沙和懸移質輸沙并通過泥沙在底床上的質量守恒方程實現對局部沖刷地形的模擬。相關的數值模擬結果表明，該模型可以實現對沖刷過程準確模擬，所得到的圓柱上游方向平衡沖刷深度與實驗結果吻合較好，但圓柱下游方向的平衡沖刷深度與試驗結果存在30%的偏差。BAYKAL等[40]研究了懸移質輸沙和推移質輸沙對局部沖刷的影響作用。研究發現，當不考慮懸移質輸運時，平衡沖刷深度會減小50%，這說明懸移質輸沙對局部沖刷有重要的影響作用，在數值模擬中不可忽略。張曙光[41]利用FLOW-3D流體程序構建了三維數值水池，采用大渦模擬技術(LES)模擬了橋墩附近湍流流場。以內置的FAVOR技術追蹤河床形態的變化情況，得到了橋墩局部沖刷的完整形態。與橋墩現場實測資料的對比發現，模擬結果與實測的沖坑形態及最大沖深較為一致。

對于波浪條件下的圓柱局部沖刷數值模擬研究，LIU和GARCIA[42]通過Volume of Fluid方法(VOF Method)對波浪自由表面和水沙交界面進行捕捉，計算得到的平衡沖刷深度以及沖坑形態特征與試驗結果較為吻合。AFZAL等[43]用LSM方法(level-set method)，對波浪和均勻流條件下的圓柱局部沖刷問題開展三維數值模擬研究工作，發現該模型整體上能夠較好地預測沖坑的形態特征、沖坑位置和平衡沖刷深度。

在理論分析方面，DEY[44]基于馬蹄渦系結構是局部沖刷的主導因素以及沖刷為逐層發展的基本假定，提出了均勻和非均勻輸移質在清水和動床沖刷條件下局部沖刷深度隨時間變化的理論預測模型，相關的研究表明，該模型在均勻輸移質動床條件下對于平衡沖刷深度的預測結果偏大。MANES和BROCCHINI[45]基于湍流理論，并假設沖坑內渦的能量特征長度與沖坑深度相等，進而建立預測平衡沖刷深度的理論預測公式。HAFEZ[46]基于能量平衡原理，并將沖坑形狀簡化為三角形，建立了平衡沖刷深度理論預報模型，但模型中關于沖刷形態的假設與實際情況存在差異，導致該理論模型的預測精度不高。GAZI[47]在HAFEZ[46]的研究工作基礎上對其進行改進，模型中考慮了多種沖刷坑形態，提出了新的計算平衡沖刷深度模型。袁春光等[48]提出了“查圖法”和“微分迭代法”兩種方法來計算潮流條件下的樁基局部沖刷，潮流沖刷折減系數僅為0.4～0.6；而當漲急流速超過2.1倍臨界起動流速時，潮流沖刷折減系數達到0.9以上，因此使用沖刷折減系數時需要注意流速的大小，經過驗證計算結果與實測值吻合良好。

以上研究工作表明，對馬蹄渦等流動結構的預測精度以及水沙運動耦合的計算方法對數值模擬結果的精度起到決定性作用。與第二節情況相類似，目前無論是數值分析模型還是理論分析模型，其泥沙模塊基本都是基于松散均勻沙相關理論所建立的，對粘性土的輸運和沖刷特性考慮不足，導致相關的預報分析結果難以直接應用到工程實際中去。

4 現場實測

除了物理模型試驗和數值模擬，部分學者通過現場監測的方式，獲得水下垂直樁柱結構局部沖刷的實測數據。通過對數據的深入分析，建立了平衡沖刷深度對相關物理量的依賴關系，并與通過物理模型試驗所建立的經驗公式進行對比，從而對相關的經驗公式提出改進措施。

潘冬冬等[49]對湛江某海上風機基礎進行了3次現場局部沖刷實測，并根據沖刷數據開展了最大沖深、沖淤變化特征等參數的分析。依據現有的樁基基礎局部沖刷經驗公式與工程海域實測的水文數據，對海上風機基礎的最大沖深與沖刷半徑進行了計算，并進一步對經驗公式計算值和現場實測值進行了對比與分析，發現在砂袋與砂被復合保護下實測最大沖深相比計算值有明顯減小，沖刷半徑相對吻合。楊元平等[50]利用金塘大橋橋墩基礎沖刷現場實測資料，并結合該工程海域的地形掃測資料開展橋墩基礎局部沖刷研究，通過系統地分析解析出了往復潮流條件下橋墩基礎的一般沖刷及局部沖刷深度。張瑋等[51]和祁一鳴等[52]利用江蘇近海風機基礎局部沖刷現場實測數據，對近海風機基礎的局部沖刷情況進行了系統研究。張瑋等[51]和祁一鳴等[52]工作通過與現場實測數據的對比，均得出如下結論：采用韓海騫[20]提出的波浪作用下垂直樁柱局部沖刷預報公式獲得的局部沖刷深度相比其他經驗公式更為準確。

BOS等[53]對荷蘭北海某重力式平臺結構基礎的局部沖刷情況進行了現場監測。同時，對KHALFIN[54]經驗公式進行了改進，建立了新的沖刷平衡深度預報公式，通過與實測數據進行對比，發現改進的公式分析得到的平衡沖刷深度比實測數據大30%。此外，BOS等[53]還將現場監測數據與實驗室建立的經驗預報公式的結果進行對比，發現經驗預報公式計算得到的結果比現場監測數據大10%。WHITEHOUSE[55]對5處風電場的單樁基礎沖刷現場數據進行深入分析，發現現場觀測的最大沖刷S/D=1.8，大于通過DNV規范計算得到的結果(DNV規范計算得到的最大沖刷深度為S/D=1.3)，推測現場觀測數據與DNV規范計算值存在的差異是由極端海況條件所引起的。FIGEN[56]對Gunfleet Sands風場某直徑為4.7 m的風機基礎局部沖刷開展為期6個月的監測，實測數據表明，最大沖刷深度為S/D=1.7，也大于DNV規范的計算值。此外，FIGEN[56]還發現現場潮汐條件是誘發風機基礎局部沖刷的重要因素，DNV規范對潮汐流動條件考慮不足，導致計算得到的沖刷深度與實測數據存在較大差異。YAO[57]基于物理模型試驗獲得了結構物周圍應力放大系數，提出利用土體表觀沖刷速率，將實驗室物理模型試驗獲得的沖刷數據外推到原型的方法。但該方法對海床粗糙高度參數的選取較為敏感，同時外推的精度也受限于應力放大系數的測量精度，導致外推獲得的沖刷數據與現場監測數據存在一定的差異。

以上分析表明，現有的經驗公式預報得到的沖刷數據與現場實測數據均存在一定的誤差，這主要是由于相關經驗公式的取得基本都是基于實驗室松散均勻沙獲得的，難以考慮現場粘性土的局部沖刷特性；此外，影響局部沖刷的物理量眾多，現有經驗公式均進行了一定程度的簡化，未考慮這些物理量的聯合作用效果。

5 結語

本文針對垂直樁柱結構局部沖刷的相關研究工作進行了回顧與總結。目前，有關水下垂直樁柱局部沖刷研究工作主要以物理模型試驗為主，并建立了可考慮不同流動條件的局部沖刷特性預報公式。隨著計算機技術的發展，數值模擬也被廣泛應用到局部沖刷的研究工作中。由于局部沖刷的復雜性，導致目前所建立的經驗預報公式得到的結果與現場實測數據存在較大的差異，還需要開展更加深入系統的研究工作，建立更加準確的沖刷預報公式。通過總結和分析，相關結論如下：

(1)單樁基礎沖刷的物理模型試驗技術已經發展得相對成熟，但得到的經驗預測公式、預測結果與現場實測數據均存在較大的差異。因此，對如何將實驗室數據應用到工程現場需要進一步研究。

(2)現有經驗公式的取得往往都是基于松散均勻沙所獲得的，而實際工程中，海床往往廣泛分布著粘性效應比較明顯的底質，它們往往對應著截然不同的輸運和沖刷特性，因此需要開展更加深入的研究工作，使得實驗室獲得的結果更加具有工程應用價值。

(3)目前，數值分析模型已經可以很好地模擬馬蹄渦流動結構。與物理試驗類似，數值分析模型的泥沙運動模塊也是基于松散均勻沙所建立的。未來的研究工作中，應更加關注粘性土的輸運和沖刷特性，并建立相關輸運公式，對數值分析模型進行改進。

(4)實際工程中的單樁基礎在復雜海洋環境作用下會發生渦激振動，而目前的研究鮮有考慮到渦激振動對沖刷過程的影響。