基于BPE與自更新馬爾科夫鏈的耳鳴康復音樂合成方法*

方一鳴，何培宇，方安成，鄧茗月，潘帆

(四川大學電子信息學院,成都 610065)

引言

耳鳴是在沒有外界聲音刺激時的一種主觀聽覺感知[1]，可導致患者睡眠障礙、焦慮、注意力不集中，嚴重影響患者的生活質量。由于目前耳鳴發病機制尚不確定[2]，因此,還沒有治療耳鳴的明確手段。音樂療法是一種無創傷性的治療方法，由于其無副作用且方法柔和，而廣泛應用于耳鳴的臨床治療[3]。

目前，國外針對耳鳴的音樂療法主要包括Neuromonics耳鳴療法(neuromonics tinnitus treatment, NTT)[4]、切跡濾波音樂(tailor-made notched music,TMNM)療法[5]、海德堡神經音樂療法[6]。但上述幾種方法適用范圍有限、方案復雜，且使用的音樂都需重復播放[4,6-7]，易喚起患者的不良記憶及潛在負面情緒，達不到預期的減壓效果[8]。根據人工創作的音樂具有自相似特性[9]，程冉等[10]使用LS文法、陳杰梅等[11]基于五聲音階和混沌、徐媛媛等[12]基于IFS分形算法和分解和弦、金寧敏等[13]基于超混沌算法、蔡麗等[14]基于迭代系統、漆蕾宇等[15]使用IFS分形算法從音樂的曲調、節奏以及和聲三方面來生成理論上無限長，具有自相似特點，又不完全重復的耳鳴康復音樂。然而以上方法生成的音樂可聽性不足，并且存在著音高突變的缺陷。隨著技術的發展，Chen等[16]基于已有音樂片段和長短期記憶(LSTM)生成相似不完全重復，且能更好滿足耳鳴患者偏好的音樂，并臨床驗證了合成相似不重復音樂對治療耳鳴具有一定的效果。但是，該方法仍然存在著合成音樂不自然、拼接痕跡明顯、每首原始音樂都需要專門設計和訓練一組LSTM模型等問題，因而不便于臨床上的推廣應用。

針對上述問題，本研究提出一種以患者偏好的音樂為基礎，無需訓練且適用于所有原始音樂的耳鳴治療音樂合成方法。該方法使用字節對編碼對原始音樂主旋律聲部的信息進行編碼，將音樂表示成詞向量的組合形式，即音樂塊的組合形式。同時，本研究對馬爾科夫鏈狀態轉換過程可能會失去下一個轉移狀態的問題進行了改進，提出可以連續進行狀態轉換的自更新馬爾科夫鏈。將字節對編碼后的音樂塊作為自更新馬爾科夫鏈的狀態，利用自更新馬爾科夫鏈的狀態轉移來生成任意時長音樂。

仿真及試聽結果表明，本研究方法不僅理論上可以生成無限長、相似且不完全重復的滿足耳鳴治療的音樂，且生成模型簡單并具有普適性，生成的音樂聽感自然、無拼接痕跡、和原曲相似度高，可滿足音樂偏好的需求。

1 字節對編碼和自更新馬爾科夫鏈原理

1.1 字節對編碼

在音樂的生成過程中需要將音樂切分成塊，但是預先制定的切分方法并非適用于每首音樂，因此，本研究采用字節對編碼(byte pair encoding，BPE)自動學習音符及和弦間的最佳組合方式，使得切分后的音樂塊中的音符、和弦之間存在更強的依存關系。

BPE算法最早用于數據壓縮,原理是找到常見的可以組成單詞的子字符串，又稱子詞，然后將每個詞用這些子詞來表示。BPE中最基本的子詞就是所有字符的集合，如{a,b,…,z,A,B,…,Z}。之后，通過不斷統計文本中所有相鄰子詞的出現次數，選出出現頻率最高的一對子詞，并將這一對子詞組合起來視為一個新的子詞，使用文本中未出現過的符號代替這一對子詞，直到滿足某個停止條件，如:統計詞對的頻率最高不超過某個頻率閾值，其算法流程見圖1。

圖1 BPE算法流程Fig.1 BPE algorithm flow chart

1.2 自更新馬爾科夫鏈

1.2.1馬爾科夫鏈 馬爾科夫鏈可以根據當前狀態預測未來狀態，在多種狀態之間進行狀態轉移，本研究利用該特性實現理論上無限長音樂的生成。

馬爾科夫鏈是一組具有馬爾科夫性質的離散隨機變量集合，馬爾科夫性質指將來的狀態僅與當前時刻的狀態有關，而與過去時刻的狀態無關。即對于一個隨機過程{Xn,n∈T}，若隨機變量的取值都在可數集I內，對于任意的非負整數n∈T，條件概率滿足式(1)：

p(Xn+1|Xn,…,X1)=P(Xn+1|Xn)

(1)

則{Xn,n∈T}被稱為馬爾科夫鏈，可數集I∈Z被稱為狀態空間，馬爾科夫鏈在狀態空間內的取值稱為狀態。

當狀態也離散取值，系統在時刻n處于狀態i，在時刻n+1處于狀態j的概率可表示為：

τij=P[Xn+1=j|Xn=i]

(2)

此情況下，條件概率τij稱為轉移概率，其中，i,j∈I，這樣的馬爾科夫鏈稱為離散馬爾科夫鏈。若一個離散馬爾科夫鏈的狀態空間是有限的，則它所有的轉移概率可以組成一個馬爾科夫轉移概率矩陣：

(3)

1.2.2自更新馬爾科夫鏈 原音樂信息中，音樂塊是順序出現的，所以在使用馬爾科夫鏈進行狀態轉移時，除了最后一個音樂塊可能會出現缺少下一個轉移狀態的情況外，其余每個音樂塊至少都有一個轉移狀態。針對最后一個音樂塊沒有下一個轉移狀態的特殊情況，本研究利用音樂前后的相似性，將該音樂塊前一個音樂塊作為下一個狀態自動更新馬爾科夫鏈，并且為了避免生成音樂時進入死循環，觀察前一個音樂塊的轉移狀態數是否大于等于2，若小于2，則將此音樂塊的前一個音樂塊也作為一種轉移狀態更新馬爾科夫轉移矩陣，直到當前音樂塊的前一個音樂塊的轉移狀態數大于等于2為止。在原始音樂局部轉移狀態數較少時，也可使用該方法來豐富局部音樂塊轉移狀態，以生成更好的音樂。

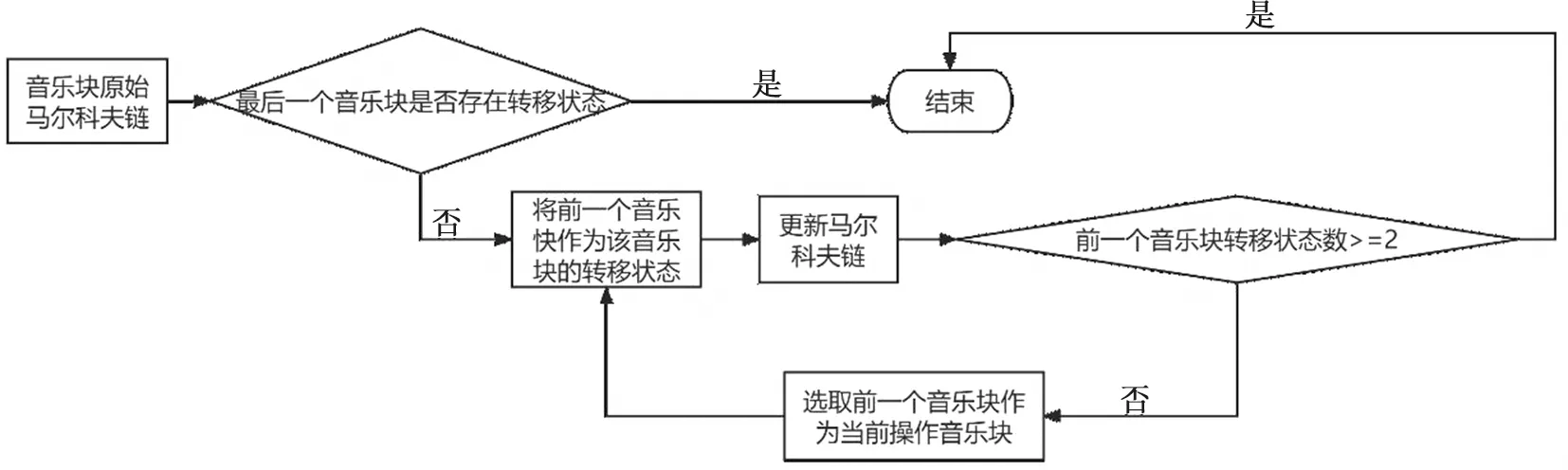
圖2 自更新馬爾科夫鏈原理Fig.2 Automatic updating Markov chain schematic diagram

2 耳鳴康復音樂合成方案

2.1 耳鳴康復音樂合成總體思路

音樂由一個或者多個聲部組成，在獨唱或者獨奏中只有一個聲部在發揮作用，而在合唱或者器樂合奏中樂曲由多個聲部組成。然而在多聲部中，通常只有一個演奏主旋律的聲部，其他聲部起伴奏作用。本研究在選取整首音樂后，都將第一個聲部作為主旋律聲部。首先,對MIDI音樂主旋律聲部的音符、和弦進行編號,采用字符對編碼將音樂分割成塊；其次，利用這些音樂塊來構造馬爾科夫轉移矩陣；最后，使用自更新馬爾科夫鏈生成任意長度的滿足耳鳴治療需求的音樂。圖3為本研究生成耳鳴康復音樂的流程圖。

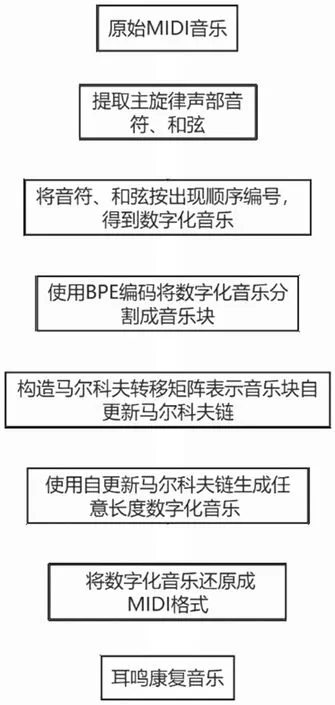
圖3 耳鳴康復音樂合成過程

2.2 原始MIDI音樂處理

MIDI是一種標準化的數據格式，易操作且數據存儲量小。因此，本研究選取的音樂皆為MIDI格式。本研究通過abcMIDI包，提取MIDI音樂主旋律聲部的音符、和弦，將音符、和弦按照前后出現的順序進行編號，并使用編號后的數字代替原音符、和弦，得到數字化后的音樂信息。

BPE最早用于數字壓縮，目前在自然語言處理中多被用于分詞。MIDI音樂由音符、和弦構成，音符、和弦在音樂中有一定的組成和順序關系，而雜亂無章的音符和和弦無法組合成悅耳的音樂。因此，本研究利用BPE可不斷統計迭代高頻出現的字節對的特點，對數字化后的音樂信息中出現的高頻音樂元素進行組合，將數字化后的音樂按照原有的順序劃分成音樂塊。

以編號后的音符、和弦為例。將一小段音樂的音符、和弦按照前后出現順序進行數字編號，并且使用編號后的數字代替原音符、和弦，得到一段數字文本：{3，3，3，28，16，3，3，3，28，3，10}。利用BPE進行編碼的步驟為：設定BPE停止條件為相鄰字節對最高出現次數不超過1，將單個數字作為子詞，統計相鄰子詞出現次數，此時“3，3”出現頻率最高，使用“-1”來代替“3，3”，文本變為：{-1，3，28，16，-1，3，28，3，10}，此時“3，28”出現頻率最高，使用“-2”來代替“3，28”，文本變為：{-1，-2，16，-1，-2，3，10},此時“-1，-2”出現頻率最高，使用“-3”來代替“-1，-2”，文本變為：{-3，16，-3，3，10}。最后，所有相鄰子詞的出現次數都為1，得到最終的文本數據：{-3，16，-3，3，10}。BPE解碼時按照相反的順序進行更新替換即可。

本研究對數字化后的音樂信息，統計其相鄰數字出現的頻率，將出現頻率最高的數字對進行合并，替換成音樂信息中未出現過的數字，直到統計數字對的最高頻率不超過設定閾值。實驗表明，當閾值設置為1時，生成音樂的效果最好。

2.3 音樂生成模型構建

本研究使用馬爾科夫轉移矩陣描述生成音樂的自更新馬爾科夫鏈。在馬爾科夫轉移矩陣中，將每個音樂塊作為一種狀態，實驗中假設下一個音樂塊出現的概率只和前一個出現的音樂塊有關。

馬爾科夫轉移矩陣構建過程如下：首先，統計BPE編碼后的音樂塊種類N，并對音樂塊按照出現順序進行1至N編號，重復出現的音樂塊編號和第一次出現的該音樂塊編號一樣。統計N種音樂塊之間的轉移頻數，得到N種音樂塊之間的轉移概率。然后構建一個N×N大小的矩陣，矩陣最左上角元素為(1,1),矩陣元素(i,j)表示編號為i的音樂塊轉移到編號為j的音樂塊的概率。觀察此N×N大小的矩陣元素(N,N)的值是否為0。若為0，則使用自更新馬爾科夫鏈的更新規則添加新的狀態轉移，并以此更新狀態轉移矩陣。最后得到生成的馬爾科夫轉移矩陣，隨機選擇一個音樂塊作為開始，根據此馬爾科夫轉移矩陣生成任意長度的音樂(在耳鳴的臨床治療中，可根據患者的治療時間來生成相應時長的對應音樂)。

2.4 使用MIDI技術合成音樂

首先，將馬爾科夫鏈生成的任意長度的音樂進行BPE解碼；然后，按照數字與原始音符、和弦的對應關系將數字還原成原始的音符、和弦；最后賦予這些音符、和弦和原始音樂一樣的音樂信息，即音色、音符持續時間、音符速度等，如此便獲得和原曲相似且任意長度的滿足耳鳴治療需求的音樂。

3 仿真結果及試聽分析

3.1 仿真結果分析要素

本研究從1/f波動和分形兩個角度對合成音樂進行客觀分析。1/f波動分析表明，合成音樂能讓人感到愉悅放松并具有較高的舒適感，音樂的分形分析表明，合成音樂具有相似不重復性，即合成音樂像人工創作的音樂一樣具有前后自相似的特點[17]，能夠避免喚醒耳鳴患者的記憶，以上分析表明，本研究合成音樂作為耳鳴康復音樂具有較強的合理性。最后通過試聽分析，對合成音樂的聽覺效果進行主觀檢驗，表明合成的音樂流暢、自然。

3.2 音調值和音符時值1/f波動分析

1/f波動是一種具有舒適感的波動，可通過譜密度S(f)與頻率f的關系表示，譜密度S(f)表示信號在頻率f處的均方根變化。具體見式(4)：

S(f)∝f-β

(4)

對上式兩邊取對數，得到：

log(S(f))∝-βlog(f)

(4)

研究表明，大多數令人愉悅的音樂都是1/f波動，且幾乎所有的音樂旋律都在模仿1/f波動，當0.5<β<1.5時，信號即滿足1/f波動[18]。

圖4是生成音樂的音調值和音符時值的功率譜擬合曲線，兩個擬合曲線對應的β值分別是0.8987、0.9019，均在(0.5,1.5)范圍內，即生成的音樂是一種舒適且可讓人感到放松的1/f波動信號。

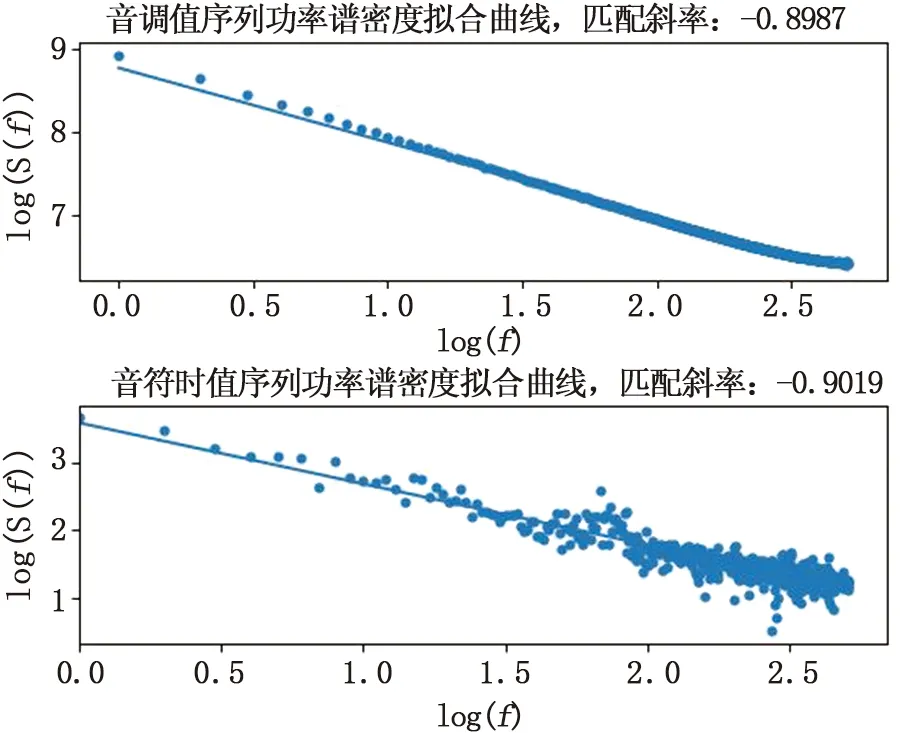
圖4 音調值序列和音符時值序列功率譜密度擬合曲線

3.3 音樂分形分析

3.3.1分形維度分析 分形特征之一是自相似但不完全重復,即整體與局部的高度相似[19]，可以此檢驗合成的耳鳴康復音樂是否滿足自相似、非重復的要求。在音樂中，相鄰音符的音程i及其出現的頻率F(i)若滿足下述函數，則此關系稱為分形。其中，C是常數，D是音樂的分形維度。

(6)

將上述等式兩邊同時取對數，得到：

logF(i)=C′-Dlogi

(7)

由此可知，logi和logF(i)是以-D為斜率的線性關系。

圖5是本研究生成音樂中i與F(i)之間的對數關系的擬合曲線，可見，logi與logF(i)基本呈線性關系，斜率為-2.207。

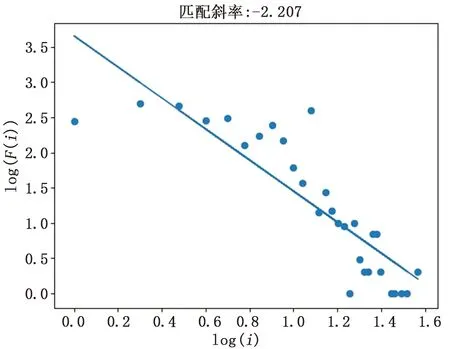
圖5 音樂分形結構分析

3.3.2旋律輪廓分析 旋律輪廓描述了旋律的整體形狀，比準確的音程信息更容易認識與記憶。本研究使用音符作為最小單位來代表旋律輪廓。圖6是生成較短時間的音樂的旋律輪廓，其中縱坐標是音符的音調值，橫坐標是音符的序列值。圖7是生成較長時間音樂的旋律輪廓。觀察兩段旋律輪廓可以看出，音樂旋律前后相似且旋律自然，生成的長時間音樂并非音符的簡單重復。音樂的音高在一定范圍內變化，未出現音高突變的情況。即生成的音樂滿足相似且不重復的特性，無音高突變，滿足耳鳴治療音樂的要求。

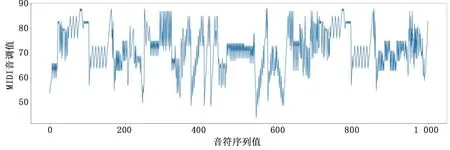
圖6 短時間音樂的旋律輪廓

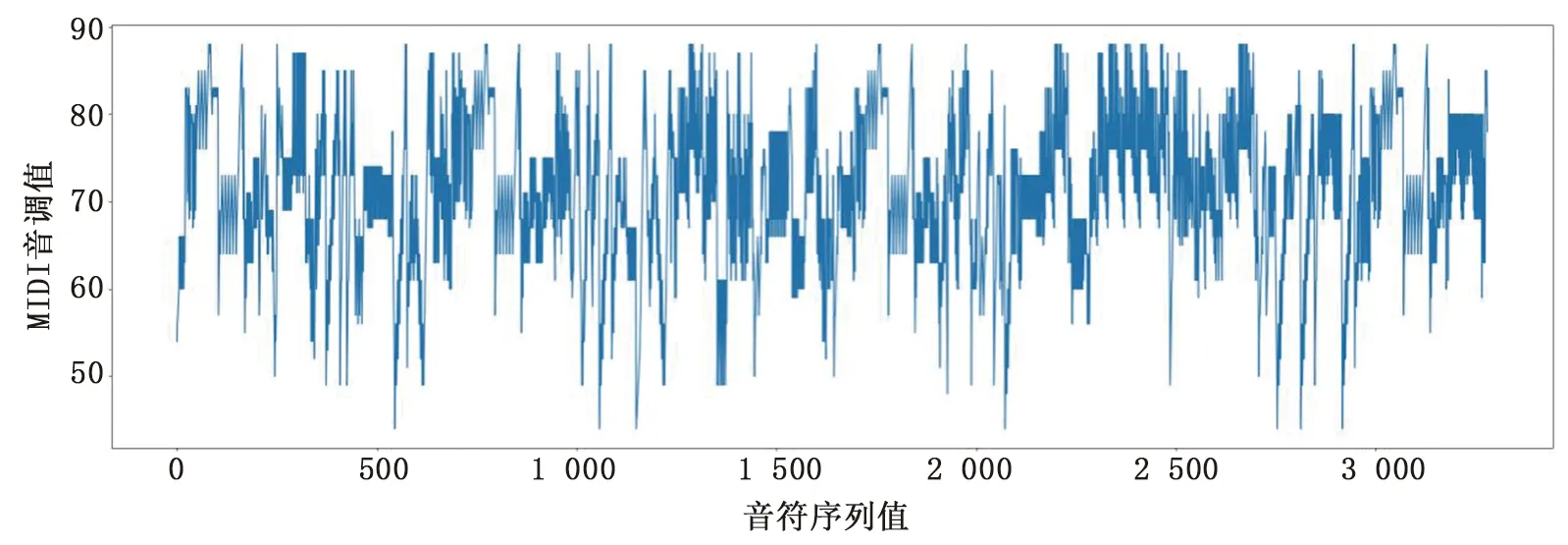
圖7 長時間音樂的旋律輪廓

3.4 試聽分析

本次試聽實驗采用文獻[16]和原始音樂拼接的音樂作為對照。假設一段2 min的音樂為耳鳴患者的偏好音樂，分別根據該原始音樂使用本研究和文獻[16]的方法合成時長為30 min的音樂Frag_1、Frag_2，并將這段2 min的原始音樂首尾相連，拼接成30 min的音樂Frag_3。30名試聽人員根據試聽結果分別在相似不重復、重復、流暢、舒緩、與原曲最相似五項要素中選擇出最符合該音樂特性的要素。其中，相似不重復和重復只能二選一，與原曲最相似這項要素，Frag_1、Frag_2之間只能選擇一個，Frag_3不參與該項選擇。流暢與舒緩全選、全不選、選其一皆可。

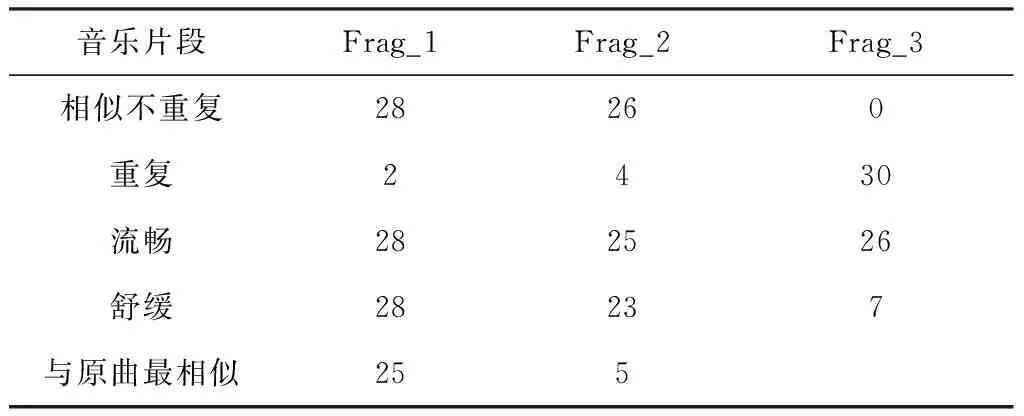
表1 音樂片段試聽

試聽結果表明，本研究合成的音樂具有令人舒緩、相似不重復的特性，與仿真結果相吻合。同時彌補了臨床上需反復播放音樂，以及現有方法生成音樂不自然的缺陷。然而該試聽結果是對耳鳴康復音樂的主觀檢驗，還未完全應用到實際臨床中，后續在臨床中還需根據患者的具體情況調節相關參數，以達到更好的效果。

4 總結

本研究提出了一種基于BPE和馬爾科夫鏈的耳鳴康復音樂合成新方法。該方法簡單，可生成任意時長且適用于所有MIDI格式的音樂，便于臨床上的推廣。仿真及試聽結果表明，該方法生成的音樂是一種能讓人感到舒緩的1/f波動，在滿足患者個性化偏好的同時，整體相似但不重復，彌補了臨床上需重復播放有限時長音樂的問題，在聽感體驗上也更加流暢自然。因此，本研究提出的音樂合成方法對使用音樂療法治療耳鳴具有一定的借鑒意義。