弧形類蜂窩芯層面外等效力學性能研究

殷圣地，湯雙清，李響*,,2，仇琨，段宇，陳濤

弧形類蜂窩芯層面外等效力學性能研究

殷圣地1，湯雙清1，李響*,1,2，仇琨1，段宇1，陳濤1

（1.三峽大學 機械與動力學院，湖北 宜昌 443002； 2.石墨增材制造技術與裝備湖北省工程研究中心（三峽大學），湖北 宜昌 443002）

為提高蜂窩結構面外承載能力，從創新設計角度，提出一種弧形類蜂窩夾芯結構，并對其面外力學性能進行研究。首先，采用胞元理論對弧形類蜂窩夾芯結構進行簡化，運用材料力學的知識并結合能量法，推導其面外等效模量解析表達式。然后，將弧形類蜂窩芯層結構與傳統蜂窩芯層結構進行對比，在相同等效密度下，通過具體數據驗算，發現弧形類蜂窩芯層的面外剪切模量有顯著地提高。同時，推導出雙壁厚弧形類蜂窩面外等效模量表達式。最后，運用數值模擬分析，得到該結構的仿真值，經過理論值與仿真值對比，發現兩者相對誤差在10%之內，證明推導出的面外等效模量理論公式的準確性。

弧形類蜂窩夾芯；面外等效模量；能量法；數值模擬

夾層結構材料具有輕質高強的優點，在航空航天、船舶等領域中有著極其重要的應用價值。隨著國內外學者的不斷探索，近年來，國內外許多學者致力于新型蜂窩結構究，并取得了較大的進展，廣泛地應用于工程。

隨著工程技術不斷地提高，傳統蜂窩逐漸不能滿足部分特殊工況的要求，研發新型蜂窩結構成為熱點。經國內外研究學者不斷探索，提出了許多新型蜂窩結構[1-4]。Simone DelBroccolo等[1]將內凹六邊形和正六邊形這兩種不同的蜂窩結構進行交替排布，得到一種混合零泊松比蜂窩陣列結構。并通過壓縮實驗可知該結構在面內剛度不變的前提下，其抗壓強度提高了2倍。即在不降低結構變形能力的前提下，提高了結構的承載能力。JosephN Grima等[2]在原有六邊形蜂窩的基礎上對其進行改進，得到了一種拉脹六角蜂窩結構，發現該結構在面外的楊氏模量要遠大于水平方向，并且可以產生具有圓柱形曲率的彎曲變形。王瑋[3]通過遺傳算法對八邊形蜂窩進行改進，得到一種新型八邊形蜂窩，并對其推導等效力學性能，通過仿真驗證該結構對比原結構在一定程度上減小了應力的集中。蔣偉[4]等人通過對蜂窩進行改進，獲得一種負泊松比的蜂窩結構，得到一種環形蜂窩，并推導出該結構等效彈性模量。

目前，對新型蜂窩芯體的力學性能研究最有效的方法是理論分析、實驗測試和數值模擬相結合以得到正確的等效力學性能參數公式[5-18]。沈建邦等[5]在環形蜂窩[4]結構的基礎上，提出了一種具有負泊松比效應的可變弧角曲邊內凹蜂窩結構，利用能量法給出了曲邊內凹蜂窩結構的面內橫縱向等效彈性模量和等效泊松比的解析公式，該結構在不同的幾何尺寸的條件下，得到其等效彈性模量隨著尺寸變化而變化的結論。李響等[6-8]通過六邊形蜂窩結構的基本單元的優化排列，得到類蜂窩結構，對該結構及夾層結構進行力學性能進行推導與特性分析及優化，通過數值模擬對理論值進行驗證，驗證具有可靠性。周星馳等[9]從應力與應變的角度并運用能量法對圓形胞元蜂窩芯層面外剪切模量進行公式推導，結合實驗與仿真驗證其面外剪切模量公式正確性。吳建均[10]等人基于材料力學中材料的連續性、小變形等基本假設，推導出泡沫紋復合夾芯結構的等效彈性常數。對于面外等效剪切模量，kelsey等[11]利用單位力法和單位位移法求解六邊形蜂窩芯子的上限與下限。Gibson等[12]給出了等壁厚蜂窩結構面外參數。趙劍等[13]則通過最小勢能原理與最小余能原理，得到與kelsey結果同樣的上下限。富明慧等[14]則在上述基礎上，通過位移邊界條件求得的上限與kelsey結果下限一致，同樣給出了等壁厚與雙壁厚六邊形蜂窩芯層面外剪切模量的確定值。王梁等[15]通過有限元軟件ABAQUS分析不同的幾何尺寸的X型蜂窩芯層，并得到該結構受外夾角的影響最大，蜂窩芯層等效彈性模量與泊松比效應模量隨著外夾角增大而增大。齊佳旗等[16]在低速載荷下沖擊CFRP蒙皮－鋁蜂窩夾層結構，使用有限元軟件ABAQUS對該結構進行仿真，實驗結果與仿真結果相似，驗證其仿真具有準確性。

經過上述文獻，可得國內外研究學者為蜂窩芯層結構做出了重大的貢獻，為后來者提供了多種研究方法，但對于圓弧形蜂窩力學性能的研究卻是極少，本文通過創新構型的角度，構建弧形類蜂窩芯層結構，基于能量法從應變的角度推導該結構面外等效模量，利用數值模擬驗證面外等效模量理論公式的正確性，對弧形類窩芯層結構研究提供理論基礎。

1 弧形類蜂窩夾芯結構設計

夾層結構分別由上下面板、蜂窩夾芯組成。夾芯在該結構中主要用于承載剪切力，能夠較好地抵抗橫向剪切力引起的變形。本文從創新構型角度出發構建弧形類蜂窩夾層結構。通過弧線單元與直線單元的優化排列，得出圖1所示結構。為了進一步深入研究，該結構單胞的幾何參數進行表示為：四個邊長長度為，四個弧形的外徑、內徑分別為、，四個弧長的的圓心角都為1，邊長與水平的角度為2，垂直于坐標系，平面的新型蜂窩的厚度為，如圖2所示。

圖1 弧形類蜂窩芯層結構

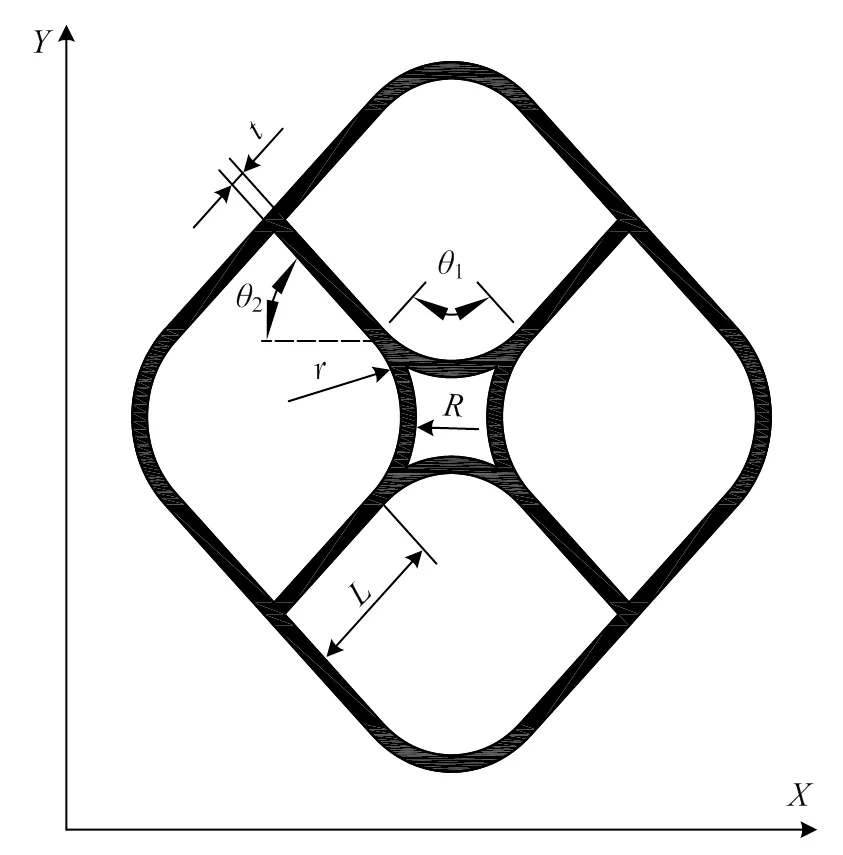
圖2 弧形類蜂窩芯層尺寸參數

2 弧形類蜂窩夾芯面外力學特性分析

2.1 等壁厚弧形類蜂窩夾芯結構面外等效彈性模量

由于蜂窩芯層結構作為多孔結構的典型代表，是一種不連續、不均質的面板。為了進一步研究蜂窩芯層結構力學性能，根據胞元理論將弧形類蜂窩芯層簡化，推導等效模量理論公式，蜂窩芯層結構等效模量主要分為面外等效模量和面內等效模量。相比于面內等效模量，面外等效模量遠大于面內等效模量，因此可得，蜂窩芯層結構面外抗載荷能力大于蜂窩芯層面內抗載荷能力。為深入研究芯體結構功能應用，建立蜂窩芯體的面外等效模量模型是必要的。根據胞元理論將弧形類蜂窩芯層結構進行簡化，得到基本單元體（如圖3所示），為了有效研究弧形類蜂窩結構，取2為π/4。在基本單元體上施加縱向載荷（如圖4所示）。可推導單元體的蜂窩壁應變為：

式中：σ為基本單元體上的應力，GPa；ε為基本單元體的應變；為蜂窩壁單位長度上承載的載荷，N；為基本單元體胞壁厚度，mm；E為弧形類蜂窩基本單元體材料的彈性模量，GPa。

弧形類蜂窩蜂窩芯體單元體承受的總載荷為：

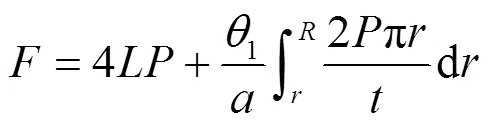
式中：為常數，＝90°，為四個邊長長度，mm；為四個弧形外徑，mm；為四個弧形內徑，mm；1為四個弧長的的圓心角，rad。

將基本單元體等效為均質體，即基本單元體等效為具有均勻性、連續性的面板。則可推導出，在基本單元體總載荷作用下，均質體的應變為：

式中：εcz為均質體的應變；S為均質體的面積，mm2；Fcz為均質體的彈性模量，GPa；F為均質體上的總載荷，N。

圖4 單壁厚芯體的基本單元體面外縱向載荷

根據前文所述，基本單元體等效為均質體，兩者的應變相等，因此可得：

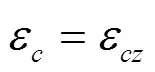
故可推導得：

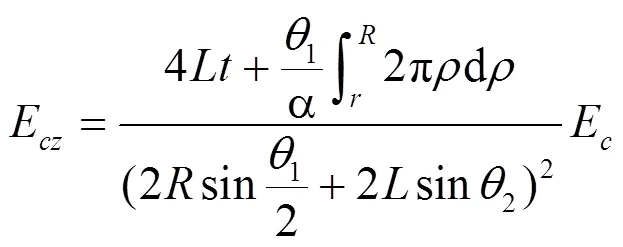
2.2 等壁厚弧形類蜂窩夾芯結構面外等效剪切模量

當弧形類蜂窩夾芯受到面外剪切力時，剪切力τ以剪流的形式在基本單元體胞壁上進行傳遞。假定單元體胞壁上剪切力的作用方向為軸，面外剪切力分布均勻，可推導基本單元體的方向上的總載荷為：

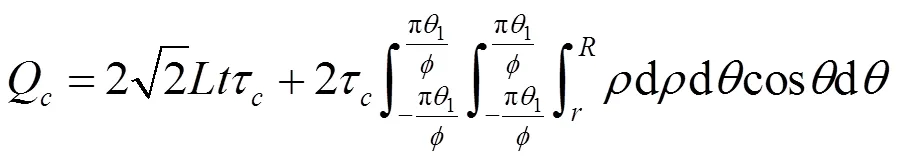
如圖5所示，由于單元體關于、軸對稱，在剪切力的作用下，蜂窩壁單位體積的應變能為：

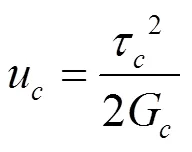
式中：uc為單元體的單位體積應變能，J/mm3；Gc為基本單元體材料的剪切模量，GPa。

可推導出基本單元體的應變能為：

式中：為常數，＝180°；U為基本單元體的應變，J；v為基本單元體體積，mm3；h為基本單元體的高度，mm。

根據上文所述，基本單元體承受面外剪切力與面板上的作用力相等，即Q＝Q，通過已知的條件，可推導出，在橫向剪切力的作用下，均質體的應變為：

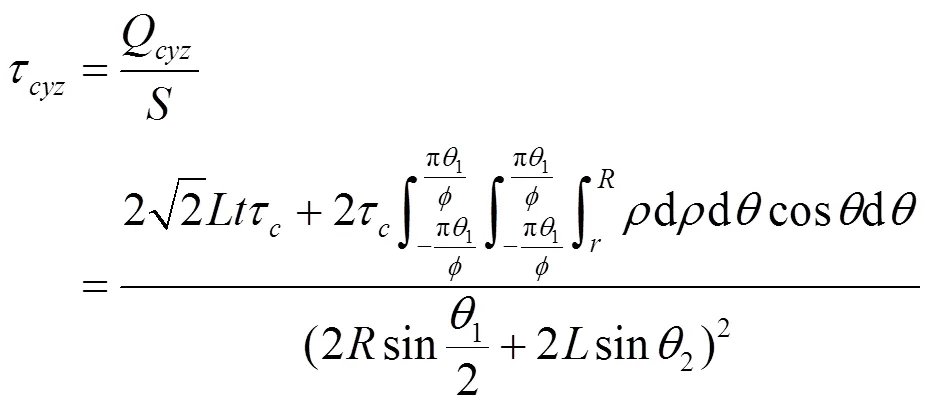
式中：τ為均質體上的剪切力，GPa；Q為均質體上的總剪切力，N。

則均質體在橫向剪切力的作用下，應變能為：

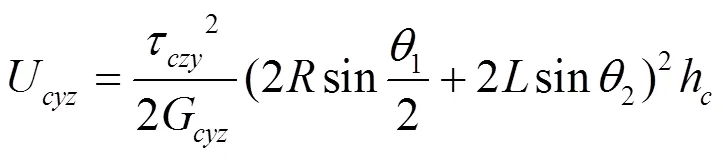
式中：U為均質體上的應變能，J；G為均質體的剪切模量，GPa；τ為均質體上的切應力，GPa。

根據前文可得U＝U，結合述式（9）和式（11），可得均質體的等效剪切模量為：

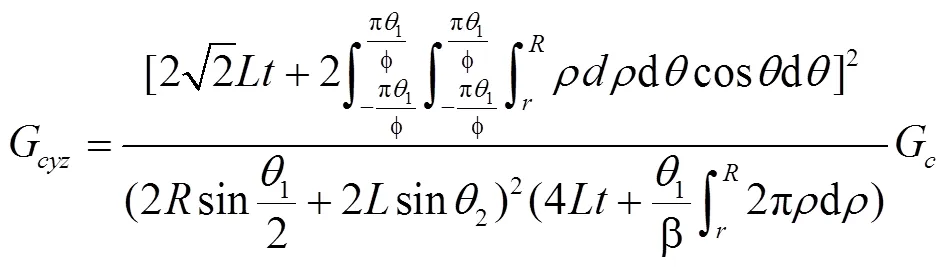
3 算例分析與對比

通過已推導理論公式，研究同等密度下，弧形類蜂窩芯體與傳統蜂窩芯體力學性能，需要推導出兩者基本單元體的密度。根據前文，可得基本單元體的體積為：

基本單元體的質量為：

基本單元體等效模型的體積為：

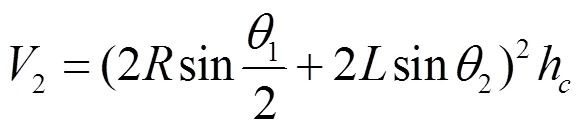
基本單元體等效模型的質量為：

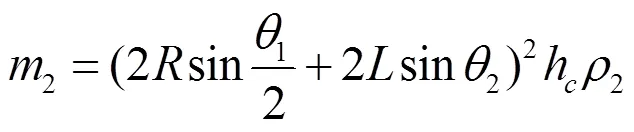
式中：2為基本單元體等效模型材料的密度，g/mm3。

根據等效前后質量守恒原理，可得1＝2，因此可得：

取1＝60°、2＝45°、＝，可將式（12）簡化為：

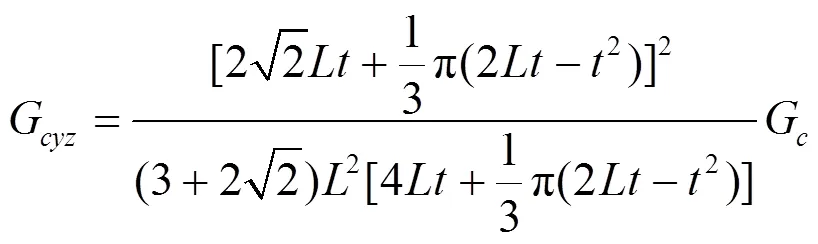
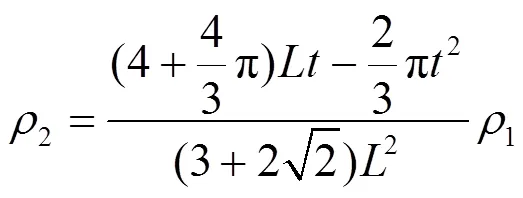
將具體數據代入公式，經過推導可得，在相同的密度條件下，弧形類蜂窩芯層面外剪切模量有顯著的提高，對于抵抗受外剪切力，弧形類蜂窩芯層結構具有更優良的性能。

4 雙壁厚弧形類蜂窩芯層等效模量

4.1 雙壁厚弧形類蜂窩芯層等效彈性模量

傳統的蜂窩芯層主要以等壁厚與雙壁厚兩種不同的結構應用于工程。為了推進應用進程，推導雙壁厚弧形類蜂窩芯層等效彈性模量。該結構單胞如圖6所示，簡化結構，可得基本單元體如圖7所示。施加軸方向載荷，如圖8所示，由此可得雙壁厚弧形類蜂窩芯層總載荷為：

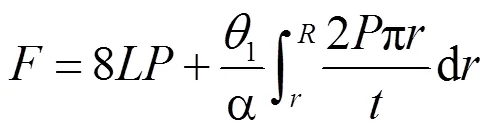
弧形類蜂窩芯層基本單元體材料的彈性模量為E，可推導出弧形類蜂窩芯層基本單元體的應變為：

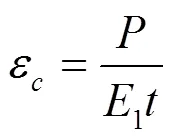
圖6 雙壁厚弧形類蜂窩芯層單胞尺寸參數

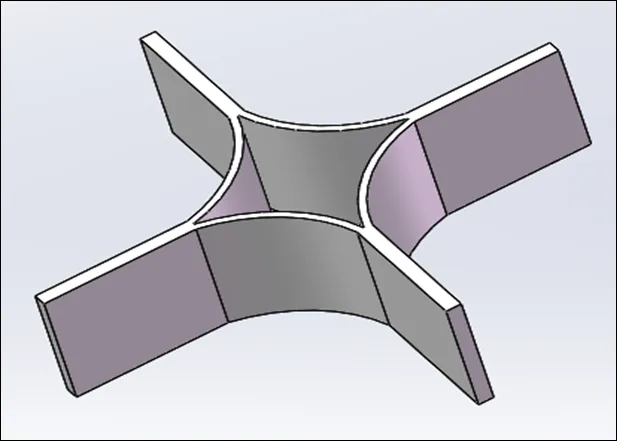
圖7 單壁厚芯體的基本單元體

圖8 單壁厚芯體的基本單元體面外縱向載荷

均質體的應變為：

由于基本單元體與均質體的應變相等，即ε＝ε，結合以上公式，可得雙壁厚新型蜂窩芯層等效彈性模量為：

4.2 雙壁厚弧形類蜂窩芯層等效剪切模量

對于雙壁厚弧形類蜂窩芯層等效剪切模量的推導，由于弧形類蜂窩芯層關于、軸對稱，可得其剪流的情況，如圖9所示，當軸受力時，雙壁厚弧形類蜂窩芯層受到的總載荷為：

基本單元體的單位體積應變能為：

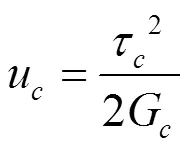
基本單元體的應變能為：

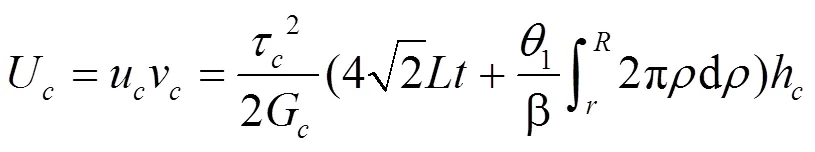
均質體在橫向剪切力的作用下應變能為：

由于基本單元體與等效均質體的應變能相等，即U＝U，結合以上公式，可得雙壁厚弧形類蜂窩芯層等效剪切模量為：

5 仿真驗證

采用ABAQUS軟件對該結構面外等效模量理論公式進行驗證，上下面板、蜂窩芯層均采用solid實體單元，弧形類蜂窩芯層的材料參數為：密度＝2.78×1012g/m3，彈性模量＝71 GPa，泊松比＝0.33。將上下面板表面與芯層上下表面綁定，對上剛性面板施加、方向作用力均為0.1 MPa，＝0.3 mm，＝＝6 mm，1＝60°，2＝45°。

通過ABAQUS對弧形類蜂窩芯層面外等效模量進行數值計算，如圖10、圖11所示，可得其在仿真計算下的面外等效模量。

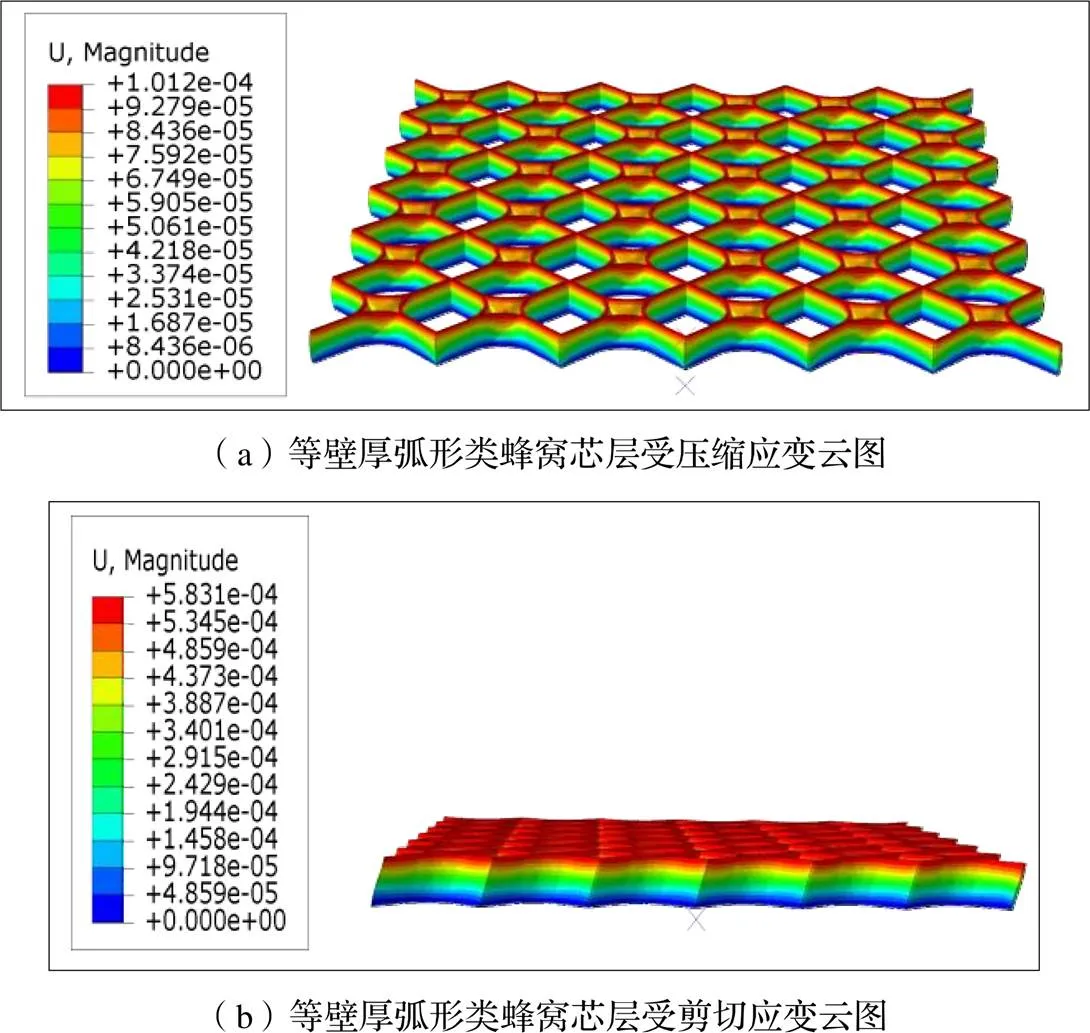
圖10 等壁厚弧形類蜂窩芯層應變云圖

圖11 雙壁厚弧形類蜂窩芯層應變云圖

仿真值與理論值之間的相對誤差在10%以內，如表1和表2所示。從而可得，弧形類蜂窩芯層面外等效力學模量的理論公式具有可靠性，可作為工程應用的理論依據。同時，將雙壁厚蜂窩芯層結構與單壁厚蜂窩芯層結構進行對比，發現雙壁厚蜂窩芯層結構承載能力有顯著的提升。

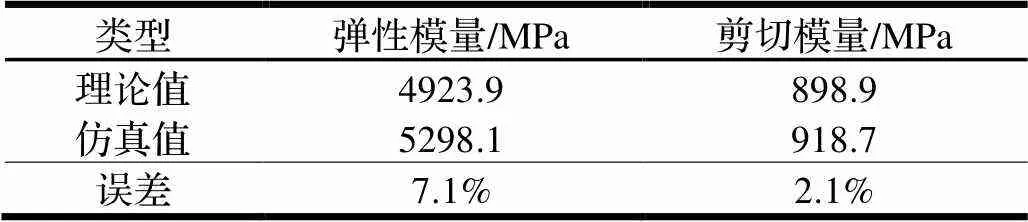
表1 等壁厚新型蜂窩芯層結構的相對誤差

表2 雙壁厚新型蜂窩芯層結構的相對誤差

6 結論

（1）由于蜂窩芯層結構在實際應用中存在等壁厚夾芯結構與雙壁厚夾芯結構，筆者使用經典胞元理論及材料力學的知識對兩種不同壁厚新型蜂窩芯層結構面外等效模量進行推導；

（2）通過閱讀國內外研究學者對傳統蜂窩芯層結構的研究成果文獻，獲得傳統蜂窩芯層結構面外等效模量公式，在相同密度下，對比兩者的面外剪切模量，可得到弧形類蜂窩芯體面外抗剪切能力大于傳統蜂窩芯體，可用于剪切力較大的特殊工況；

（3）運用有限元商業軟件ABAQUS，對比弧形類蜂窩芯層結構的面外等效模量公式，理論值與仿真值之間的誤差在10%以內，從而可得，經過經典胞元理論及材料力學知識對兩種不同壁厚新型蜂窩芯層結構面外等效模量表達解析式具有準確性，可應用于實際工程。

[1]Del Broccolo S，Laurenzi S，Scarpa F. AUXHEX-A Kirigami inspired zero Poisson’s ratio cellular structure[J]. Composite Structures，2017，176：433-441.

[2]Grima J N，Oliveri L，Attard D，et al. Hexagonal honeycombs with zero Poisson's ratios and enhanced stiffness[J]. Advanced Engineering Materials，2010，12（9）：855-862.

[3]王瑋. 零泊松比蜂窩結構的設計及應用[D].大連：大連理工大學，2019.

[4]蔣偉，馬華，王軍，等. 基于環形蜂窩芯結構的負泊松比機械超材料[J]. 科學通報，2016，61（13）：1421-1427.

[5]沈建邦，肖俊華. 負泊松比可變弧角曲邊內凹蜂窩結構的力學性能[J]. 中國機械工程，2019，30（17）：2135-2141.

[6]李響，周幼輝，童冠，等. 超輕多孔類蜂窩夾心結構創新構型及其力學性能[J]. 西安交通大學學報，2014，48（9）：88-94.

[7]陳永清，仇琨，李響. 類蜂窩夾層結構振動特性分析及應用研究[J]. 機械，2022，49（1）：9-15，36.

[8]李響，潘志宇，李銳，等. 輕質高強類蜂窩夾層結構力學性能分析及優化[J]. 機械，2021，48（11）：1-9.

[9]周星馳，唐振剛，周徐斌，等. CFRP圓形胞元蜂窩芯層面外剪切模量[J]. 復合材料學報，2018，35（10）：2777-2785.

[10]吳建均，王永靜，謝敬堯，等. 泡沫波紋復合夾心梁等效彈性常數的推導及其振動特性研究[J]. 西安交通大學學報，2018，52（11）：73-80.

[11]Kelsey S，Gellatly R A，Clark B W. The shear modulus of foil honeycomb cores：A theoretical and experimental investigation on cores used in sandwich construction[J]. Aircraft Engineering and Aerospace Technology，1958，10（11）：294-301.

[12]Gibson L J，Ashby M F，Schajer G S，et al. The mechanics of two-dimensional cellular materials[J]. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences，1982，382（1782）：25-42.

[13]趙劍，謝宗蕻，安學峰，等. 蜂窩芯體材料面外等效彈性模量預測與分析[J]. 航空材料學報，2008（4）：94-100.

[14]富明慧，徐歐騰. 關于蜂窩芯體面外等效剪切模量的討論[J]. 固體力學學報，2014，35（4）：334-340.

[15]王梁，劉海濤. X型內凹蜂窩結構的拉伸力學行為研究[J]. 機械強度，2020，42（4）：896-900.

[16]齊佳旗，段玥晨，鐵瑛，等. 結構參數對CFRP蒙皮－鋁蜂窩夾層板低速沖擊性能的影響[J]. 復合材料學報，2020，37（6）：1352-1363.

Equivalent Mechanical Properties Outside the Layer of Arc-shaped Honeycomb Core

YIN Shengdi1，TANG Shuangqing1，LI Xiang1,2，QIU Kun1，DUAN Yu1，CHEN Tao1

( 1.College of Mechanical and Power Engineering, China Three Gorges University, Yichang443002, China; 2.Hubei Engineering Research Center for Graphite Additive Manufacturing Technology and Equipment (China Three Gorges University), Yichang 443002, China )

In order to improve the out-of-plane bearing capacity of the honeycomb structure, an arc-shaped honeycomb-like sandwich structure was proposed from the perspective of innovative design, and its out-of-plane mechanical properties were studied. Firstly, the arc-shaped honeycomb-like sandwich structure is simplified by using the cell theory, and the analytical expression of its out-of-plane equivalent modulus is deduced by using the knowledge of material mechanics and the energy methods. Then, the arc-shaped honeycomb-like core layer structure is compared with the traditional honeycomb-like core layer structure. Under the same equivalent density, it is found that the out-of-plane shear modulus of the arc-shaped honeycomb-like core layer is significantly improved through specific data verification. At the same time, the out-of-plane equivalent modulus expression of the double-wall-thickness arc-like honeycomb is derived. Finally, using numerical simulation analysis, the simulation value of the structure is obtained. After comparing the theoretical value and the simulation value, it is found that the relative error between the two is within 10%, which proves the accuracy of the derived theoretical formula of the out-of-plane equivalent modulus.

arc-shaped honeycomb sandwich；out-of-plane equivalent mechanical model；energy method；numerical simulation

O342

A

10.3969/j.issn.1006-0316.2022.11.001

1006-0316 (2022) 11-0001-08

2022-02-28

國家自然科學基金青年科學基金（51305232）

殷圣地（1997－），男，湖北黃梅人，碩士研究生，主要研究方向為輕量化技術，Email：1572429532@qq.com。*通訊作者：李響（1979－），男，湖北黃梅人，博士，副教授，主要研究方向為輕量化技術、結構優化設計、數值模擬技術、結構強度與可靠性等，Email：lixiangcfy@ctgu.edu.cn。