改進的指數函數方法求時空分數階混合(1+1)維KdV方程的新精確解

陳兆蕙，陽平華*

(廣州城市理工學院計算機工程學院，廣東 廣州 510800)

受“孤立波”現象的啟發，荷蘭數學家Korteweg和deVries在研究關于淺水問題中的小振幅長波運動時合作發現了KdV方程。這是一種典型的非線性色散波動方程，物理學中的很多現象如：固態物理、冷等離子的磁流波、聲波的傳播、量子場、離子-聲子波、非諧振晶格振動等都可以用這種方程來解釋[1]。研究這類方程的精確解能給物理學提供可靠依據，也能加強數學和其他學科之間的緊密聯系，所以研究它的精確解很重要。由于對分數階偏微分的研究比整數解偏微分方程應用范圍更為廣泛、也更能準確表述物理和其他學科的特性，因此目前有(G'/G)-展開法和一般的tanh方法[2-6]、首次積分法[7-8]、改進的Riccati方法[9]、擬設法[10]、改進的Kudryashov方法[11-12]、Hirota方法[13-14]等研究分數階偏微分方程，并且得到了多種不同類型的解。

本文在其他作者研究工作[1-17]的基礎上，探討一類時空分數階混合(1+1)維KdV方程

(1)

其中a0,a1,a2是非線性系數，β是色散系數，這些系數都不為零且α滿0<α≤1.當a0=a2=0，方程(1)變成了時空分數階KdV方程[15]，張志惠[15]使用指數展開法求解出了該方程的精確解；當a0=0，方程(1)變成了時空分數階KdV-mKdV方程[16]，賴曉霞[16]采用改進后的指數展開法研究了該方程的精確解，并采用符號計算軟件給出了解的三維立體圖形。本論文同文獻[15-16]相比，方程項數增加，難度增大；同文獻[17]相比，雖然研究的是同一個方程，但是文獻[17]采用的是首次積分法，本文采用改進的指數函數方法[15-16]。研究方法不同，本論文拓展了方程(1)的新精確解，且新精確解更加豐富。

Jumarie的修正Riemann-Liouville分數階導數[15-16]按照如下定義：

定義1

定理1[15]

Jumarie的修正Riemann-Liouville分數階導數具有以下性質：

1 時空-分數階混合(1+1)維KDV方程

首先對方程(1)作分數階變換，令

(2)

這里的w是待定常數。將(2)式代入(1)式，有-wu′+a0u′+a1uu′+a2u2u′+βu?=0，對上式積分一次，并且令積分常數為零，得到

(3)

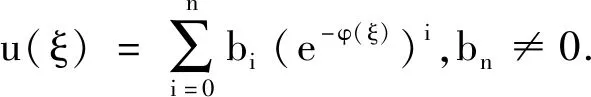
綜合考慮式(3)中u″和u3最高階次數須達到平衡，即3n=n+2，得出n=1，從而

(4)

且φ(ξ)滿足下列常微分方程

φ′(ξ)=pe-φ(ξ)+μeφ(ξ)+λ

(5)

其中p,μ,λ為待定常數。

將式(4)和式(5)代入式(3)，有

合并(e-φ)i(i=0,1,2,3)的相同冪次項，有

令(e-φ)i(i=0,1,2,3)的各個系數等于零，得到一個關于b0,b1,w的代數方程組：

由上述方程組，得到b0,b1和w滿足如下方程

由于約束條件不一樣，得到的解也不相同。下面分情況討論方程的新精確解。

2 時空-分數階混合(1+1)維KdV方程的新精確解

第一種情形：

p=1,λ2-4μ>0,λ≠0,μ≠0,得到參數值如下：

此時

φ1(ξ)=

有新精確解

(6)

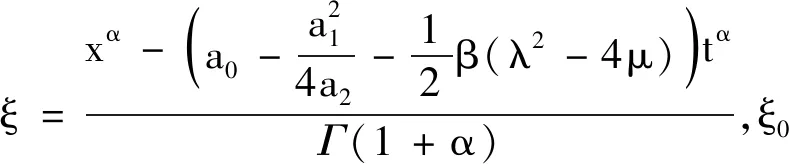
第二種情形：

p=1,λ2-4μ<0,λ≠0,μ≠0,得到

參數值如下：

此時

φ2(ξ)=

得新精確解

(7)

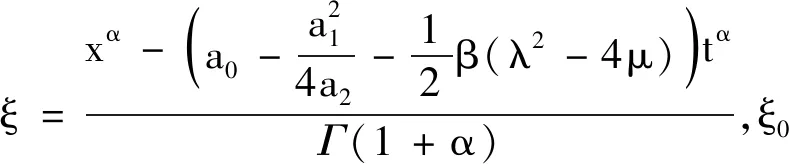
第三種情形：

p=1,λ2-4μ>0,λ≠0,μ=0,得到參數值如下：

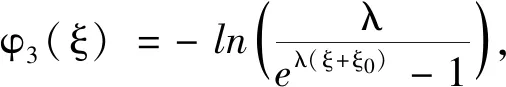
(8)

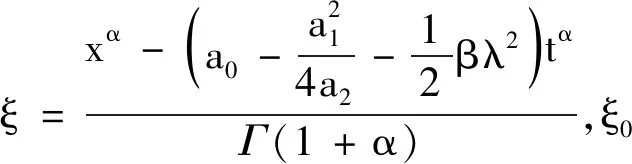
第四種情形：

p=1,λ2-4μ=0,μ≠0,λ≠0，得到參數值如下：

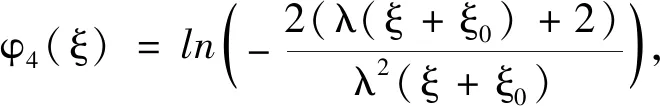
(9)

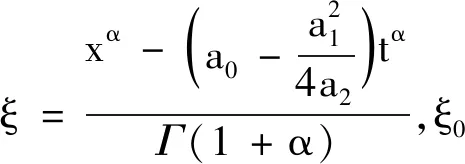
第五種情形：

λ=0,p>0,μ>0,得到參數值如下：

此時

或

得新精確解

(10-1)

或

u5-2(ξ)=b0+b1e-φ5-2(ξ)

(10-2)

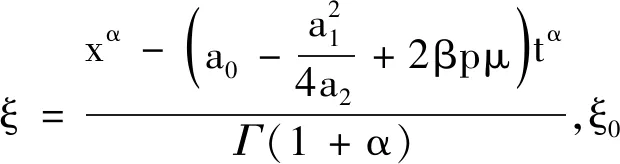
第六種情形：

λ=0,p>0,μ<0,得到參數值如下：

此時

φ6-1(ξ)=

或

φ6-2(ξ)=

得新精確解

或

(11-2)

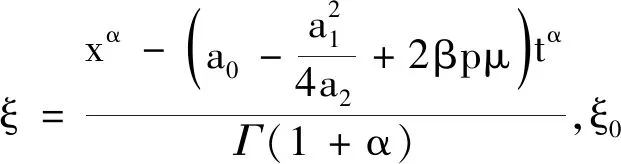
第七種情形：

λ=0,p<0,μ>0,得到參數值如下：

此時

φ7-1(ξ)=

或

φ7-2(ξ)=

得新精確解

(12-1)

或

(12-2)

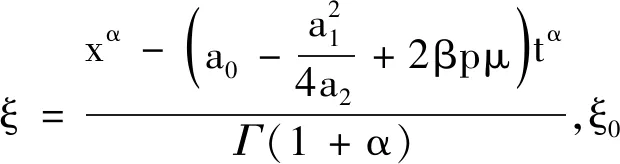
第八種情形：

p=1,μ=0,λ=0,λ2-4μ=0，得到參數值如下：

此時

φ8(ξ)=ln(ξ+ξ0)

得新精確解

(13)

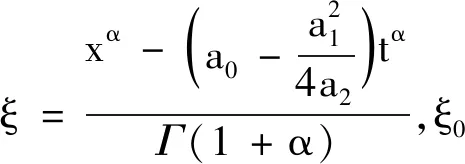
3 圖形繪制

為了更直觀表示圖形，這里對具有代表性的第一種情形下的精確解進行計算機仿真.取

限制0≤t≤6,0≤x≤8,得到圖形如下：

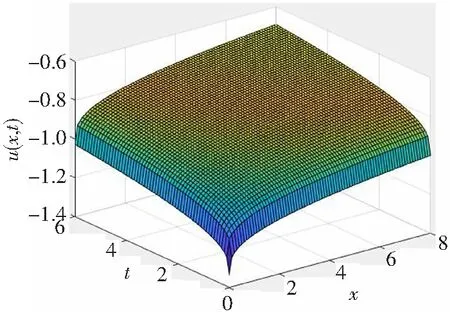
圖1 α=0.3時第一種情形下的精確解圖形Figure 1 The exact solution of the graph in the first case with α=0.3

圖2 α=0.9時第一種情形下的精確解圖形Figure 2 The exact solution of the graph in the first case with α=0.9

4 結論

本文使用改進的指數函數展開法擴充了時空分數階混合(1+1)維KdV方程的新精確解。說明改進的指數函數方法對于求解分數階方程有實用性和優越性。但是文中這類時間分數階方程可否使用其他方法如：不變子空間方法、動力系統分支法等方法來研究它的新的精確解呢？這是后續研究的方向。