如何重新擺棋子

★蔣成法

【問題】下面的方格圖中（如圖1），橫著看，上、下兩邊各有3 枚棋子；豎著看，左、右兩邊也各有3 枚棋子。如果要使每邊棋子的個(gè)數(shù)盡可能少，并且四周每橫行、豎行里的棋子仍然有3枚，該怎么辦呢？

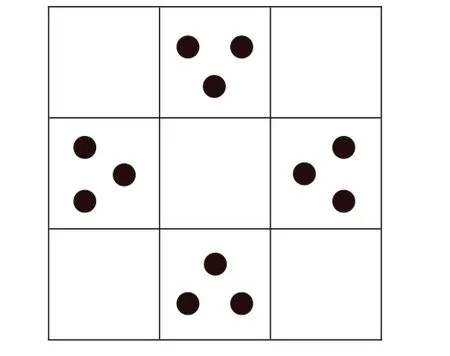
圖1

【思路點(diǎn)睛】題目的意思是讓我們從圖中拿出一些棋子，但每邊仍然要保持3 枚。為此，我們可以親自試一試。在試驗(yàn)的時(shí)候，棋子的位置一定要移動(dòng)，如圖2：

圖2

還能不能再減少呢？接著試一試，將棋子從10枚減少到8枚，如圖3：

圖3

那這算不算最少的呢？不是，因?yàn)檫€可以將棋子的個(gè)數(shù)減少到6枚，如圖4：

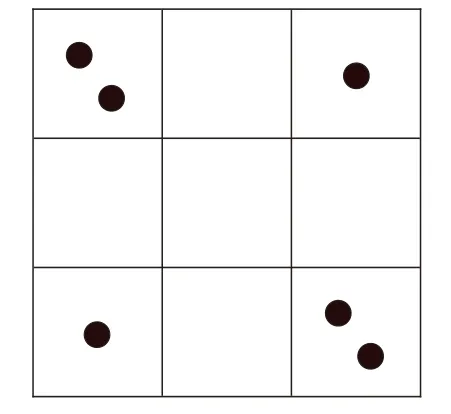
圖4

學(xué)會(huì)了以上的操作，下面我們?cè)偬嵘幌骂}目的難度。比如，圖5 的方格圖，每邊都有10 枚棋子。如果拿掉4 枚棋子，怎樣重新擺放，才能使每邊仍然有10 枚棋子？如果拿掉6枚棋子呢？

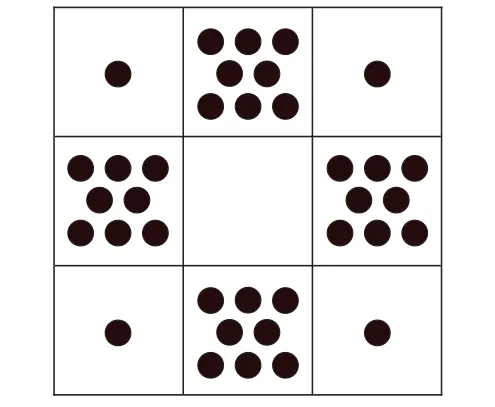
圖5

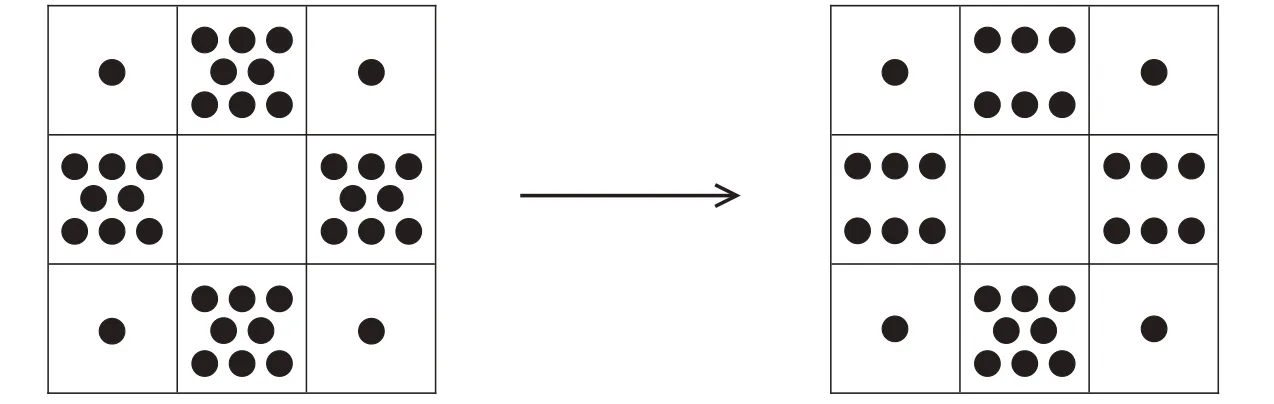
如果拿掉四個(gè)角的4 枚棋子，此時(shí)每邊只剩下中間的8枚棋子。怎樣才能讓每邊仍然有10枚棋子呢？聰明的你肯定想到了，從中間的8 枚棋子中拿出2 枚棋子放在四個(gè)角上，得到：

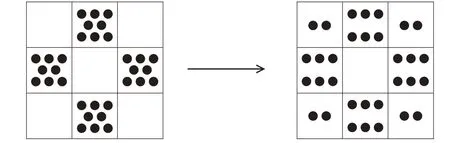
如果拿掉6枚棋子，我們可以從三邊中間的8枚棋子中各拿出2枚，然后再觀察。

因?yàn)橐浞掷弥睾系牟糠郑晕覀儾僮鞯姆椒ê芏唷１热纾瑥南逻叺?枚棋子中拿出2枚放到右下角，再從右邊中間的6枚中拿出2枚放到右上角，最后從上面中間的6枚中拿出2枚放到左上角，此時(shí)正好每邊都有10枚棋子。

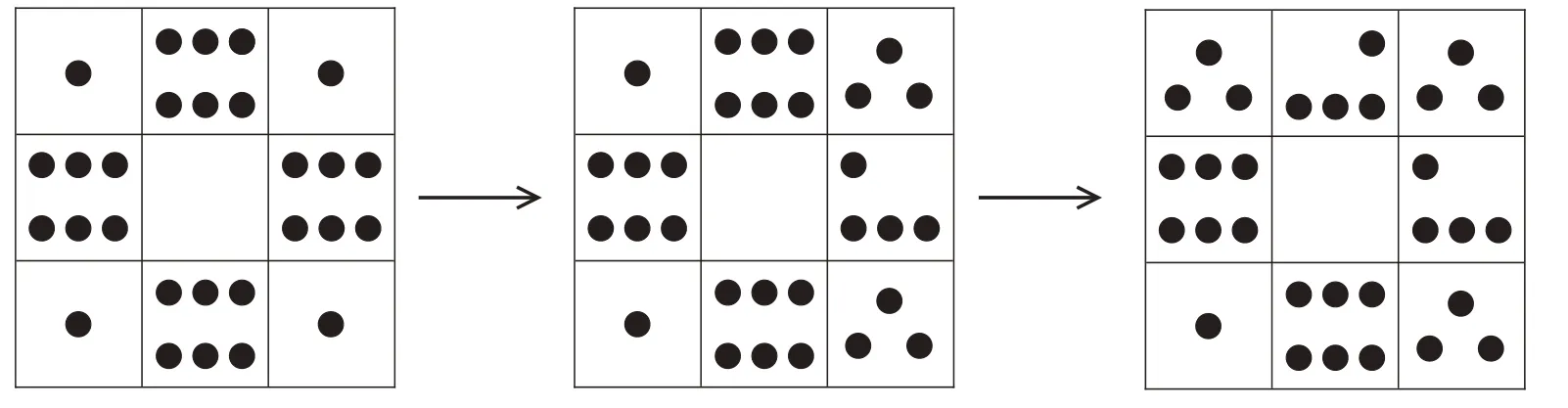
聰明的你，親自動(dòng)手試一試吧！