單箱雙室變截面波形鋼腹板組合連續箱梁自振特性試驗研究

榮學亮 歐陽靖 焦明偉 趙文丁 郭峰

1.石家莊鐵道大學 道路與鐵道工程安全保障教育部重點實驗室，石家莊 050043；2.石家莊鐵道大學 土木工程學院，石家莊 050043；3.吉林省交通規劃設計院，長春 130021

波形鋼腹板組合連續箱梁將波紋鋼板代替傳統的混凝土腹板，結構自重減輕10%～30%，從而減少了恒載內力，在一定程度上提高了抗震性能。同時，波紋鋼板具有褶皺效應［1］，一方面降低了腹板的抗壓剛度，提高了頂底板預應力施加效率，另一方面增大了腹板的抗剪屈曲性能，提高了腹板的抗剪能力［2］。1986 年，法國建成了世界上第一座三跨波形鋼腹板連續組合箱梁橋，隨后這種新型橋梁結構在國內外橋梁工程領域陸續得到了廣泛關注［3-6］。近年來，地震、風致振動、列車經過產生的車橋耦合振動和噪聲振動等動力學問題對橋梁結構影響顯著，有必要對這種橋梁結構開展動力學方面的研究。

文獻［7］對波形鋼腹板I 型組合梁的固有頻率開展了試驗研究和有限元分析。文獻［8］通過能量變分法推導了波形鋼腹板預應力混凝土箱梁的固有頻率，并利用數值模擬進行了參數分析。文獻［9］對單箱單室變截面波形鋼腹板組合梁開展了彎曲振動研究。文獻［10］通過模型試驗和有限元數值分析相結合的方法分析了變截面波形鋼腹板連續箱梁橋的動力特性，并提出了考慮波形鋼腹板剪切變形計算豎向基頻的修正估算公式。文獻［11］研究了波形鋼腹板組合箱梁褶皺效應對其動力特性的影響，分析了各類波形鋼腹板組合梁橋的地震響應。文獻［12］對等截面單箱多室波形鋼腹板預應力混凝土組合連續梁橋開展了動力特性試驗研究。文獻［13］研究了結構參數對大跨度波形鋼腹板箱梁橋動力特性的影響。文獻［14］提出了新型波形鋼腹板組合箱梁不同模態等效阻尼比計算方法。文獻［15］利用Hamilton 原理和能量變分法建立等截面波形腹板鋼箱組合連續梁的振動方程。

綜上，國內外文獻主要針對等截面波形鋼腹板組合連續箱梁動力特性開展研究，但國內建成的此類橋梁大多數為變截面波形鋼腹板組合連續箱梁。本文設計制作了三跨單箱雙室變截面波形鋼腹板連續組合試驗箱梁開展室內動力測試試驗，然后建立有限元模型進行數值模擬，并分析橫隔板和邊中跨徑比對試驗梁自振特性的影響。

1 試驗梁動力測試概況

鄄城黃河公路大橋為國內一座變截面波形鋼腹板組合箱梁橋，本文以該橋為原型，參照其橫截面尺寸按照1∶9 進行縮尺制作試驗梁。試驗梁梁長10 m，跨徑布置為（2.6+4.8+2.6）m。試驗梁橫截面和立面見圖1。在邊支座設置厚度為200 mm 的端橫隔板，邊跨跨中設置厚度100 mm 的橫隔板，中支座處設置厚度500 mm 的橫隔板，中跨跨中設置厚度100 mm 的橫隔板。

圖1 試驗梁橫截面和立面（單位：mm）

根據國內實際工程常用1 200 型波形鋼腹板，按照1∶4 相似比，模型中波形鋼腹板波長300 mm，波高50 mm，鋼板厚4 mm，波折角為114°。將帶孔的波形鋼腹板穿入鋼筋，埋入頂底板混凝土，形成埋入式開孔鋼板連接件進行澆筑連接，保證結構整體受力。頂底板按照設計規范要求采用C40 混凝土，波形鋼腹板采用Q235 低碳優質鋼材，彈性模量為206 GPa。頂底板共布置了4 根體內預應力筋，2 根體外預應力筋，預應力筋采用公稱直徑為15.24 mm 的1 860 級鋼絞線。

由于試驗梁的剛度比較大，試驗采用瞬態激振法進行動力測試。利用東華DH5922 動態信號采集分析系統對采集的動力信號進行分析，拾振器采用中國地震局工程力學研究所研發的941B 型拾振器（豎向）。為了防止關注的模態丟失，避免將激振點布置在結構前幾階模態的結點上，測點布置見圖2。

圖2 測點布置（單位：mm）

通過動力測試試驗，利用自互功率譜法獲得試驗模型梁前三階自振頻率和振型。為了避免誤差，分別進行三次動力測試試驗，取平均值作為試驗值。

2 自振特性試驗研究

2.1 建立有限元模型

為了分析單箱雙室變截面波形鋼腹板連續組合箱梁與傳統混凝土腹板連續箱梁自振特性的變化，采用ABAQUS（2020）建立單箱雙室變截面波形鋼腹板試驗模型梁和混凝土腹板試驗模型梁。在剪切荷載作用下，兩種模型梁腹板上的剪力相等，混凝土腹板厚度為100 mm，其余幾何尺寸基本一致。根據結構的形式和受力特點，混凝土頂底板選擇8 節點一階實體單元（C3D8R）模擬，波形鋼腹板采用4 節點殼單元（S4R）模擬，普通鋼筋和預應力鋼筋采用2 節點桁架單元（T3D2）模擬。不考慮普通鋼筋和預應力與混凝土之間的滑移，波形鋼腹板與頂底板通過Tie 綁定，采用Em?bedded的關系將鋼筋嵌入到混凝土中。計算預應力損失后，利用降溫法模擬有效預應力。分析動力特性時，混凝土、鋼筋、鋼材均采用線彈性模型，采用C40 混凝土，普通鋼筋采用HRB335，波形鋼腹板采用Q235鋼材。劃分網格后，在單箱雙室變截面波形鋼腹板連續組合箱梁中，共有126 793個實體單元（C3D8R），26 634 個殼單元（S4R），46 584 個桿單元（T3D2）；在混凝土腹板連續箱梁中，共有161 477 個實體單元（C3D8R），45 488 個桿單元（T3D2）。兩片模型梁的有限元模型單元數接近，網格劃分精度和單元規格基本相同，能夠避免計算產生的誤差。

單箱雙室變截面波形鋼腹板試驗模型梁自振頻率有限元計算值和試驗值對比見表1。可知，自振頻率有限元計算值和試驗值比較接近，相對差值在6%以內，說明有限元模型建立合理，數值分析方法可靠。試驗值均大于有限元計算值的原因是制作試驗梁時中跨橫隔板和邊跨橫隔板未拆除模板，導致試驗值偏大。

表1 自振頻率有限元計算值和試驗值對比

2.2 有限元結果分析

根據有限元數值計算結果，得到單箱雙室變截面波形鋼腹板連續組合箱梁和傳統混凝土腹板連續箱梁一階自振頻率分別為57.6、65.5 Hz，二者一階自振頻率相差12.1%。混凝土腹板連續箱梁自重為10.87 t，由波形鋼腹板代替混凝土腹板形成單箱雙室變截面波形鋼腹板連續組合箱梁后自重為8.95 t，減輕了17.7%。根據結構動力學可知，結構的基頻與結構自重、抗彎剛度有關。由于波形鋼腹板存在褶皺效應，忽略波形鋼腹板對連續組合箱梁抗彎剛度的影響，其抗彎剛度比傳統混凝土腹板連續箱梁減小了20.2%。與傳統混凝土腹板連續箱梁相比，波形鋼腹板連續組合箱梁抗彎剛度的減小幅度比結構自重大，從而導致波形鋼腹板連續組合箱梁一階自振頻率小于傳統混凝土腹板連續箱梁。

兩種箱梁模型前十階自振頻率對比見圖3。可知，在第三階以后，單箱雙室變截面波形鋼腹板連續組合箱梁自振頻率均比傳統混凝土腹板連續箱梁小。由于單箱雙室變截面波形鋼腹板連續組合箱梁受腹板剪切變形、相互耦合效應以及剪力滯效應的影響，其自振頻率與傳統混凝土腹板連續箱梁相比，隨著階數的增加，相對差值變化不穩定。

圖3 兩種箱梁模型前十階自振頻率對比

2.3 有限元計算值、試驗值與規范估算值對比

JTG D60—2015《公路橋涵設計通用規范》［16］規定，連續梁橋的自振頻率（基頻）適合采用有限元方法計算，常規結構也可采用估算公式，并給出了連續梁自振頻率（基頻）的估算公式。

沖擊力引起正彎矩和剪力效應時自振頻率f1為

沖擊力引起負彎矩時自振頻率f2為

式中：l為計算跨徑；E為彈性模量；Ic為跨中截面慣性矩；mc為跨中單位長度質量。

按照規范采用式（1）計算出單箱雙室變截面波形鋼腹板連續組合箱梁自振頻率為66.8 Hz，與試驗值（57.7 Hz）和有限元計算值（57.6 Hz）相差約15.7%。

通過文獻［17］可知，式（1）產生的誤差是因為估算公式沒有考慮波形鋼腹板的剪切變形和剪切剪滯耦合效應對組合連續梁自振頻率的影響。因此，本文參照根據能量變分原理和Hamilton 原理提出基于JTG D60—2015的自振頻率修正估算公式，即

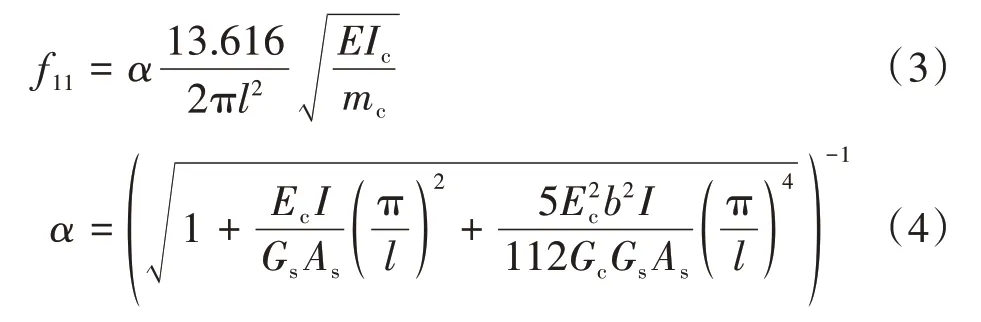
式中：f11為沖擊力引起正彎矩和剪力效應時自振頻率修正值；Ec為混凝土材料的彈性模量；I為頂底板的截面慣性矩之和；b為混凝土頂板箱中凈跨的一半；Gs為波形鋼腹板的修正剪切模量；Gc為混凝土材料的剪切模量；As為波形鋼腹板的剪切面積。

其中，式（4）二次方根中的第二項為波形鋼腹板剪切變形的影響，第三項為剪切剪滯耦合效應的影響。按照式（3）計算得到單箱雙室變截面波形鋼腹板連續組合箱梁的自振頻率為50.6 Hz，與試驗值和有限元計算值相差12.3%，修正公式計算值比試驗值和有限元計算值更保守，且比式（1）計算的誤差小3.4%左右，證明修正公式更合理。同理對式（2）進行修正，得到

式中：f22為沖擊力引起負彎矩時自振頻率修正值。

3 參數分析

為研究橫隔板和邊中跨徑比對試驗梁自振特性的影響，采用ABAQUS對試驗梁進行動力仿真分析。

3.1 橫隔板

基于單箱雙室變截面波形鋼腹板試驗模型梁設計6 種方案：方案1，僅去掉中支點橫隔板；方案2，僅去掉端支點橫隔板；方案3，僅去掉中跨橫隔板；方案4，去掉邊跨橫隔板；方案5，去掉中跨、邊跨、中支點、端支點橫隔板；方案6，原有模型。6 個方案有限元模型自振頻率和振型見表2。可知，方案5的一階自振頻率明顯小于其他方案，不同方案前十階振型以豎彎和扭轉為主。對于前三階振型，方案1—方案4，以及方案6前三階振型以豎彎為主，方案5 前三階振型以扭轉和橫彎為主。

表2 6種方案有限元模型自振頻率和振型

前三階豎彎自振頻率見圖4。可知：①對于一階豎彎自振頻率，方案2—方案4自振頻率均大于方案6，方案1、方案5自振頻率均小于方案6，方案1自振頻率降幅最大，為3.58%；②對于二階豎彎自振頻率，方案1—方案5 自振頻率均大于方案6；③對于三階豎彎自振頻率，方案2—方案4 自振頻率均大于方案6，方案1、方案5自振頻率均小于方案6，方案1自振頻率降幅最大，為7.37%。這說明設置中支點橫隔板對單箱雙室變截面波形鋼腹板連續箱梁一階和三階豎彎自振頻率的提高貢獻較大，有助于改善箱梁的動力性能。其余位置設置的橫隔板對箱梁豎彎自振頻率影響均較小，原因是其余位置橫隔板的厚度和高度比中支點橫隔板小，豎向剛度較弱。

圖4 前三階豎彎自振頻率

前三階扭轉自振頻率見圖5。可知：①方案1—方案5 的前三階扭轉自振頻率均小于方案6，方案5 降幅超過50%；②對于一階扭轉自振頻率，方案1、方案2分別降低46.93%、12.81%，方案3、方案4 降幅較小，分別降低12.65%、0.36%；③對于二階扭轉自振頻率，方案1、方案2 分別降低17.07%、27.43%，方案3、方案4降幅較小，分別降低11.00%、0.05%；④對于三階扭轉自振頻率，方案1、方案2 分別降低29.08%、40.03%，方案3、方案4 降幅較小，分別降低11.38%、7.39%。這說明設置橫隔板能夠有效提高單箱雙室變截面波形鋼腹板連續箱梁的扭轉自振頻率，其中，中支點橫隔板和端支點橫隔板能顯著提高箱梁前三階扭轉自振頻率。原因是中支點、端支點橫隔板與混凝土頂底板和波形鋼腹板連接構成框架結構，同時承受支座的約束，產生了較大的抗扭框架效應，提高了箱梁抗扭剛度。而中跨與邊跨布置的橫隔板與整體箱梁沒有形成較大的框架效應，因此對箱梁扭轉自振頻率的提高有限。

圖5 前三階扭轉自振頻率

前三階橫彎自振頻率見圖6。由表2 和圖6 可知：①對于一階橫彎自振頻率，方案1、方案2、方案4、方案5、方案6均小于方案3的自振頻率，方案5自振頻率降幅最大，為71.56%；②方案4 和方案6 在前十階振型中并未出現二階橫彎和三階橫彎，因此僅分析其他幾個方案。對于二階和三階橫彎自振頻率，方案1、方案2、方案5 均小于方案3 的自振頻率。這說明設置橫隔板能顯著提高單箱雙室變截面波形鋼腹板連續箱梁的橫彎自振頻率，由于中跨和邊跨橫隔板對整體箱梁橫向約束能力弱，因此對箱梁橫彎自振頻率的提高貢獻很小。

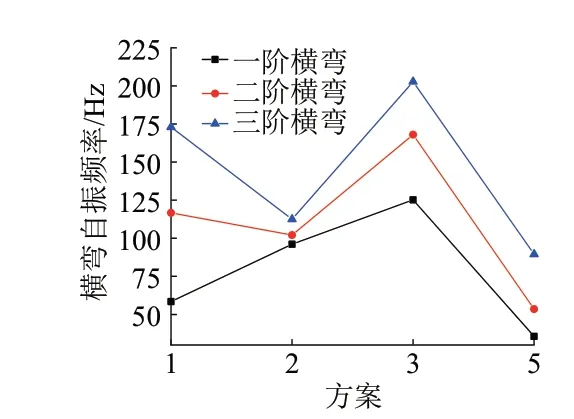
圖6 前三階橫彎自振頻率

3.2 邊中跨徑比

不同邊中跨徑比下兩種模型梁前三階豎彎和扭轉自振頻率見圖7。

圖7 不同邊中跨徑比的自振頻率對比

由圖7可知：

1）不同邊中跨徑比下，單箱雙室變截面混凝土腹板模型梁的一階豎彎自振頻率均大于單箱雙室變截面波形鋼腹板模型梁；單箱雙室變截面波形鋼腹板模型梁的前三階豎彎自振頻率均小于單箱雙室變截面混凝土腹板模型梁；模型梁前二階豎彎自振頻率隨著邊中跨徑比的增加而增加，第三階豎彎自振頻率在邊中跨徑比為0.55后呈下降趨勢。

2）不同邊中跨徑比下，單箱雙室變截面波形鋼腹板模型梁的一階扭轉自振頻率均略大于單箱雙室變截面混凝土腹板模型梁，而單箱雙室變截面波形鋼腹板模型梁的高階扭轉自振頻率均小于單箱雙室變截面混凝土腹板模型梁。模型梁前二階扭轉自振頻率隨著邊中跨徑比的增加而增加，第三階扭轉自振頻率在邊中跨徑比為0.55后呈下降趨勢。

綜上可知，在實際設計中適當增大單箱雙室變截面波形鋼腹板連續箱梁的邊中跨徑比有助于提高其豎彎和扭轉自振頻率。

4 結論

1）傳統混凝土腹板被波形鋼腹板代替后，與混凝土連續箱梁相比，連續組合箱梁的一階自振頻率減小了12.1%，單箱雙室變截面波形鋼腹板連續組合箱梁高階自振頻率比傳統混凝土腹板連續箱梁小。

2）采用JTG D60—2015《公路橋涵設計通用規范》估算波形鋼腹板連續組合箱梁自振頻率，與試驗值相差約15.7%，而修正公式計算值與試驗值相差約12.3%，修正公式計算值誤差比規范值小3.4%左右，修正公式更合理。

3）設置中支點橫隔板能夠有效改善單箱雙室變截面波形鋼腹板連續箱梁的動力性能，設置中跨和邊跨橫隔板對動力性能影響有限。

4）適當增加邊中跨徑比有助于提高單箱雙室變截面波形鋼腹板連續箱梁前三階自振頻率。