多雷達實時引導數據的自適應加權融合算法研究

霍曾元 昝少東 邱德敏 馮志浩 祝敬樂 于春朋

摘要：針對目前國內地面測控站部署的多套雷達間數據共享實時性差、互引導數據利用率低等不足，為提高雷達互引導數據的精度和可靠性，提出了一種基于數據自適應加權融合算法的多套雷達實時互引導方法。該方法無需統計跟蹤數據的統計特性等先驗信息，直接依據當前時刻測量樣本點進行分析計算，進而自適應分配各測量值權重，達到多組數據融合的目的。經仿真實驗和實際工程驗證，該算法融合效果較好，具有較強的實時性和魯棒性，很大程度提升了雷達互引導功能的實用性。

關鍵詞：實時引導；數據融合；支持度；魯棒性

中圖分類號：TP212.9文獻標志碼：A文章編號：1008-1739（2022）23-55-4

0引言

國內各衛星測控地面站內均部署有多套雷達測量設備，執行空間站等重大任務時，站內多套雷達需同時跟蹤同一飛行器目標。飛行器可見弧段內，各雷達均基于軌道動力學模型事先計算出的理論彈道作為引導數據源，引導雷達捕獲跟蹤目標飛行器。當某套雷達理論彈道數據無效或飛行器偏離預定軌道時，則需要利用其他已經捕獲跟蹤目標的雷達的實時數據引導該雷達重新捕獲跟蹤目標。目前，已開發出雷達互引導軟件，通過將某套雷達的跟蹤原始數據復制遷移的方法初步實現多套雷達間的相互引導，但引導過程中經常出現數據中斷、跳點和引入干擾等問題，導致實際引導效果較差，限制了多雷達互引導技術的應用。因此，如何有效融合多套雷達跟蹤數據，提高融合數據的精度和魯棒性，是提升多雷達互引導技術性能的關鍵。目前數據融合算法取得了很多研究成果，如文獻[1]利用了總均方差最小條件下的拉格朗日定理，求解最優權值；文獻[2-3]利用了模糊理論中的隸屬度函數，調整權值分配，但這些融合算法均要求各測量值的先驗知識和狀態模型，計算量大，前置條件復雜，并不適用于要求引導數據高實時性、高魯棒性的雷達跟蹤系統。

為滿足多雷達互引導技術的需求，本文提出了一種改進的自適應加權融合算法。該算法無需測量數據的各類先驗知識，只針對多套雷達在某一時刻的一組數據進行分析計算，進而確定各套雷達測量數據相應的權重分配。與傳統算法相比，該算法計算量小、流程簡潔，通過算例仿真驗證了本算法具有很強的實時性和魯棒性。

1加權數據融合算法

傳統的多源數據融合以文獻[4]提出的算數平均法和文獻[5-7]提出的最小二乘加權法較為常見。前者直接對測量數據進行算術平均；后者利用了數據源的先驗精度信息，其融合決策結果具有統計意義上的最小方差。2種方法均是對各數據源賦予固定權重，計算量小，實施性強。缺點是當某個數據源數據出現異常（無數據或數據量級異常等）時，往往給出較大偏差甚至錯誤的融合結果。自適應加權算法[8]提高了融合決策的魯棒性，但在生成融合權重時設定了門限值，并利用了二值判定方法，既提高了算法的復雜性也降低了測量值的利用效率。如何兼顧計算的快速性、數據的準確性和策略的穩定性是互引導數據改進工作的重點。

本文從實時性和魯棒性出發，以某測控站內套不同精度雷達的測量數據（ =1，2，…， ）為例，提出一種改進的自適應權值分配策略。

該策略主要包含以下步驟：

將4種算法對方位角度（50°）進行100次采樣，通過Matlab仿真計算，數據融合效果評價如表2所示。

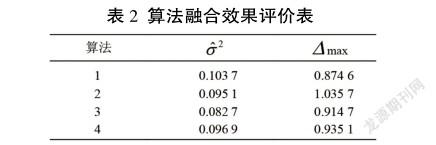
由表2可以看出，總體上，算法1～4融合結果精度較高，效果均表現較好，其中算法4最優，這是由于最小二乘加權融合算法是基于初始跟蹤精度，且融合數據總方差最小的條件下推出的權重分配，而雷達測量數據由Matlab軟件根據初始跟蹤精度仿真生成，這些數據的統計特性與初始設定的跟蹤精度嚴格一致，數據環境吻合度高，融合結果必然方差最小。

為進一步觀察數據融合結果與原始測量數據間的關系，取前10次樣本，4套雷達跟蹤測量值的偏差以及4種算法產生的融合結果如圖1和圖2所示。

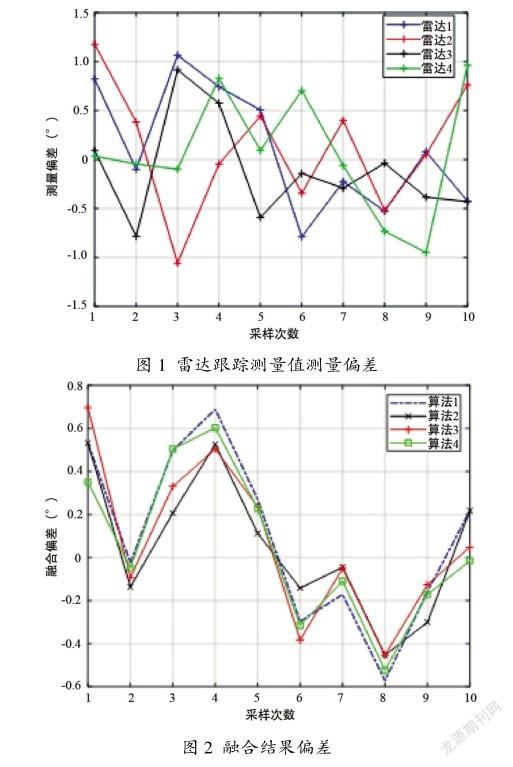
由圖分析可得：

①算法4（即本文算法）與算法1相比，融合偏差更小，趨勢更穩定。

②在第6次采樣中，初始精度最高的雷達1給出的測量值偏差近乎最大，其所占權重最高，故算法3融合效果最差。

③在第4，8次采樣中，測量值分別偏大、偏小，故所有算法融合結果都相應的偏大、偏小。

在目標跟蹤過程中，由于外界干擾及雷達自身裝備特性影響，容易出現部分雷達目標丟失或者設備故障帶來的量測數據精度變差等情況，為比較各算法的魯棒性，給出場景二。

場景二：假設各雷達初始方位跟蹤精度同場景一，但在跟蹤過程中，雷達1設備故障，方位跟蹤精度突然下降至20，將4種算法對方位值（50°）進行100次采樣，通過Matlab仿真計算，數據融合效果評價如表3所示，4種算法產生的融合結果偏差如圖3（取前10次樣本）所示。

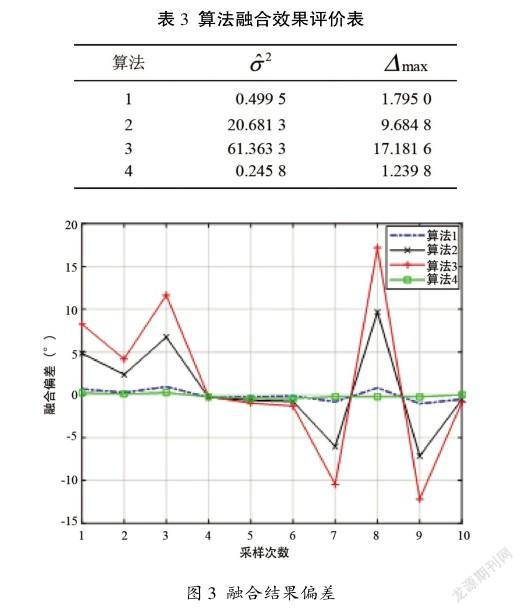
由表3和圖3可以看出：

①算法2和算法3均表現較差，融合結果已不可用，其中算法3將初始精度最高的雷達1量測數據賦予了最高的權重，因此雷達1跟蹤精度變差時，它的融合效果最差，這也驗證了場景一的結論。

②算法1和算法4表現較好，其中算法4融合效果最優，穩定性最好。后經過大量實驗驗證，在單套雷達設備故障，跟蹤測量值精度發散時，算法4融合結果方差仍能維持在0.4左右，而算法1融合結果方差下降至10以下，進一步說明算法4比算法1具有更強的魯棒性。

通過上述2個仿真場景中代表固有權重的算法2和算法3融合效果前后對比，可得初始精度的分析使用可提高數據融合效果，但降低算法的魯棒性。為二者兼顧，文獻[9]對固有權重和測量權重的加權占比系數做了簡單分配。其實系數分配原則需要與實際應用工程相匹配，如本文的互引導數據更強調算法的魯棒性，即互引導數據作為備用數據源，當雷達跟蹤異常時才會啟用。因此算法內權重的組成不需要包含使用初始精度推算的固有權重，即固有權重系數占比為零。當然，實際其他工程中也可以降低算法的部分自適應性，將2個加權占比系數作為開放參數，依據不同應用場景實時調整。

3實測數據驗證

為貼合實際應用場景二，對某地面站內4套雷達（跟蹤精度全部為0.015°）的某一弧段數據進行融合實測，分別用4種算法計算融合彈道。為便于比較融合效果，讓精度最高的雷達測量彈道近似測量真值，擇機選擇另一套雷達，讓其跟蹤測量彈道疊加方位、俯仰均為5°的偏差，各算法融合結果如圖4所示。

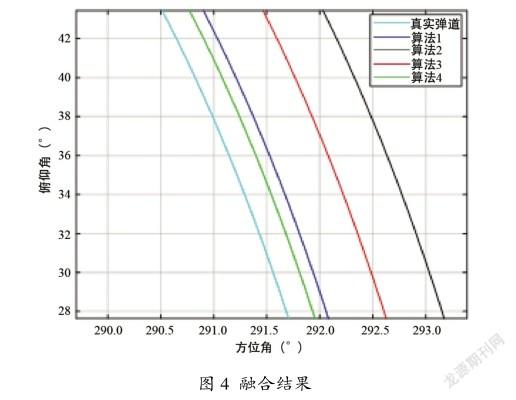
由圖4可以看出，代表本文算法的綠色線條最接近真實軌跡，數據精度最高，融合效果最優。

4結束語

本文從提高地面測控站雷達互引導功能的實用性角度出發，提出了一種改進的自適應加權融合算法。通過系統仿真和實際工程應用，證明該算法在預設場景中雷達出現異常時，可有效避免互引導數據出現斷點、野值等風險，且該算法數據處理的實時性更好，在雷達測量領域具有良好的推廣應用價值。

參考文獻

[1]張陽，沈明霞，孫玉文，等.基于多傳感器自適應加權融合的溫室信息系統[J].傳感器與微系統，2014，33（6）：100-103.

[2] WANG J H， GAO Y. Multi-sensor Data Fusion for Land Vehicle Attitude Estimation Using Fuzzy Expert System[J]. Data Science Journal， 2006（4）： 127-139.

[3]胡振濤，劉先省.基于相對距離的一種多傳感器數據融合方法[J].系統工程與電子技術，2006（2）：196-198.

[4]陳忠德，蔣靜坪.一致性多傳感器數據融合方法的改進[J].傳感器技術， 1995（5）：52-55.

[5]凌林本，李茲剛，陳超英，等.多傳感器數據融合時權的最優分配原則[J].中國慣性技術學報， 2000，8（2）：36-39.

[6]劉建書，李人厚，常宏，等.基于相關性函數和最小二乘的多傳感器數據融合[J].控制與決策， 2006（6）：714-716.

[7]趙華哲，李強，楊家建.基于最小二乘原理多傳感器加權數據融合[J].微型機與應用， 2013， 32（12）：7-10.

[8]邢曉辰，蔡遠文，任江濤，等.一種考慮傳感器精度的數據自適應加權融合算法[J].電訊技術，2015，55（10）：1079-1086.

[9]熊彥銘，李世玲，李軍，等.多傳感器時間控制系統的數據融合新算法[J].彈箭與制導學報， 2012， 32（1）：171-174.