基于矢量控制的帶式輸送機PMSM調制研究

楊京東，杜賢羿，李大偉，吳 康，任麗霜

(山西大同大學 煤炭工程學院,山西 大同 037003)

礦用帶式輸送機是一種方便快捷的礦山物料運輸設備。由于帶式輸送機可長距離、連續性的運輸大量礦用物料等諸多優點，被廣泛應用于采區的上下區段處和平巷地區，以及運輸口的大巷處與井口運輸的過道走廊等地[1]。隨著煤炭需求量日益增大，生產效率得到大幅度提高，礦用帶式輸送機正逐步向著高端化、大型化、高速化發展。帶式輸送機作為礦用關鍵設備之一，一旦有故障發生，會導致大量物料停滯中途而無法運輸，與它相關的一些設備會產生連鎖反應從而受到影響，可能會造成生產停止或者人員傷亡等重大事故。[2]由此可見，礦用帶式輸送機作為運輸系統的中樞環節，地位極其重要，一旦出現故障將會是不可逆轉的，并且可能會發生重大事故。所以，在礦山生產作業時確保它的正常運行是十分重要的。礦用帶式輸送機的驅動依賴于電機，因此控制電機的穩定是其安全運行的重點。

由于交流電機可直接連接變壓器獲得交流電能，在早期的牽引系統中，往往是采用交流電機進行驅動的[3]。隨著電機技術和變頻器的快速發展，均給永磁同步電機(PMSM)在煤礦井下的應用創造了有利條件。較之傳統的生產設備，永磁同步電機具有諸多應用優勢，如：可實現智能控制，并且安全可靠、高效節能、噪音污染小和便于檢修維護等[4]。近年來，永磁同步電機逐漸在煤礦生產中得到了廣泛應用，尤其是在帶式輸送機中起到了舉足輕重的作用。

以往在PMSM驅動系統中檢測電機轉速，多采用機械式傳感器進行檢測，以實現驅動系統對PMSM的控制要求。由于采用機械式傳感器容易受到機械運行時的沖壓、震蕩等不利因素影響，且安裝在電機附近容易受電機的溫升影響，使輸出信號可靠性降低，影響整個系統的穩定性[5]。

為了盡可能解決這一問題，多年來研究人員通過研究電機的數學模型，發現電機數學模型中電壓電流與轉子角速度存在一定的聯系，即通過檢測電機的電壓、電流值，經過理論推導可以得到轉子位置和轉速信息，從而代替了機械式速度檢測傳感器，減少了系統的附加設備，大大增加了對電機驅動系統速度檢測的可靠性，減小了系統的日常維護量[6]。因此，研究三相PMSM調速系統對煤礦井下帶式輸送機的高效性和安全性具有重要的意義。

1 三相PMSM的基本數學模型

建立PMSM數學模型，要假定以下條件[7]：一是不計電機磁飽和；二是忽略電機磁滯損耗；三是轉子無阻尼繞組。

PMSM在三相靜止坐標系下的電壓方程為

(1)

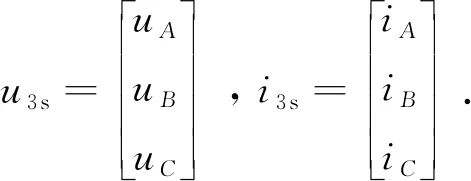
磁鏈方程為

ψ3s=L3si3s+ψf·F3s(θe).

(2)

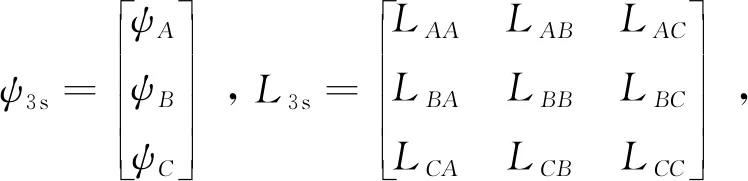
式中：LAA、LBB、LCC分別為三相定子繞組的自感；LAB、LBA、LAC、LCA、LBC、LCB分別為繞組間的互感。

電磁轉矩方程為

(3)

式中：θm為機械角；pn為三相PMSM的極對數。

由式(2)和式(3)可知，PMSM在三相靜止坐標系下的數學模型具有強耦合、多變量的性質，因此需要通過坐標變換將PMSM的數學模型簡化。

2 坐標變換

圖1為各坐標系之間的關系，ABC為自然坐標系，α-β為靜止坐標系，d-q為同步旋轉坐標系。

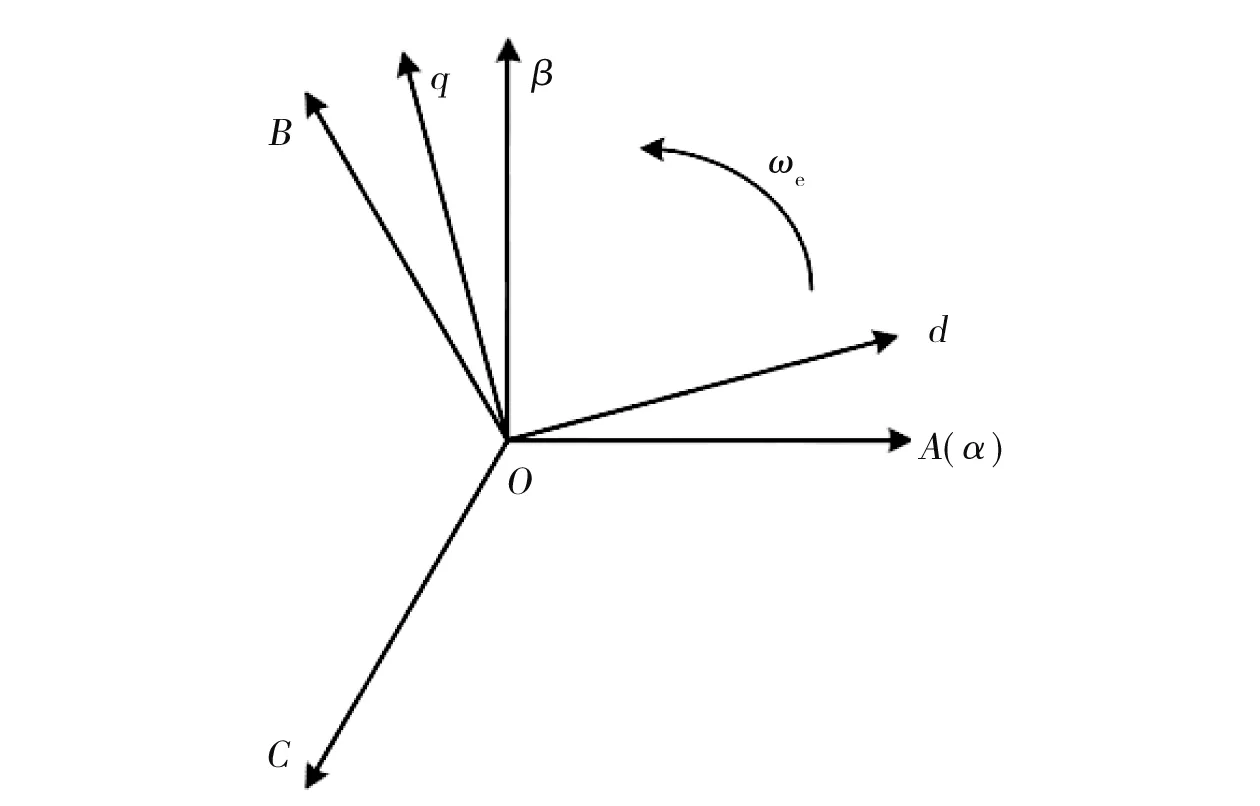
圖1 各坐標系之間的關系

2.1 Clark變換

將自然坐標系ABC變換到靜止坐標系α-β的坐標變換為Clark變換，可以得出如式(4)所示的坐標變換公式：

[fαfβ]T=T3s/2r[fAfBfC]T.

(4)

式中：f代表電機的電壓、電流或磁鏈等變量；T3s/2s為坐標變換矩陣，采用幅值不變約束條件，可表示為

(5)

2.2 Park變換

將靜止坐標系α-β變換到同步旋轉坐標系d-q的坐標變換稱為Park變換，可以得出如式(6)所示的坐標變換公式：

[fdfq]T=T2s/2r[fαfβ]T.

(6)

式中：T2s/2r為坐標變換矩陣，可表示為

(7)

2.3 反Park變換

將同步旋轉坐標系d-q變換到靜止坐標系α-β的坐標變換稱為反Park變換，可以得出如式(8)所示的坐標變換公式：

[fαfβ]T=T2r/2s[fdfq]T.

(8)

其中：T2s/2r為坐標變換矩陣，可表示為

(9)

3 三相電壓源逆變器PWM技術

電壓源逆變器PWM技術在電機的驅動系統中尤為重要，目前常用的PWM技術主要為正弦脈寬調制(SPWM)和空間矢量脈寬調制(SVPWM)技術。SPWM技術的控制思想是設法將直流母線電轉變為正弦波的電流，一般通過比較三角載波和正弦調制波來生成PWM，然后再控制IGBT的高頻通來實現正弦波的電流。而SVPWM技術是由SPWM技術應用改進而來，其工作原理是:基于跟蹤圓形旋轉磁場的原理，對IGBT的6個控制開關進行規律控制，從而使產生8種基本的空間矢量，再將矢量轉換成調制波，使電機產生恒定的轉矩[8]。

相較于SPWM技術，SVPWM技術對電壓的利用率更高、開關損耗更低。SVPWM自首次提出以來，由于其性能優良，受電機領域的許多研究者追捧，爭相對其開展研究應用。

圖2中的三相逆變電路通過SVPWM技術輸出的調制波，對6個功率開關管(VT1-VT6)進行規律控制，控制其接通和閉合的時間,控制其接通的順序，從而使三相逆變電路輸出能使PMSM高性能控制的交流電。

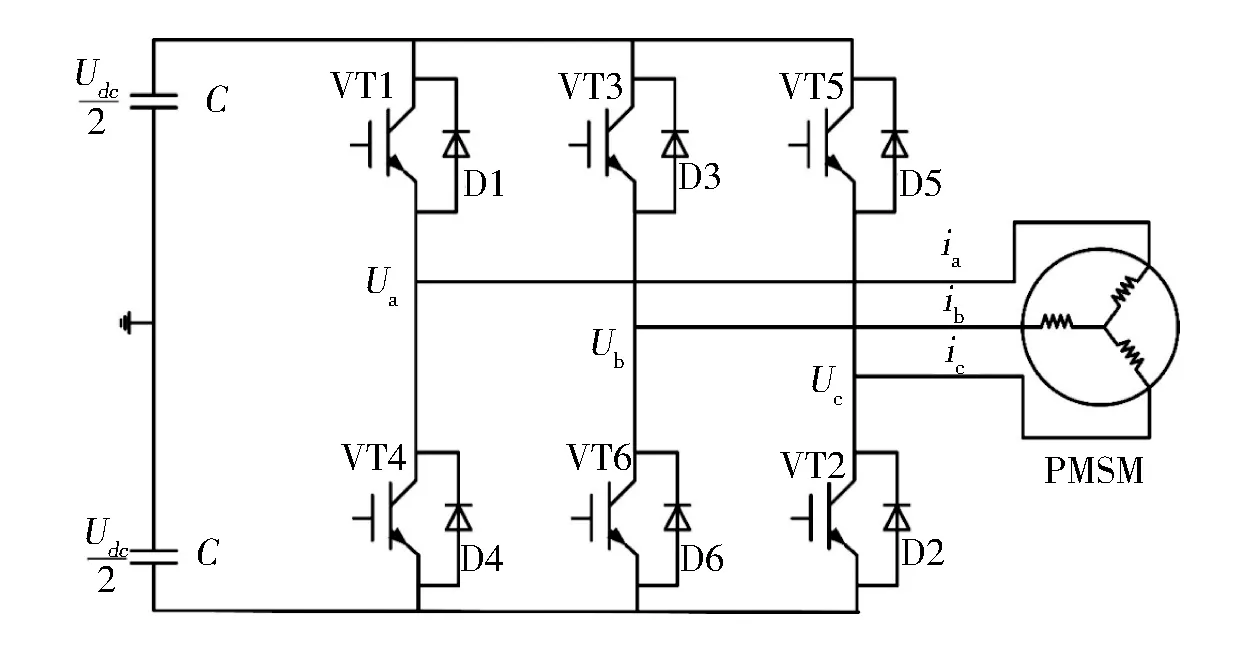
圖2 PMSM的逆變電路

圖2中，Ua、Ub、Uc分別為逆變器輸出的相電壓；Udc為直流母線電壓。

根據開關狀態a、b、c對于0和1的選擇，可以組合成逆變器的6種開關狀態，這6種開關狀態可等分地將正六邊形劃分為6個扇區，每個狀態占用一個扇區。正六邊形中的圓是磁鏈的目標軌跡。SVPWM空間矢量如圖3所示。

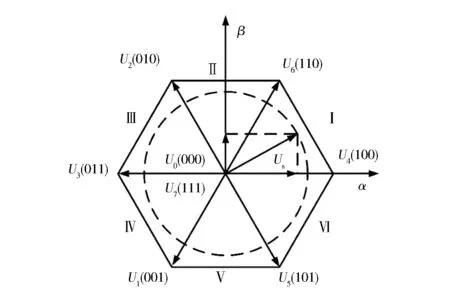
圖3 空間矢量圖

3.1 參考電壓扇區判斷

用uα和uβ表示參考電壓Uref在α、β軸上的分量，定義Uref1、Uref2和Uref3三個變量，令

(10)

再定義3個變量A、B、C，可知：

若Uref1>0，則A=1，否則A=0；

若Uref2>0，則B=1，否則B=0；

若Uref3>0，則C=1，否則C=0。

令N=A+2B+4C，可得N與扇區的關系如表1所示：

表1 N與扇區的對應關系

3.2 計算作用時間

根據式(10)對電壓空間矢量幾何分析和圖3的電壓空間矢量圖可以得到如下關系式：

(11)

式中:t1、t2分別為扇區1、2內的作用時間。對其化簡得：

(12)

根據以上對特定扇區的時間計算原理，可以知道其他扇區的時間計算。X、Y、Z做為所設中間變量如下式：

(13)

表2為各個扇區t0(t7)、t4和t6作用的時間。

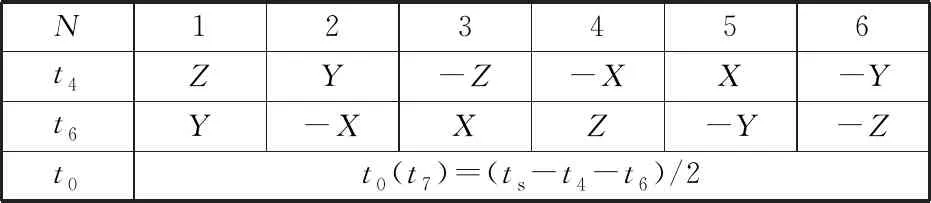
表2 各扇區作用時間t0(t7)、t4和t6

如果t4+t6>ts，則需要進行過調制處理，令

(14)

3.3 扇區矢量切換點的確定

首先定義

(15)

則三相電壓開關時間切換點tcm1、tcm2和tcm3與各扇區的關系如表3所列。

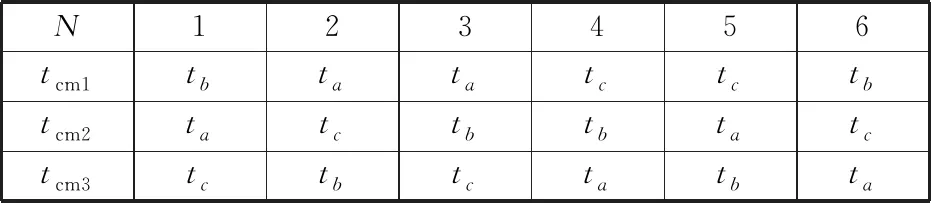
表3 各扇區時間切換點tcm1、tcm2和tcm3

經過以上三個步驟，只需再添加合適頻率的三角載波信號即可輸出脈沖信號。

4 三相PMSM的矢量控制

矢量控制技術是通過對電機定子電流在同步旋轉坐標系中大小和方向的控制，達到對直軸和交軸分量的解耦目的。三相PMSM矢量控制系統是一個多環控制系統，由轉速外環和電流內環構成，其構成的開環傳遞函數并不是典型的系統，一般可以采用PI調節器，將電流內環校正為典型Ⅰ型系統，其作用是使PMSM的定子電流與設定電流盡量吻合，減小估計誤差；將轉速外環校正為典型Ⅱ型系統，其作用是控制電機的轉速，使其能夠達到既能調速又能穩速的目的，提高了其抗干擾能力[9]。

4.1 PMSM的PI電流內環控制

矢量控制系統中，電流環是對iq、id進行控制，進而控制電機轉矩[10]。由于PMSM的磁通完全由永磁體來提供，當id=0時，PMSM無直軸的電樞反應，只需控制交軸電流值即可控制電機轉矩，實現PMSM的靜態解耦。

由于id=0，分析q軸電流環即可，結構框圖如圖4所示：

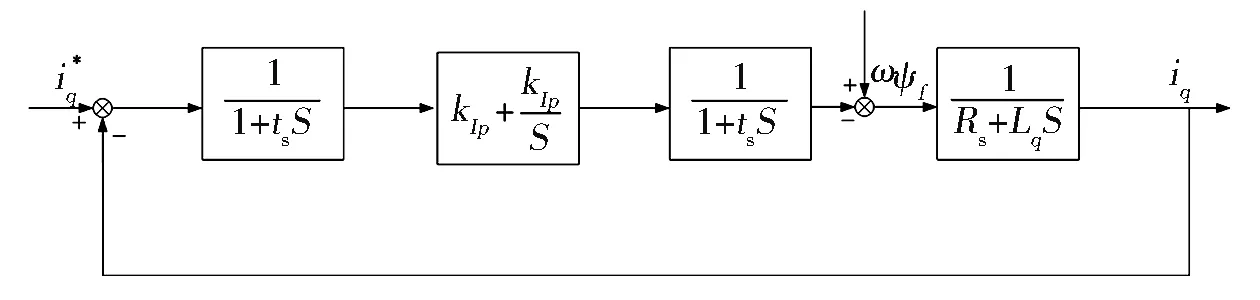
圖4 電流調節器PI控制動態框圖

分析圖4可得零極點形式的傳遞函數是：

(16)

為了簡化分析，合并電流采樣周期模塊，并忽略ωΨf的擾動，如圖5所示。

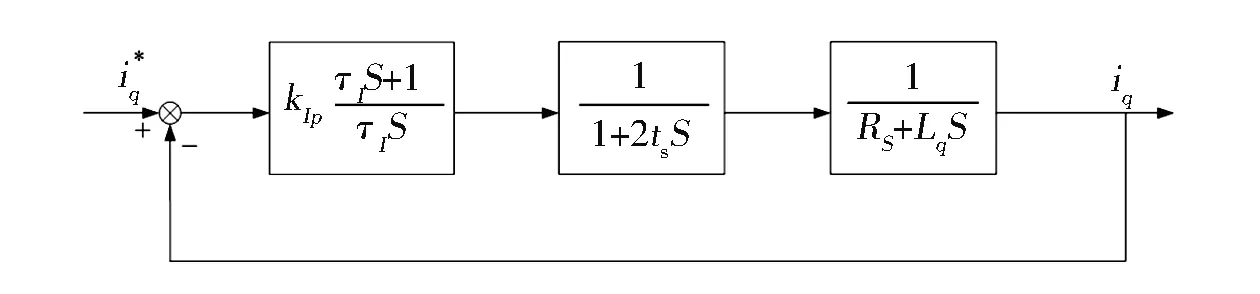
圖5 電流調節器PI控制簡化動態框圖

開環傳遞函數校正后可得：

(17)

由式(17)知閉環傳遞函數：

(18)

受開關頻率較高的影響，s2的系數通常可忽略，即得簡化后的閉環傳遞函數：

(19)

考慮調節時間、響應速度和超調量的綜合因素，若想得最優值，需設定阻尼比ξ=0.707，可得：

(20)

由式19和式20可推出電流環的PI參數為：

(21)

4.2 PMSM的PI轉速外環控制

圖6為轉速調節器PI 控制動態框圖。

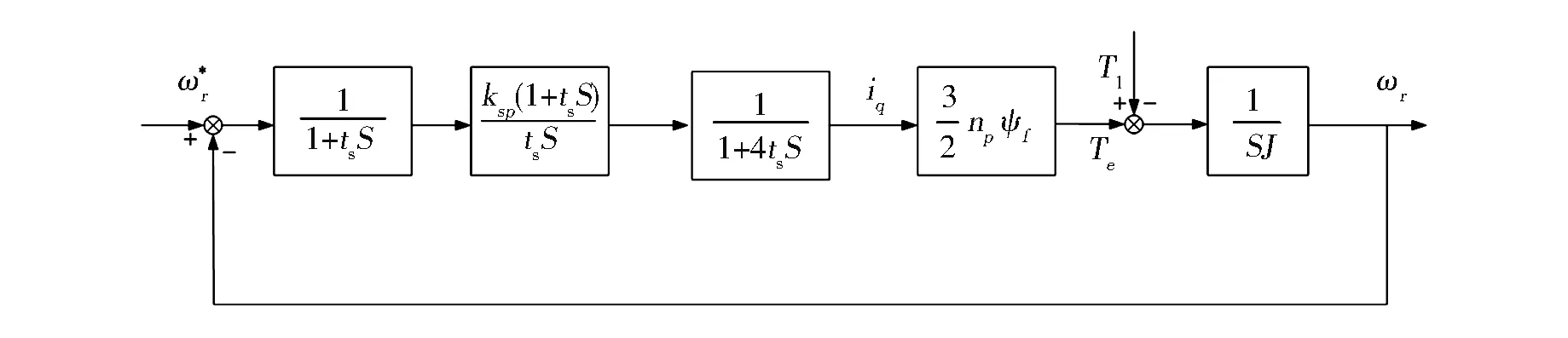
圖6 轉速調節器PI控制動態框圖

先忽略負載轉矩Tl，并將電流內環等效為小時間常數4ts與速度信號采樣的小時間常數ts進行合并得tes=5ts，簡化圖如圖7所示：

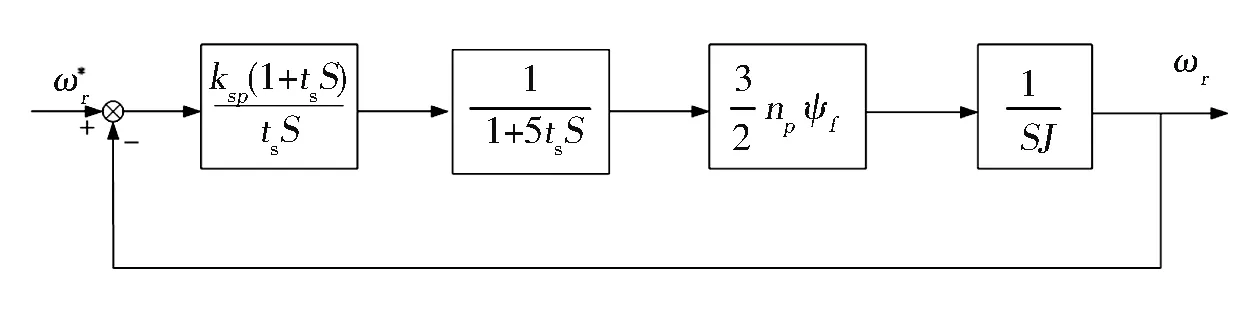
圖7 轉速調節器PI控制簡化動態框圖

由圖7可知開環傳遞函數為：

(22)

通過典型Ⅱ型系統可整定為：

(23)

(24)

即可推出轉速外環的PI參數為：

(25)

5 三相PMSM系統的建模與仿真

根據以上分析過程，建立三相PMSM調速系統仿真模型，如圖8所示。設定電機初始轉速為1 500 r/min，并在0.5 s時突加負載轉矩TL=10 N·m。

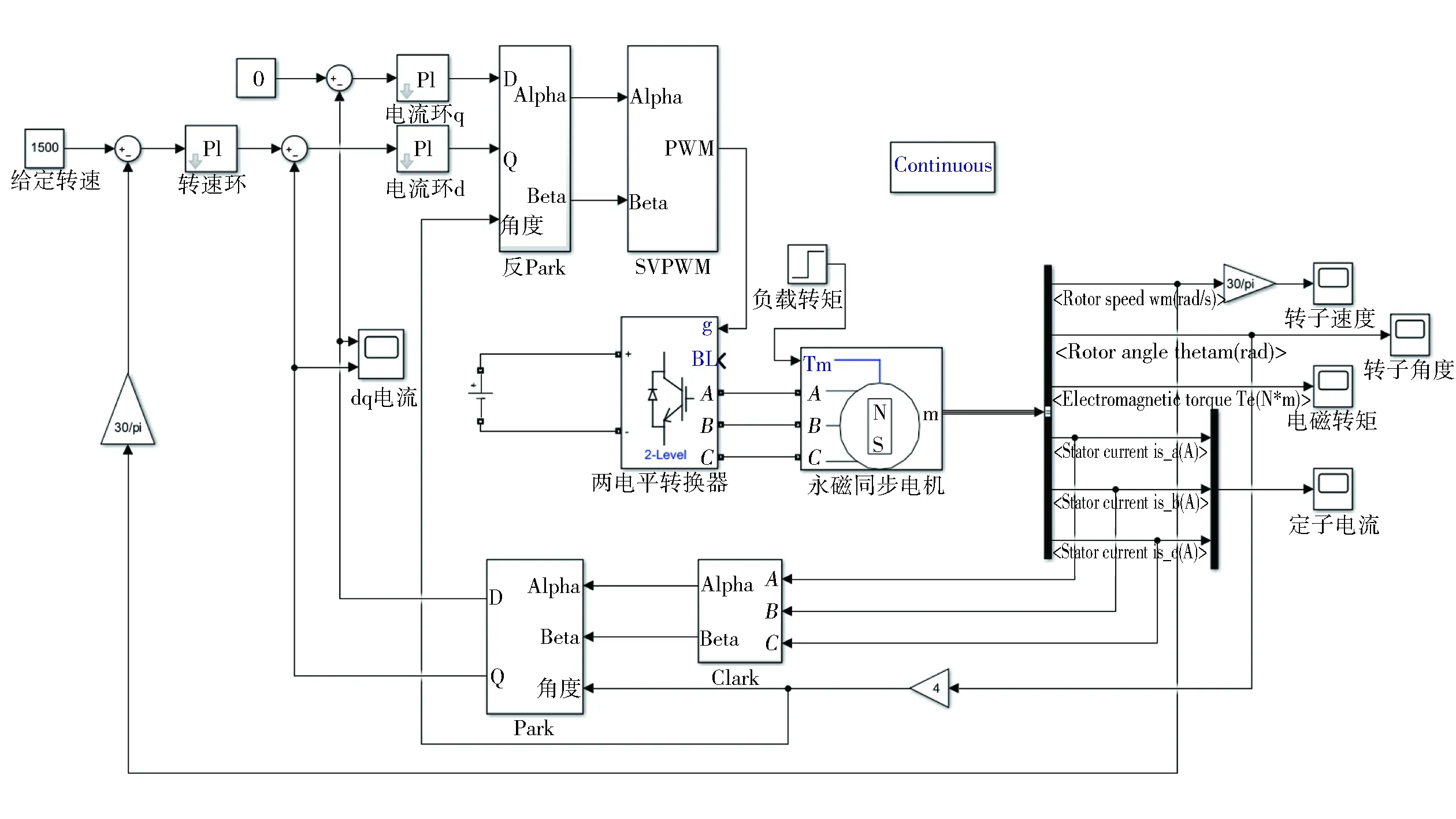
圖8 三相PMSM調速系統仿真模型

5.1 坐標變換的建模

由式(5)可建立如圖9所示的Clark變換模型，由式(7)可建立如圖10所示的Park變換模型，由式(9)可建立如圖11所示的反Park變換模型。

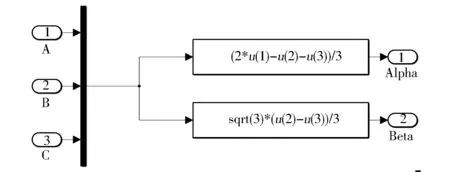
圖9 Clark變換

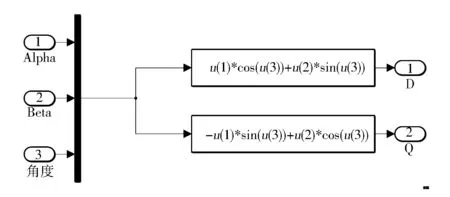
圖10 Park變換

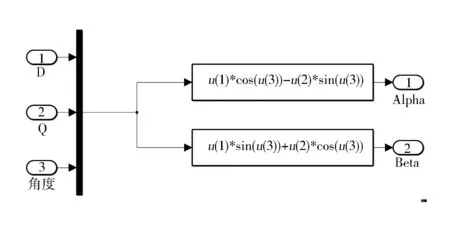
圖11 反Park變換

5.2 SVPWM算法的建模

圖12所示為SVPWM算法的仿真模塊圖。PWM開關周期Tpwm=1/6 000，直流側電壓Udc=560 V。由式(10)可建立如圖13所示的扇區N的判斷模型，由式(13)可建立如圖14所示的中間變量X、Y和Z的計算模型，由式(14)可建立如圖15所示的T4(T1)和T6(T2)的計算模型，由式(15)可建立如圖16所示的切換時間tcm1、tcm2和tcm3的計算模型。

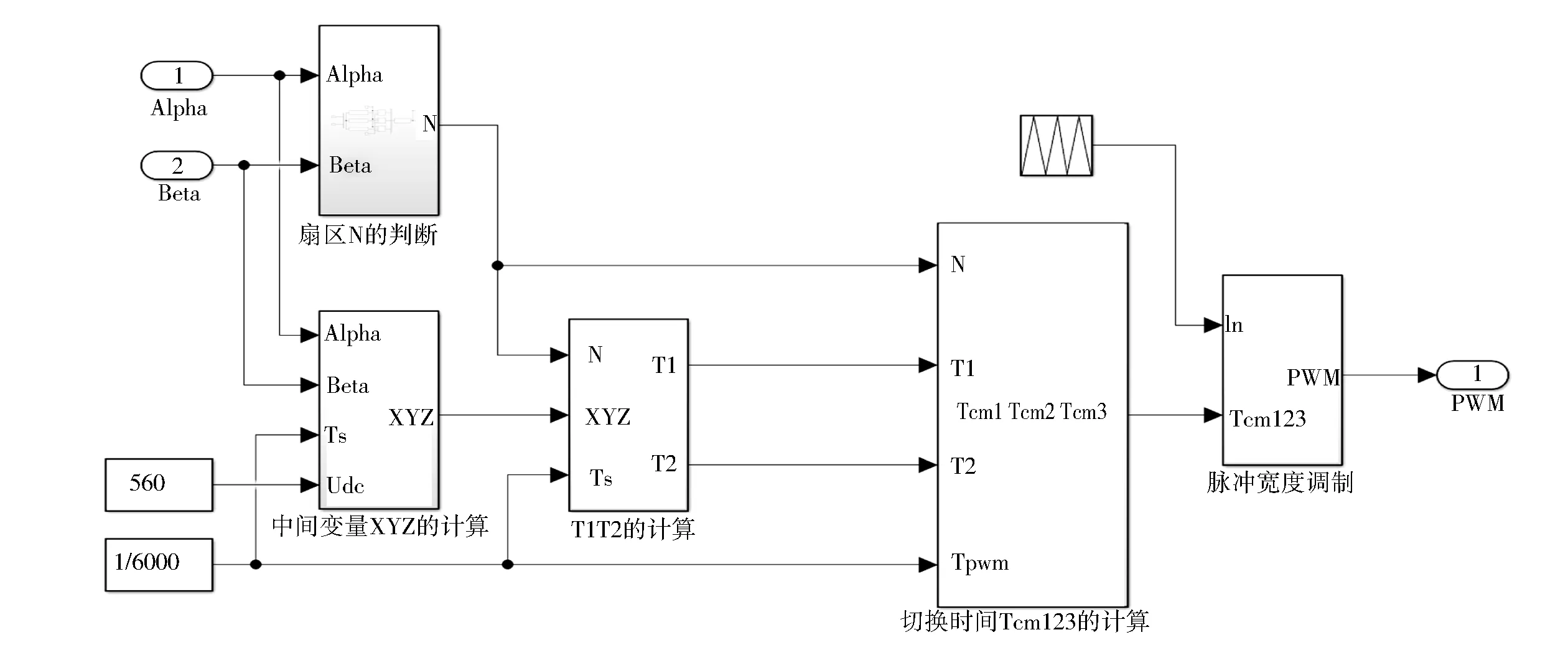
圖12 SVPWM模塊

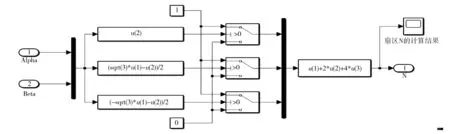
圖13 扇區N的判斷

圖14 計算X、Y和Z

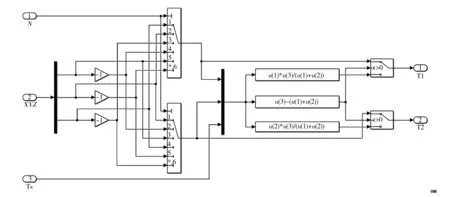
圖15 t4(t1)和t6(t2)的計算

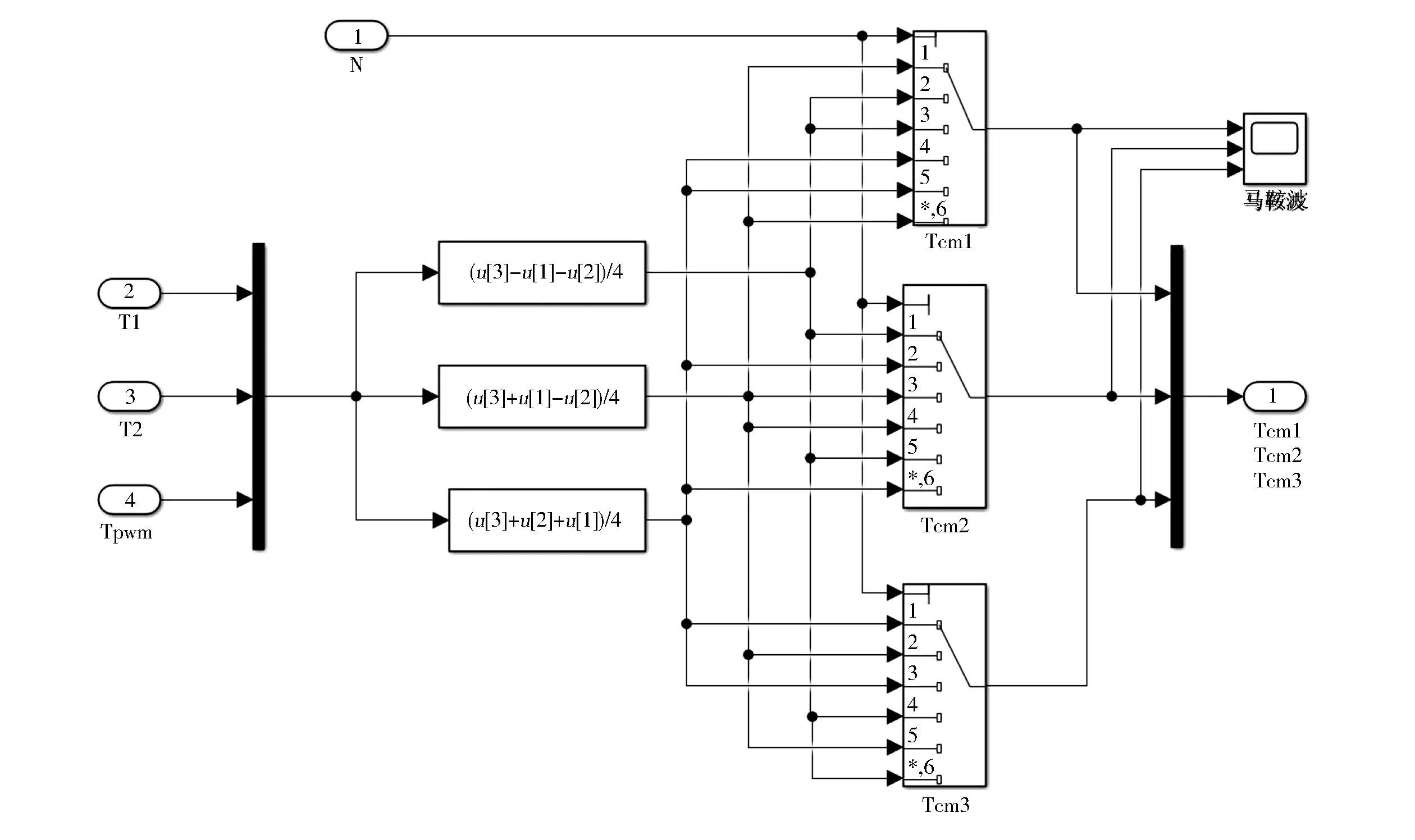
圖16 切換時間的計算

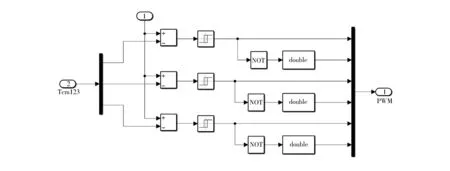
圖17 脈沖寬度調制輸出

5.3 仿真結果

由圖18可知，扇區N值呈現為交替變換的特點，與表1所示的結果相同。圖19所示的調制波形呈馬鞍形，即提高了母線電壓利用率，增強了PMSM的動態響應。由圖20可知，PMSM以較快的響應速度上升到設定轉速值，且僅有很小的超調量；在0.5 s時，PMSM產生波動并在0.05 s內恢復到穩定值。結果表明,PMSM轉速可以較好地跟隨系統設定值，轉速上升時間短，跟蹤速度快，超調量較小，只在負載轉矩突變時產生較小波動，三相正弦電流和電磁轉矩都具有較好的動態響應性能。從而說明所設計的PMSM系統模型具有較好的動態性能和抗擾動能力，符合礦用帶式輸送機對PMSM的控制要求。

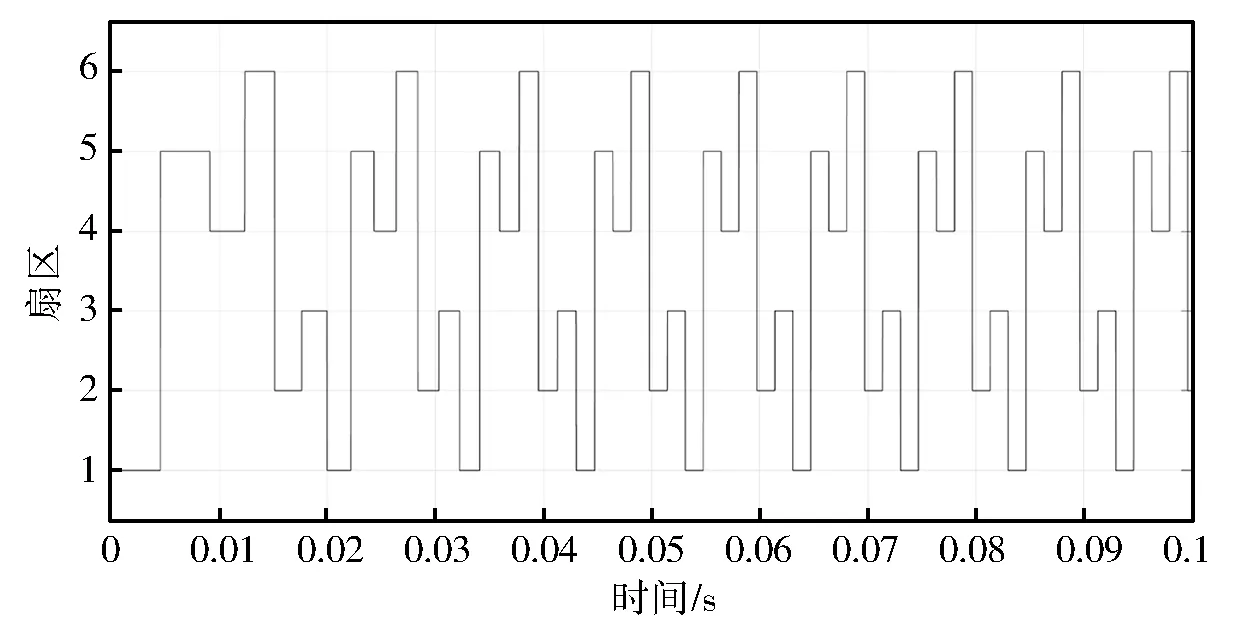
圖18 扇區N的計算結果

圖19 切換時間tcm1、tcm2和tcm3的計算結果

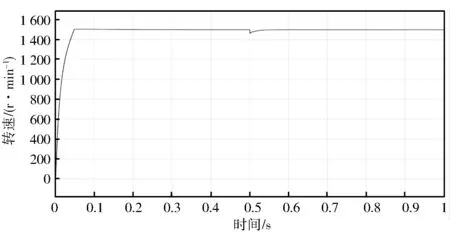
圖20 轉速nr的變化曲線

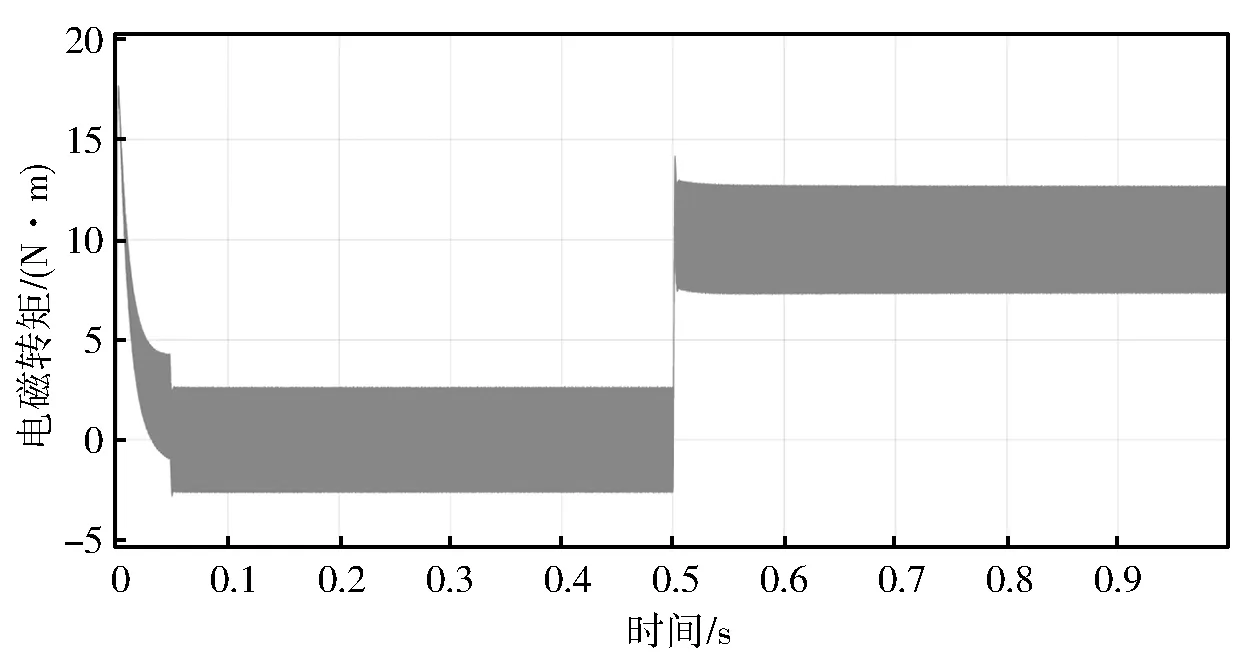
圖21 電磁轉矩Te的變化曲線

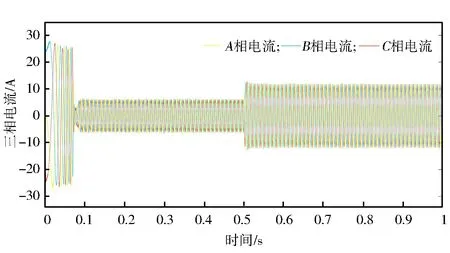
圖22 三相電流的變化曲線

6 結語

由于PMSM具有啟動轉矩大、體積小和高效節能等優點，很快被大量應用在各個制造業領域。本文以礦用帶式輸送機系統PMSM為研究對象，選用的調速系統控制方案為基于矢量控制技術和SVPWM的三相PMSM調速系統。對矢量控制技術和SVPWM的控制原理做了詳細的介紹，并在MATLAB/Simulink中搭建仿真模塊進行實驗。結果表明,在基于矢量控制技術和SVPWM的三相PMSM調速系統具有快速準確、效率高和抗擾動能力強的優點。證實了PMSM在煤礦井下帶式輸送機的應用中,能夠極大地提高生產效率和提升煤礦生產的安全性。因此PMSM控制系統必將隨著現代工業技術的發展，在煤礦井下的應用開拓更加廣闊的發展空間。