基于CGSOA-BPNN優化AlCoCrNiFe高熵合金涂層等離子噴涂工藝參數

李贊，張長勝，馬濤，王卓

基于CGSOA-BPNN優化AlCoCrNiFe高熵合金涂層等離子噴涂工藝參數

李贊a，張長勝a，馬濤b，王卓a

（昆明理工大學 a.信息工程與自動化學院 b.材料科學與工程學院，昆明 650093）

解決等離子噴涂工藝參數耦合導致的參數選取困難問題，提高AlCoCrNiFe高熵合金涂層力學性能。提出全局混沌高斯融合的海鷗算法（CGSOA），優化權值和閾值，使BP（Back Propagation, 反向傳遞）神經網絡訓練輸出理想控制參數。利用改進logistic混沌序列實現網絡參數初始化種群的全局搜索，提高權值和閾值初始質量。引入改進logistic映射跳出局部最優，通過加強局部搜索能力，以提高算法收斂精度。引入高斯變異增加種群多樣性，提高全局搜索能力。選取6個基準函數，對BAS、PSO、ACO、SOA及CGSOA算法進行測試，仿真結果表明，所提算法具有較快收斂速度、較高尋優精度和穩定性。CGSOA算法優化BP神經網絡得出最佳控制量為：噴涂距離99.7 mm，噴涂電流649.6 A，噴涂電壓56.3 V，送粉載氣203.1 L/h，送粉電壓5.1 V。以其進行噴涂試驗，涂層結合強度和顯微硬度分別為25.2 MPa和616.8HV，與模型預測值的相對誤差分別為3.02%和2.91%，驗證了CGSOA-BPNN應用到實際噴涂過程的可行性。CGSOA-BPNN對AlCoCrNiFe高熵合金涂層等離子噴涂工藝參數進行優化，進而提高涂層力學性能，具有一定的現實指導意義。

等離子噴涂；高熵合金涂層；工藝參數優化；BP神經網絡；海鷗優化算法；改進logistic混沌；高斯變異

由于基體與陶瓷層熱膨脹系數相差較大，大氣等離子噴涂過程中會產生較大的熱應力，導致二者粘結性降低，加速涂層失效，故選用一種熱膨脹系數介于二者的金屬合金作為粘結層，降低陶瓷層內部的熱應力，可延長涂層的服役壽命[1]。高熵合金由于其組成元素之間的相互作用而具有高強度、高斷裂韌性、高硬度、高耐磨等優異性能[2-3]。AlCoCrNiFe作為一種典型的高熵合金體系，目前已被制成涂層用于各研究領域，有望成為一種產業化應用的高性能涂層材料[4]。

傳統試錯法在選擇熱噴涂工藝參數以提升涂層性能方面，具有周期長、成本高等缺點[5]。近年來，隨著AI技術的發展，神經網絡逐漸應用到參數優化[6-7]、質量預測[8-9]、材料配方預測[5]等材料噴涂工藝的研究領域。BECKER等[10]利用人工神經網絡對碳化鉻二元涂層的抗空蝕和漿體磨損性能進行建模預測，縮短了試驗時間，降低了成本，但模型的預測誤差較大。針對噴涂過程中呈現出的復雜性和非線性，PATURI等[11]對表面涂層工藝進行建模與參數優化，預測基體表面形成更好沉積涂層的條件，但輸入參數較多而影響收斂速度。HUEN等[12]建立熱噴涂涂層的納米力學性能預測模型，提出一種材料應力應變彈塑性參數分析的新方法，但單一神經網絡易過早收斂，導致預測精度不高。LIU等[13]分析HVOF噴涂工藝參數與涂層性能之間的關系，并且首次引入MIV分析評價熱噴涂過程中人工神經網絡模型輸入變量的重要性，該模型預測的準確性和可靠性較好，但也存在因神經網絡陷入局部問題，而導致預測誤差波動大的缺陷。ZHU等[14]利用卷積神經網絡（CNN），預測了大氣等離子噴涂中飛行粒子的控制參數，大大節約了計算資源和降低了時間成本，但因數據量少使CNN模型過擬合，導致預測效果不佳。綜上所述，在對材料涂層性能的研究分析中，神經網絡作為一種新的工具，代替傳統數值分析、數學模型等方法對材料進行研究，加速了材料科學領域的發展，但單一神經網絡建立的模型擬合度高，對非線性、多輸入多輸出等復雜系統，存在收斂速度慢、精度不高、預測誤差波動較大等問題。

為解決以上缺陷，除充分利用神經網絡優勢外，還需要將群智能優化算法與神經網絡結合，以提高模型的分析能力和精度。在涂層工藝參數優化過程中，以BP神經網絡建立的模型為基礎，將遺傳算法[15-17]（Genetic Algorithm，GA）及粒子群算法[18]（Particle Swarm Optimization，PSO）加入到工藝參數優化模型中，相比于單一神經網絡建立的模型，多工藝參數優化效果較好，優化性能明顯提高，但遺傳算法和粒子群算法在迭代過程中，容易出現陷入局部最優及收斂過早等問題，導致預測誤差過大。為了更好地利用群智能算法，還需要在其基礎上對群智能算法進行改進，以解決此弊端。為了解決群智能算法陷入局部最優，避免“早熟”現象，許多學者對標準算法進行改進。帥茂杭等[19]對骨干粒子群的位置采用搜索權值非線性遞減策略進行位置更新，并對不同搜索階段的最差粒子進行位置更新，以平衡算法全局和局部的搜索能力，提出改進多目標骨干粒子群優化算法，降低了陷入局部最優的概率，從而增加了種群多樣性。張強等[20]將多策略進化概率變異方式引入到人工蜂群優化算法中，避免了陷入局部最優解。馬小陸等[21]在蟻群算法中引入勢場合力遞減系數，避免了勢場蟻群算法因勢場而陷入局部最優的問題。柳長源等[22]在螢火蟲算法中提出一種驅散機制，同時對進化過程中的螢火蟲種群引入變異操作，解決了優化精度不高和容易陷入局部最優的問題。崔雪婷等[23]將改進logistic映射引入蝙蝠優化算法，提出全局混沌蝙蝠優化算法，豐富了種群，有效避免了算法早熟，提高了算法的全局搜索能力。湯安迪等[24]利用cubic映射初始化種群，并融入正余弦算法，提出混沌多精英鯨魚優化算法，克服了算法陷入局部最優的缺點，同時增加了種群多樣性。ZHANG等[25]在麻雀算法中引入logistic映射、自適應超參數和變異算子，提出混沌麻雀搜索算法，克服了迭代后期容易陷入局部最優的缺陷。

海鷗優化算法（Seagull Optimization Algorithm，SOA）是DHIMAN等[26]在2018年提出的新型生物啟發式智能算法，其算法具有探索和開發能力較強、收斂速度快、精度高、魯棒性強、適應性好及調參少等優點。然而，SOA算法也面臨著和其他群智能算法一樣的不足，在搜索接近最優解時，容易“早熟”，陷入局部最優和種群多樣性減少等問題。針對SOA算法收斂性能低、偶爾早熟收斂等問題，CAO等[27]和LEI等[28]將levy隨機游走機制加入算法中，緩解了算法早熟收斂問題。雖然在一定程度上改善了陷入局部最優解問題，提高了勘探和開發的能力，但是依然存在搜索精度不高、收斂精度不足和種群多樣性減少等問題。

所以，針對標準海鷗優化算法的不足，提出一種全局混沌高斯融合的海鷗優化算法（Seagull Optimization Algorithm based on global Chaos and Gaussian fusion, CGSOA），利用CGSOA算法對6個基準函數進行仿真驗證，結果表明，CGSOA算法克服了陷入局部最優問題，收斂速度和精度明顯提高，具有更高的尋優精度和穩定性，證明了該算法具有一定的有效性。在大氣等離子噴涂實驗中，影響AlCoCrNiFe涂層性能的因素有噴涂距離、噴涂電壓、噴涂電流、送粉載氣、送粉電壓等，由于各影響因素間耦合導致噴涂工藝參數難選取，從而對結合強度、顯微硬度等涂層性能具有一定影響。本文將CGSOA算法加入到以BP神經網絡建立的模型上，進行最佳工藝參數尋優，解決參數選取困難問題，使AlCoCrNiFe涂層性能達到更優水平。該模型具有一定的自適應性和較好的魯棒性。

1 海鷗優化算法仿生原理

海鷗在遷移過程中，成群結隊飛行，為避免碰撞，每只海鷗的初始位置不同，海鷗朝著更適應生存的方向前進，其他海鷗根據更適應生存的海鷗路徑來更新它們的初始位置。海鷗攻擊海面上的獵物時，做出螺旋形狀的運動，鎖定并對其獵物發動攻擊，獵物所在位置為最優位置，此時的適應度值最優。海鷗優化算法主要由遷徙和攻擊行為組成，利用海鷗的遷徙行為進行全局搜索，利用攻擊行為進行局部搜索，如圖1所示。海鷗優化算法的主要步驟包含遷移和攻擊。

圖1 海鷗遷移和攻擊行為

1.1 遷移

海鷗遷移是一個含勘測的多元化全局搜索過程，需滿足以下條件。

條件1：為避免碰撞，需加入變量因子計算海鷗的新位置()，如式(1)、式(2)所示。

式(1)中：=2；控制變量的頻率從2線性遞減到0；為當前迭代次數，maxGen為最大迭代次數。式(2)中：為海鷗的初始化位置，()為第代海鷗所在位置。

條件2：在條件1的基礎上，海鷗朝著更佳適合生存的位置()方向移動，如式(3)、式(4)所示。

式(3)中：為平衡全局勘探和局部開發的平衡因子；rand為（0,1）之間的隨機數。式(4)中：_best為當前最佳適應度值的位置。

條件3：在條件1和條件2的基礎上，海鷗遷移到達新位置()，如式(5)所示。

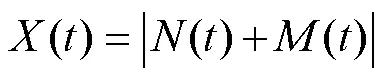
1.2 攻擊

海鷗在遷徙過程中，當發現獵物時，會不斷地調整角度和速度，以螺旋形狀的運動方式攻擊獵物。在攻擊捕食過程中，不斷調整、、三個平面上的運動軌跡方程，如式(6)所示。

式中：為螺旋運動的半徑；和為常數，通常為1；e為自然對數底數；為[0,2π]之間的隨機數。根據式(5)和(6)計算得到海鷗的攻擊位置_()，如式(7)所示。

2 CGSOA算法

改進logistic混沌具有均勻性和遍歷性等特性，用其初始化海鷗種群，增加種群多樣性的同時，可提高初始解的質量，達到全局搜索的目的。引入改進logistic混沌和高斯變異，以更新位置幫助算法跳出局部最優解，可加快收斂速度，提高收斂精度，平衡開發和探索能力，同時也增加了種群多樣性。

2.1 改進logistic混沌

混沌是一種具有非線性、遍歷性、隨機性等特性的運動，對初始條件和參數極為敏感。比較常用的混沌映射方法有sine映射、tent映射和logistic映射，本文采用的是logistic映射。logistic映射[29]產生混沌序列的數學表達式如式(8)所示，當=4時，標準logistic映射產生的混沌量分布不均勻，而且在搜索空間變大之后，logistic混沌優化的時間復雜度會變大，尋優效率會降低[30]。為了解決這個問題，本文提出一種新的logistic映射，改進后的logistic映射的數學表達式如式(9)所示。

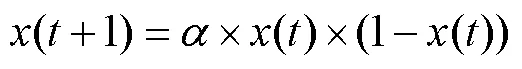
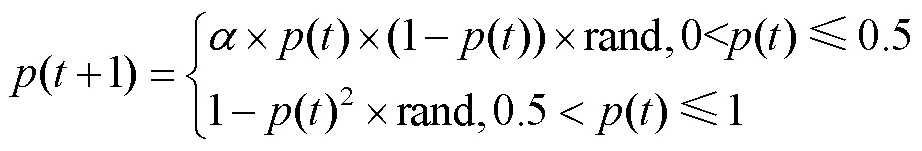
當=4時，迭代2000次，標準logistic和改進logistic的混沌序列分布圖及直方圖如圖2所示。由圖2a和圖2c可以看出，標準logistic混沌絕大部分映射在[0.9,1]之間，超出映射到其他范圍段內數量的3倍左右，顯得較不均勻；相反，由圖2b和圖2d可看出，改進后的logistic混沌映射到每個范圍段的數量相對均勻。由此可知，改進后的logistic混沌的遍歷性及均勻性明顯優于常規logistic，這不僅保證了該混沌的結構屬性，還保留了混沌特性的遍歷性。本文將改進logistic映射產生的混沌序列作為海鷗種群的初始解，保證了初始解的均勻性和遍歷性，提高了種群初始解的質量，加強了全局搜索的能力。

通過式(10)將式(9)產生的混沌序列映射到[,]，作為海鷗優化算法的初始解()。

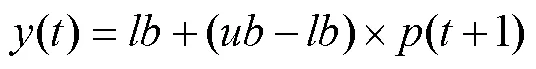
為了避免“早熟”現象，提高局部搜索能力和收斂精度，在當前最優位置引入改進logistic混沌映射，按式(11)對當前最優個體進行混沌產生新解P′(t)。

引入混沌理論完成兩個目標：1）利用改進logistic混沌映射生成混沌序列作為初始解，提高算法初始解質量，在搜索階段保持了較好的協調性，進而提高了搜索效率和搜索質量；2）將改進logistic混沌映射引入到局部最優位置附近，有助于算法跳出局部最優，提高局部搜索能力。

2.2 高斯變異

為了解決算法在后期迭代過程中種群多樣性減少的問題，加入高斯變異操作[31]，如式(12)。

式中：為一個高斯分布的隨機變量，其均值為0，方差為1；P為當前種群在第維的位置信息；P為當前代中適應度值最差的個體在第維的位置信息；″為高斯變異后種群在第維的位置信息，其中，∈。

選取當前最差位置進行變異操作，不僅能降低計算維度和復雜度，還能增加種群多樣性，此外，這也增強了算法的全局搜索能力。

2.3 CGSOA算法

全局混沌高斯融合的海鷗優化算法具體實現偽代碼如下：

1）設置種群數量popsize、規模（維度）、最大迭代次數maxGen、初始值的上下界（和l）、=2、=1、=1等參數；

2）利用改進logistic混沌初始化海鷗種群，并映射到解空間的取值范圍內；

%以目標函數為適應度值，計算初始種群中每只海鷗的適應度值%；

3）for= 1:popsize

{計算每只海鷗的適應度值；}

輸出當前海鷗最優適應度值（_best）及對應的位置（best），和當前海鷗最差適應度值（_bad）及對應位置（bad）；

4）while(< maxGen)

{rand∈(0,1);∈[0,2π]；

利用式(1)—(7)計算海鷗位置；

計算海鷗位置的適應度值(i)；

在當前最優位置利用式(11)計算新位置（混沌）；

在當前最差位置利用式(12)計算新位置（高斯）；

計算引入混沌或者高斯的海鷗新位置的適應度值(_new)和對應位置_new；

%更新最優適應度值及位置%

if ((_new) <(best))

best=_new；

_best =(_new)；

end

=+1；

}

5）判斷是否達到最大迭代次數，若是，則輸出全局最優適應度值及對應位置；否則，返回到4）。

3 算法測試與仿真結果分析

為了驗證CGSOA算法的有效性和尋優能力，將該算法與天牛須算法[32]（Beetle Antennae Search，BAS）、PSO算法[33]、蟻群算法[34]（Ant Colony Optim-ization，ACO）和常規SOA算法進行實驗分析。利用6個不同類型的基準函數進行仿真測試，函數如表1所示。

其中，1、2為高維單峰基準函數，3、4為高維多峰基準函數，5、6為固定維多峰基準函數。利用不同類型的基準函數測試，可驗證本文算法的局部搜索能力、種群多樣性，尤其是多峰函數中，存在多個局部最優，可驗證本文算法跳出局部最優的能力和全局搜索的能力。為維度，0表示為（01, 02, 03,…, 0）。

表1 6個測試函數

Tab.1 6 test functions

3.1 參數設置

本文中所比較算法的參數設置如表2所示。其中，在BAS算法中，表示步長衰減因子，表示天牛須兩須之間的距離或感知長度，step表示搜索步長；PSO算法中，1和2為加速因子，為慣性權重；ACO算法中，表示信息素揮發系數，表示轉移概率；SOA算法中，為控制系數，和為螺旋形狀的相關系數。

表2 各算法主要參數設置

Tab.2 Main parameters setting of each algorithm

3.2 仿真結果及分析

對1—6（等同于下文1—6）進行函數測試時，各算法的迭代次數設置為1000次，種群數量為30個，各算法獨立運行30次的實驗結果如表3所示（mean為均值，SD為標準差）。函數在不同算法優化下的收斂曲線如圖3—8所示。

從表3中可以看出，在6個測試函數上，本文所提出的CGSOA算法的測試結果相對較優。1、2的理想值都為0，故均值mean越接近0越好，且SD越接近0，說明算法越穩定，尋優性能越好。由結果可知，CGSOA算法的尋優結果最接近0，SOA算法次之，BAS算法最差，表明CGSOA算法在高維單峰函數上具有很強的局部搜索能力。在3、4中，理想值均為0，對3函數尋優時，CGSOA算法與PSO算法和ACO算法的尋優結果相差不大，但也是最優，對4尋優時，CGSOA算法比其他算法表現出更好的性能，其中BAS算法的尋優效果最差。以上結果表明，CGSOA算法具有很好的全局搜索能力。在固定低維函數5、6中，理想值分別為?8.0393和?1.0316，從表3中可看出，PSO算法、ACO算法和CGSOA算法均能尋得最優值，但SD有差異，其中CGSOA算法相對于ACO算法和PSO算法略差，但優于BAS算法和常規SOA算法。在高維函數尋優中，CGSOA算法有明顯的優勢，在低維函數中，PSO算法和ACO算法較優。從圖3—8的函數收斂曲線中可以看出，SOA算法在迭代初期的表現最差。圖3的1函數中，CGSOA算法在迭代初期就逐漸收斂于最優值。圖4的2函數中，CGSOA算法在迭代10次之前只比常規SOA算法強，但第10次之后，比其他算法表現出更強的尋優能力。從圖5、圖6中可以看出，對3和4函數尋優時，在迭代后期，CGSOA算法都能比其他算法更早收斂于最優值。而從圖7、圖8中可以看出，CGSOA算法的收斂效果略差于PSO算法和ACO算法，但優于其他算法。

表3 各算法實驗結果對比

Tab.3 Comparison of experimental results of each algorithm

圖3 函數f1收斂曲線

函數測試結果表明，CGSOA算法在高維函數上的收斂速度、收斂精度和穩定性優于其他算法，低維函數上略遜于PSO算法和ACO算法，但也比常規SOA算法性能好。說明針對局部最優、收斂過早、高維等問題，本文算法具有較好的收斂性、尋優性、穩定性，且搜索能力和開發能力較強。

圖4 函數f2收斂曲線

圖5 函數f3收斂曲線

圖6 函數f4收斂曲線

圖7 函數f5收斂曲線

圖8 函數f6收斂曲線

4 AlCoCrNiFe涂層制備

4.1 實驗設計

在大氣等離子噴涂實驗中，噴涂距離過短，會導致粉末熔融效果不好，不利于粉末沉積在基體上，且距離較短時，粉末獲得動能較小，基體受到的沖擊力較小，使得基體過熱，發生過燒現象，導致粘結性降低。噴涂距離過大時，噴槍的焰流溫度降低，熔融粉末獲得的動能降低，導致粉末在沉積過程中粘結性降低，即結合強度降低。

噴涂電流主要影響焰流能量密度及氣焰流速。噴涂電流過小，焰流能量密度低，粉末熔融較差，降低涂層的力學性能。噴涂電流過大，會對基體產生過燒現象，使得結合處產生氣孔及氧化物等缺陷，降低涂層質量。當電流變化時，配合電壓的使用，能適當調節噴涂功率，以得到相應的焰流溫度，提高涂層質量。

送粉載氣過小時，每次到達槍口的熔融粉末較少，基體沉積較薄，且多次噴涂更容易影響已噴涂上的涂層，增加涂層內部氣孔及金屬氧化物夾雜，導致涂層性能降低。送粉載氣過大時，焰流量大，粉末熔融不好或只有部分粉末熔融較好，熔融不充分的粉末沉積在基體上，會降低涂層質量。送粉電壓對涂層的影響與送粉載氣一致，過低時，送粉量小，易產生氣孔及夾渣的缺陷；過高時，粉末熔融效果不理想，從而降低涂層力學性能。

在本次實驗中，采用由廣州三鑫金屬科技有限公司生產的SX-80等離子噴涂設備。選取噴涂距離、噴涂電流、噴涂電壓、送粉載氣、送粉電壓作為輸入，主次壓力恒定，機械手軌跡參數一定，即除噴涂距離、功率（電流、電壓）、送粉載氣、送粉電壓外，其他參數恒定。機械手的噴涂軌跡設置呈“Z”字形，每步的跨度為0.5 cm，為了保證噴涂的均勻性，每次編程控制機械手運行軌跡超出樣品邊緣一定距離，機械手運行軌跡如圖9所示。噴涂相關預備材料如表4所示。

圖9 機械手運行軌跡

表4 噴涂相關預備材料

Tab.4 Preparation materials for spraying

采用X射線衍射儀（XRD, Bruker, D8-Advance 2009, Germany）對AlCoCrNiFe高熵合金粉末及所制備的涂層進行物相分析，測試的2角范圍為10°～90°。為了分析粉末元素分布，使用配備EDS的掃描電子顯微鏡（SEM，FEI-Quanta 600）對粉末進行表征。拉伸強度在萬能拉伸機上（WDW-100）測試，以2 mm/min的拉伸速率進行實驗，直到涂層斷裂。顯微硬度在顯微維氏硬度計（HMV-2T）下測量，在室溫下對樣品的橫截面進行維氏硬度測試，試驗壓頭的載荷設置為200 g，保壓時間為10 s，然后讓維氏硬度壓頭沿著基體向AlCoCrNiFe涂層方向進行測試，每個位置保證至少5個壓痕，最終求平均值。試驗所購的高熵合金粉各元素是等比分布的，EDS元素分布圖如圖10所示，可看出，粉末大多呈球形分布，各元素近似均勻分布于粉末顆粒中。高熵合金的粉末粒徑通過相關電鏡圖像的定量分析圖像（Image J）測量得到，如圖11所示，可以看出粉末粒徑主要集中在15～45 μm。

在BP神經網絡上，輸入層節點數為5，輸出層節點數為2，隱藏層節點數為10。其中訓練集為20組，測試集為5組（樣本5、10、15、20、25）。工藝參數優化模型及噴涂流程如圖12所示，通過正交試驗法[35]獲取樣本數據參數及實驗結果如表5所示。

圖10 AlCoCrNiFe高熵合金粉末的SEM形貌圖和元素分布圖

圖11 AlCoCrNiFe高熵合金粉末粒徑分布

4.2 適應度評價函數

在本試驗中，以結合強度和顯微硬度作為涂層性能的評價指標，為了兼顧這兩個指標，本文采用式(13)作為適應度評價函數。

式中：a和b為權重因子。當a=1、b=0時，為單一結合強度優化；當a=0、b=1時，為單一顯微硬度優化。以上兩種情況為單目標優化。在本文中，為了平衡兩個涂層性能指標的權重，即多目標優化，取a=b=1。q(xi)和y(xi)分別為模型輸出的結合強度和顯微硬度，qmax和ymax分別為最大拉伸結合強度和最大顯微硬度。為了使兩個性能指標均能達到較優狀態，則保證，，在此約束條件下，結合強度和顯微硬度可達到較優性能。

表5 樣本數據參數及實驗結果

Tab.5 Sample data parameters and experimental results

續表5

4.3 實驗結果及分析

利用CGSOA算法優化BP神經網絡的訓練模型預測值與實際噴涂值的結果如圖13所示，測試模型預測值與實際噴涂值結果如圖14所示。從圖13可以看出，訓練模型的預測值與實際噴涂值非常接近；從圖14看出，將5組數據輸入到模型中，測試表明，預測值與實際值很接近，說明該模型的預測性能較好。

將影響變量在變化范圍內的參數隨機組合，作為該模型的輸入，通過50次迭代計算，CGSOA算法優化BP神經網絡模型的適應度值曲線如圖15所示。

當適應度值達到最大值1.0316時，反向迭代得出的最佳工藝參數為：噴涂距離99.7 mm，噴涂電流649.6 A，噴涂電壓56.3 V，送粉載氣203.1 L/h，送粉電壓5.1 V。預測結合強度和顯微硬度分別為24.44 MPa、598.85 HV。根據優化后的工藝參數制備AlCoCrNiFe高熵合金涂層，對噴涂AlCoCrNiFe粉末和制備的涂層進行XRD分析，如圖16所示。由XRD圖可以看出，涂層和高熵粉末都由無序BCC（A2）和有序BCC（B2）組成，相結構未發生改變，但所制備涂層的衍射峰強明顯增加。對制備的涂層樣品進行拉伸及顯微硬度測試，結合強度和顯微硬度的平均值分別為25.2 MPa、616.8HV，與預測出的結合強度與顯微硬度的相對誤差分別為3.02%、2.91%。綜上，在該工藝參數下制備的AlCoCrNiFe涂層性能較好。

圖13 訓練模型預測值與實際噴涂值

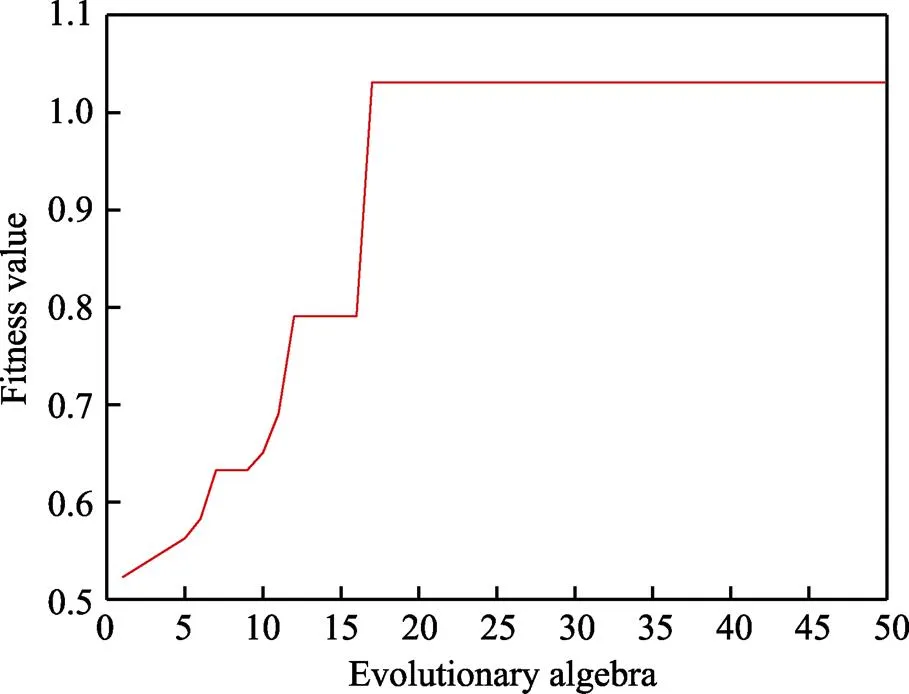
圖15 CGSOA算法優化得到的適應度值曲線

圖16 涂層和噴涂高熵粉末的XRD分析

5 結論

1）全局混沌高斯混合的海鷗優化算法解決了基本海鷗優化算法“早熟”、種群多樣性減少等問題，具有收斂性能好、尋優精度高、局部和全局搜索能力強等優點。

2）利用全局混沌高斯融合的海鷗優化算法優化BP神經網絡獲得的噴涂工藝參數為：噴涂距離 99.7 mm，噴涂電流649.6 A，噴涂電壓56.3 V，送粉載氣203.1 L/h，送粉電壓5.1 V。預測結合強度和顯微硬度分別為24.44 MPa、598.85HV。在該工藝參數下制備AlCoCrNiFe高熵合金涂層，得到結合強度和顯微硬度分別為25.2 MPa、616.8HV，相對誤差分別為3.02%、2.91%，在一定誤差范圍內，該涂層性能較好。CGSOA-BPNN為等離子噴涂工藝參數的選取提供了科學的指導性。

3）在材料性能預測、工藝參數尋優等方面，利用群智能優化算法與神經網絡結合的模型，預測精度更高，可靠性更強，解決了多工藝參數尋優中單一BP神經網絡過擬合導致預測誤差大的問題。

4）影響涂層性能的因素較多，在后期的研究中，將先對影響因素進行分析或降維處理，再利用智能算法或模型或機器學習等工具對其進行深入的研究。

[1] LI Qiao-lei, SONG Peng, LV K, et al. Fracture Behaviour of Ceramic-Metallic Glass Gradient Transition Coating[J]. Ceramics International, 2019, 45(5): 5566-5576.

[2] WANG Liang-quan, ZHANG Fan-yong, YAN Shu, et al. Microstructure Evolution and Mechanical Properties of Atmosphere Plasma Sprayed AlCoCrFeNi High-entropy Alloy Coatings under Post-annealing[J]. Journal of Alloys and Compounds, 2021, 872: 159607.

[3] CALVO-DAHLBORG M, MEHRABAN S, LAVERY N P, et al. Prediction of Phase, Hardness and Density of High Entropy Alloys Based on Their Electronic Structure and Average Radius[J]. Journal of Alloys and Compounds, 2021, 865: 158799.

[4] MEGHWAL A, ANUPAM A, LUZIN V, et al. Multiscale Mechanical Performance and Corrosion Behaviour of Plasma Sprayed AlCoCrFeNi High-entropy Alloy Coat-ings[J]. Journal of Alloys and Compounds, 2021, 854: 157140.

[5] 康靚, 米曉希, 王海蓮, 等. 人工神經網絡在材料科學中的研究進展[J]. 材料導報, 2020, 34(21): 21172- 21179.

KANG Jing, MI Xiao-xi, WANG Hai-lian, et al. Research Progress of Artificial Neural Networks in Material Science[J]. Materials Review, 2020, 34(21): 21172-21179.

[6] 吳艷鵬, 魏劍輝, 李文戈, 等. 鋁合金表面等離子噴涂Al2O3-3%TiO2復合涂層工藝參數優化的研究[J]. 表面技術, 2019, 48(6): 322-331.

WU Yan-peng, WEI Jian-hui, LI Wen-ge, et al. Optimization of Plasma Spraying Process Parameters for Al2O3-3%TiO2Composite Coating on Aluminum Alloy[J]. Surface Technology, 2019, 48(6): 322-331.

[7] 路廣明, 烏日開西·艾依提. 等離子噴涂TiO2基涂層工藝參數優化研究[J]. 表面技術, 2018, 47(4): 73-80.

LU Guang-ming, WURIKAIXI·Aiyiti. Process Parameter Optimization of Plasma Sprayed TiO2-based Coatings[J]. Surface Technology, 2018, 47(4): 73-80.

[8] 夏衛生, 張海鷗, 王桂蘭, 等. 神經網絡在預測等離子噴涂Ni合金涂層質量中的應用[J]. 機械科學與技術, 2010, 29(8): 1008-1011.

XIA Wei-sheng, ZHANG Hai-ou, WANG Gui-lan, et al. Application of Artificial Neural Network to Quality Prediction of Ni Alloy Coatings Fabricated by Plasma Spraying[J]. Mechanical Science and Technology for Aerospace Engineering, 2010, 29(8): 1008-1011.

[9] MOJENA M A R, ROCA A S, ZAMORA R S, et al. Neural Network Analysis for Erosive Wear of Hard Coatings Deposited by Thermal Spray: Influence of Microstructure and Mechanical Properties[J]. Wear, 2017, 376-377: 557-565.

[10] BECKER A, FALS H D C, ROCA A S, et al. Artificial Neural Networks Applied to the Analysis of Performance and Wear Resistance of Binary Coatings Cr3C2-37WC-18M and WC-20Cr3C2-7Ni[J]. Wear, 2021, 477: 203797.

[11] PATURI U M R, CHERUKU S, GEEREDDY S R. Process Modeling and Parameter Optimization of Surface Coatings Using Artificial Neural Networks (ANNs): State-of-the-Art Review[J]. Materials Today: Proceedings, 2021, 38: 2764-2774.

[12] HUEN W Y, LEE H, VIMONSATIT V, et al. Nano-mechanical Properties of Thermal Arc Sprayed Coating Using Continuous Stiffness Measurement and Artificial Neural Network[J]. Surface and Coatings Technology, 2019, 366: 266-276.

[13] LIU Mei-mei, YU Ze-xin, ZHANG Yi-cha, et al. Prediction and Analysis of High Velocity Oxy Fuel (HVOF) Sprayed Coating Using Artificial Neural Network[J]. Surface and Coatings Technology, 2019, 378: 124988.

[14] ZHU Jin-wei, WANG Xin-zhi, KOU Lu-yao, et al. Pred-iction of Control Parameters Corresponding to In-Flight Particles in Atmospheric Plasma Spray Employing Conv-olutional Neural Networks[J]. Surface and Coatings Tech-nology, 2020, 394: 125862.

[15] 汪劉應, 王漢功, 華紹春, 等. 用GA-BP算法研究超音速電弧噴涂JCW-S-AM涂層顯微硬度與工藝參數間的關系[J]. 稀有金屬材料與工程, 2006, 35(4): 634-637.

WANG Liu-ying, WANG Han-gong, HUA Shao-chun, et al. Study on Relation between the Microhardness of JCW-S-AM Coatings Prepared by High Velocity Arc Spray and the Process Parameters Using GA-BP Arithm-etic[J]. Rare Metal Materials and Engineering, 2006, 35(4): 634-637.

[16] 華紹春, 王漢功, 汪劉應, 等. 微弧等離子噴涂AT13納米涂層的工藝優化[J]. 無機材料學報, 2007, 22(3): 560-564.

HUA Shao-chun, WANG Han-gong, WANG Liu-ying, et al. Optimization of the Process Parameters of Nano-structured AT13 Coatings Prepared by Micro-Plasma Spraying[J]. Journal of Inorganic Materials, 2007, 22(3): 560-564.

[17] 王東生, 楊斌, 田宗軍, 等. 基于遺傳神經網絡的等離子噴涂納米ZrO2-7%Y2O3涂層工藝參數優化[J]. 焊接學報, 2013, 34(3): 10-14.

WANG Dong-sheng, YANG Bin, TIAN Zong-jun, et al. Process Parameters Optimization of Nanostructured ZrO2-7%Y2O3Coating Deposited by Plasma Spraying Based on Genetic Algorithms and Neural Networks[J]. Transactions of the China Welding Institution, 2013, 34(3): 10-14.

[18] 楊振凱, 王海軍, 劉明, 等. 基于BP神經網絡的Fe基合金粉末噴涂工藝參數優化[J]. 表面技術, 2015, 44(9): 1-6.

YANG Zhen-kai, WANG Hai-jun, LIU Ming, et al. Optimization of Spraying Process Parameters for Fe-based Alloy Based on BP Neural Network Model[J]. Surface Technology, 2015, 44(9): 1-6.

[19] 帥茂杭, 熊國江, 胡曉, 等. 基于改進多目標骨干粒子群算法的電力系統環境經濟調度[J/OL]. 控制與決策, 2021: [2021-03-04]. https://kns.cnki.net/kcms/detail/detail. aspx?dbcode=CAPJ&dbname=CAPJLAST&filename=KZYC2021030300F&uniplatform=NZKPT&v=OKAgri6ShmPluCvjAxDaV_oERjlgUjlQSSLkVqEDCDeN7wEvf3rSqkYxAev7cHUC

SHUAI Mao-hang, XIONG Guo-jiang, HU Xiao, et al. Economic Emission Dispatch of Power System Based on Improved Bare-Bone Multi-Objective Particle Swarm Optimization Algorithm[J/OL]. Control and Decision, 2021: [2021-03-04]. https://kns.cnki.net/kcms/detail/detail. aspx?dbcode=CAPJ&dbname=CAPJLAST&filename=KZYC2021030300F&uniplatform=NZKPT&v=OKAgri6ShmPluCvjAxDaV_oERjlgUjlQSSLkVqEDCDeN7wEvf3rSqkYxAev7cHUC

[20] 張強, 李盼池, 王梅. 基于自適應進化策略的人工蜂群優化算法[J]. 電子科技大學學報, 2019, 48(4): 560-566.

ZHANG Qiang, LI Pan-chi, WANG Mei. Artificial Bee Colony Optimization Algorithm Based on Adaptive Evolution Strategy[J]. Journal of University of Electronic Science and Technology of China, 2019, 48(4): 560-566.

[21] 馬小陸, 梅宏. 基于改進勢場蟻群算法的移動機器人全局路徑規劃[J]. 機械工程學報, 2021, 57(1): 19-27.

MA Xiao-lu, MEI Hong. Mobile Robot Global Path Planning Based on Improved Ant Colony System Algori-thm with Potential Field[J]. Journal of Mechanical Engin-eering, 2021, 57(1): 19-27.

[22] 柳長源, 任宇艷, 畢曉君. 基于改進螢火蟲算法的區域交通信號配時優化[J]. 控制與決策, 2020, 35(12): 2829-2834.

LIU Chang-yuan, REN Yu-yan, BI Xiao-jun. Timing Opti-mization of Regional Traffic Signals Based on Impro-ved Firefly Algorithm[J]. Control and Decision, 2020, 35(12): 2829-2834.

[23] 崔雪婷, 李穎, 范嘉豪. 全局混沌蝙蝠優化算法[J]. 東北大學學報(自然科學版), 2020, 41(4): 488-491.

CUI Xue-ting, LI Ying, FAN Jia-hao. Global Chaotic Bat Optimization Algorithm[J]. Journal of Northeastern Univ-ersity (Natural Science), 2020, 41(4): 488-491.

[24] 湯安迪, 韓統, 徐登武, 等. 混沌多精英鯨魚優化算法[J]. 北京航空航天大學學報, 2021, 47(7): 1481-1494.

TANG An-di, HAN Tong, XU Deng-wu, et al. Chaotic Multi-Leader Whale Optimization Algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(7): 1481-1494.

[25] ZHANG Cheng-long, DING Shi-fei. A Stochastic Configuration Network Based on Chaotic Sparrow Search Algorithm[J]. Knowledge-Based Systems, 2021, 220: 106924.

[26] DHIMAN G, KUMAR V. Seagull Optimization Algo-rithm: Theory and Its Applications for Large-Scale Indust-rial Engineering Problems[J]. Knowledge-Based Systems, 2019, 165: 169-196.

[27] CAO Yan, LI Yi-qing, ZHANG Geng, et al. Experimental Modeling of PEM Fuel Cells Using A New Improved Seagull Optimization Algorithm[J]. Energy Reports, 2019, 5: 1616-1625.

[28] LEI Gang, SONG He-qing, RODRIGUEZ D. Power Generation Cost Minimization of the Grid-Connected Hybrid Renewable Energy System Through Optimal Sizing Using the Modified Seagull Optimization Techn-ique[J]. Energy Reports, 2020, 6: 3365-3376.

[29] 陳志剛, 梁滌青, 鄧小鴻, 等. Logistic混沌映射性能分析與改進[J]. 電子與信息學報, 2016, 38(6): 1547-1551.

CHEN Zhi-gang, LIANG Di-qing, DENG Xiao-hong, et al. Performance Analysis and Improvement of Logistic Chaotic Mapping[J]. Journal of Electronics & Information Technology, 2016, 38(6): 1547-1551.

[30] XU Yue-ting, CHEN Hui-ling, HEIDARI A A, et al. An Efficient Chaotic Mutative Moth-Flame-Inspired Optim-izer for Global Optimization Tasks[J]. Expert Systems with Applications, 2019, 129: 135-155.

[31] 盧青波, 張學良, 溫淑花, 等. 高斯變異差分進化算法及其應用研究[J]. 工程設計學報, 2012, 19(5): 372-378.

LU Qing-bo, ZHANG Xue-liang, WEN Shu-hua, et al. Research on Differential Evolution Algorithm Based on Gauss Mutation and Its Application[J]. Journal of Engine-ering Design, 2012, 19(5): 372-378.

[32] JIANG X, LI S. BAS: Beetle Antennae Search Algorithm for Optimization Problems[J]. International Journal of Robotics and Control. 2018, 1(1): 1-5.

[33] KENNEDY J, EBERHART R. Particle Swarm Optimiz-ation[C]//In Proceedings of the 1995 IEEE International Conference.USA: IEEE, 1995: 1942-1948.

[34] PAN M Z, LI C, GAO R, et al. Photovoltaic Power Forecasting Based on A Support Vector Machine with Improved Ant Colony Optimization[J]. Journal of Cleaner Production, 2020, 277: 123948.

[35] 劉貴民, 楊忠須, 張一帆, 等. 基于正交試驗法的超音速等離子噴涂鉬涂層組織及性能研究[J]. 兵工學報, 2016, 37(8): 1489-1496.

LIU Gui-min, YANG Zhong-xu, ZHANG Yi-fan, et al. Research on Microstructure and Properties of Supersonic Plasma Sprayed Mo Coating Based on Orthogonal Expe-ri-ment[J]. Acta Armamentarii, 2016, 37(8): 1489-1496.

Optimization of Plasma Spraying Process Parameters of AlCoCrNiFe High Entropy Alloy Coating Based on CGSOA-BPNN

LI Zan, ZHANG Chang-sheng, MA Tao,WANG Zhuo

(a. Faculty of Information Engineering and Automation, b. Faculty of Materials Science and Engineering, Kunming University of Science and Technology, Kunming 650093, China)

The aims is to solve the problem of difficult parameter selection caused by the coupling of plasma spraying process parameters to improve the mechanical properties of the AlCoCrNiFe high entropy alloy coating. An algorithm which seagull optimization algorithm based on global chaotic and Gaussian fusion (CGSOA) is proposed to optimize the weights and thresholds so that BP (Back Propagation) neural network training outputs ideal control parameters. The improved logistic chaotic sequence is used to realize the global search of the initial population of network parameters, and the initial quality of weights and thresholds is improved; the improved logistic mapping is introduced to jump out of the local optimum, and the local search capability is strengthened to improve the accuracy of the algorithm convergence; the introduction of Gaussian mutation increases the diversity of the population, improve the global search capability; select 6 benchmark functions to test the BAS, PSO, ACO, SOA and CGSOA algorithms. The simulation results show that the proposed algorithm had faster convergence speed, higher optimization accuracy and stability. CGSOA algorithm optimizes the BP neural network to obtain the best control amount: spraying distance 99.7 mm, spraying current 649.6 A, spraying voltage 56.3 V, powder feeding carrier gas 203.1 L/h, powder feeding voltage 5.1 V. The spraying test with this parameter shows that the bonding strength and microhardness of the coating were 25.2 MPa and 616.8HV, respectively, and the relative errors with the predicted value of the model were 3.02% and 2.91%, respectively. This result verifies the feasibility of applying the CGSOA algorithm to actual projects. CGSOA-BPNN has a certain guiding significance for optimizing the plasma spraying process parameters of AlCoCrNiFe high-entropy alloy coating, thereby improving the coating performance.

plasma spraying; high entropy alloy coating; process parameter optimization; BP neural network; seagull optimization algorithm; improved logistic chaos; gaussian mutation

2021-04-22；

2021-10-12

LI Zan (1996—), Male, Master, Research focus: intelligent optimization algorithm, industrial modeling and parameter optimization.

張長勝（1970—），男，博士，副教授，主要研究方向為智能優化算法、復雜工業建模及圖像處理。

Corresponding author：ZHANG Chang-sheng (1970—), Male, Doctor, Associate professor, Research focus: intelligent optimization algorithms, complex industrial modeling and image processing.

李贊, 張長勝, 馬濤,等.基于CGSOA-BPNN優化AlCoCrNiFe高熵合金涂層等離子噴涂工藝參數[J]. 表面技術, 2022, 51(1): 311-324.

TG174.442；TP391.9

A

1001-3660(2022)01-0311-14

10.16490/j.cnki.issn.1001-3660.2022.01.034

2021-04-22；

2021-10-12

國家自然科學基金（61963022，51665025）

Fund：Supported by National Natural Science Foundation of China (61963022, 51665025)

李贊（1996—），男，碩士研究生，主要研究方向為智能優化算法、工業建模及參數優化。

LI Zan, ZHANG Chang-sheng, MA Tao, et al. Optimization of Plasma Spraying Process Parameters of AlCoCrNiFe High Entropy Alloy Coating Based on CGSOA-BPNN[J]. Surface technology, 2022, 51(1): 311-324.