基于結構特征的織物熱傳遞性能預測研究進展

李金嶼 楊允出 劉鳴茗

摘 要：為了預測織物熱傳遞性能，更好地進行織物設計，從而提高織物的熱舒適性能，從不同建模方法的角度介紹了與織物結構參數及內部特征相關的織物熱傳遞性能預測模型，包括統計模型、人工神經網絡模型、數學理論模型和有限元模型，并分析了各類預測模型的特點和適用范圍。回顧并總結了近年來國內外織物傳熱模擬的研究現狀。此外，總結了含水分織物以及含相變材料織物的熱傳遞模型及研究進展。綜合以上文獻分析，指出可通過優化織物結構特征提升織物熱傳遞性能，并提出織物傳熱性能預測研究的發展趨勢，為服裝熱舒適性研究提供新的思路。

關鍵詞：織物結構;熱傳遞性能;預測模型;傳熱模擬;建模方法

中圖分類號：TS101.8

文獻標志碼：A

文章編號：1009-265X（2022）01-0018-08

Abstract： In order to predict the heat transfer properties of fabrics accurately， design fabrics better， and improve the thermal comfort of fabrics， the prediction models of heat transfer properties related to the structural parameters and internal characteristics of fabrics are introduced from different modeling methods， including statistical model， artificial neural network model， mathematical theoretical model and finite element model， the characteristics and application scope of different kinds of prediction models are analyzed. The research status of heat transfer simulation of fabrics at home and abroad in recent years is reviewed. Besides， the heat transfer model and research progress of fabrics containing moisture and fabrics containing phase change materials are summarized. Based on the above literature analysis， it is pointed out that the heat transfer properties of fabrics can be enhanced by optimizing the structural characteristics of fabrics， and the development trend of studies on the prediction of heat transfer properties of fabrics is proposed， so as to provide a new idea for the research of thermal comfort of garments.

Key words： fabric structure; heat transfer properties; prediction model; heat transfer simulation; modeling method

織物結構特征是其服用性能的決定性因素之一，織物中熱量傳遞和溫度分布情況會受織物結構特征的影響，研究織物和紗線的結構特征及基本參數對織物傳熱性能的影響十分重要[1-3]。與傳統的實驗測試方法相比，利用織物熱傳遞性能預測模型能方便快捷地獲取織物熱導率、熱阻、克羅值等表征織物傳熱性能的指標，可以更好地進行織物和服裝設計，從而獲得相應的服用性能，避免樣衣制作環節，節約時間及成本[4-5]。建立織物熱傳遞性能預測模型的方法有很多，常見的有統計方法、神經網絡算法、分形建模、物理建模、數學建模、有限元建模等[6]。

近年來，織物熱傳遞性能的預測研究取得了一定進展。一些學者運用數值方法預測研究了織物交織規律對織物傳熱性能的影響[4-5]，還有學者綜述了多孔織物熱質傳遞的數值模擬研究進展[7-8]。但此前的研究多基于純數值理論的模擬預測，針對不同建模方法的織物熱傳遞性能預測的綜述性研究較少。本文概述了織物結構特征對其傳熱性能的影響預測研究，介紹了國內外不同類型的織物熱傳遞性能預測模型，包括統計模型、人工神經網絡模型、數學理論模型和有限元模型，對比分析了不同類型預測模型的特點及適用范圍。此外，還總結了含有不同組分的織物傳熱模擬的相關研究，旨在更好地了解織物熱傳遞性能預測的研究現狀和發展前景，為織物服用性能的優化以及新型織物的開發提供參考。

1 織物熱傳遞性能預測模型

1.1 統計建模和人工神經網絡

研究織物各結構參數對傳熱性能的綜合影響時，可以借助于統計模型來預測熱阻。Bhattacharjee等[9]基于響應面統計分析法，建立了兩種熱流條件下的多項式方程。結果表明，當以經緯紗密度、紗線間距、厚度、織物重量、孔隙率等結構參數均作為變量時，可得到響應函數，且所得熱阻預測值的測定系數高，平均誤差小。Afzal等[10]采用不同線密度和滌棉混紡比的紗線在不同的緊密度下編織而成織物樣品，對針織物的各項參數進行測試和計算，利用這些輸入參數建立作為預測滌棉混紡針織物熱阻的二次型模型，如式（1）-式（3）所示：

Rfab=-234.11 + 3.11Tt + 117.97C + 7.73l-0.04T2t-17.57C2-0.37Tt×C（1）

Rfab=-271.42+110.64C+211.33h-0.05m-13.85C2+0.0002m2-37.65C×h+0.05C×m-0.24h×m（2）

Rfab=-157.44 + 2.61Tt + 40.82C-38.31l + 274.92h-0.23m-0.05T2t + 16.23C×l-98.88C×h + 0.08C×m（3）

式中：Tt為紗線線密度，tex;C為紗線比熱，J/（g·K）;l為線圈長度，mm;h為織物厚度，mm;m為織物面密度，g/m2。

近年來，人工神經網絡（ANN）被廣泛應用于包括紡織材料在內的各種材料的性能預測研究中[11-12]。ANN的目標是利用實驗數據建立一個能夠精確反映輸入和輸出之間所具有的函數關系的模型。一個典型的ANN具有前饋結構，由三層或多層神經元組成，如圖1所示[13]。利用ANN系統預測織物傳熱性能時，將容易獲取的織物各結構參數作為系統的輸入層，如織物厚度、織物面密度、紗線組成成分、織物組織結構等;輸出層為織物傳熱性能的表征參數，如織物熱導率，其與織物組織結構、密度、紗線種類、含水率和溫度等因素相關。

ANN是預測織物傳熱性能的有效工具之一。Guenesoglu等[14]利用儀器測量了大量不同結構參數的針織物的穩態熱導率和瞬態熱接觸性能，將測試數據應用于ANN建模，然后用強回歸系數進行預測。ANN系統的輸入數據選擇為織物重量、織物厚度、織物密度、纖維密度、纖維熱導率等，輸出是熱導率和熱吸收率。Majumdar[13]和Alibi等[15]分別采用ANN對混紡針織物的熱導率進行了建模。將針織物結構類型（平針、羅紋和雙羅紋）、纖維比例、紗線的線密度、織物厚度和織物面密度等作為ANN模型的輸入參數，并分別研究了各輸入參數對織物熱導率的影響。Alibi等[15]提出了一種計算方法來選擇最優的神經網絡結構，以解決人工神經網絡的過擬合現象。與統計模型相比，人工神經網絡模型直接輸出熱導率等表征服裝舒適性的指標，具有優秀的數據處理能力，但不能從函數表達式上看出各結構參數與服裝舒適性指標的關系。為了保證模型精度，二者在建模時均需要大量的實驗數據。

1.2 數學理論模型

在一維穩態熱傳遞過程中，織物熱導率（λ）的定義及計算公式由傅里葉定律給出：

λ=Q·hA·ΔT·t（4）

式中：Q是傳導熱量，J;A是傳熱面積，m2;t是熱傳導時間，s;ΔT是下降溫度，K;h是織物厚度，m。織物熱阻（Rfab）與織物熱導率的關系如式（5）所示：

Rfab=hλ（5）

織物的熱阻可以用集總模型來計算，其中織物內部紗線、層間化合物和氣孔可以看作一個電阻系統，因此可以利用電阻串-并聯原理來計算織物熱阻值，如圖2所示[16]：

纖維排列分為平行和垂直于織物表面兩種方式，不同織物在纖維排列方面有明顯不同。Bogaty等[17]提出串-并聯理論模型來表達織物熱導率與織物內部結構的關系，將空氣和紗線集合體的有效熱導率定義為：

λe=x（vfibλfib+vairλair）+yλfibλairvairλfib+vfibλair（6）

式中：x和y分別是平行和垂直于傳熱方向纖維的有效體積分數，且x+y=1;λfib和λair分別是纖維和空氣的熱導率;vfib和vair分別為紗線和空氣的體積分數，且vf+va=1。類似地，Maxwell-Eucken模型[18-19]也描述了具有簡單物理結構織物的有效熱導率：

λe=λairvair+λfibvfib3λair2λair+λfibvair+vfib3λair2λair+λfib（7）

Levy[16]在式（7）基礎上提出了修正后的Maxwell-Eucken方程組：

λe=λair2λair+λfib-2（λair-λfib）F2λair+λfib+（λair-λfib）F

F=2/G-1+vfib-（2/G-1+vfib）2-8vfib/G2

G=（λair-λfib）2（λair+λfib）2+λairλfib/2（8）

Halaoua等[20]在式（6）的基礎上，選取平紋織物為研究對象，通過將其劃分為相似單元和相等單元，提出一個可預測纖維材料在織物形態、紗線形態、甚至纖維形態的有效熱導率的數學模型。蔡彥等[6]通過分析織物內部組織結構，將組織循環內紗線分布分為交織點紗線重疊區域、經（緯）紗交替穿越區域、經（緯）紗懸浮區域、孔隙區域六類，并通過截面積相等的方式將不規則紗線等效轉化為規則的幾何體。通過分析組織循環內各區域紗線與空氣分布情況，結合式（6）等效熱導率串-并聯模型，建立了各微元的等效熱導率數值模型。Seo等[21]采用熱電模擬方法研究了紡紗型碳/酚醛（C/P）復合材料的熱導率。該方法基于描述熱勢分布和電勢分布的偏微分方程之間的相似性，將復合材料分成若干個傳導單元，通過建立一個串-并聯等效熱阻網絡，預測復合材料的熱導率。Wang等[22]提出了一種具有多個連續相的非均勻材料的結構模型。用3種方法導出了相應的計算有效熱導率的方程組：

λe=λs/2（1+8λp/λs-1）

λp=∑Ni=1λivi，λs=1/∑Ni=1viλi（9）

式中：λi是織物第i種組分的熱導率;vi是織物第i種組分的體積分數。

還有一些學者給出根據織物結構特征預測熱阻的數學理論模型。Kothari等[23]基于多孔材料傳熱第一原理，建立了用于預測織物熱傳導和輻射傳熱的數學模型，并對該模型進行了驗證，給出了一個利用織物結構參數預測機織物穩態傳熱性能的數學模型。織物傳導產生的總熱阻：

Rcon=ΔT·R2p1p2Qcon（10）

輻射換熱的熱阻（空氣部分）：

Rrad.air=ΔT·R2p1p2Qrad（11）

輻射換熱的熱阻（紗線部分）：

Rrad.yarn=ΔTqT（12）

式中：R是一個單元織物中紗線的數量;p1和p2分別是經紗和緯紗間的距離，m;Qcon和Qrad分別是單位時間內傳導熱流量和輻射熱流量，W;qT是薄層絕熱纖維單位面積單位時間內輻射熱流總量，W/m2。織物的總熱損失可以看作是皮膚和大氣之間一個類似并聯電阻的系統，因此，織物總熱阻方程表示為：

Rtotal=[R-1con+R-1rad.air+R-1rad.yarn]-1（13）

Wei等[24]提出了一種根據織物微觀結構參數計算機織物和針織物熱阻的修正模型。通過對織物簡化基本單元傳熱過程的分析，建立了計算織物熱阻的數學模型。首先提出機織物和針織物的熱阻計算方程如下：

Rfab=hλairλfib-a（λfib-λair）λfib-（λfib-λair）（a-ρfabρfib）（14）

式中：a是織物的結構參數;ρfab和ρfib分別是織物和纖維的體積密度，kg/m3。利用織物樣品的實驗值進行修正檢驗之后提出的數學模型為：

Rfab=h1.043e-0.16hλairλfib-a（λfib-λair）λfib-（λfib-λair）（a-ρfabρfib）（15）

計算了織物熱阻與織物結構參數之間的Pearson相關系數，由高到低依次為：織物厚度、織物體積密度、織物結構參數、纖維體積密度和纖維熱導率。

數學理論模型多基于串-并聯原理，考慮織物內部物理結構對其傳熱性能的影響。表1是對上述數學理論模型的分類總結及特性對比。在織物熱傳遞性能預測的實際應用中，可以根據不同的織物特點和實際需求，進行合理選擇。

1.3 有限元建模

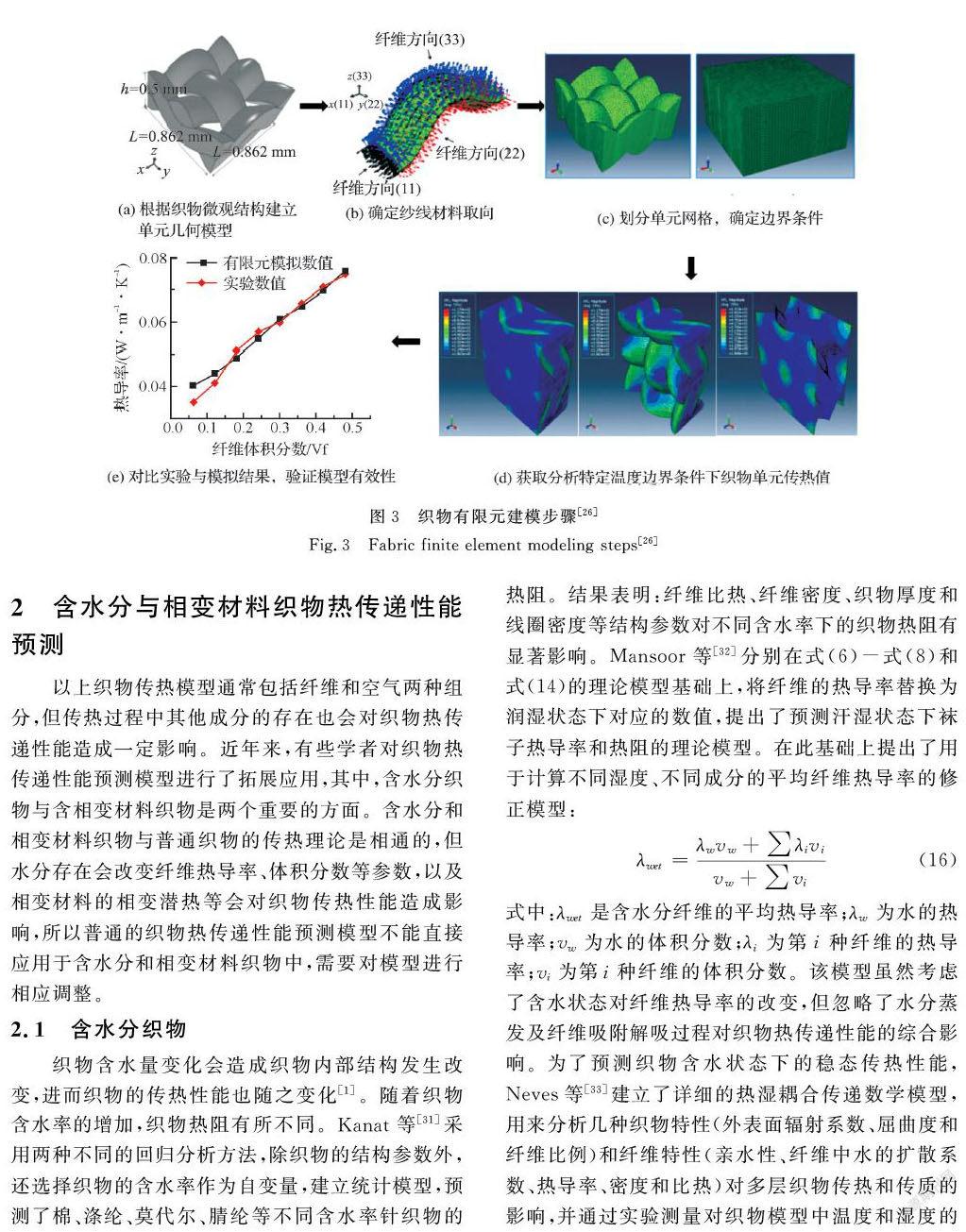
一些學者基于多孔材料傳熱理論建立織物有限元模型分析其熱傳遞性能。Siddiqui等[25]根據織物內部結構建立織物有限元模型，預測其有效熱導率和熱阻。實驗過程如圖3所示，首先利用掃描電子顯微鏡（SEM）對織物的內部參數進行分析，建立織物重復單元，進行網格劃分，并在不同的邊界條件下對織物單元進行傳熱分析。作者將預測得到的織物有效熱導率和熱阻值與實驗值進行了比較，并進一步探究了纖維熱導率隨溫度變化的規律以及纖維體積分數對織物有效熱導率的影響。Sun等[26]基于傳導、對流和輻射傳熱的理論模型，詳細介紹了織物和空氣層組成的織物系統的傳熱過程，建立了一種利用有限元軟件進行服裝舒適性研究的新方法，分析討論了織物與皮膚間空隙大小對熱傳遞性能的影響和不同環境溫度下織物層數對傳熱性能的影響。織物系統的結構參數包括織物層數、織物層間空氣的存在以及織物層間間隙的大小。Zheng等[27]考慮織物厚度、紗線路徑和紗線截面形狀等結構參數，利用TexGen自動建模方法建立了不同組織結構玻璃纖維織物的基本單元幾何模型，采用有限元方法模擬了織物傳熱過程。張潔等[28]運用有限元方法對三原組織織物的傳熱性能進行數值模擬，得出結論：在一定范圍內，織物緊度與織物的導熱性能呈正相關;在織物緊度相同時，熱傳遞性能優劣排序為：平紋織物、斜紋織物、緞紋織物。蔡彥等[29]為了探究織物接觸冷暖感，針對織物與皮膚接觸瞬間熱量傳導情況及其影響因素，用SEM對織物進行測量，得到織物內部紗線的幾何參數，將建立的織物三維幾何模型和毛羽層等效熱導率模型導入有限元分析軟件，結合等效熱導率的串-并聯模型進行仿真模擬。Wu等[30]通過有限元建模的方法研究了平紋混紡織物的熱傳遞性能。

織物有限元傳熱模擬不需要創建實物模型，具有可視化、易操作的優點，可進行織物微觀條件下的多種熱力學分析[27-28]。各種有限元分析軟件被廣泛應用于織物熱傳遞性能預測研究中，以ANSYS為例，其具有建模簡單、求解方便的特點[8]，設置不同織物結構參數和邊界條件可直接生成溫度和熱通量云圖，便于實驗結果的對比分析。利用有限元模型不能直接導出熱導率和熱阻等織物傳熱性能指標，而是通過模擬獲取織物傳熱過程中的溫度場分布情況，進一步分析表征織物的熱傳遞性能。

2 含水分與相變材料織物熱傳遞性能預測

以上織物傳熱模型通常包括纖維和空氣兩種組分，但傳熱過程中其他成分的存在也會對織物熱傳遞性能造成一定影響。近年來，有些學者對織物熱傳遞性能預測模型進行了拓展應用，其中，含水分織物與含相變材料織物是兩個重要的方面。含水分和相變材料織物與普通織物的傳熱理論是相通的，但水分存在會改變纖維熱導率、體積分數等參數，以及相變材料的相變潛熱等會對織物傳熱性能造成影響，所以普通的織物熱傳遞性能預測模型不能直接應用于含水分和相變材料織物中，需要對模型進行相應調整。

2.1 含水分織物

織物含水量變化會造成織物內部結構發生改變，進而織物的傳熱性能也隨之變化[1]。隨著織物含水率的增加，織物熱阻有所不同。Kanat等[31]采用兩種不同的回歸分析方法，除織物的結構參數外，還選擇織物的含水率作為自變量，建立統計模型，預測了棉、滌綸、莫代爾、腈綸等不同含水率針織物的熱阻。結果表明：纖維比熱、纖維密度、織物厚度和線圈密度等結構參數對不同含水率下的織物熱阻有顯著影響。Mansoor等[32]分別在式（6）-式（8）和式（14）的理論模型基礎上，將纖維的熱導率替換為潤濕狀態下對應的數值，提出了預測汗濕狀態下襪子熱導率和熱阻的理論模型。在此基礎上提出了用于計算不同濕度、不同成分的平均纖維熱導率的修正模型：

λwet=λwvw+∑λivivw+∑vi（16）

式中：λwet是含水分纖維的平均熱導率;λw為水的熱導率;vw為水的體積分數;λi為第i種纖維的熱導率;vi為第i種纖維的體積分數。該模型雖然考慮了含水狀態對纖維熱導率的改變，但忽略了水分蒸發及纖維吸附解吸過程對織物熱傳遞性能的綜合影響。為了預測織物含水狀態下的穩態傳熱性能，Neves等[33]建立了詳細的熱濕耦合傳遞數學模型，用來分析幾種織物特性（外表面輻射系數、屈曲度和纖維比例）和纖維特性（親水性、纖維中水的擴散系數、熱導率、密度和比熱）對多層織物傳熱和傳質的影響，并通過實驗測量對織物模型中溫度和濕度的預測值進行驗證。

織物中水分的存在影響纖維導熱和織物微觀結構，進而造成織物熱導率發生變化，而織物內部的溫度分布情況又影響水分的傳遞[8]。因此，織物中水分和熱量傳遞過程相互影響，十分復雜，在進行含水織物熱傳遞性能預測時需考慮熱濕耦合作用的綜合影響。

2.2 含相變材料織物

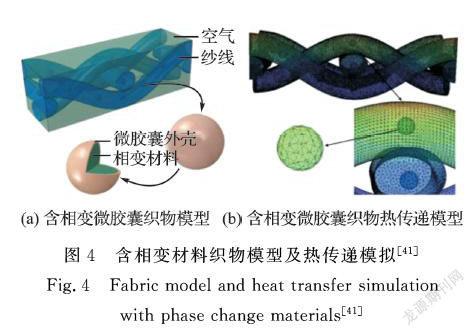
相變材料（PCM）是指在一定的熔化溫度下可以儲存或釋放大量能量的物質。PCM的熱性能為熱調節紡織品的開發提供了新的機遇，將PCM以微膠囊顆粒形式添加到紗線中或布置于織物表面，可以達到調節織物熱傳遞性能的效果[34-36]。在對含相變材料復合織物進行熱傳遞性能預測時，需要在模型中加入PCM的相變溫度、相變潛熱、熱導率等熱物性參數。李鳳志等[37]基于織物熱濕耦合模型，考慮相變微膠囊種類、微膠囊表面與織物的單位面積綜合換熱系數、微膠囊表面溫度、微膠囊在微元體中的比面積等因素，建立含PCM織物的傳熱數學模型，分析了相變微膠囊及其混合物集中分布于織物外層或織物內層以及平均分布于織物內外兩層時對織物傳熱特性的影響。朱方龍[38]構建了火災環境下含PCM的多層火災安全防護服的傳熱模型，考慮PCM的熔化熱、相變潛熱、相變層固相材料質量分數，模擬研究了多層熱防護織物（防火外層、防水汽障層及相變隔熱層）中不同的層間結構對其熱傳遞性能的影響。Jaworski[39]建立了包含PCM的多層織物傳熱數學模型。考慮了織物與環境相互作用的不同形式，包括輻射、自然對流以及織物與高熱容材料的直接接觸傳熱。通過對含PCM織物傳熱性能的實驗測試，驗證了模型的有效性。

與數學理論模型相比，有限元模型更能直觀表達含PCM復合織物傳熱過程的特點。陳旭等[40]建立了PCM涂層織物的二維傳熱模型，模型結構包含涂覆層、織物層和內環境。利用ANSYS有限元軟件模擬了低溫條件下復合織物內部各層間熱量分布情況，討論了復合織物中相變微膠囊的相變潛熱和體積分數對其低溫防護性能的影響。Iqbal等[41]采用擠出工藝將多絲聚丙烯紗線與微膠囊化PCM制成復合紗線，后制成機織物。根據相變微膠囊及織物內部實際結構，建立了含有微膠囊核殼結構的三維幾何模型，并利用有限元方法進行傳熱模擬，如圖4所示。實驗驗證結果表明，該模型可用于分析含微膠囊相變材料的不同織物和含不同量微膠囊相變材料織物的傳熱特性。但此傳熱模型僅適用于平紋組織，對于其他織物組織結構，模型需要通過實驗結果重新驗證。

3 結論與展望

對織物熱傳遞性能進行預測，可以方便快捷地獲取織物傳熱性能，更好地進行織物設計、指導相關生產、節約實驗成本，對企業生產和相關研究有一定幫助。不同的預測模型具有不同的特點及適用性，在實際應用時可以根據具體情況進行選擇。從當前研究可以看出，織物熱傳遞性能預測還有一定的發展空間。

a）基于織物內部結構參數建立織物模型，考慮織物的多相物質組成及其微觀結構特征，克服了前期均質平壁模型帶來的誤差。但當前熱傳遞模擬多基于一維穩態傳熱，今后可逐步完善多維度、非穩態傳熱條件下的織物熱傳遞模擬。

b）當前研究的織物模型的結構組成大多基于空氣和紗線，而忽略了水分存在對織物內部結構參數及熱量傳遞的影響，因此織物熱濕耦合傳遞是未來預測研究的發展方向。

c）相變材料為改善織物熱調節性能提供了新的研究思路，可通過研究相變材料調溫機制及其在織物內部不同的分布特征對織物結構與性能的影響，預測新型相變調溫織物的傳熱性能。

參考文獻：

[1]王丹，王東曉，丁一凡，等.織物特性對熱濕傳遞性能的影響[J].輕紡工業與技術，2020，49（11）：17-18.

WANG Dan， WANG Dongxiao， DING Yifan，et al. Influence of fabric property on its thermal and moisture transfer performances[J]. Light and Textile Industry and Technology， 2020， 49（11）： 17-18.

[2]高帥，龐方麗.針織物組織結構對其熱傳遞性能的影響[J].山東紡織科技，2020，61（5）：9-10.

GAO Shuai， PANG Fangli. The influence of knitted fabric structure on its heat transfer performance[J]. Shandong Textile Science & Technology，2020， 61（5）： 9-10.

[3]劉讓同，劉淑萍，李亮，等.織物結構對機織物熱傳導的影響[J].上海紡織科技，2017，45（6）：4-7.

LIU Rangtong， LIU Shuping， LI Liang，et al. Effect of fabric structure on heat conduction of woven fabrics[J]. Shanghai Textile Science & Technology， 2017， 45（6）： 4-7.

[4]張鶴譽，鄭振榮，趙曉明，等.玻璃纖維交織織物的熱傳遞數值模擬[J].紡織學報，2015，36（3）：28-31，42.

ZHANG Heyu， ZHENG Zhenrong， ZHAO Xiaoming， et al.Numerical simulation of heat transfer on glass fiber woven fabric[J]. Journal of Textile Research， 2015， 36（3）： 28-31，42.

[5]鄭振榮，張玉雙，王紅梅，等.基于紗線交織結構的織物傳熱模擬方法[J].工程熱物理學報，2016，37（9）：1918-1925.

ZHENG Zhenrong， ZHANG Yushuang， WANG Hongmei， et al. A numerical simulation on heat transfer of fabric based on the yarn interweaved structure[J]. Journal of Engineering Thermophysics， 2016， 37（9）： 1918-1925.

[6]蔡彥，楊允出，錢江瑞.基于結構參數的機織物等效熱導率數學建模[J].現代紡織技術，2021，29（2）：43-49.

CAI Yan， YANG Yunchu， QIAN Jiangrui. Conductivity of woven fabrics based on structural parameters[J]. Advanced Textile Technology，2021， 29（2）： 43-49.

[7]謝璐璐，叢杉，謝倩.多孔織物熱濕耦合模擬研究與發展趨勢[J].絲綢，2014，51（6）：41-47.

XIE Lulu， CONG Shan， XIE Qian. Simulation study on heat and moisture coupling of porous fabrics[J]. Journal of Silk， 2014， 51（6） ：41-47.

[8]王紅梅，鄭振榮，張楠楠，等.多孔纖維織物熱濕傳遞數值模擬的研究進展[J].紡織學報，2016，37（11）：159-165.

WANG Hongmei， ZHENG Zhenrong， ZHANG Nannan， et al. Research progress of numerical simulation on heat and moisture transfer in porous textiles[J]. Journal of Textile Research， 2016， 37（11）： 159-165.

[9]BHATTACHARJEE D， KOTHARI VK. Measurement of thermal resistance of woven fabrics in natural and forced convections[J]. Research Journal of Textile and Apparel， 2008， 12（2）： 39-49.

[10]AFZAL A， HUSSAIN T， MOHSIN M， et al. Statistical models for predicting the thermal resistance of polyester/cotton blended interlock knitted fabrics[J]. International Journal of Thermal Sciences， 2014， 85： 40-46.

[11]崔巖，盧昀坤，曹雷剛，等.面向材料基因工程的人工神經網絡研究[J].熱加工工藝，2018，47（12）：13-16.

CUI Yan， LU Yunkun， CAO Leigang， et al. Research on artificial neural network for material genetic engineering[J]. Hot Working Technology，2018， 47（12）： 13-16.

[12]康靚，米曉希，王海蓮，等.人工神經網絡在材料科學中的研究進展[J].材料導報，2020，34（21）：21172-21179.

KANG Jing， MI Xiaoxi， WANG Hailian， et al. Research progress of artificial neural networks in material science[J]. Materials Reports， 2020， 34（21）： 21172-21179.

[13]MAJUMDAR A. Modelling of thermal conductivity of knitted fabrics made of cotton-bamboo yarns using artificial neural network[J]. Journal of the Textile Institute， 2011， 102（9）： 752-762.

[14]GUENESOGLU S， KAPLANGIRAY B. Applying the artifical neural network to predict the thermal properties of knitted fabrics[J]. Vlakna a Textile， 2019， 26（1）： 41-44.

[15]ALIBI H， FAYALA F， JEMNI A， et al. Modeling of thermal conductivity of stretch knitted fabrics using an optimal neural networks system[J]. Journal of Applied Sciences， 2012， 12（22）： 2283-2294.

[16]LEVY F L. A modified Maxwell-Eucken equation for calculating the thermal conductivity of two-component solutions or mixtures[J]. International Journal of Refrigeration， 1981， 4（4）： 223-225.

[17]BOGATY H， HOLLIES N R S， HARRIS M. Some Thermal Properties of Fabrics[J]. Textile Research Journal， 1957， 27（6）： 445-449.

[18]MAXWELL J C. A treatise on electricity and magnetism[J]. Nature， 1873， 7（182）： 478-480.

[19]EUCKEN A. Allgemeine gesetzmigkeiten für das wrmeleitvermgen verschiedener stoffarten und aggregatzustnde[J]. Forschung Auf Dem Gebiet Des Ingenieurwesens A， 1940， 11（1）：6-20.

[20]HALAOUA S， ROMDHANI Z， JEMNI A. Effect of textile woven fabric parameters on its thermal properties[J]. Industria Textila， 2019， 70（1）：15-20.

[21]SEO B H， CHO Y J， YOUN J R， et al. Model for thermal conductivities in spun yarn carbon fabric composites[J]. Polymer Composites， 2005， 26（6）： 791-798.

[22]WANG J F， CARSON J K， NORTH M F， et al. A new structural model of effective thermal conductivity for heterogeneous materials with co-continuous phases[J]. International Journal of Heat and Mass Transfer， 2008， 51（9-10）： 2389-2397.

[23]KOTHARI V K， BHATTACHARJEE D. Prediction of thermal resistance of woven fabrics. Part I： Mathematical model[J]. Journal of the Textile Institute， 2008， 99（5）： 421-432.

[24]WEI J， XU S J， LIU H， et al. Simplified model for predicting fabric thermal resistance according to its microstructural parameters[J]. Fibres & Textiles in Eastern Europe， 2015， 23（4）： 57-60.

[25]SIDDIQUI M O R， SUN D M. Finite element analysis of thermal conductivity and thermal resistance behaviour of woven fabric[J]. Computational Materials Science， 2013， 75： 45-51.

[26]SUN Y C， CHEN X G， CHENG Z H， et al. Study of heat transfer through layers of textiles using finite element method[J]. International Journal of Clothing Science and Technology， 2010， 22（2/3）： 161-173.

[27]ZHENG Z R， ZHANG N N， ZHAO X M. Simulation of heat transfer through woven fabrics based on the fabric geometry model[J]. Thermal Science， 2018， 22： 2815-2825.

[28]張潔，劉新金，謝春萍，等.織物結構參數對熱傳遞性能影響的模擬分析[J].絲綢，2020，57（2）：13-18.

ZHANG Jie， LIU Xinjin， XIE Chunping， et al. Simulation analysis of the influence of fabric structure parameters on heat transfer properties[J]. Journal of Silk， 2020， 57（2）： 13-18.

[29]蔡彥，陳怡充，嚴航宇，等.織物接觸冷暖感的模擬分析[J].毛紡科技，2020，48（5）：97-102.

CAI Yan， CHEN Yichong， YAN Hangyu， et al. Simulation analysis of the contact warm-cool feeling of fabric[J]. Wool Textile Journal，2020， 48（5）： 97-102.

[30]WU J J， TANG H， WU Y X. A predictive model of thermal conductivity of plain woven fabrics[J]. Thermal Science， 2017， 21（4）： 1627-1632.

[31]KANAT Z E， ZDIL N， MARMARALI A. Prediction of thermal resistance of the knitted fabrics in wet state by using multiple regression analysis[J]. Tekstil VeKonfeksiyon， 2014， 24（3）：291-297.

[32]MANSOOR T， HES L， BAJZIK V. A new approach for thermal resistance prediction of different composition plain socks in wet state （Part 2）[J]. Autex Research Journal， 2020，21（2）：238-247.

[33]NEVES S F， CAMPOS J B L M， MAYOR T S. Effects of clothing and fibres properties on the heat and mass transport， for different body heat/sweat releases[J]. Applied Thermal Engineering， 2017， 117：109-121.

[34]孫潔，孫娜，周建安，等.相變微膠囊及其功能紡織品研究進展[J].服裝學報，2019，4（3）：189-200.

SUN Jie， SUN Na， ZHOU Jian'an， et al. Research and development of phase change material microcapsules and functional textiles[J]. Journal of Clothing Research， 2019， 4（3）： 189-200.

[35]朱雯，蘇云，陳若穎，等.相變微膠囊涂層織物在熱防護服中的應用[J].中國安全科學學報，2020，30（12）：180-185.

ZHU Wen， SU Yun， CHEN Ruoying， et al. Application of fabric coated with phase change microcapsule in thermal protective clothing[J]. China Safety Science Journal，2020， 30（12）： 180-185.

[36]肖堯，余弘，李衛東，等.相變調溫紡織品研究現狀及評價方法[J].紡織檢測與標準，2019，5（4）：1-5.

XIAO Yao， YU Hong， LI Weidong， et al. Research status and evaluation method of phase change thermostat textiles[J]. Textile Testing and Standard，2019， 5（4）： 1-5.

[37]李鳳志，朱云飛，王鵬飛，等.織物-多種相變微膠囊復合材料熱特性數值模擬[J].南京航空航天大學學報，2009，41（4）：456-460.

LI Fengzhi， ZHU Yunfei， WANG Pengfei， et al. Numerical simulation on thermal properties of textile with multi-type PCM microcapsules[J]. Journal of Nanjing University of Aeronautics & Astronautics，2009， 41（4）： 456-460.

[38]朱方龍.附加相變材料層的熱防護服裝傳熱數值模擬[J].應用基礎與工程科學學報，2011，19（4）：635-643.

ZHU Fanglong. Numerical simulation of heat transfer for thermal protective clothing incorporating phase change material layer[J]. Journal of Basic Science and Engineering，2011， 19（4）： 635-643.

[39]JAWORSKI M. Mathematical model of heat transfer in PCM incorporated fabrics subjected to different thermal loads[J]. Applied Thermal Engineering， 2019， 150： 506-511.

[40]陳旭，吳炳洋，范瀅，等.蓄熱調溫織物低溫防護過程的數值模擬[J].紡織學報，2019，40（7）：163-168.

CHEN Xu， WU Bingyang， FAN Ying， et al. Numerical simulation of low temperature protection process for heat storage fabrics[J]. Journal of Textile Research， 2019， 40（7）： 163-168.

[41]IQBAL K， SUN D M， STYLIOS G K， et al. FE analysis of thermal properties of woven fabric constructed by yarn incorporated with microencapsulated phase change materials[J]. Fibers and Polymers， 2015， 16（11）：2497-2503.