評(píng)估織物懸垂性的新方法
RYKLINDzmitry РыклинДмитрийБорисович 湯曉彤

摘 要:為了開發(fā)評(píng)估織物懸垂性的新方法,建立了描述懸垂織物的數(shù)學(xué)模型,用以描述織物的懸垂外觀形態(tài),并提出了評(píng)估織物懸垂性的新指標(biāo)。選取6塊平紋亞麻織物,在現(xiàn)有的織物懸垂性能測(cè)試儀器的基礎(chǔ)上,引入3D掃描儀,獲得了懸垂織物三維圖像及數(shù)據(jù),并對(duì)所獲得數(shù)據(jù)進(jìn)行統(tǒng)計(jì)處理得出評(píng)估結(jié)果。結(jié)果表明:新開發(fā)的數(shù)學(xué)模型可以精確地描述不同亞麻織物的懸垂外觀形態(tài),通過對(duì)不同平紋亞麻織物測(cè)試和數(shù)據(jù)分析,證實(shí)了新方法具有較高的準(zhǔn)確性,相比于傘式法,該方法可以更為有效地評(píng)估織物的懸垂形態(tài)。
關(guān)鍵詞:懸垂性;平紋亞麻織物;3D掃描;彎曲剛度
中圖分類號(hào):TS127
文獻(xiàn)標(biāo)志碼:A
文章編號(hào):1009-265X(2022)01-0109-06
Abstract: In order to establish a new method for evaluating the drapability of fabrics, a mathematical model describing the drapability of fabrics was developed, and a new index was presented to evaluate the drapability of fabrics. Six pieces of plain linen fabrics were selected. Based on the existing testing instrument for the drapability of fabrics, a 3D scanner was introduced to obtain the 3D images and data of draping fabrics and the data obtained were statistically processed to get evaluation results. The results show that the newly developed mathematical model can accurately describe the draping appearance of different linen fabrics. The test and data analysis of different plain linen fabrics confirm that the new method has higher accuracy. Compared with the umbrella method, this method can evaluate the draping morphologies of fabrics in a more effective way.
Key words: drapability; plain linen fabric; 3D scanning; bending stiffness
懸垂性是織物的主要性能之一,該性能可以直接決定其制成產(chǎn)品的外觀形態(tài)。從1930年開始,國內(nèi)外學(xué)者們對(duì)織物懸垂性的研究一直持續(xù)至今。為了科學(xué)地判斷織物的懸垂性能,其評(píng)估方法的開發(fā)也受到了各國學(xué)者的廣泛關(guān)注[1-3]。懸垂性是織物在自身重量的影響下自然下垂,從而形成優(yōu)美褶皺的能力[4]。從該定義可以看出,織物在懸垂?fàn)顟B(tài)下的外觀形態(tài)及其美感程度是評(píng)估懸垂性的主要依據(jù)。
根據(jù)GB/T 23329-2009《紡織品 織物懸垂性的測(cè)定》可知,評(píng)估織物懸垂性的普遍方法是傘式法,評(píng)估指標(biāo)主要為懸垂系數(shù)。該指標(biāo)是取自織物在懸垂?fàn)顟B(tài)下形成的褶皺投影及其外輪廓線的信息,并沒有考慮在懸垂?fàn)顟B(tài)下織物表面的整體形態(tài)。基于對(duì)科學(xué)文獻(xiàn)的分析,可以發(fā)現(xiàn),具有相同懸垂系數(shù)值的不同織物,其懸垂形態(tài)差異較大,并且它們的褶皺形狀可能相同也可能是完全不同的[5]。因此,
可以說懸垂系數(shù)這一指標(biāo)不足以完全評(píng)估織物的懸垂性。通過對(duì)已有文獻(xiàn)的歸納還可以確定的是,采用3D掃描技術(shù)的研究方法是完善評(píng)估織物懸垂性方法中最有前景的方向之一,因?yàn)?D掃描儀可以提供有關(guān)懸垂織物形態(tài)的準(zhǔn)確信息,因此各國的學(xué)者都在積極地嘗試應(yīng)用3D掃描技術(shù)來開發(fā)評(píng)估織物懸垂性的方法[6-9]。然而,當(dāng)前已存在的評(píng)估方法尚未充分開發(fā)出表征織物懸垂形態(tài)和描述褶皺形狀的復(fù)雜指標(biāo)。
亞麻織物是中國的重要出口產(chǎn)品,在全球亞麻面料的出口份額中,中國出口量?jī)H次于意大利。亞麻織物具有許多良好的材料性能,如高強(qiáng)度、高吸濕性、低過敏性和快速高溫調(diào)節(jié)性能。同時(shí),亞麻織物也有許多不足,其中最主要的性能缺點(diǎn)為高剛性和低懸垂性。擴(kuò)展亞麻面料的應(yīng)用范圍、提高產(chǎn)品質(zhì)量是提升其在國際市場(chǎng)競(jìng)爭(zhēng)力的主要途徑。因此,準(zhǔn)確鑒定亞麻織物的各項(xiàng)性能是十分必要的。
本文選擇以亞麻織物作為研究對(duì)象,重新建立數(shù)學(xué)模型及相應(yīng)的評(píng)價(jià)指標(biāo)來評(píng)估懸垂織物的整體外觀形態(tài),嘗試對(duì)織物的懸垂性能建立一種更為有效的評(píng)估方法和評(píng)價(jià)指標(biāo)。
1 理論分析及模型設(shè)定
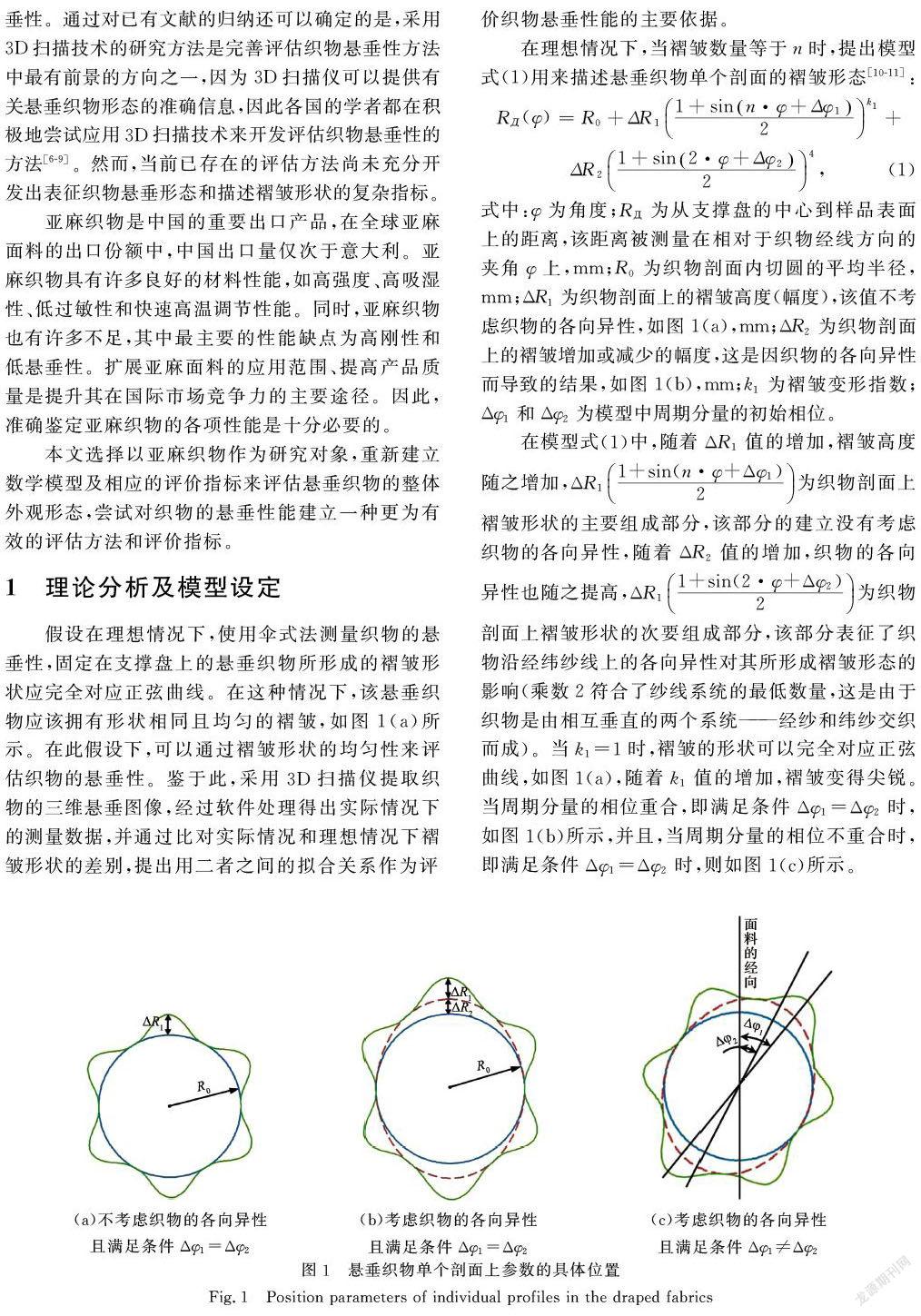
假設(shè)在理想情況下,使用傘式法測(cè)量織物的懸垂性,固定在支撐盤上的懸垂織物所形成的褶皺形狀應(yīng)完全對(duì)應(yīng)正弦曲線。在這種情況下,該懸垂織物應(yīng)該擁有形狀相同且均勻的褶皺,如圖1(a)所示。在此假設(shè)下,可以通過褶皺形狀的均勻性來評(píng)估織物的懸垂性。鑒于此,采用3D掃描儀提取織物的三維懸垂圖像,經(jīng)過軟件處理得出實(shí)際情況下的測(cè)量數(shù)據(jù),并通過比對(duì)實(shí)際情況和理想情況下褶皺形狀的差別,提出用二者之間的擬合關(guān)系作為評(píng)價(jià)織物懸垂性能的主要依據(jù)。
在理想情況下,當(dāng)褶皺數(shù)量等于n時(shí),提出模型式(1)用來描述懸垂織物單個(gè)剖面的褶皺形態(tài)[10-11]:
RД(φ)=R0+ΔR11+sinn·φ+Δφ12k1+
ΔR21+sin2·φ+Δφ224,(1)
式中:φ為角度;RД為從支撐盤的中心到樣品表面上的距離,該距離被測(cè)量在相對(duì)于織物經(jīng)線方向的夾角φ上,mm;R0為織物剖面內(nèi)切圓的平均半徑,mm;ΔR1為織物剖面上的褶皺高度(幅度),該值不考慮織物的各向異性,如圖1(a),mm;ΔR2為織物剖面上的褶皺增加或減少的幅度,這是因織物的各向異性而導(dǎo)致的結(jié)果,如圖1(b),mm;k1為褶皺變形指數(shù);Δφ1和Δφ2為模型中周期分量的初始相位。
在模型式(1)中,隨著ΔR1值的增加,褶皺高度隨之增加,ΔR11+sin(n·φ+Δφ1)2為織物剖面上褶皺形狀的主要組成部分,該部分的建立沒有考慮織物的各向異性,隨著ΔR2值的增加,織物的各向異性也隨之提高,ΔR11+sin(2·φ+Δφ2)2為織物剖面上褶皺形狀的次要組成部分,該部分表征了織物沿經(jīng)緯紗線上的各向異性對(duì)其所形成褶皺形態(tài)的影響(乘數(shù)2符合了紗線系統(tǒng)的最低數(shù)量,這是由于織物是由相互垂直的兩個(gè)系統(tǒng)——經(jīng)紗和緯紗交織而成)。當(dāng)k1=1時(shí),褶皺的形狀可以完全對(duì)應(yīng)正弦曲線,如圖1(a),隨著k1值的增加,褶皺變得尖銳。當(dāng)周期分量的相位重合,即滿足條件Δφ1=Δφ2時(shí),如圖1(b)所示,并且,當(dāng)周期分量的相位不重合時(shí),即滿足條件Δφ1=Δφ2時(shí),則如圖1(c)所示。
在理想情況下,當(dāng)褶皺數(shù)量等于n時(shí),懸垂織物的整體外觀形態(tài)可以用模型式(2)來表示[11]:
RД(φ,H)=(a0+a1·H)+(a2+a3·H)1+sin(n·φ+Δφ1)2(a4+a5·H)+(a6+a7·H)1+sin2·φ+Δφ224,(2)
式中:H為懸垂織物表面到支撐盤的距離,mm;a0~a7為經(jīng)驗(yàn)系數(shù)。
在模型式(1)中,經(jīng)驗(yàn)系數(shù)a0~a7的值取決于實(shí)驗(yàn)測(cè)試過程的參數(shù)(如樣品半徑、支撐盤的半徑)和測(cè)試織物的特性(如表面密度,經(jīng)緯密度,經(jīng)緯線剛度,編織等)。通過模型式(2),可以確定試樣面料表面上每個(gè)點(diǎn)的位置,這主要取決于距離H和經(jīng)紗方向與線段之間所構(gòu)成的夾角φ。
通過數(shù)學(xué)模型式(1)的數(shù)據(jù)處理可以得出指標(biāo)R21,該指標(biāo)用來表征懸垂織物在距離H下的單個(gè)(一個(gè))剖面褶皺形狀的擬合程度,擬合程度越高,則剖面褶皺形狀的均勻度越高。通過數(shù)學(xué)模型式(2)的數(shù)據(jù)處理可以得出指標(biāo)R22,該指標(biāo)用來表征懸垂織物整體形態(tài)的擬合程度,是10~25mm之間每毫米的剖面按順序疊加起來的懸垂織物整體形態(tài),即26個(gè)剖面褶皺形狀擬合系數(shù)的平均值,擬合程度越高,懸垂織物的整體外觀形態(tài)越美觀。剖面褶皺形狀的均勻度包涵在懸垂織物整體形態(tài)之中,所以,可以說指標(biāo)R22涵蓋了指標(biāo)R21,但指標(biāo)R22并不能完全替代指標(biāo)R21。
擬合系數(shù)R21和R22的值越接近1,表示數(shù)學(xué)模型的擬合性越高,說明該懸垂織物的褶皺形狀越均勻,懸垂織物的整體外觀形態(tài)越美觀,即織物的懸垂性也就越高,反之,則表示懸垂性差。
2 實(shí) 驗(yàn)
2.1 實(shí)驗(yàn)材料
選擇6塊平紋亞麻織物作為研究的對(duì)象,其規(guī)格參數(shù)見表1。表1中的懸垂系數(shù)值是按照標(biāo)準(zhǔn)GB/T 23329-2009《紡織品 織物懸垂性的測(cè)定》的公式來計(jì)算的,其評(píng)價(jià)準(zhǔn)則應(yīng)為懸垂系數(shù)值越低,則懸垂性越高。
2.2 儀器設(shè)備
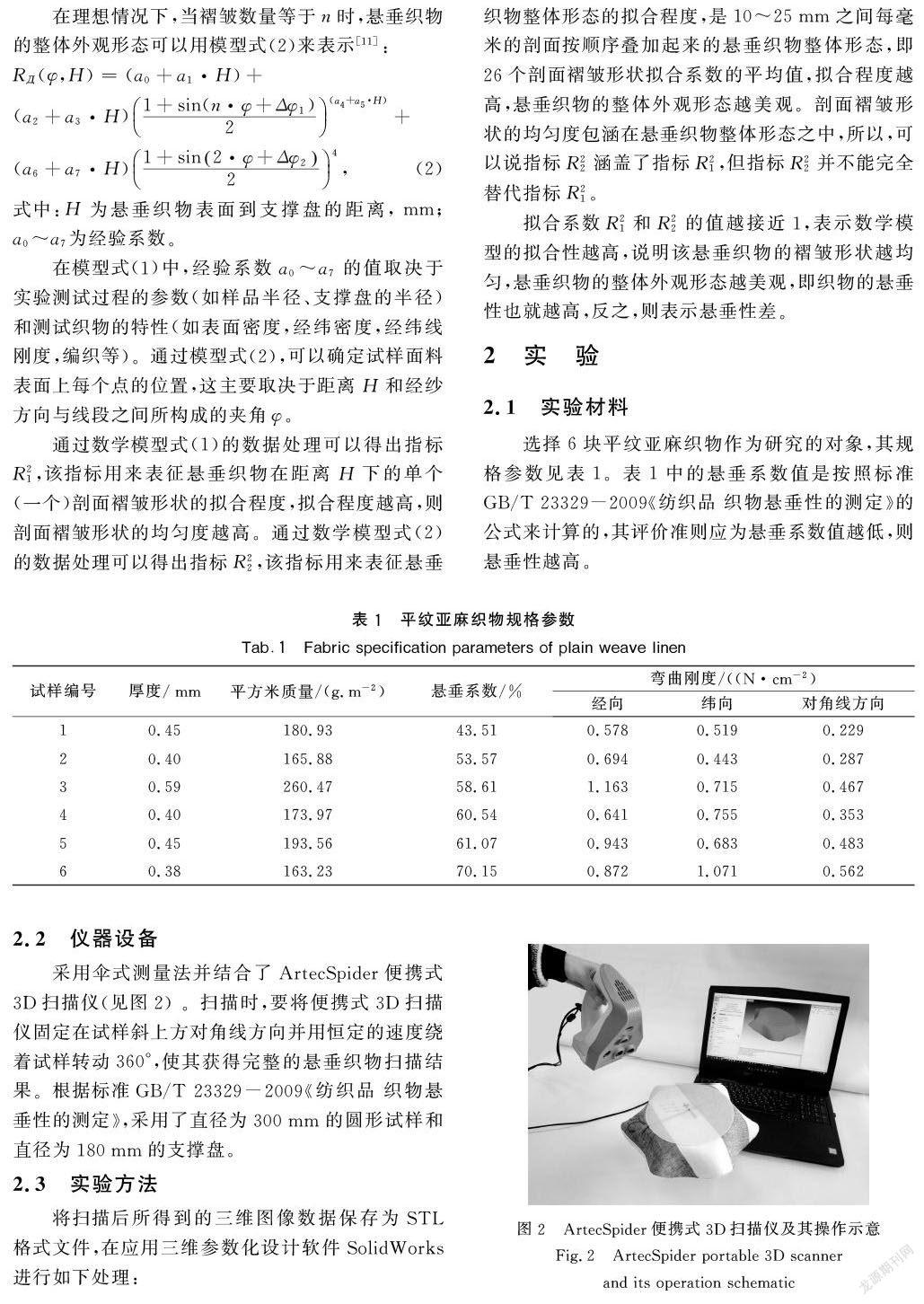
采用傘式測(cè)量法并結(jié)合了ArtecSpider便攜式3D掃描儀(見圖2) 。掃描時(shí),要將便攜式3D掃描儀固定在試樣斜上方對(duì)角線方向并用恒定的速度繞著試樣轉(zhuǎn)動(dòng)360°,使其獲得完整的懸垂織物掃描結(jié)果。根據(jù)標(biāo)準(zhǔn)GB/T 23329-2009《紡織品 織物懸垂性的測(cè)定》,采用了直徑為300mm的圓形試樣和直徑為180mm的支撐盤。
2.3 實(shí)驗(yàn)方法
將掃描后所得到的三維圖像數(shù)據(jù)保存為STL格式文件,在應(yīng)用三維參數(shù)化設(shè)計(jì)軟件SolidWorks進(jìn)行如下處理:
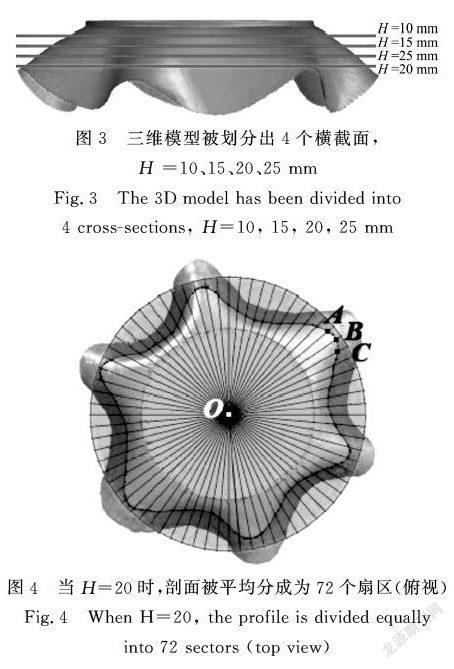
a)在獲得的懸垂三維模型(正視圖)上劃分出4個(gè)平行截面,該截面到支撐盤的距離分別為10、15、20、25mm(圖3),該距離的設(shè)定取決于試樣下垂部分的高度;
b)將每個(gè)剖面平均分為72個(gè)扇形部分,每個(gè)扇形的中心角度為5(見圖4);
c)對(duì)于每個(gè)扇形部分,都要確定從支撐盤中心O點(diǎn)到懸垂織物表面上交匯點(diǎn)的距離,如A、B、C點(diǎn)等以此類推,所以每個(gè)截面分別要獲取72個(gè)數(shù)據(jù)結(jié)果(見圖4)。
3 結(jié)果與討論
通過3D掃描儀所獲取的懸垂織物表面形態(tài)的三維圖像如圖5所示。
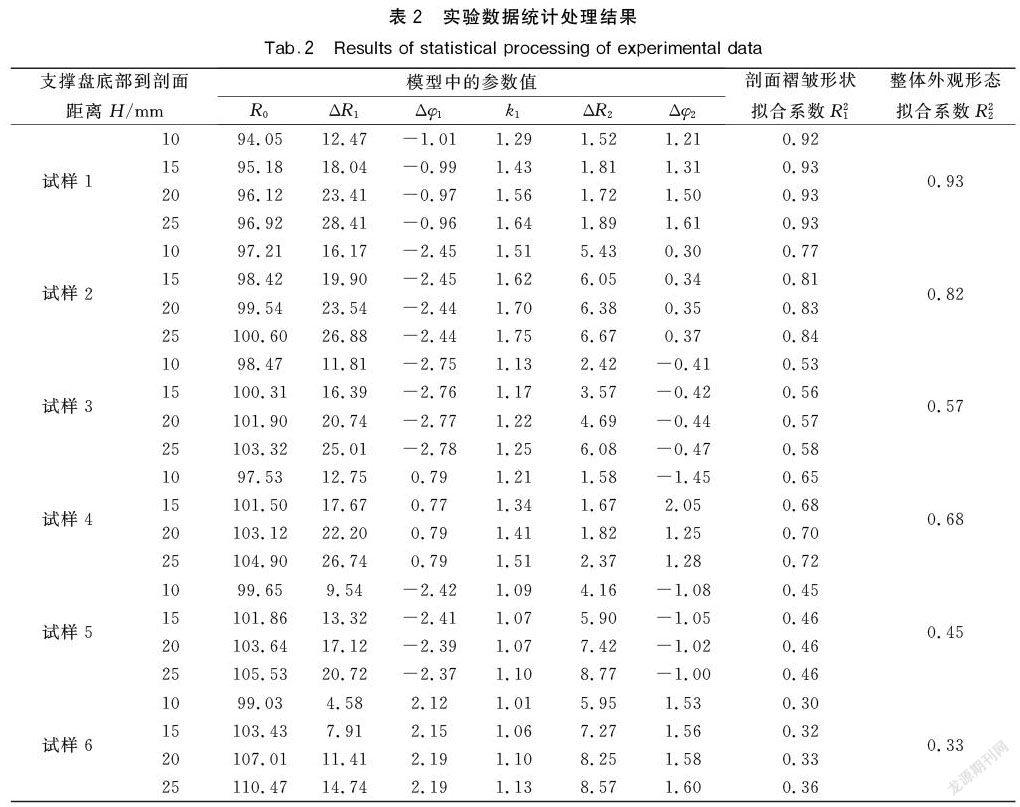
將已獲取的三維掃描數(shù)據(jù)通過統(tǒng)計(jì)軟件Statistica帶入到模型式(1)和式(2)中進(jìn)行擬合計(jì)算,處理結(jié)果見表2。
分析懸垂織物試樣的三維圖像5(a)—(f)和實(shí)驗(yàn)數(shù)據(jù)統(tǒng)計(jì)處理結(jié)果表2,可以發(fā)現(xiàn):
a)剖面褶皺形狀擬合系數(shù)R21的值隨著支撐盤到剖面距離H的增加而提高,這表明,所測(cè)量的懸垂剖面距離支撐盤越遠(yuǎn),其結(jié)果受支撐盤的影響就越小,試樣也就越容易形成均勻的褶皺。這也說明了支撐盤到剖面距離H的值越大,其測(cè)量的準(zhǔn)確性就越高。
b)1號(hào)試樣的懸垂褶皺形狀是所有圖像中最均勻的,其相對(duì)應(yīng)剖面褶皺形狀擬合系數(shù)R21的值也比較高,在0.93~0.92之間。并且,其整體外觀形態(tài)擬合系數(shù)R22的值也是最高的,為0.93,說明1號(hào)試樣的懸垂性是所有試樣中最好的。
c)2號(hào)試樣三維圖像的懸垂褶皺形狀也比較均勻。系數(shù)R21的值在0.77~0.84之間,系數(shù)R22值為0.82,僅次于1號(hào)試樣,這說明2號(hào)試樣的懸垂性僅次于1號(hào)試樣。
d)由6號(hào)試樣的三維圖像可以明顯看出,其懸垂褶皺形狀最不均勻。系數(shù)R21的值僅在0.30~0.36之間,系數(shù)R22值也是最低的,為0.33,說明6號(hào)試樣懸垂性是所有試樣中最差的。
e)3、4、5號(hào)試樣的三維圖像具有較大的差異性,3和5號(hào)試樣的懸垂褶皺形狀不均勻,相比它們4號(hào)試樣卻較為均勻。這3個(gè)試樣的懸垂系數(shù)值分別為57.61,60.54 和61.07,都比較相近,很難做出明確的區(qū)分。然而,通過新方法所得到的系數(shù)R22值為:3號(hào)-0.57、4號(hào)-0.68,5號(hào)-0.45。由此可見,系數(shù)R22值可以直觀地獲得具有相似懸垂系數(shù)值的不同織物之間正確的懸垂性比對(duì)關(guān)系,并且該指標(biāo)的比對(duì)結(jié)果完全符合直觀的三維圖像結(jié)果。
f)在排除2號(hào)試樣的情況下,所有試樣的ΔR2值都是隨著系數(shù)R21值的增加而降低,也就是說,剖面褶皺形狀的均勻度隨著織物各向異性的增加而下降。并且,在對(duì)比織物規(guī)格參數(shù)和實(shí)驗(yàn)數(shù)據(jù)統(tǒng)計(jì)處理結(jié)果時(shí),發(fā)現(xiàn),隨著織物對(duì)角線方向(45°)上彎曲剛度的降低其系數(shù)R22的值也在提高。在徐軍等[12]的文章中也有類似的發(fā)現(xiàn),他們認(rèn)為織物在彎曲時(shí)存在明顯的各向異性,且織物在對(duì)角線方向(45°)上的彎曲剛度是最小的,因此可以說它對(duì)褶皺形成的影響是最大的。導(dǎo)致2號(hào)試樣的各向異性值比較高的原因可能是由于該織物經(jīng)緯向上的彎曲剛度的差異略大。
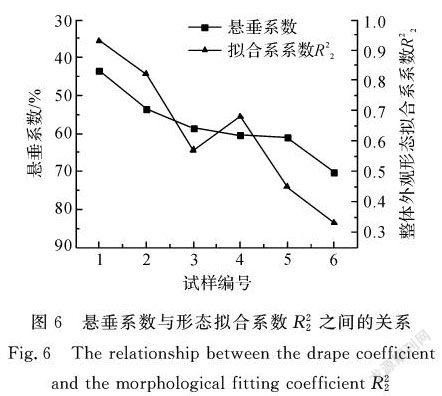
圖6為懸垂系數(shù)與整體外觀形態(tài)擬合系數(shù)R22的變化趨勢(shì)關(guān)系。由圖6可知,這兩種系數(shù)的指標(biāo)結(jié)果其整體變化趨勢(shì)基本一致。1號(hào)試樣懸垂系數(shù)最低,系數(shù)R22值最高,而6號(hào)試樣的懸垂系數(shù)最高,系數(shù)R22值也最低,這說明該指標(biāo)的評(píng)價(jià)結(jié)果具有較高的可行性。盡管,4號(hào)試樣和5號(hào)試樣的懸垂系數(shù)結(jié)果非常相近,但4號(hào)試樣的整體外觀形態(tài)擬合系數(shù)R22值卻明顯高于3號(hào)試樣。對(duì)比織物的三維圖像,也可以發(fā)現(xiàn)相同的評(píng)價(jià)結(jié)果。與傘式法相比,新方法的測(cè)量結(jié)果更加符合三維圖像的直接觀測(cè)結(jié)果,尤其是當(dāng)不同試樣之間的懸垂系數(shù)值較為接近時(shí)。
4 結(jié) 論
不同的亞麻織物所得到的褶皺形態(tài)剖面擬合系數(shù)R21和整體外觀形態(tài)擬合系數(shù)R22的結(jié)果符合其三維圖像的對(duì)應(yīng)關(guān)系。這證實(shí)了,新方法所提出的數(shù)學(xué)模型可以正確描述不同亞麻平紋織物的懸垂外觀形態(tài)。
因此,可以確定的是,評(píng)估懸垂性的新方法具有較高的準(zhǔn)確性。與傘式方法相比,在織物懸垂性差異較小的情況下或者是當(dāng)織物所測(cè)得的懸垂系數(shù)結(jié)果較為接近時(shí),新方法可以更為有效地評(píng)價(jià)織物的懸垂性。除此之外,從數(shù)學(xué)模型式(1)和式(2)中還獲得了其他的參數(shù)指標(biāo),這些參數(shù)指標(biāo)還有待進(jìn)一步研究和驗(yàn)證。
參考文獻(xiàn):
[1]SANAD R, CASSIDY T, VIEN C, Evans E. Fabric and garment drape measurement Part 2[J]. Journal of Fiber Bioengineering and Informatics, 2013, 6(1): 1-22.
[2]TSAI K H, TSAI M C, WANG P N, et al. New approach to directly acquiringe the drape contours of various fabrics[J]. Fibres & Textiles in Eastern Europe, 2009, 17(3): 54-59.
[3]GNANAVEL P, ANANTHAKRISHNAN T. Volume based measurement of fabric drape using surfer software and studies on effect of influencing factors[J]. Journal of Textile Science & Engineering, 2014, 4(4): 159.
[4]姚穆.紡織材料學(xué)[M].北京:中國紡織出版社,1980:383.
YAO Mu.Textile Materials[M]. Beijing: China Textiles Press, 1980: 383.
[5]CARRERA-GALLISSà E, CAPDEVILA X, VALL-DEPERAS J. Evaluating drape shape in woven fabrics[J]. Journal of the Textile Institute, 2017, 108(3): 325-336.
[6]GLOMBIKOVA V, KUS Z. Drape evaluation by the 3D drape scanner[J]. Tekstil ve konfeksiyon, 2014, 24(3): 279-285.
[7]沈偉,任靜,周華,等.基于Kinect傳感器的織物懸垂性測(cè)試[J].2014,31(5):306-309,328.
SHEN Wei, REN Jing, ZHOU Hua, et al. Fabric drape measurement method based on kinect sensor[J]. Journal of Zhejiang Sci-Tech University, 2014, 31(5): 306-309, 328.
[8]張曉婷,洪劍寒,查神愛,等.基于三維掃描技術(shù)的毛織物懸垂性能測(cè)試方法[J].毛紡科技,2015,43(10):58-61.
ZHANG Xiaoting, HONG Jianhan, ZHA Shen'ai, et al. Study on the drape performance testing method of wool fabric with three-dimensional scanner[J]. Wool Textile Journal, 2015, 43(10): 58-61.
[9]YU Z C, ZHONG Y Q, GONG R H, et al. New indicators on fabric drape evaluation based on three-dimensional model[J]. Textile Research Journal, 2020, 90(11/12): 1291-1300.
[10]РЫКЛИН Д Б, ТАН С, ГРИШАЕВ А Н, ПЕСКОВСКИЙ Д В. Разработка математической модели драпированной ткани с использованием данных, получаемых в процессе 3D-сканирования[J]. Вестник Витебского государственного технологического университета, 2018, 1(34): 70-78.
RYKLIN D B, TANG X, GRISHAEV A, et al. Development of mathematical model of draped fabric with use of 3-d scanning data[J]. Vestnik of Vitebsk State Technological University, 2018, 1(34): 70-78.
[11]РЫКЛИН Д Б, ТАН С. Оценка анизотропии драпируемости тканей на основе анализа результатов 3D-сканирования[J]. Известия высших учебных заведений. Технология текстильной промышленности, 2020, 2(386): 137-145.
RYKLIN D B, TANG Х. Evaluation of fabrics dreapeability anisotropy on the base of 3d-scanning results analysis[J]. Higher Education Institutions Textile Industry Technology, 2020, 2(386): 137-145.
[12]徐軍,姚穆.織物彎曲剛度各向異性探討[J].西北紡織工學(xué)院學(xué)報(bào),2001,15(2):102-104,135.
XU Jun, YAO Mu. Discussion on bending rigidity anisotropy of fabrics[J]. Journal of Northwest Institute of Textile Science and Technology, 2001, 15(2): 102-104, 135.

