路面識別技術在路噪主動控制降噪性能優化中的應用

徐格格，呂 曉，史晨路，朱玉剛，鄭森

(1.河北工業大學 機械工程學院， 天津 300401；2.中汽研(天津)汽車工程研究有限公司， 天津 300300)

近年來，隨著神經網絡技術在路面識別領域的發展，越來越多學者將其成果運用到研究中。劉秋等[1]針對傳統路面識別方法不能準確識別多種路面類型的問題，運用卷積神經網絡識別路面，根據懸架系統在不同路面下的輸出響應調節控制器參數，從而使可控懸架在不同路面下均能保持性能最優。王國微等[2]為使電動汽車具有較好的制動安全性，充分利用路面附著力，運用RBF神經網絡識別路面，確定目標參數為識別出的最優滑移率，并設計出一種ABS控制策略將模糊控制和預測控制相結合。實例樣車仿真結果表明提高了回收的制動能量。Zhu等[3]為解決瞬態路面下可控懸架的延遲問題，提出了一種結合監督式深度學習的預測控制方法，建立整車模型，采用有監督的深度學習(Y0LOv3)來識別瞬態道路，為半主動懸架實現提前預判，進而有效提高車輛乘坐舒適性。

鑒于此，將采用神經網絡技術的路面識別方法與路噪主動控制相結合，通過安裝在車身上的攝像頭采集路面圖像數據，運用卷積神經網絡(CNN)識別3種不同路面類型。根據已建立的路噪模型進行仿真，找到3種路面對應的最優收斂因子。根據道路識別結果，調整不同道路下路噪主動控制系統的收斂因子，優化車輛降噪效果。

1 路噪主動控制

1.1 噪聲主動控制原理

有源噪聲控制(ANC)[4]的原理是聲波的楊氏干涉原理。在規定區域內有意地增加1個次級聲源，控制主要噪聲信號。根據2種聲波的抵消干擾條件，如果2種聲信號的聲波振幅相等，具有相反的相位，則2種聲波會在空間中進行抵消，產成消聲的“靜區”，進而實現主動降噪。這種現象稱為聲波干擾消除[5]。

設入射聲波為

p1=Acos(ωt-φ)

(1)

式中：p1表示瞬時聲壓值；A表示聲壓幅值；ω表示聲波的頻率；φ表示相位值。入射的平均聲能密度E1為

(2)

式中：ρ表示介質的密度；c表示聲波在空氣中的傳播速度；A表示聲波的振幅。次級聲信號p2為：

p2=βAcos(ωt-φ+α)

(3)

則疊加后的聲能密度E2為：

(4)

式中：α是2種聲波之間的相位差；β是2種聲波振幅的比值。則在空氣中任意一點，疊加前后2種聲波之間的聲級差Δ為：

(5)

由式(5)可知，當2種聲波的振幅相同時，β趨近1，2種聲波具有相反的相位，即α接近π時，由于與次級聲信號相互抵消，初級噪聲信號被大大衰減，即ANC技術的理論基礎。

1.2 噪聲主動控制算法

1.2.1最小均方算法

在實踐中，很難直接計算自相關矩陣來獲得最優權重系數，通常采用最小均方(LMS)算法[6-7]獲得最佳權重系數。LMS算法是一種簡單、有效的遞推方法。基于最小均方誤差算法的自適應濾波原理如圖1所示。

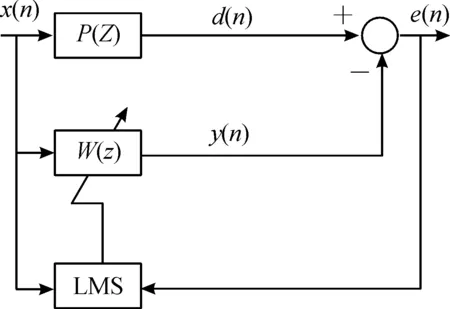
圖1 自適應濾波原理框圖

LMS算法的目標函數表示為：

J(n)=E[e2(n)]=E[(d(n)-y(n))2]

(6)

式中：y(n)為輸出信號；d(n) 為期望信號；e(n) 為誤差信號。n時刻濾波器的輸出可表示為y(n)。

(7)

將式(7)代入式(6)得到：

J(n)=E[(d(n)-WTX(n))2]

(8)

其中：

e2(n)=(d(n)-WT(n)X(n))*

(d(n)-WT(n)X(n))T

(9)

將式(9)代入式(8)中，目標函數可表示為：

J(n)=E[d2(n)]-2WT(n)P+WT(n)QW(n)

(10)

式中，P是d(n)和X(n)之間的互相關矩陣，可表示為：

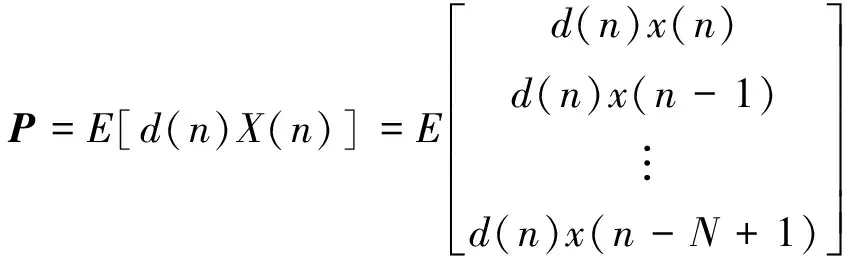
(11)

Q是X(n)的自相關矩陣，表示為：

Q=E[X(n)XT(n)]

(12)

根據式(10)，用▽(n)表示J(n)對W(n)求導后的梯度，表示為：

(13)

當式(13)等于0時，目標函數J(n)取得最小值，此時最佳權矢量W0為：

W0=Q-1P

(14)

采用最速下降法獲得權系數的遞推公式。按照這種方法，下一刻的權矢量W(n+1)等于當前的權矢量W(n)減去一個正比于梯度▽(n)的變化量，即：

W(n+1)=W(n)-μ▽(n)

(15)

式中，μ為收斂系數或收斂因子。

在實際應用中，為便于系統的實時實現，取單個誤差樣本的平方的梯度作為均方誤差梯度的估計，即：

(16)

將式(11)代入式(10)，推導出迭代表達式為：

W(n+1)=W(n)+2μe(n)X(n)

(17)

1.2.2算法性能分析

由于LMS算法的權系數、迭代速度等受收斂系數的值影響，因此，μ的取值很關鍵。

式(17)可改寫為：

W(n+1)=W(n)+2μX(n)[d(n)-XT(n)W(n)]=

W(n)+2μP-2μQW(n) =

[I-2μQ]W(n)+2μQW0

(18)

E[W(n+1)-W0]=[I-2μQ]E[W(n)-W0]

(19)

式中，Q為正定矩陣，可用對角矩陣表示為：

Q=AT∧A=A-1∧A

(20)

將V(n)代入式(19)，得到：

V(n)=W(n)-W0

(21)

E[V(n+1)]=A-1[I-2μ∧]AE[V(n)]

(22)

將矢量V(n)的初始值設為V(0),得到：

E[V(n)]=A-1[I-2μ∧]nAE[V(0)]

(23)

式(23)的收斂條件為：

|1-2μλmax|<1

(24)

式中λmax為最大特征值，算法穩定條件為：

(25)

通常，用正定矩陣Q的跡表示收斂條件：

(26)

收斂因子μ過小會降低系統的收斂速度，過大會產生大的權矢量噪聲，進而導致失調量增大。因此，選擇合適的μ值可以保證系統穩定。進一步地，通過分析發現收斂速度是影響LMS算法性能的一個重要因素。

2 基于卷積神經網絡的路面圖像識別

2.1 VGG16神經網絡

VGG16是一種簡潔且高效的神經網絡結構[8-11]，如圖2所示。相比于AlexNet[12-14],VGG16采用幾個小的卷積核(例如3*3卷積核)替代AlexNet中較大的卷積核(例如5*5和7*7的卷積核)提高神經網絡的訓練效果。

圖2 VGG16網絡結構示意圖

VGG16中，卷積層用于提取圖像特征。式(27)～(29)表示卷積層的特征提取過程。式中：a(l)是第l層的中間結果；a(l)是l層經過激活函數處理后的值。l+1層中包含用作l+1層輸入a(l)的第l層的輸出，權重W(l)、偏置b(l)、激活函數f、中間結果z(l+1)和輸出a(l+1)。一般情況下，卷積層需要使用激活函數來獲得非線性表示，因為非線性表示相比線性表示具有更強的表達效果。激活函數是relu激活函數，如式(30)所示。卷積層的輸入/輸出數據稱為特征圖，卷積層進行卷積運算，卷積運算相當于圖像處理中的“濾波器運算”。

z(l)=W(l)+b(l)

(27)

?

z(l+1)=W(l)a(l)+b(l)

(28)

a(y)(l+1)=f(z(l+1))

(29)

(30)

池化層是縮小長、高方向上的空間運算，能夠縮小空間大小，分為最大池化和平均池化。

全連接層把通過卷積層和池化層獲得的特征結果映射到樣本的標記空間，得到分類結果并輸出。使用softmax分類器實現分類，softmax定義為

(31)

其中：S表示樣本x是某一類的概率；ai表示分類器前一級的輸出；C表示類別的數量。softmax將多分類輸出轉換為概率。

2.2 VGG16遷移學習模型

運用遷移學習的方法可將從其他領域學到的知識應用到所需的研究領域。比如，在訓練神經網絡的過程時，需要大量的樣本對模型進行訓練和優化。但是，即使有足夠的樣本，處理樣本數據也是一個復雜的過程。遷移學習法可以彌補數據不足或訓練時間不足、時間過長造成的問題。

VGG16卷積神經網絡具有深層網絡結構，可以提取和精煉圖形中的特征。在開始時，卷積層只提取圖像特征，在網絡層較深時才處理特定任務。因此，在遷移學習[15]過程中，可將預處理過的模型應用于源域，保留下層的權值，只訓練上層，并微調相關參數。根據不同特征的源域數據分布，利用目標域數據集微調模型，去掉原有的頂層，增加新的輸出層，并增加softmax函數分類新問題。圖3顯示了卷積神經網絡模型的遷移過程。通過對源域(自然圖像)的訓練權值進行遷移，對目標域(任務數據)進行微調，極大簡化了模型在新域問題中的訓練過程。

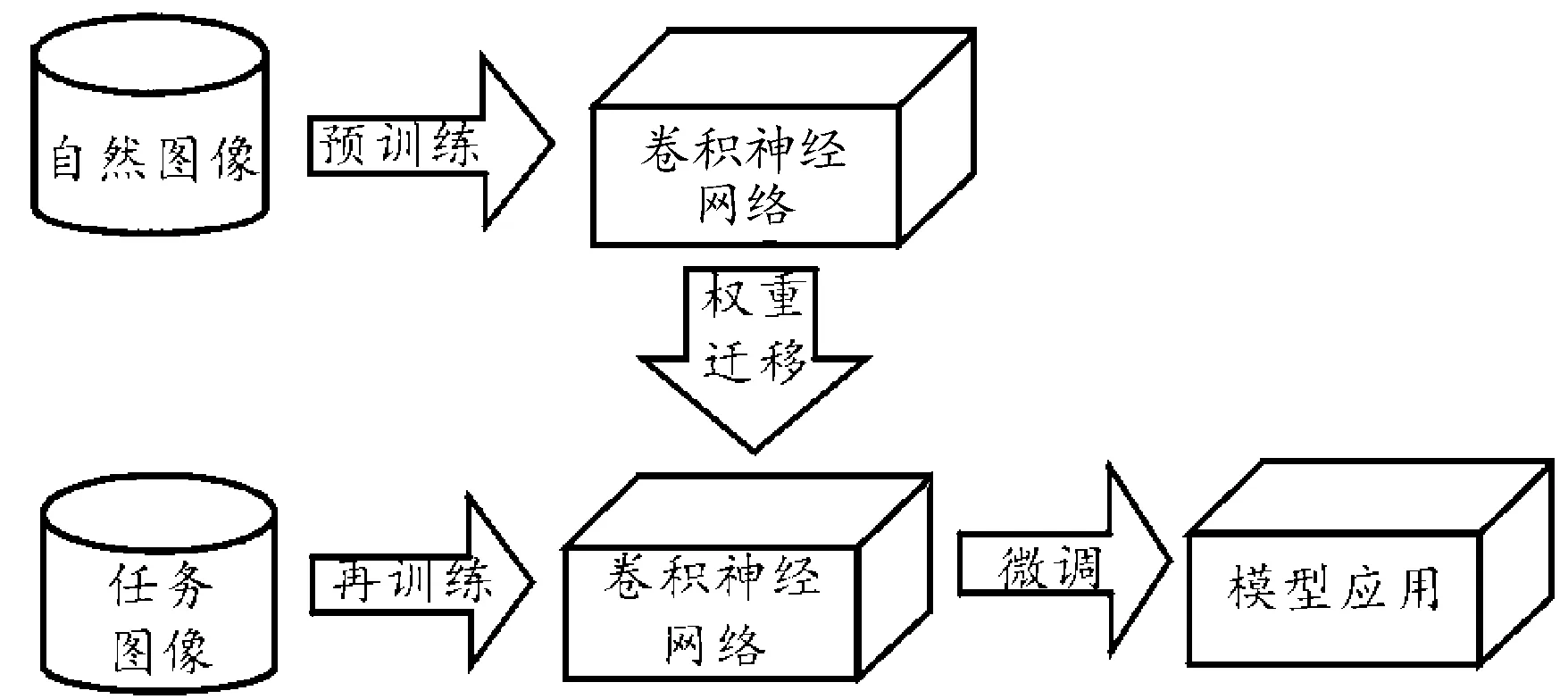
圖3 卷積神經網絡模型遷移過程示意圖

2.3 數據集制作過程

1) 圖片采集：使用攝像頭采集路面圖片，攝像頭為單目變焦攝像頭(如圖4所示)。采集的路面圖片可以分為3類，即3種不同粗糙度的路面。

圖4 單目攝像頭實物圖片

2) 對采集到的3種不同類型的路面圖片進行篩選，留下有用圖片，并對篩選后的圖片進行裁剪，得到所需圖片中的主體部分；再對圖片進行排序編號，放入分類好的文件夾中。

2.4 數據預處理與增強

首先將采集的路面圖片按照粗糙程度不同分為3類，剔除模糊不清的數據。剔除后的數據樣本總量為1 000張圖片，按照7∶2∶1的比例，把所有有用圖像分為訓練集、驗證集和測試集。隨之進行數據增強與擴充，將路面圖像隨機旋轉30°，水平方向和垂直方向隨機平移30%。對圖像進行隨機水平翻轉，并將圖像隨機縮放的幅度設置為0.5。最后，將所有路面圖像調整為224×224像素，對作為輸入層的圖像進行批量歸一化(batch normalization,BN)處理。BN處理不僅可以有效緩解梯度消失問題，還可以增強網絡的泛化能力和收斂速度。

3 模型訓練與結果分析

3.1 模型訓練

實驗硬件環境：CPU為 Intel(R)Core(TM)i5-10300H CPU @2.50GHz；GPU為NVIDIA GeForce RTX 2070；深度學習框架為VGG16。

把采集的路面圖像放入VGG16網絡模型中進行訓練，模型的優化算法采用隨機梯度下降(stochastic gradient descent,SGD)算法。設SGD優化器初始學習率為0.000 1，最小批量值(mini-batch size)設置為10，驗證頻率(validation frequency)設置為3。模型訓練的損失函數是交叉熵損失函數，最后將epoch值設置為200開始進行訓練。

3.2 結果分析

分析圖5的訓練集與驗證集的準確率、損失率曲線可知，在經過約50次迭代后，模型趨近收斂，且曲線的趨勢基本重合。準確率曲線在數值上接近1，損失率曲線接近于0。訓練結束后，通過編寫代碼，從路面圖片的驗證集中隨機抽取6個圖片導入訓練好的網絡模型中。從6個路面圖片中選取3張不同路面類型的圖片，識別效果見圖6，每個路面圖片上方顯示了驗證結果和準確率。可以發現，通過攝像頭采集的3種路面，完成訓練的CNN具有良好的識別效果和泛化能力。

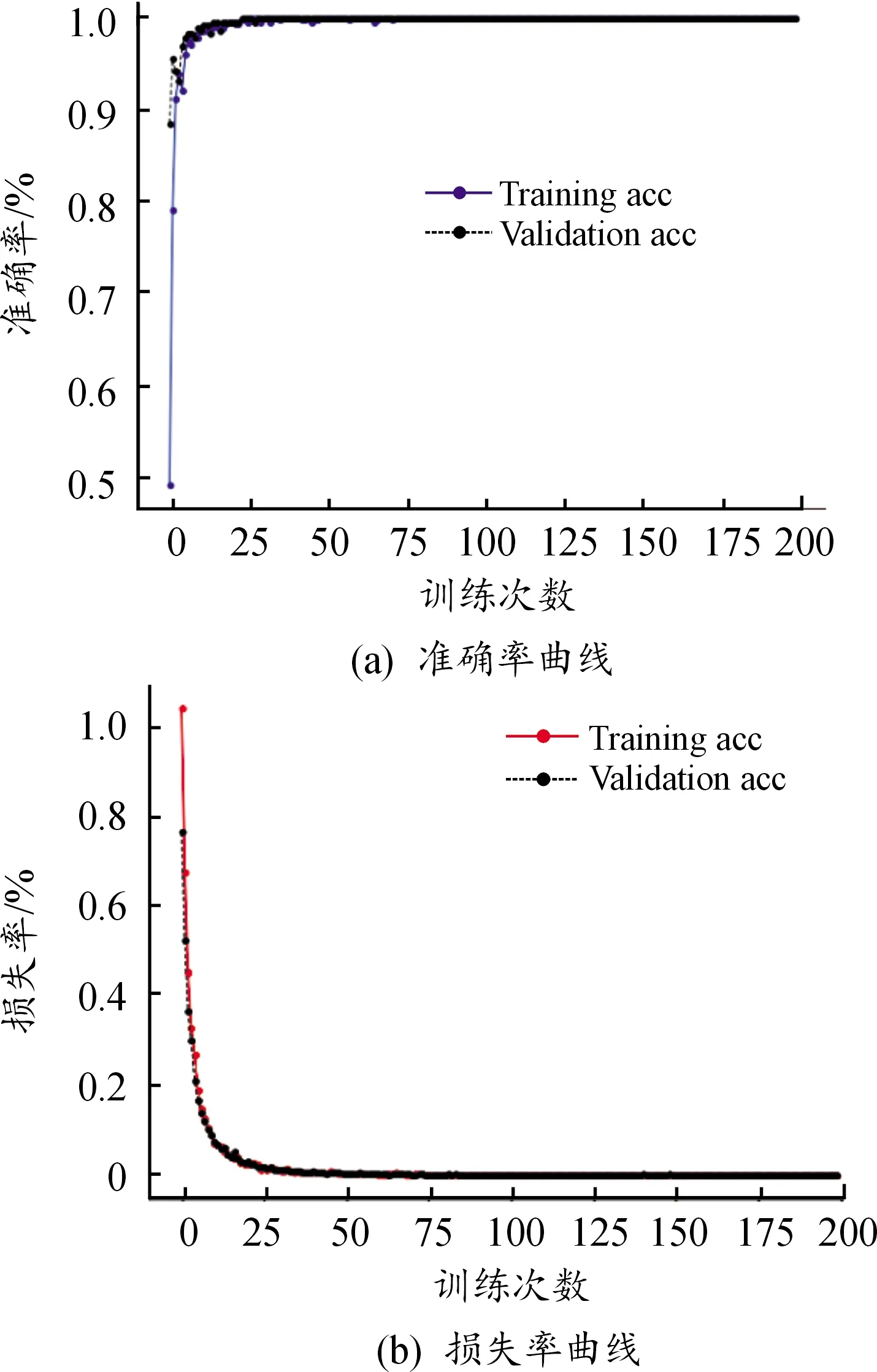
圖5 VGG16訓練和驗證結果曲線

圖6 驗證結果和準確率場景圖

4 仿真分析

4.1 路噪主動控制流程

路面識別和路噪主動控制的過程(見圖7)由路面圖像采集、路面類型識別和路噪主動控制3部分組成。從圖7可以看出:首先，路面圖像由攝像頭采集，作為CNN的輸入；其次，CNN通過預訓練識別輸入圖像；最后，根據識別結果選擇相應路面下路噪主動控制系統的收斂因子，實現車輛在不同道路下的調整，達到減小車輛路面噪聲的目的。對3種不同類型路面進行仿真分析，比較3種路面的原始噪聲和3種路面收斂因子取中間值以及根據不同類型路面調整收斂因子后的降噪效果。

圖7 基于路面識別的路噪主動控制流程框圖

4.2 3種路面仿真結果

為保證車輛在不同類型的路面行駛時具有良好的舒適性，需對路噪主動控制系統調整收斂因子，找到各個路面對應的最優收斂因子，使其在不同路面類型下達到最優的降噪效果。根據所建立的路噪主動控制模型，以LMS算法收斂因子為優化變量，以路面噪聲為優化目標。根據LMS算法的收斂特性，不同工況條件下最優收斂因子不同，故針對不同路面，使用不同收斂因子進行大量仿真，通過觀測控制效果預標定本系統在3種不同路面工況下的最優收斂因子值。針對不同的路面激勵，經過前期大量的篩選，選出接近最優降噪效果的3種收斂因子，比較分析得出最優收斂因子，獲得當前路面噪聲的最優降噪效果。以某車型在不同路面采集的原始噪聲作為參照，得到仿真結果如圖8所示。

圖8 不同路面類型時各收斂因子降噪效果曲線

在建立的仿真模型中，采樣時間設定為30 s，采樣頻率設定為2 000 Hz，控制濾波器選用常用的有限脈沖響應FIR濾波器；模型輸入為60 km/h下采集的不同路面噪聲信號，模型輸出為頭枕處揚聲器發出的次級信號。由圖8得到各路面降噪效果如下：

1) 在60 km/h的瀝青路面,80～550 Hz頻帶范圍內，當收斂因子取31時的平均降噪量為2.5 dB，頻率為230 Hz處的峰值降噪量為6.4 dB；當收斂因子取29時，平均降噪量為3.7 dB，在頻率230 Hz處的峰值降噪量為13.2 dB；當收斂因子取30時，平均降噪量為4.3 dB，在頻率230 Hz處的峰值降噪量可以達到16.3dB。

2) 在60 km/h的泥土路面下，80～550 Hz頻帶范圍內，當收斂因子取9時的平均降噪量為4.6 dB，頻率225Hz處的峰值降噪量為11.5 dB；當收斂因子為11時，平均降噪量為4.15 dB，頻率225 Hz處的峰值降噪量為10.4 dB；當收斂因子取10時，平均降噪量為5.1 dB，頻率225 Hz處的峰值降噪量可以達到13.5 dB。

3) 在60 km/h的鋸齒形路面下，80～550 Hz頻帶范圍內，當收斂因子取1時的平均降噪量為3.3 dB，頻率228 Hz處的峰值降噪量為10.9 dB；當收斂因子為3時，平均降噪量為3.7 dB,頻率228 Hz處的峰值降噪量為12 dB；當收斂因子調整為2時，平均降噪量為4.3 dB，頻率228 Hz處的峰值降噪量可以達到14.7 dB。

將上述3組降噪數據匯總得到表1，經分析發現：當車輛行駛在瀝青路面時，調整收斂因子為30，取得的降噪效果最好；當車輛行駛在泥土路面時，調整收斂因子為10，降噪效果最好；當車輛行駛在鋸齒路面時，調整收斂因子為2，取得的降噪效果最好。

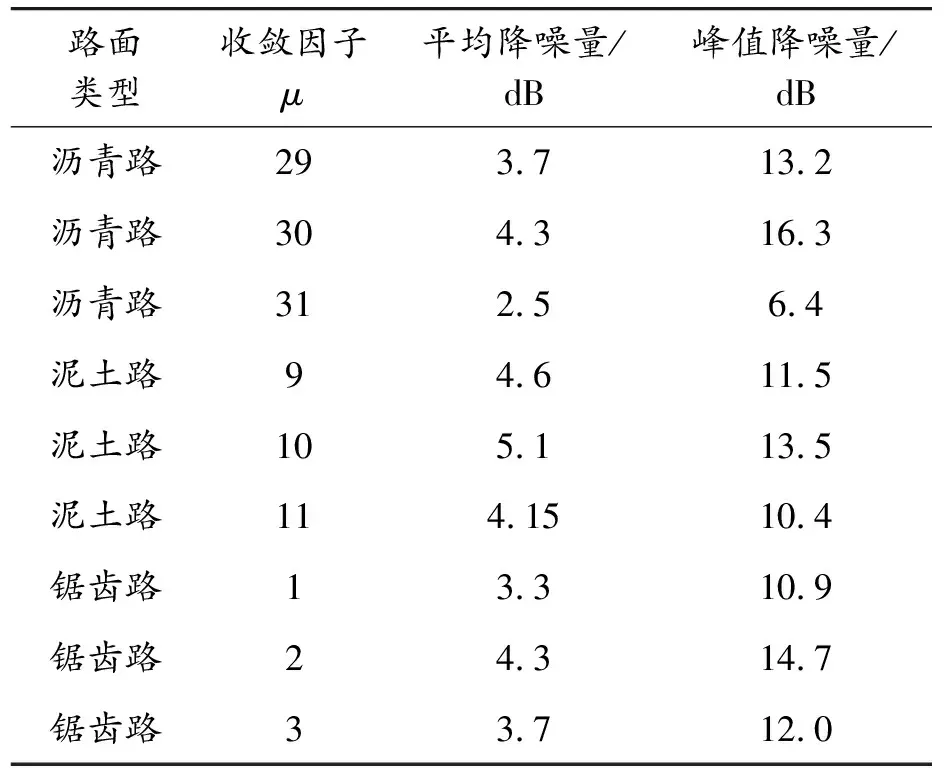
表1 各種路面類型時不同收斂因子的降噪量

對比表1中的平均降噪量數據，得到不同路面類型下的最優收斂因子。在已建立的仿真模型中加入路面預判，以路面圖片作為輸入，在已訓練好的卷積神經網絡中進行分類，從而識別路面類型，對應該路面下的最優收斂因子，獲得降噪效果。取3種路面最優收斂因子的中間值，以獲得3種路面取同一收斂因子時的降噪效果。統一與路面無控制的原始噪聲進行對比，得到仿真結果(見圖9)。

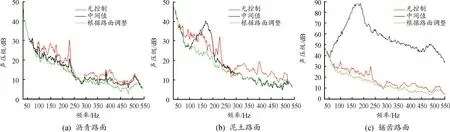
圖9 不同路面類型下優化前后降噪效果曲線

分析表2中各路面類型優化前后的降噪量可發現：當路噪主動控制系統在不同路面類型下只選取相同的1個收斂因子時，不能保證在所有路面類型下都取得最好的降噪效果。即在不同路面類型下取1個相同的收斂因子時，其降噪效果低于預判路面類型，故不同路面下應選取該路面對應的最優收斂因子，以獲得最佳效果。

表2 各路面優化前后降噪量

5 結論

1) 在模型訓練過程中，可通過數據批量歸一化和數據增強兩種措施來增強網絡的收斂速度和泛化能力。

2) 運用卷積神經網絡的路面識別方法可以準確識別采集到的3種不同類型路面。

3) 基于路面識別的路噪主動控制系統可根據不同路面類型調整收斂因子，提升車輛在不同路面的噪聲優化效果。