考慮最大制動(dòng)能量回收功率的再生制動(dòng)模糊控制
何 仁,朱思宇
(江蘇大學(xué) 汽車與交通工程學(xué)院, 江蘇 鎮(zhèn)江 212013)
再生制動(dòng)能夠在車輛減速制動(dòng)時(shí)回收車輛的部分動(dòng)能,并能將其儲(chǔ)存起來(lái)用以驅(qū)動(dòng)車輛,提高電動(dòng)車輛的續(xù)航里程[1]。近年來(lái),輪轂電機(jī)由于控制精度高,響應(yīng)快,更容易集成多種節(jié)能新技術(shù)[2],同時(shí)輪轂電機(jī)驅(qū)動(dòng)車輛省去了機(jī)械傳動(dòng)部分,能夠有效地提高制動(dòng)能量回收效率[3],所以輪轂電機(jī)驅(qū)動(dòng)車輛的再生制動(dòng)技術(shù)成為了當(dāng)前新能源汽車領(lǐng)域的研究熱點(diǎn)之一。
如何在保證制動(dòng)安全的前提下合理分配輪轂電機(jī)驅(qū)動(dòng)車輛的再生制動(dòng)力矩與液壓制動(dòng)力矩,盡可能多地回收制動(dòng)能量,一直是亟待解決的關(guān)鍵問(wèn)題之一[4]。再生制動(dòng)系統(tǒng)被認(rèn)為是一種具有非線性參數(shù)和嚴(yán)重干擾的不確定性系統(tǒng),而模糊控制因其具有較強(qiáng)的魯棒性[5],適用于非線性系統(tǒng)的控制,所以在再生制動(dòng)控制中得到了廣泛應(yīng)用。國(guó)內(nèi)外關(guān)于再生制動(dòng)模糊控制策略具有較多的成果:Zhang等[6]利用模糊控制策略對(duì)混合動(dòng)力車輛的再生制動(dòng)力矩和液壓制動(dòng)力矩進(jìn)行分配;Cao等[7]采用田口優(yōu)化方法對(duì)模糊控制策略隸屬函數(shù)進(jìn)行優(yōu)化,優(yōu)化后的控制策略能有效地回收更多的能量;陳澤宇等[8-10]提出了一種基于車速、制動(dòng)強(qiáng)度、電池的荷電狀態(tài)的模糊控制方法分配機(jī)電復(fù)合制動(dòng)力矩;Zhang等[11-12]設(shè)計(jì)了以制動(dòng)強(qiáng)度、車速和需求制動(dòng)力矩為輸入,再生制動(dòng)力矩占總制動(dòng)力矩的比值為輸出的模糊控制器。雖然上述研究成果在克服傳統(tǒng)摩擦制動(dòng)系統(tǒng)響應(yīng)時(shí)間長(zhǎng)的缺陷的同時(shí)能夠在一定程度上提高車輛能量利用效率,但是它們?cè)谠O(shè)計(jì)模糊控制規(guī)則過(guò)程中并沒(méi)有將再生制動(dòng)系統(tǒng)實(shí)時(shí)回收功率最大作為設(shè)計(jì)依據(jù),而導(dǎo)致再生制動(dòng)系統(tǒng)沒(méi)有充分發(fā)揮能量回收功能[13]。
為了進(jìn)一步挖掘再生制動(dòng)系統(tǒng)的制動(dòng)能量回收效果,本文研究了最大制動(dòng)能量回收功率與電機(jī)的充電電壓之間的關(guān)系,考慮電池荷電狀態(tài)對(duì)再生制動(dòng)影響的同時(shí),分析了最大制動(dòng)能量回收功率的特點(diǎn),并據(jù)此設(shè)計(jì)了一種以車速、制動(dòng)強(qiáng)度和最大制動(dòng)能量回收功率下的再生制動(dòng)力矩與單個(gè)車輪的制動(dòng)力矩的比值為輸入條件的三輸入一輸出的再生制動(dòng)模糊控制策略。研究結(jié)果表明:所提出的控制策略能夠有效地改善再生制動(dòng)系統(tǒng)的制動(dòng)能量回收性能。
1 分布式電驅(qū)動(dòng)車輛制動(dòng)系統(tǒng)結(jié)構(gòu)
以分布式電驅(qū)動(dòng)車輛作為研究對(duì)象。圖1為分布式電驅(qū)動(dòng)車輛總體結(jié)構(gòu)示意圖[14]。如圖1所示:4個(gè)車輪都由電機(jī)控制,車輛制動(dòng)時(shí),再生制動(dòng)系統(tǒng)采集制動(dòng)踏板位移等信號(hào)確定再生制動(dòng)力矩和液壓制動(dòng)力矩的分配比例,將其發(fā)送到整車控制器(VCU),VCU將再生制動(dòng)力矩指令發(fā)送給電機(jī)控制器(MCU),將液壓制動(dòng)力矩發(fā)送給液壓控制器。液壓控制器根據(jù)液壓制動(dòng)力矩指令計(jì)算出目標(biāo)制動(dòng)輪缸的壓力,采集輪缸壓力信號(hào)并進(jìn)行控制,MCU根據(jù)再生制動(dòng)力矩指令對(duì)電機(jī)進(jìn)行控制,輸出再生制動(dòng)力矩作用在車輪上,同時(shí)將產(chǎn)生的能量輸送到電池組。
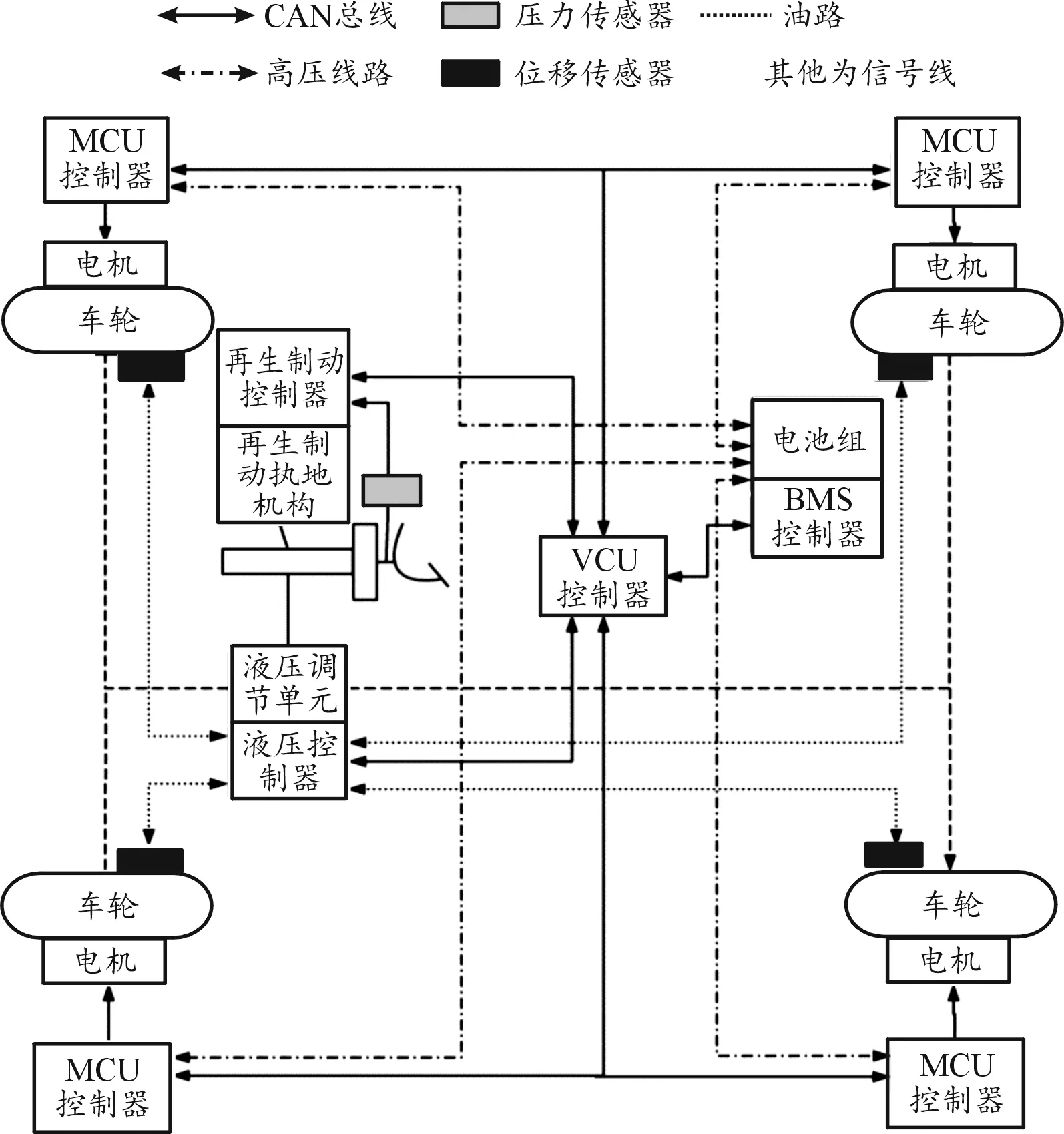
圖1 分布式電驅(qū)動(dòng)車輛總體結(jié)構(gòu)示意圖
2 數(shù)學(xué)模型
2.1 車輛縱向動(dòng)力學(xué)模型
車輛在水平路面進(jìn)行制動(dòng)時(shí),其受力情況如圖2所示。
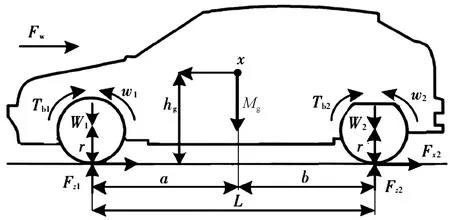
圖2 車輛制動(dòng)過(guò)程受力示意圖
對(duì)圖2進(jìn)行縱向動(dòng)力學(xué)分析,可得車輛制動(dòng)時(shí)的縱向力平衡力方程:
(1)
車輪的平衡方程:
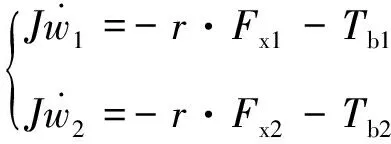
(2)
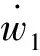
Tb1和Tb2的表達(dá)式為:
(3)
式中:Tm1、Tm2分別表示前、后輪的再生制動(dòng)力矩;Th1、Th2分別表示前、后輪的再生制動(dòng)力矩。
為了保證汽車在制動(dòng)時(shí)的制動(dòng)穩(wěn)定性,根據(jù)ECE R13制動(dòng)法規(guī)選取汽車的前后軸制動(dòng)力分配系數(shù)。ECE R13法規(guī)規(guī)定[15]:

(4)
式中:β為前后軸制動(dòng)力分配系數(shù),z為制動(dòng)強(qiáng)度,a為前軸到質(zhì)心的距離,b為后軸到質(zhì)心的距離,hg為質(zhì)心高度,L為前軸到后軸的距離。
經(jīng)過(guò)計(jì)算,車輛前后軸制動(dòng)力分配系數(shù)取值范圍為0.71~0.99,本文取前后軸制動(dòng)力分配系數(shù)0.72。
2.2 輪胎模型
本文所采用的輪胎模型是Pacejka教授提出的Magic Formula輪胎模型,通用表達(dá)式為[16]:
Fx=Dsin{Carctan[Bs-E(Bs-arctan(Bs))]}
(5)
式中:s為車輪縱向滑移率;B、C、D、E分別為魔術(shù)公式中與輪胎特性相關(guān)的參數(shù)。
前、后車輪的縱向滑移率s1、s2可由下式表示:
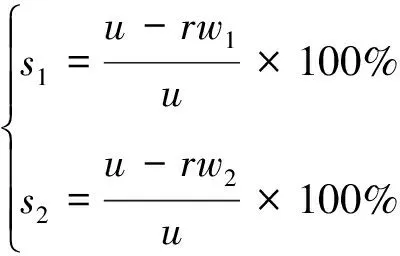
(6)
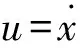
2.3 再生-液壓復(fù)合制動(dòng)系統(tǒng)模型
2.3.1再生制動(dòng)系統(tǒng)模型
本文研究的車輛采用4個(gè)相互獨(dú)立的輪轂電機(jī)進(jìn)行驅(qū)/制動(dòng),輪轂電機(jī)類型為直流無(wú)刷電機(jī),電機(jī)模型由電壓方程和扭矩方程進(jìn)行表示:
(7)
Tm=Kt·i
(8)
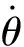
考慮到電機(jī)的非線性飽和特性和電池充電安全,設(shè)置充電電流不大于200 A。
2.3.2液壓制動(dòng)系統(tǒng)模型
由于再生制動(dòng)提供的制動(dòng)力矩有限,無(wú)法滿足車輛在大制動(dòng)工況下的制動(dòng)需求,車輛還需要裝有常規(guī)的液壓制動(dòng)系統(tǒng)。液壓制動(dòng)系統(tǒng)包括制動(dòng)主缸、高速開(kāi)關(guān)閥、制動(dòng)輪缸。制動(dòng)輪缸通過(guò)高速開(kāi)關(guān)閥與制動(dòng)主缸及低壓蓄能器連接,控制器控制高速開(kāi)關(guān)閥對(duì)制動(dòng)輪缸進(jìn)行增壓或者減壓控制,制動(dòng)輪缸壓力可由下式表示[17]:
(9)
式中:Pm為主缸壓力;Pr為低壓蓄能器的壓力;Pw為輪缸壓力;τ和τ′分別為電磁閥和管路傳輸?shù)臏髸r(shí)間;u1和u2分別為電磁閥控制的指令信號(hào)。常用一階慣性環(huán)節(jié)來(lái)表征液壓制動(dòng)系統(tǒng)的時(shí)間滯后,即:
(10)
式中:Th(s)和Pw(s)分別為實(shí)際液壓制動(dòng)力矩和目標(biāo)液壓制動(dòng)力矩;Kb為制動(dòng)力矩常數(shù);σ為反映制動(dòng)器動(dòng)態(tài)特性常數(shù)。
2.4 電池荷電狀態(tài)估算模型
用電池荷電狀態(tài)SOC來(lái)表示電池剩余電量的百分比,SOC為電池剩余電量和電池總電量的比值,可由下式計(jì)算可得:
(11)
式中:Ecap為電池總電量,Eres為電池剩余電量,Euse為電池使用過(guò)的電量,SOC=0表示電池電量已經(jīng)耗盡,SOC=1表示電池滿電量狀態(tài)。
3 復(fù)合制動(dòng)控制策略
3.1 再生制動(dòng)能量回收功率分析
現(xiàn)有的模糊控制策略由于沒(méi)有考慮再生制動(dòng)能量回收功率這一因素,在實(shí)際再生制動(dòng)控制過(guò)程中導(dǎo)致制動(dòng)能量回收效率偏低。為了實(shí)現(xiàn)電動(dòng)車輛再生-液壓復(fù)合制動(dòng)控制過(guò)程中制動(dòng)能量回收功率最大化,本文旨在通過(guò)研究再生制動(dòng)能量回收功率的特點(diǎn),調(diào)節(jié)再生制動(dòng)力矩占總制動(dòng)力矩的比值q,從而達(dá)到提高制動(dòng)能量回收效率的目的。
再生制動(dòng)能量回收功率取決于制動(dòng)過(guò)程中電機(jī)的充電電壓和充電電流。制動(dòng)能量回收功率P可由下式表示:
P=Ui
(12)
電機(jī)的充電電壓由式(7)給出,由于L較小,可忽略不計(jì)。式(7)可以近似等效于下式
(13)
將式(13)代入式(12),則有:
(14)
制動(dòng)能量回收功率對(duì)時(shí)間的積分可得再生制動(dòng)回收能量E,可由下式表示:

(15)
式中:T為制動(dòng)總時(shí)間。
將式(14)代入式(15)可得:
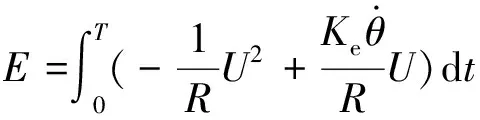
(16)
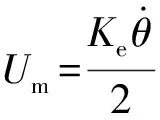
(17)
(18)
結(jié)合式(17)(18)可得:
(19)
由上述分析可知,通過(guò)調(diào)節(jié)電機(jī)的充電電壓可以使電機(jī)工作在最大再生制動(dòng)能量回收功率狀態(tài)。
又電機(jī)的轉(zhuǎn)速可由下式表示:
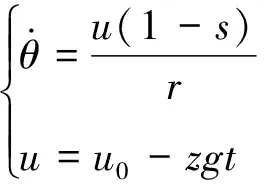
(20)
式中:u0為制動(dòng)初速度。
將式(20)代入(19)可得:
(21)
因此,再生制動(dòng)回收能量可由下式表示:
(22)
式中:T為制動(dòng)總時(shí)間。
當(dāng)車輛型號(hào)和電機(jī)選定后,Ke、R、r是常量,在常規(guī)制動(dòng)工況下,車輛處于穩(wěn)態(tài)時(shí),滑移率近似保持不變,因此可設(shè)一個(gè)常數(shù)k,令
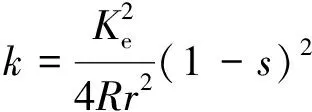
(23)
式(22)等效為:
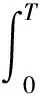
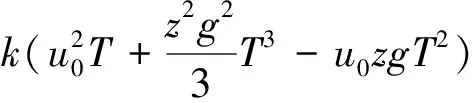
(24)
當(dāng)車輛由初速度u0按制動(dòng)強(qiáng)度z完成制動(dòng)時(shí),可得:
0=u0-zgT
(25)
(26)
將式(26)代入式(24),可得:
(27)
式(27)可簡(jiǎn)化為:
(28)
通過(guò)對(duì)制動(dòng)能量回收功率的分析,推導(dǎo)出再生制動(dòng)能量回收的公式。由式(28)可知:最大制動(dòng)能量回收功率下的再生制動(dòng)回收的能量還與車輛初始速度和制動(dòng)強(qiáng)度有關(guān),因此,在設(shè)計(jì)再生制動(dòng)控制策略時(shí),需要考慮車輛初始速度和制動(dòng)強(qiáng)度對(duì)制動(dòng)能量回收的影響。
3.2 再生制動(dòng)模糊控制策略設(shè)計(jì)
傳統(tǒng)的電動(dòng)車輛再生制動(dòng)模糊控制策略,以車速u、制動(dòng)強(qiáng)度z和電池SOC作為模糊控制的輸入,再生制動(dòng)力矩占總制動(dòng)力矩的比值q作為模糊控制的輸出[18],液壓制動(dòng)力矩作為補(bǔ)償力矩。但是,在模糊控制策略中并沒(méi)有考慮到最大再生制動(dòng)能量回收功率這一因素。
本文在傳統(tǒng)的模糊控制策略基礎(chǔ)上,仍將車速、制動(dòng)強(qiáng)度作為所設(shè)計(jì)的模糊控制策略的輸入,同時(shí)為了盡可能獲得再生制動(dòng)過(guò)程中最大制動(dòng)能量回收功率,設(shè)計(jì)了一個(gè)新的模糊控制輸入K,K滿足:
K=Tm_Pmax/Tb
(29)
K的論域設(shè)定為[0,1],當(dāng)K趨于1時(shí),即最大制動(dòng)能量回收功率情況下的再生制動(dòng)力矩基本滿足車輪所需的制動(dòng)力矩,此時(shí)再生制動(dòng)力矩占總制動(dòng)力矩的比值q應(yīng)大一些,即Tb·q的值接近Tm_Pmax,此時(shí)制動(dòng)能量回收也更多;當(dāng)K趨于0時(shí),即最大制動(dòng)能量回收功率情況下的再生制動(dòng)力矩占車輪制動(dòng)力矩的比值很小,此時(shí)再生制動(dòng)力矩占總制動(dòng)力矩的比值q應(yīng)小一些。
控制器的輸入變量車速u的模糊子集有[S,M,B],論域?yàn)閇0,30];制動(dòng)強(qiáng)度z的模糊子集為[S,M,B],論域?yàn)閇0,1];K的模糊子集為[S,M,B],論域?yàn)閇0,1];輸出變量q的模糊子集為[S,M,B],論域?yàn)閇0,1]。其中S表示小,M表示中,B表示大。
根據(jù)理論分析,所設(shè)計(jì)的控制策略中,車速、制動(dòng)強(qiáng)度、最大制動(dòng)能量回收功率下的再生制動(dòng)力矩占單輪理想總制動(dòng)力矩的比值與實(shí)際再生制動(dòng)力矩占比的三維圖,如圖3所示。
模糊控制規(guī)則如表1所示。
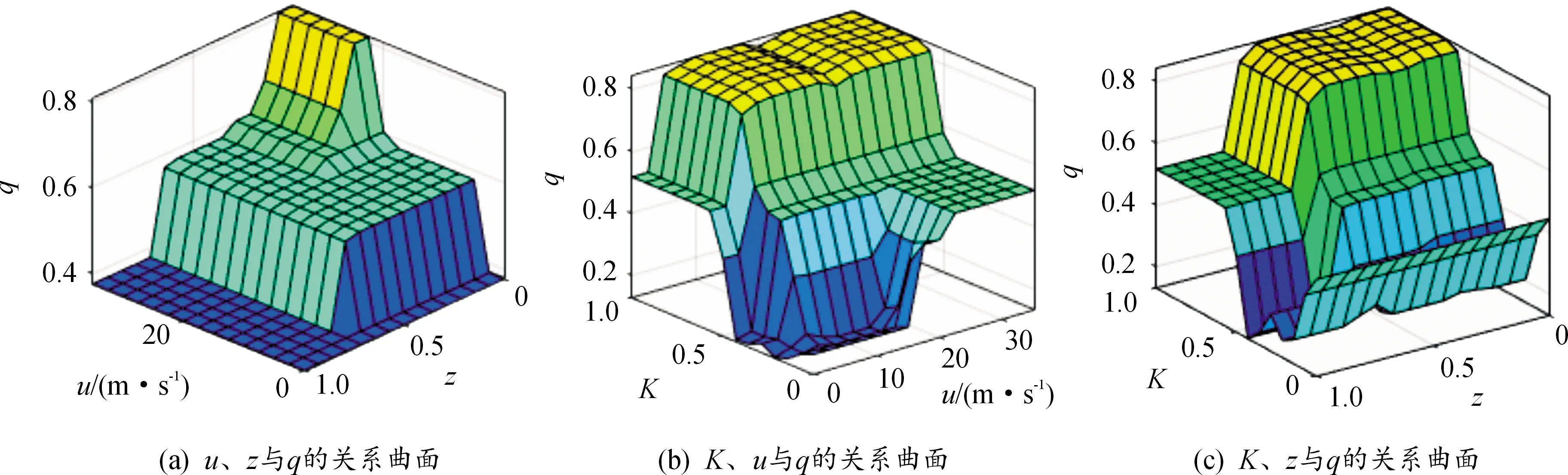
圖3 模糊控制三維示意圖
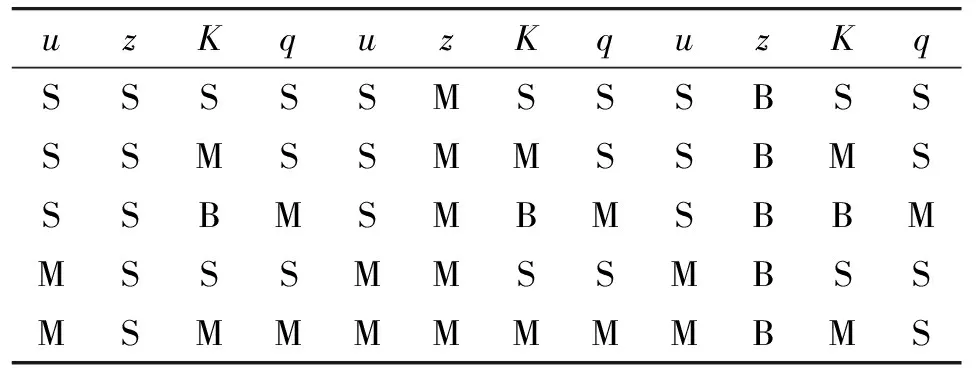
表1 模糊控制規(guī)則
uzKquzKquzKqMSBBMMBBMBBMBSSMBMSMBBSMBSMHBMMMBBMSBSBHBMBHBBBM
考慮到電池SOC對(duì)再生制動(dòng)力矩的影響,引入電池荷電狀態(tài)系數(shù)Ksoc對(duì)再生制動(dòng)力矩進(jìn)行修正,Ksoc由下式表示:
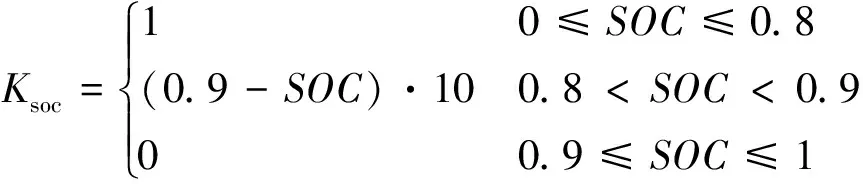
(30)
根據(jù)所提的控制策略,復(fù)合制動(dòng)系統(tǒng)的再生制動(dòng)力矩Tmi滿足:
Tmi=Tb·q·Ksoc
(31)
本節(jié)設(shè)計(jì)了以車速、制動(dòng)強(qiáng)度和最大制動(dòng)能量回收功率下的再生制動(dòng)力矩與總制動(dòng)力矩的比值為輸入,再生制動(dòng)力矩占總制動(dòng)力矩的比值為輸出的模糊控制策略,同時(shí)考慮了電池SOC對(duì)再生力矩的影響。
4 仿真分析
4.1 仿真參數(shù)
本文以分布式驅(qū)動(dòng)車輛作為研究對(duì)象,采用的部分仿真參數(shù)[19]如表2所示。
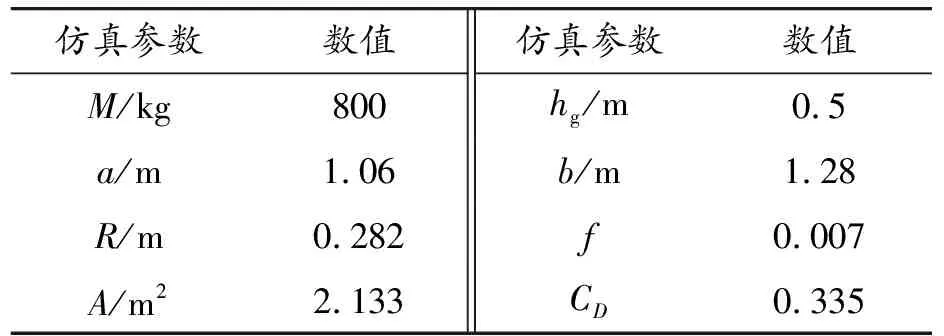
表2 仿真參數(shù)
4.2 再生制動(dòng)模糊控制策略仿真
在Matlab/Simulink環(huán)境下,根據(jù)所建立的仿真模型,設(shè)置車輛在高附著路面,以初速度20 m/s,分別在輕度制動(dòng)工況,制動(dòng)強(qiáng)度約為0.2(制動(dòng)工況1)和中度制動(dòng)工況,制動(dòng)強(qiáng)度約為0.5(制動(dòng)工況2)下進(jìn)行制動(dòng),對(duì)控制策略1(本文提出的再生制動(dòng)模糊控制策略)和控制策略2(傳統(tǒng)的再生制動(dòng)模糊控制策略)進(jìn)行了仿真對(duì)比。
4.2.1制動(dòng)工況1
圖4表示控制策略1與控制策略2的再生制動(dòng)力矩、液壓制動(dòng)力矩和總制動(dòng)力矩隨時(shí)間的變化曲線;圖5表示電機(jī)充電電壓的變化曲線;圖6表示控制策略1與控制策略2的制動(dòng)能量回收性能隨時(shí)間的變化曲線。
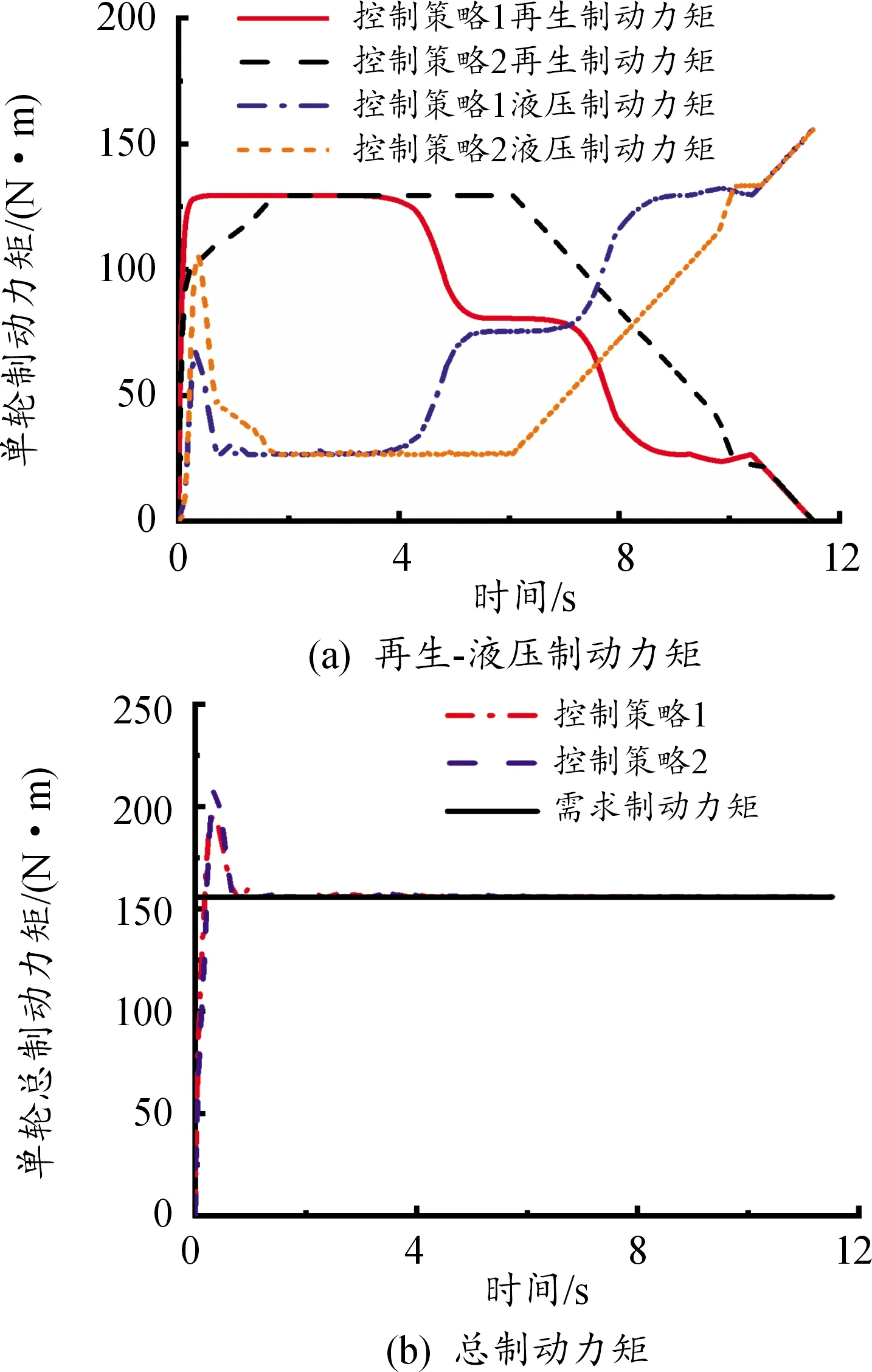
圖4 制動(dòng)工況1下的制動(dòng)力矩隨時(shí)間變化曲線
如圖4所示,控制策略1和控制策略2的再生制動(dòng)力矩與液壓制動(dòng)力矩在協(xié)調(diào)制動(dòng)過(guò)程中,能夠滿足車輛總制動(dòng)力矩的需求,且控制策略1的再生制動(dòng)力矩和液壓制動(dòng)力矩的變化較控制策略2平滑,總制動(dòng)力矩的超調(diào)量更小。
圖5為2種控制策略下的電機(jī)的充電電壓與最大制動(dòng)能量回收功率下的電機(jī)充電電壓的關(guān)系曲線。由式(14)可得,制動(dòng)能量回收功率是有關(guān)充電電壓的一元二次函數(shù),圖中Um為再生制動(dòng)系統(tǒng)最大能量回收功率時(shí)的電機(jī)充電電壓,當(dāng)實(shí)際再生制動(dòng)系統(tǒng)的電機(jī)的充電電壓越接近Um時(shí),制動(dòng)能量回收功率越大。

圖5 制動(dòng)工況1下的電機(jī)的充電電壓的變化曲線
由圖6可知,控制策略1與控制策略2在仿真前4 s內(nèi),充電電壓相近,在4 s后,控制策略1的充電電壓較控制策略2的充電電壓更接近Um,因此控制策略1的制動(dòng)能量回收功率越大。控制策略2在6 s左右時(shí),電機(jī)的充電電壓已降至0。
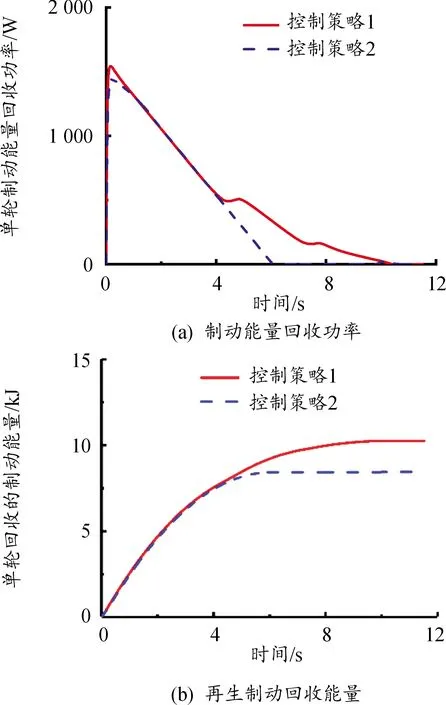
圖6 制動(dòng)工況1下的制動(dòng)能量回收性能隨時(shí)間的變化曲線
造成這一問(wèn)題的原因主要是控制策略2中再生制動(dòng)力矩所占比值較大,如圖6(a)所示,控制策略的再生制動(dòng)力矩在4 s后幾乎一直是高于控制策略1的,由電機(jī)模型的電壓方程和扭矩方程可以得到,再生制動(dòng)力矩Tm可由下式表示:
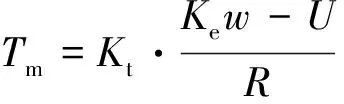
(32)
為了滿足控制策略2中的再生制動(dòng)力矩需求,充電電壓下降很快。
如圖5、6中所示,在制動(dòng)前4 s,控制策略1與控制策略2的電機(jī)充電電壓變化基本相同,制動(dòng)能量回收功率與再生制動(dòng)回收能量基本相等,4 s后,控制策略1的制動(dòng)能量回收功率與再生制動(dòng)回收能量比控制策略2高。
2種控制策略下的車輛制動(dòng)時(shí)間和制動(dòng)距離如表3所示。
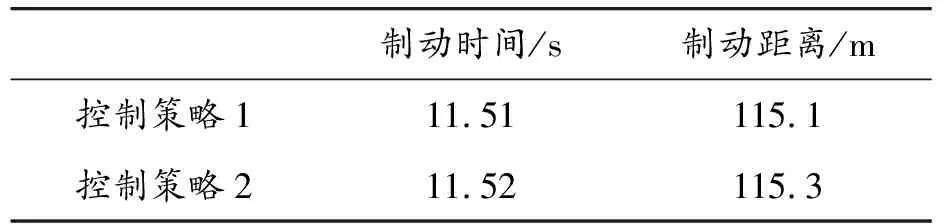
表3 制動(dòng)工況1下的2種控制策略的汽車制動(dòng)性能
由于再生制動(dòng)響應(yīng)速度較摩擦制動(dòng)快,當(dāng)總制動(dòng)力矩中再生制動(dòng)所占比例越高,其制動(dòng)響應(yīng)越快。由表3可知,采用控制策略1時(shí),汽車制動(dòng)時(shí)間和制動(dòng)距離較短,這是由于制動(dòng)初始時(shí),控制策略1中的再生制動(dòng)力矩占總制動(dòng)力矩比值較大,使總制動(dòng)力矩響應(yīng)速度相較于控制策略2更快,進(jìn)而縮短了制動(dòng)響應(yīng)時(shí)間,減少了制動(dòng)距離。
4.2.2制動(dòng)工況2
圖7表示控制策略1與控制策略2的再生制動(dòng)力矩、液壓制動(dòng)力矩和總制動(dòng)力矩隨時(shí)間的變化曲線;圖8表示電機(jī)充電電壓的變化曲線;圖9表示控制策略1與控制策略2的制動(dòng)能量回收性能隨時(shí)間的變化曲線。
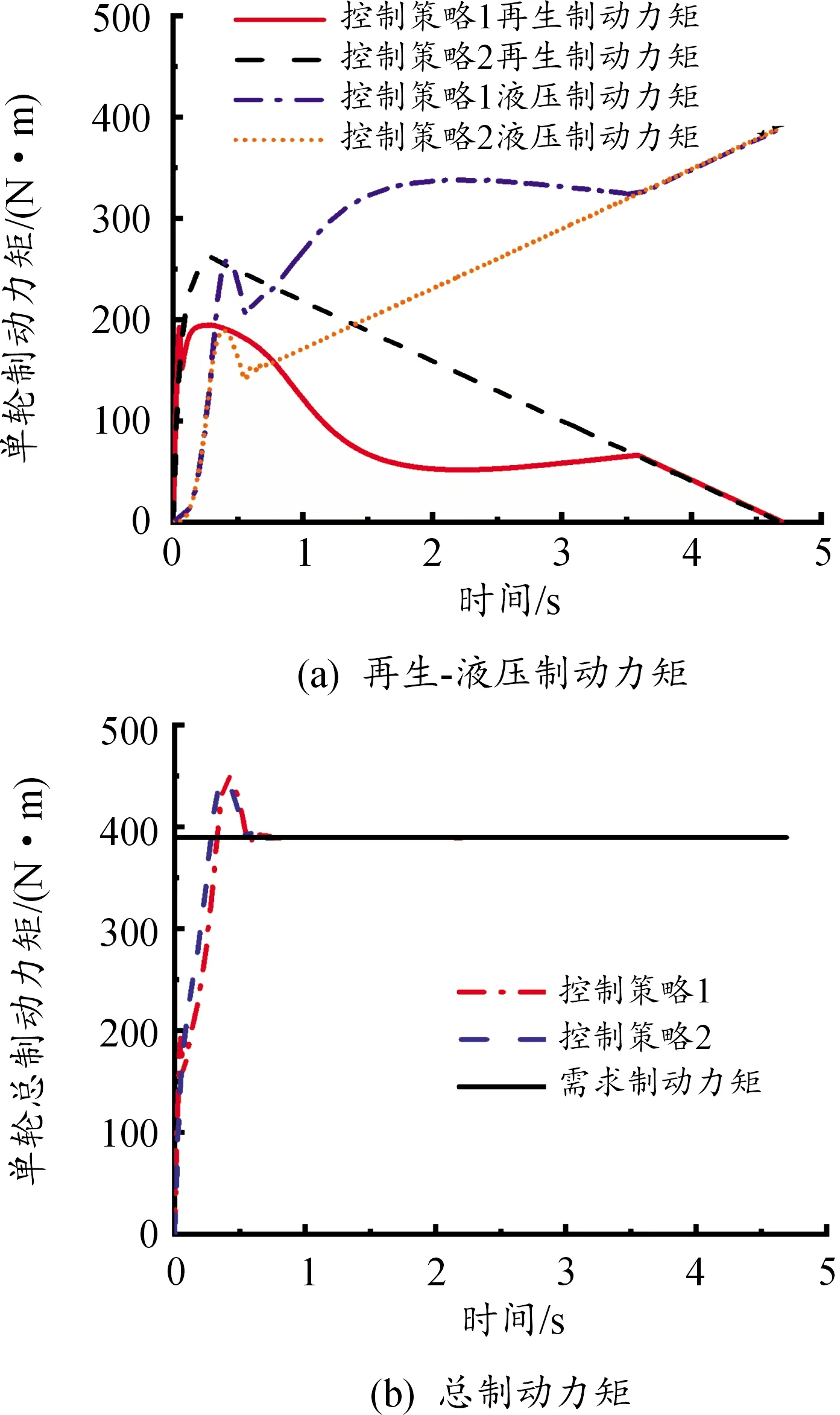
圖7 制動(dòng)工況2下的制動(dòng)力矩隨時(shí)間變化曲線
如圖7所示,控制策略1和控制策略2的再生制動(dòng)力矩與液壓制動(dòng)力矩在協(xié)調(diào)制動(dòng)過(guò)程中,能夠滿足總制動(dòng)力矩的需求。
圖8為2種控制策略下的電機(jī)的充電電壓與最大制動(dòng)能量回收功率下的電機(jī)充電電壓的關(guān)系曲線。控制策略2中,為了滿足再生制動(dòng)力矩的需求,電機(jī)的充電電壓在很短的時(shí)間內(nèi)已降為0,控制策略1的充電電壓能夠保持在Um附近,因此制動(dòng)能量回收情況如圖9所示,控制策略2的制動(dòng)能量回收功率很快降為0,不再回收制動(dòng)能量,而控制策略1能夠調(diào)整電機(jī)的充電電壓在Um附近,制動(dòng)能量回收功率和回收的制動(dòng)能量高于控制策略2。
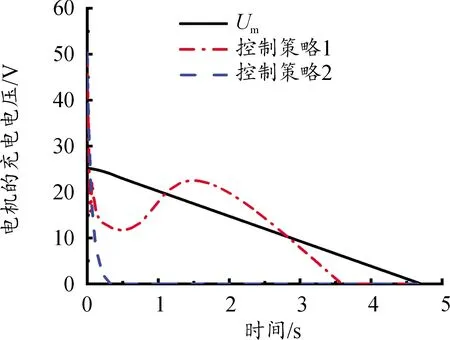
圖8 制動(dòng)工況2下的電機(jī)的充電電壓的變化曲線
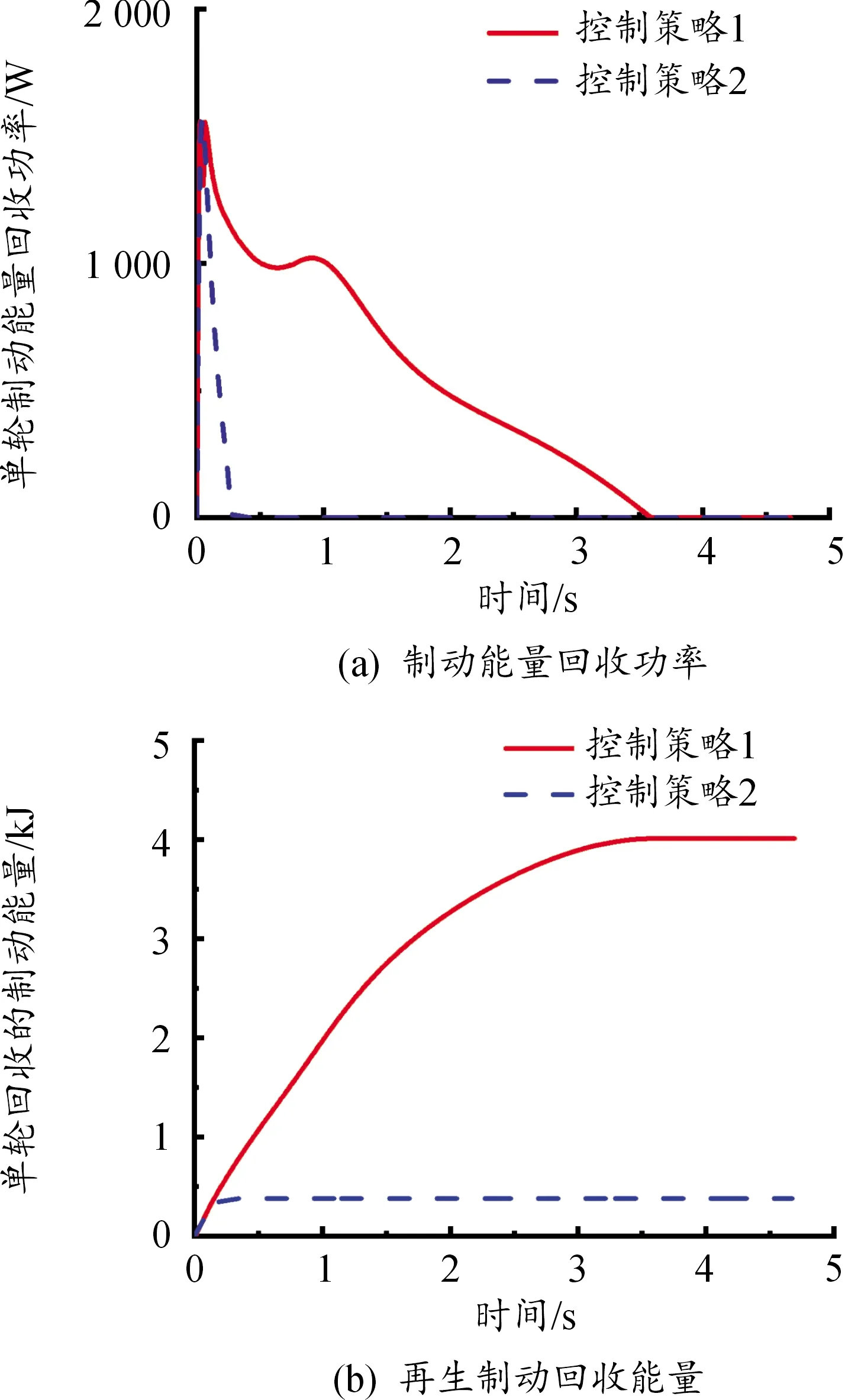
圖9 制動(dòng)工況2下的制動(dòng)能量回收性能隨時(shí)間的變化曲線
2種控制策略下的車輛制動(dòng)時(shí)間和制動(dòng)距離如表4所示。
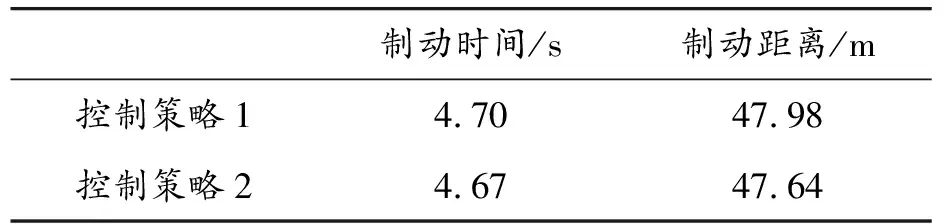
表4 制動(dòng)工況2下的2種控制策略的汽車制動(dòng)性能
由表4可知,采用控制策略1時(shí),汽車制動(dòng)時(shí)間和制動(dòng)距離較大,這是由于在控制策略1中,為了增加制動(dòng)能量回收功率,避免充電電壓過(guò)早降為0,因而減小了總制動(dòng)力矩中再生制動(dòng)力矩的占比,使總制動(dòng)力矩響應(yīng)相較于控制策略2慢,使制動(dòng)時(shí)間與制動(dòng)距離有所增加。
不同制動(dòng)工況下的制動(dòng)能量回收效率如表5所示。
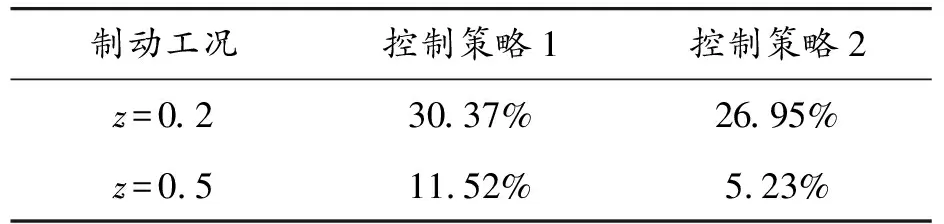
表5 制動(dòng)能量回收效率
綜上所述,本文提出的再生制動(dòng)模糊控制策略在制動(dòng)工況1中,由于再生制動(dòng)占總制動(dòng)力矩比值較大,制動(dòng)時(shí)間和制動(dòng)距離都有所減小,同時(shí),在制動(dòng)工況1中,應(yīng)用本文提出控制策略車輛的制動(dòng)能量回收效率的車輛,相比于應(yīng)用傳統(tǒng)再生制動(dòng)模糊控制策略車輛,其制動(dòng)能量回收效率提高了3.42%。在制動(dòng)工況2中,雖然存在為了增大制動(dòng)能量回收功率,減小了總制動(dòng)力矩中再生制動(dòng)力矩的占比,使其制動(dòng)時(shí)間與制動(dòng)距離變大,但是增加得較小,同時(shí)在制動(dòng)工況2中,其制動(dòng)能量回收效率提高了6.29%。
5 結(jié)論
通過(guò)對(duì)輪轂電機(jī)電動(dòng)車輛再生制動(dòng)能量功率回收最大化的研究,分析了再生制動(dòng)過(guò)程中制動(dòng)能量回收功率和充電電壓之間的關(guān)系,據(jù)此推導(dǎo)出最大制動(dòng)能量回收功率下的制動(dòng)能量回收和再生制動(dòng)力矩的計(jì)算公式;將最大再生制動(dòng)能量回收功率考慮到再生制動(dòng)控制策略中,提出了一種新的再生制動(dòng)模糊控制策略,并據(jù)此設(shè)計(jì)了一種以車速、制動(dòng)強(qiáng)度和最大制動(dòng)能量回收功率下再生制動(dòng)力矩占單輪理想的制動(dòng)力矩的比值為模糊控制的輸入,再生制動(dòng)力矩占總制動(dòng)力矩的比值為輸出的模糊控制器。仿真結(jié)果表明:在輕度制動(dòng)工況下,采用本文提出的控制策略相較于傳統(tǒng)再生制動(dòng)模糊控制策略減少了制動(dòng)距離,其制動(dòng)能量回收效率也提高了3.42%,在中度制動(dòng)工況下,采用本文所提出的控制策略相較于傳統(tǒng)的控制策略雖然使制動(dòng)距離有輕微增加,但是其制動(dòng)能量回收效率提高了6.29%。

